Квантовый хаос

Квантовый хаос — это область физики, пытающаяся соединить теории квантовой механики и классической механики . На рисунке показаны основные идеи, реализуемые в каждом направлении.

Квантовый хаос — это раздел физики , который изучает, как хаотические классические динамические системы могут быть описаны с точки зрения квантовой теории. Главный вопрос, на который пытается ответить квантовый хаос: «Какова связь между квантовой механикой и классическим хаосом ?» Принцип соответствия гласит, что классическая механика является классическим пределом квантовой механики, особенно в пределе, когда отношение постоянной Планка к действию системы стремится к нулю. Если это правда, то в основе классического хаоса должны существовать квантовые механизмы (хотя это может оказаться неэффективным способом изучения классического хаоса). Если квантовая механика не демонстрирует экспоненциальную чувствительность к начальным условиям, то как может возникнуть экспоненциальная чувствительность к начальным условиям в классическом хаосе, который должен быть пределом принципа соответствия квантовой механики?

В поисках решения основного вопроса о квантовом хаосе было использовано несколько подходов:

1. Разработка методов решения квантовых задач, в которых возмущение нельзя считать малым в теории возмущений и где квантовые числа велики.
2. Корреляция статистических описаний собственных значений (уровней энергии) с классическим поведением того же гамильтониана (системы).
3. Исследование распределения вероятностей отдельных собственных состояний (см. Шрамы и Квантовая эргодичность ).
4. Квазиклассические методы, такие как теория периодических орбит, связывающие классические траектории динамической системы с квантовыми особенностями.
5. Прямое применение принципа соответствия.

История

Экспериментальные спектры рекуррентности лития в электрическом поле, показывающие рождение квантовых рекуррентов, соответствующих бифуркациям классических орбит.

В первой половине двадцатого века хаотическое поведение в механике было признано (как и в задаче трёх тел в небесной механике ), но не до конца понято. В этот период были заложены основы современной квантовой механики, по существу оставив в стороне вопрос о квантово-классическом соответствии в системах, классический предел которых демонстрирует хаос.

Подходы

Сравнение экспериментальных и теоретических рекуррентных спектров лития в электрическом поле при приведенной энергии $\epsilon =-3.0$.

Вопросы, связанные с принципом соответствия, возникают во многих различных разделах физики, начиная от , ядерной атомной , молекулярной физики и физики твердого тела и даже до акустики , микроволн и оптики . Однако классико-квантовое соответствие в теории хаоса не всегда возможно. Таким образом, некоторые версии классического эффекта бабочки не имеют аналогов в квантовой механике.

Важными наблюдениями, часто связанными с классически хаотическими квантовыми системами, являются отталкивание спектрального уровня , динамическая локализация во временной эволюции (например, скорость ионизации атомов) и повышенная интенсивность стационарных волн в областях пространства, где классическая динамика демонстрирует только нестабильные траектории (как при рассеянии ). В полуклассическом подходе к квантовому хаосу явления идентифицируются в спектроскопии путем анализа статистического распределения спектральных линий и соединения спектральных периодичностей с классическими орбитами. Другие явления проявляются во временной эволюции квантовой системы или в ее реакции на различные типы внешних сил. В некоторых контекстах, таких как акустика или микроволны, волновые структуры можно наблюдать непосредственно и имеют нерегулярное распределение амплитуд .

Квантовый хаос обычно имеет дело с системами, свойства которых необходимо рассчитывать с использованием либо численных методов, либо схем аппроксимации (см., например, ряды Дайсона ). Простые и точные решения невозможны из-за того, что составляющие системы либо сложным образом влияют друг на друга, либо зависят от изменяющихся во времени внешних сил.

непертурбативных

Рассчитаны регулярные (нехаотические) спектры энергетических уровней ридберговских атомов водорода в электрическом поле вблизи n=15. Обратите внимание, что уровни энергии могут пересекаться из-за лежащей в основе симметрии динамического движения.

Рассчитаны спектры энергетических уровней хаотических ридберговских атомов лития в электрическом поле вблизи n = 15. Обратите внимание, что уровни энергии не могут пересекаться из-за того, что ионное ядро ​​(и возникающий в результате квантовый дефект) нарушает симметрию динамического движения.

Для консервативных систем цель квантовой механики в непертурбативных режимах состоит в том, чтобы найтисобственные значения и собственные векторы гамильтониана вида

$H=H_{s}+\varepsilon H_{ns},\,$

где $H_{s}$ разделима в некоторой системе координат, $H_{ns}$ неразделима в той системе координат, в которой $H_{s}$ отделен, и $\epsilon$ – параметр, который нельзя считать малым. Физики исторически подходили к проблемам такого рода, пытаясь найти систему координат, в которой несепарабельный гамильтониан наименьший, а затем рассматривая несепарабельный гамильтониан как возмущение.

Нахождение констант движения, позволяющих осуществить такое разделение, может оказаться сложной (иногда невозможной) аналитической задачей. Решение классической проблемы может дать ценную информацию о решении квантовой проблемы. Если существуют регулярные классические решенияодин и тот же гамильтониан, то существуют (по крайней мере) приближенные константы движения, и, решив классическую задачу, мы получаем подсказки, как их найти.

В последние годы были разработаны и другие подходы. Один из них состоит в том, чтобы выразить гамильтониан в разные системы координат в разных областях пространства, минимизируя неотделимую часть гамильтониана в каждой области. В этих областях получены волновые функции, а собственные значения получены путем согласования граничных условий.

Другой подход — численная диагонализация матрицы. Если матрица Гамильтона вычисляется в любом полном базисе, собственные значения и собственные векторы получаются путем диагонализации матрица. Однако все полные базисные наборы бесконечны, и нам нужно усечь базис, чтобы получить точные результаты. Эти методы сводятся к выбору усеченной основы, на основе которой можно построить точные волновые функции. Время вычислений, необходимое для диагонализации матрицы, масштабируется как $N^{3}$, где $N$ — размерность матрицы, поэтому важно выбрать наименьший возможный базис, на основе которого можно построить соответствующие волновые функции. Также удобно выбрать базис, в котором матрицаявляется разреженным и/или элементы матрицы задаются простыми алгебраическими выражениями, поскольку вычисление элементов матрицы также может быть трудоемким.

Данный гамильтониан имеет одни и те же константы движения как для классического, так и для квантового. динамика. Квантовые системы также могут иметь дополнительные квантовые числа, соответствующие дискретной симметрии (например, сохранению четности из симметрии отражения). Однако если мы просто найдем квантовые решения гамильтониана, недоступные теории возмущений, мы сможем многое узнать о квантовых решениях, но мало что узнаем о квантовом хаосе. Тем не менее, умение решать такие квантовые проблемы является важной частью ответа на вопрос о квантовом хаосе.

описаний квантовой механики с

Распределение ближайших соседей для спектров энергетических уровней ридберговских атомов в электрическом поле как квантовый дефект увеличено с 0,04 (a) до 0,32 (h). Система становится более хаотичной, поскольку динамическая симметрия нарушается из-за увеличения квантового дефекта; следовательно, распределение развивается от почти распределения Пуассона (а) к распределению, предложенному Вигнером (h).

Статистические меры квантового хаоса возникли из-за желания количественно оценить спектральные характеристики сложных систем. Теория случайных матриц была разработана в попытке охарактеризовать спектры сложных ядер. Замечательный результат состоит в том, что статистические свойства многих систем с неизвестными гамильтонианами можно предсказать, используя случайные матрицы подходящего типа.класс симметрии. Более того, теория случайных матриц также правильно предсказывает статистические свойства.собственных значений многих хаотических систем с известными гамильтонианами. Это делает его полезным в качестве инструмента для характеристики спектров, для расчета которых требуются большие численные усилия.

Для простой количественной оценки спектральных характеристик доступен ряд статистических показателей. Большой интерес представляет вопрос о том, существуют ли универсальные статистические модели поведения классически хаотических систем. Упомянутые здесь статистические тесты универсальны, по крайней мере, для систем с малым количеством степеней свободы ( Берри и Табор выдвинули веские аргументы в пользу распределения Пуассона в случае регулярного движения, а Heusler et al. представляют полуклассическое объяснение так называемой гипотезы Бохигаса–Джаннони–Шмита, утверждающей универсальность спектральных флуктуаций в хаотической динамике). Распределение энергетических уровней ближайших соседей (NND) относительно просто интерпретировать, и оно широко используется для описания квантового хаоса.

Качественные наблюдения отталкивания уровней могут быть оценены количественно и связаны с классической динамикой.с использованием NND, который считается важным признаком классической динамики в квантовых системах. Считается, что регулярная классическая динамика проявляется пуассоновским распределением энергетических уровней:

$P(s)=e^{-s}.\$

Кроме того, ожидается, что системы, которые демонстрируют хаотическое классическое движение, будут характеризоваться статистикой случайных ансамблей собственных значений матрицы. Было показано, что для систем, инвариантных относительно обращения времени, статистика уровня энергии ряда хаотических систем хорошо согласуется с предсказаниями Гауссова ортогонального ансамбля (GOE) случайных матриц, и было высказано предположение, что это явление общий для всех хаотических систем с этой симметрией. Если нормированное расстояние между двумя уровнями энергии равно $s$нормированное распределение расстояний хорошо аппроксимируется выражением

$P(s)={\frac {\pi }{2}}se^{-\pi s^{2}/4}.$

Было обнаружено, что многие гамильтоновы системы, которые являются классически интегрируемыми (нехаотическими), имеют квантовые решения, которые дают распределения ближайших соседей, которые следуют распределениям Пуассона. Точно так же многие системы, демонстрирующие классический хаос, были обнаружены с квантовыми решениями, дающими распределение Вигнера-Дайсона , что подтверждает вышеизложенные идеи. Одним заметным исключением является диамагнитный литий, который, хотя и демонстрирует классический хаос, демонстрирует статистику Вигнера (хаотическую) для уровней энергии с четной четностью и почти пуассоновскую (регулярную) статистику для распределения уровней энергии с нечетной четностью.

Квазиклассические методы

орбиты

Спектр повторяемости четности ( преобразование Фурье плотности состояний ) диамагнитного водорода, показывающий пики, соответствующие периодическим орбитам классической системы. Спектр имеет масштабированную энергию -0,6. Пики, обозначенные R и V, представляют собой повторения замкнутой орбиты, перпендикулярной и параллельной полю соответственно. Пики, отмеченные буквой O, соответствуют почти круговой периодической орбите, вращающейся вокруг ядра.

Относительные амплитуды рекуррентности четных и нечетных рекуррентностей ближней круговой орбиты. Ромбики и знаки плюс обозначают нечетные и четные квартальные периоды соответственно. Сплошная линия — A/cosh(nX/8). Пунктирная линия — A/sinh(nX/8), где A = 14,75 и X = 1,18.

Теория периодических орбит дает рецепт вычисления спектров по периодическим орбитам системы. В отличие от метода квантования действия Эйнштейна-Бриллюэна-Келлера , который применяется только к интегрируемым или почти интегрируемым системам и вычисляет отдельные собственные значения для каждой траектории, теория периодических орбит применима как к интегрируемым, так и к неинтегрируемым системам и утверждает, что каждая периодическая орбита вызывает синусоидальные колебания плотности состояний.

Основным результатом этого развития является выражение для плотности состояний, которое является следом квазиклассической функции Грина и задается формулой следа Гутцвиллера:

$g_{c}(E)=\sum _{k}T_{k}\sum _{n=1}^{\infty }{\frac {1}{2\sinh {(\chi _{nk}/2)}}}\,e^{i(nS_{k}-\alpha _{nk}\pi /2)}.$

Недавно было сделано обобщение этой формулы для произвольных матричных гамильтонианов, которое включает член, подобный фазе Берри, обусловленный спином или другими внутренними степенями свободы. Индекс $k$ различает примитивные периодические орбиты : орбиты с кратчайшим периодом данного набора начальных условий. $T_{k}$ - период примитивной периодической орбиты и $S_{k}$ это его классическое действие. Каждая примитивная орбита возвращается назад, приводя к новой орбите с действием $nS_{k}$ и период, который является целым кратным $n$ первобытного периода. Следовательно, каждое повторение периодической орбиты является другой периодической орбитой. Эти повторы отдельно классифицируются по промежуточной сумме по индексам $n$. $\alpha _{nk}$ орбиты — индекс Маслова .Амплитудный коэффициент, $1/\sinh {(\chi _{nk}/2)}$, представляет собой квадратный корень из плотности соседних орбит. Соседние траектории неустойчивой периодической орбиты экспоненциально расходятся во времени с периодической орбитой. Количество $\chi _{nk}$ характеризует нестабильность орбиты. Устойчивая орбита движется по тору в фазовом пространстве, а вокруг него вьются соседние траектории. Для стабильных орбит $\sinh {(\chi _{nk}/2)}$ становится $\sin {(\chi _{nk}/2)}$, где $\chi _{nk}$ это обмотканомер периодической орбиты. $\chi _{nk}=2\pi m$, где $m$ — это количество раз, когда соседние орбиты пересекают периодическую орбиту за один период. Это представляет трудность, поскольку $\sin {(\chi _{nk}/2)}=0$ в классической бифуркации . Это приводит к тому, что вклад этой орбиты в плотность энергии расходится. Это также происходит в контексте спектра фотопоглощения .

Использование формулы следа для вычисления спектра требует суммирования по всем периодическим орбитам системы. Это представляет несколько трудностей для хаотических систем: 1) Число периодических орбит растет экспоненциально в зависимости от действия. 2) Существует бесконечное число периодических орбит, и свойства сходимости теории периодических орбит неизвестны. Эта трудность также присутствует при применении теории периодических орбит к регулярным системам. 3) Длиннопериодические орбиты трудно вычислить, поскольку большинство траекторий нестабильны и чувствительны к ошибкам округления и деталям численного интегрирования.

Гуцвиллер применил формулу следов для решения анизотропной проблемы Кеплера (одна частица в $1/r$ потенциал с анизотропным тензором массы )полуклассически. Он нашел согласие с квантовыми вычислениями для низколежащих (вплоть до $n=6$) утверждает для небольшой анизотропии, используя только небольшой набор легко вычисляемых периодических орбит, но согласие было плохим для большой анизотропии.

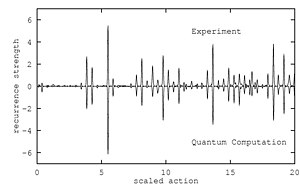
На рисунках выше используется перевернутый подход к проверке теории периодических орбит. Формула следа утверждает, что каждая периодическая орбита вносит в спектр синусоидальный член. Вместо того, чтобы решать вычислительные трудности, связанные с долгопериодическими орбитами, чтобы попытаться найти плотность состояний (уровни энергии), можно использовать стандартную квантово-механическую теорию возмущений для вычисления собственных значений (уровней энергии) и использовать преобразование Фурье для поиска периодических состояний. модуляции спектра, которые являются признаком периодических орбит. Тогда интерпретация спектра сводится к нахождению орбит, соответствующих пикам преобразования Фурье.

того, как прийти к формуле следа

1. Начните с квазиклассического приближения нестационарной функции Грина (пропагатора Ван Флека).
2. Поймите, что для каустик описание расходится, и используйте идеи Маслова (приблизительное преобразование Фурье в пространство импульсов (приближение стационарной фазы с малым параметром), чтобы избежать таких точек и последующее преобразование обратно в пространство позиций, может устранить такое расхождение, однако дает фазу фактор).
3. Преобразуйте функцию Гринса в энергетическое пространство, чтобы получить зависящую от энергии функцию Гринса (снова аппроксимируйте преобразование Фурье с использованием приближения стационарной фазы). Могут появиться новые расхождения, которые необходимо устранить тем же методом, что и в шаге 3.
4. Использовать $d(E)=-{\frac {1}{\pi }}\Im (\operatorname {Tr} (G(x,x^{\prime },E))$ (отслеживание позиций) и снова вычислить его в приближении стационарной фазы, чтобы получить приближение плотности состояний $d(E)$.

Примечание: трассировка показывает, что вклад вносят только замкнутые орбиты, а приближение стационарной фазы каждый раз дает вам ограничительные условия. На шаге 4 вы ограничиваетесь орбитами, у которых начальный и конечный импульс одинаковы, то есть периодическими орбитами. Часто полезно выбрать систему координат, параллельную направлению движения, как это делается во многих книгах.

орбиты

Экспериментальный спектр рекуррентности (кружки) сравнивается с результатами теории замкнутых орбит Джона Делоса и Цзин Гао для ридберговских атомов лития в электрическом поле. Пики, обозначенные цифрами 1–5, представляют собой повторения орбиты электрона, параллельной полю, идущей от ядра к классической точке поворота в направлении вверх.

Теорию замкнутой орбиты разработали Дж. Б. Делос, М. Л. Ду, Дж. Гао и Дж. Шоу. Это похоже натеория периодической орбиты, за исключением того, что теория замкнутой орбиты применима только к атомным и молекулярным спектрам и дает плотность силы осциллятора (наблюдаемый спектр фотопоглощения) из заданного начального состояния, тогда как теория периодической орбиты дает плотность состояний.

В теории замкнутых орбит важны только орбиты, которые начинаются и заканчиваются в ядре. Физически они связаны с исходящими волнами, которые генерируются, когда прочно связанный электрон переводится в высоколежащее состояние. Для ридберговских атомов и молекул каждая орбита, замкнутая в ядре, также является периодической орбитой, период которой равен либо времени замыкания, либо удвоенному времени замыкания.

Согласно теории замкнутой орбиты, средняя плотность силы осциллятора при постоянной $\epsilon$ задается гладким фоном плюс осциллирующая сумма вида

$f(w)=\sum _{k}\sum _{n=1}^{\infty }D_{\it {nk}}^{i}\sin(2\pi nw{\tilde {S_{k}}}-\phi _{\it {nk}}).$

$\phi _{\it {nk}}$ — фаза, которая зависит от индекса Маслова и других деталей орбит. $D_{\it {nk}}^{i}$ - амплитуда повторения замкнутой орбиты для данного начального состояния (обозначенная $i$). Он содержит информацию об устойчивости орбиты, ее начальном и конечном направлениях, а также матричный элемент дипольного оператора между начальным состоянием и кулоновской волной нулевой энергии. Для масштабирующих систем, таких как атомы Ридберга в сильных полях, преобразование Фурье спектра силы осциллятора, вычисленное при фиксированном $\epsilon$ как функция $w$ называется рекуррентным спектром, поскольку он дает пики, соответствующие масштабированному действию замкнутых орбит и высоты которых соответствуют $D_{\it {nk}}^{i}$.

Теория замкнутой орбиты нашла широкое согласие с рядом хаотических систем, включая диамагнитный водород, водород в параллельных электрических и магнитных полях, диамагнитный литий, литий в электрическом поле, $H^{-}$ ион в скрещенных и параллельных электрическом и магнитном полях, барий в электрическом поле и гелий в электрическом поле.

Одномерные системы и потенциал

Для случая одномерной системы с граничным условием $y(0)=0$ плотность состояний, полученная по формуле Гутцвиллера, связана с обратным потенциалу классической системы соотношением ${\frac {d^{1/2}}{dx^{1/2}}}V^{-1}(x)=2{\sqrt {\pi }}{\frac {dN(x)}{dx}}$ здесь ${\frac {dN(x)}{dx}}$ — плотность состояний, а V(x) — классический потенциал частицы, полупроизводная обратного потенциала связана с плотностью состояний, как в потенциале Ву-Спрунга .

Последние направления

Остается открытым вопрос о понимании квантового хаоса в системах, имеющих конечномерные локальные гильбертовы пространства , к которым неприменимы стандартные квазиклассические пределы. Работы последних лет позволили аналитически изучать такие квантовые системы многих тел .

Традиционные темы квантового хаоса касаются спектральной статистики (универсальных и неуниверсальных характеристик) и изучения собственных функций различных хаотических гамильтонианов. Например, до того, как было сообщено о существовании шрамов, предполагалось, что собственные состояния классической хаотической системы равномерно заполняют доступное фазовое пространство, вплоть до случайных флуктуаций и сохранения энергии ( квантовая эргодичность ). Однако собственное квантовое состояние классической хаотической системы может быть повреждено: плотность вероятности собственного состояния увеличивается вблизи периодической орбиты, превышая классическую, статистически ожидаемую плотность вдоль орбиты ( шрамы ). В частности, шрамы являются одновременно ярким визуальным примером классического и квантового соответствия, выходящего за рамки обычного классического предела, и полезным примером квантового подавления хаоса. Например, это очевидно в квантовом рубцевании, вызванном возмущениями: Точнее, в квантовых точках, возмущенных локальными потенциальными выступами (примесями), некоторые собственные состояния сильно повреждены вдоль периодических орбит невозмущенного классического аналога.

Дальнейшие исследования касаются параметрического ( $R$) зависимость гамильтониана, отраженная, например, в статистике предотвращенных пересечений, и связанное с ней перемешивание, отраженное в (параметрической) локальной плотности состояний (LDOS). Существует обширная литература по динамике волновых пакетов, включая изучение флуктуаций, рекуррентностей, вопросов квантовой необратимости и т. д. Особое место отведено изучению динамики квантованных отображений: стандартное отображение и выброшенный ротатор считаются прототипными задачами.

Работы также сосредоточены на изучении управляемых хаотических систем. где гамильтониан $H(x,p;R(t))$ зависит от времени, особенно в адиабатическом и линейном режимах отклика. Также прилагаются значительные усилия по формулированию идей квантового хаоса для сильно взаимодействующих квантовых систем многих тел, далеких от квазиклассических режимов, а также большие усилия по квантовому хаотическому рассеянию.

-

В 1977 году Берри и Тейбор выдвинули все еще открытую «общую» математическую гипотезу, которая, грубо говоря, такова: В «общем» случае квантовой динамики геодезического потока на компактной римановой поверхности собственные значения квантовой энергии ведут себя как последовательность независимых случайных величин при условии, что лежащая в основе классическая динамика полностью интегрируема .

См. также

• Шрам (физика)
• Статистическая механика

Дополнительные ресурсы

• Мартин К. Гуцвиллер (1971). «Периодические орбиты и классические условия квантования». Журнал математической физики . 12 (3): 343–358. Бибкод : 1971JMP....12..343G . дои : 10.1063/1.1665596 .
• Мартин К. Гуцвиллер, Хаос в классической и квантовой механике , (1990) Springer-Verlag , Нью-Йорк ISBN   0-387-97173-4 .
• Ханс-Юрген Штёкманн , Квантовый хаос: Введение , (1999) Издательство Кембриджского университета ISBN   0-521-59284-4 .
• Юджин Пол Вигнер ; Дирак, ПАМ (1951). «О статистическом распределении ширин и расстояний ядерных резонансных уровней». Математические труды Кембриджского философского общества . 47 (4): 790. Бибкод : 1951PCPS...47..790W . дои : 10.1017/S0305004100027237 . S2CID   120852535 .
• Фриц Хааке, Квантовые подписи хаоса, 2-е изд., (2001) Springer-Verlag, Нью-Йорк ISBN   3-540-67723-2 .
• Карл-Фредрик Берггрен и Свен Аберг, «Квантовый хаос Y2K, материалы Нобелевского симпозиума 116» (2001) ISBN   978-981-02-4711-9
• Л. Е. Райхл , «Переход к хаосу: в консервативных классических системах: квантовые проявления», Springer (2004), ISBN   978-0387987880

Внешние ссылки

• Квантовый хаос Мартина Гуцвиллера (1992 и 2008, Scientific American )
• Квантовый хаос Мартина Гуцвиллера Стипендия 2 (12): 3146. doi:10.4249/scholarpedia.3146
• Категория:Наука квантового хаоса
• Что такое... Квантовый хаос ( Зеева Рудника январь 2008 г., Уведомления Американского математического общества )
• Брайан Хейс, «Спектр риманния»; American Scientist Volume 91, номер 4, июль – август 2003 г., стр. 296–300 . Обсуждается связь с дзета-функцией Римана .
• Собственные функции в хаотических квантовых системах Арнда Бекера.
• ChaosBook.org