Ридберговский атом

Рисунок 1: Электронная орбиталь ридберговского атома с n = 12. Цвета показывают квантовую фазу высоковозбужденного электрона.

Рисунок 2: Уровни энергии в атомарном литии , показывающие ряд Ридберга трех самых низких значений орбитального углового момента, сходящихся к первой энергии ионизации.

Атом Ридберга — это возбужденный атом с одним или несколькими электронами которые имеют очень высокое главное квантовое число , n . Чем выше значение n находится электрон от ядра , тем дальше в среднем . Ридберга Атомы обладают рядом специфических свойств, включая чрезмерную реакцию на электрические и магнитные поля . большие периоды распада и электронов волновые функции , которые при некоторых условиях приближаются к классическим орбитам электронов вокруг ядер . Электроны ядра защищают внешний электрон от электрического поля ядра, так что на расстоянии электрический потенциал выглядит идентичным тому, который испытывает электрон в атоме водорода .

Несмотря на свои недостатки, Бора модель атома полезна для объяснения этих свойств. Классически электрон на круговой орбите радиуса r водорода вокруг ядра с зарядом + e подчиняется второму закону Ньютона :

$\mathbf {F} =m\mathbf {a} \Rightarrow {ke^{2} \over r^{2}}={mv^{2} \over r}$

где k = 1/(4π ε ₀ ).

Орбитальный момент квантуется в единицах ħ :

$mvr=n\hbar$.

Объединение этих двух уравнений приводит к Бора для радиуса орбиты через главное квантовое число n выражению :

$r={n^{2}\hbar ^{2} \over ke^{2}m}.$

Теперь понятно, почему ридберговские атомы обладают такими своеобразными свойствами: радиус орбиты масштабируется как n ² ( состояние водорода n = 137 имеет атомный радиус ~1 мкм) и геометрическое сечение как n ⁴ . Таким образом, ридберговские атомы чрезвычайно велики, со слабосвязанными валентными электронами, которые легко возмущаются или ионизируются столкновениями или внешними полями.

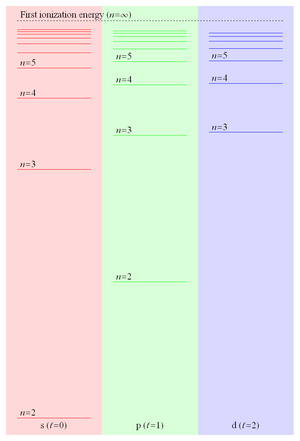
Поскольку энергия связи ридберговского электрона пропорциональна 1/ r и, следовательно, падает как 1/ n ² , расстояние между уровнями энергии падает как 1/ n ³ что приводит к еще более близко расположенным уровням, сходящимся на первой энергии ионизации . Эти близко расположенные состояния Ридберга образуют то, что обычно называют рядом Ридберга . На рис. 2 показаны некоторые энергетические уровни трех нижних значений орбитального момента в литии .

История

Существование ряда Ридберга было впервые продемонстрировано в 1885 году, когда Иоганн Бальмер открыл простую эмпирическую формулу для длин волн света, связанных с переходами в атомарном водороде . Три года спустя шведский физик Йоханнес Ридберг представил обобщенную и более интуитивную версию формулы Бальмера, которая стала известна как формула Ридберга . Эта формула указывала на существование бесконечной серии все более близко расположенных дискретных уровней энергии, сходящихся к конечному пределу.

Этот ряд был качественно объяснен в 1913 году Нильсом Бором с его полуклассической моделью атома водорода, в которой квантованные значения углового момента приводят к наблюдаемым дискретным уровням энергии. Полный количественный вывод наблюдаемого спектра был получен Вольфгангом Паули в 1926 году после развития квантовой механики Вернером Гейзенбергом и другими.

Методы производства

Единственным действительно стабильным состоянием водородоподобного атома является основное состояние с n = 1. Исследование ридберговских состояний требует надежной техники для возбуждения атомов в основном состоянии в состояния с большим значением n .

Возбуждение электронным ударом

Многие ранние экспериментальные работы по ридберговским атомам основывались на использовании коллимированных пучков быстрых электронов, падающих на атомы в основном состоянии. Процессы неупругого рассеяния электронов могут использовать кинетическую энергию для увеличения внутренней энергии атомов, возбуждающей широкий диапазон различных состояний, включая множество высоколежащих ридберговских состояний.

$e^{-}+A\rightarrow A^{*}+e^{-}$.

Поскольку электрон может сохранять любое произвольное количество своей начальной кинетической энергии, этот процесс приводит к образованию популяции с широким разбросом различных энергий.

Возбуждение перезарядкой

Еще одна основа ранних экспериментов с атомами Ридберга основывалась на перезарядке между пучком ионов и популяцией нейтральных атомов другого вида, что приводило к образованию пучка высоковозбужденных атомов.

$A^{+}+B\rightarrow A^{*}+B^{+}$.

Опять же, поскольку кинетическая энергия взаимодействия может вносить вклад в конечную внутреннюю энергию компонентов, этот метод заполняет широкий диапазон энергетических уровней.

Оптическое возбуждение

Появление перестраиваемых лазеров на красителях в 1970-х годах позволило значительно повысить уровень контроля над популяциями возбужденных атомов. При оптическом возбуждении падающий фотон поглощается атомом мишени, что приводит к точному определению энергии конечного состояния. Таким образом, проблема создания моноэнергетических популяций ридберговских атомов в одном состоянии становится несколько более простой проблемой точного управления частотой излучения лазера.

$A+\gamma \rightarrow A^{*}$.

Эта форма прямого оптического возбуждения обычно ограничивается экспериментами с щелочными металлами в основном состоянии , поскольку энергия связи у других видов обычно слишком высока, чтобы быть доступной для большинства лазерных систем.

Для атомов с большой валентного электрона энергией связи (эквивалентной большой первой энергии ионизации ) возбужденные состояния ряда Ридберга недоступны обычным лазерным системам. Первоначальное столкновительное возбуждение может восполнить дефицит энергии, позволяя использовать оптическое возбуждение для выбора конечного состояния. Хотя на начальном этапе происходит возбуждение широкого диапазона промежуточных состояний, точность, присущая процессу оптического возбуждения, означает, что лазерный свет взаимодействует только с определенным подмножеством атомов в определенном состоянии, возбуждая выбранное конечное состояние.

Водородный потенциал

Основная статья: Атом водорода

Рисунок 3 . Сравнение потенциала атома водорода с потенциалом в ридберговском состоянии другого атома. Чтобы сделать эффект более очевидным, была использована большая поляризуемость ядра. Черная кривая представляет собой кулоновский 1/ r- потенциал атома водорода, а пунктирная красная кривая включает 1/ r- потенциал. ⁴ член из-за поляризации ядра иона.

Атом в ридберговском состоянии имеет валентный электрон на большой орбите вдали от ядра иона; на такой орбите самый внешний электрон ощущает почти водородный кулоновский потенциал с UC _ядра от компактного ионного ядра, состоящего из Z протонами и нижних электронных оболочек, заполненных Z -1 электронами. Электрон в сферически-симметричном кулоновском потенциале имеет потенциальную энергию:

$U_{\text{C}}=-{\dfrac {e^{2}}{4\pi \varepsilon _{0}r}}$.

Сходство эффективного потенциала, «видимого» внешним электроном, с водородным потенциалом является определяющей характеристикой ридберговских состояний и объясняет, почему волновые функции электронов приближаются к классическим орбитам в пределе принципа соответствия . Другими словами, орбита электрона напоминает орбиту планет внутри Солнечной системы, подобно тому, что наблюдалось в устаревших, но визуально полезных Бора и Резерфорда моделях атома .

Есть три заметных исключения, которые можно охарактеризовать дополнительным членом, добавленным к потенциальной энергии:

• Атом может иметь два (или более) электрона в высоковозбужденных состояниях с сопоставимыми орбитальными радиусами. В этом случае электрон-электронное взаимодействие приводит к значительному отклонению от водородного потенциала. Для атома в многократном ридберговском состоянии дополнительный член U _ee включает сумму каждой пары высоковозбужденных электронов:

$U_{ee}={\dfrac {e^{2}}{4\pi \varepsilon _{0}}}\sum _{i<j}{\dfrac {1}{|\mathbf {r} _{i}-\mathbf {r} _{j}|}}$.

• Если валентный электрон имеет очень низкий угловой момент (классически интерпретируемый как крайне эксцентричная эллиптическая орбита), то он может пройти достаточно близко, чтобы поляризовать ядро ​​иона, вызывая 1/ r ⁴ Член основной поляризации в потенциале. Взаимодействие между индуцированным диполем и зарядом, который его создает, всегда притягивает, поэтому этот вклад всегда отрицателен.

$U_{\text{pol}}=-{\dfrac {e^{2}\alpha _{\text{d}}}{(4\pi \varepsilon _{0})^{2}r^{4}}}$,

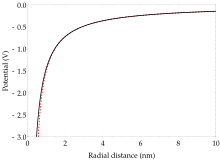
где α _d — дипольная поляризуемость . На рис. 3 показано, как поляризационный член изменяет потенциал вблизи ядра.

• Если внешний электрон проникнет во внутренние электронные оболочки, он «увидит» большую часть заряда ядра и, следовательно, испытает большую силу. В общем, изменение потенциальной энергии рассчитать непросто, и оно должно быть основано на знании геометрии ионного ядра.

Квантово-механические детали

Рисунок 4 . Квазиклассические орбиты для n =5 со всеми разрешенными значениями орбитального момента. Черное пятно обозначает положение атомного ядра.

Квантово-механически состояние с аномально высоким n относится к атому, в котором валентные электроны были возбуждены на ранее незаселенную электронную орбиталь с более высокой энергией и более низкой энергией связи . В водороде энергия связи определяется выражением:

$E_{\text{B}}=-{\frac {\rm {Ry}}{n^{2}}}$,

где Ry = 13,6 эВ — постоянная Ридберга . Низкая энергия связи при высоких значениях n объясняет, почему состояния Ридберга подвержены ионизации.

Дополнительные члены в выражении потенциальной энергии для ридберговского состояния, помимо водородной кулоновской потенциальной энергии, требуют введения квантового дефекта , δ _l , в выражение для энергии связи:

$E_{\text{B}}=-{\frac {\rm {Ry}}{(n-\delta _{l})^{2}}}$.

Электронные

Длительное время жизни ридберговских состояний с высоким орбитальным угловым моментом можно объяснить перекрытием волновых функций. Волновая функция электрона в состоянии с высоким l (высокий угловой момент, «круговая орбита») очень мало перекрывается с волновыми функциями внутренних электронов и, следовательно, остается относительно невозмущенной.

Три исключения из определения ридберговского атома как атома с водородным потенциалом имеют альтернативное квантовомеханическое описание, которое можно охарактеризовать дополнительным членом(ями) в атомном гамильтониане :

• Если второй электрон перевести в состояние n _i , энергетически близкое к состоянию внешнего электрона n _o , то его волновая функция становится почти такой же большой, как у первого (двойное ридберговское состояние). Это происходит, когда n _i приближается к n _o , и приводит к состоянию, когда размеры орбит двух электронов связаны; состояние, которое иногда называют радиальной корреляцией . Член электрон-электронного отталкивания должен быть включен в атомный гамильтониан.
• Поляризация ионного ядра создает анизотропный потенциал, который вызывает угловую корреляцию между движениями двух крайних электронов. Это можно рассматривать как эффект приливной блокировки из-за несферически симметричного потенциала. Член основной поляризации должен быть включен в атомный гамильтониан.
• Волновая функция внешнего электрона в состояниях с низким орбитальным угловым моментом l периодически локализуется внутри оболочек внутренних электронов и взаимодействует с полным зарядом ядра. На рисунке 4 показана полуклассическая интерпретация состояний углового момента на электронной орбитали, иллюстрирующая, что состояния с низким l проходят ближе к ядру, потенциально проникая в ионное ядро. К атомному гамильтониану необходимо добавить член проникновения ядра.

Во внешних полях

Рисунок 5 . Рассчитаны спектры энергетических уровней водорода в электрическом поле вблизи n =15. Потенциальная энергия, найденная в электронном гамильтониане водорода, представляет собой кулоновский потенциал 1/ r (нет квантового дефекта), который не связывает различные штарковские состояния. Следовательно, уровни энергии соседних n- многообразий пересекаются на пределе Инглиса–Теллера.

Рисунок 6 . Рассчитаны спектры энергетических уровней лития в электрическом поле вблизи n =15. Наличие ионного остова, который может быть поляризован и проникнут ридберговским электроном, добавляет дополнительные члены к электронному гамильтониану (что приводит к конечному квантовому дефекту), что приводит к взаимодействию различных штарковских состояний и, следовательно, к предотвращению пересечений энергетических уровней.

Большое расстояние между электроном и ионным остовом в ридберговском атоме делает возможным чрезвычайно большой дипольный момент d электрический . связанная с наличием электрического диполя в электрическом поле Существует энергия , F , известная в атомной физике как штарковский сдвиг .

$E_{\text{S}}=-\mathbf {d} \cdot \mathbf {F} .$

В зависимости от знака проекции дипольного момента на вектор локального электрического поля состояние может иметь энергию, которая увеличивается или уменьшается с увеличением напряженности поля (состояния с низким и высоким полем, ищущие соответственно). Узкое расстояние между соседними n -уровнями в ряду Ридберга означает, что состояния могут приближаться к вырождению даже при относительно небольшой напряженности поля. Теоретическая напряженность поля, при которой произойдет пересечение при условии отсутствия связи между состояниями, определяется пределом Инглиса-Теллера ,

$F_{\text{IT}}={\dfrac {e}{12\pi \varepsilon _{0}a_{0}^{2}n^{5}}}.$

В атоме водорода чистый кулоновский потенциал 1/ r не связывает штарковские состояния из соседних n- многообразий, что приводит к реальным пересечениям, как показано на рисунке 5 . Присутствие дополнительных членов в потенциальной энергии может привести к взаимодействию, в результате которого можно избежать пересечений, как показано для лития на рисунке 6 .

и

захваченных ридберговских

Время жизни радиационного распада атомов из метастабильных состояний в основное состояние важно для понимания астрофизических наблюдений и испытаний стандартной модели.

Исследование диамагнитных эффектов

Большие размеры и низкие энергии связи ридберговских атомов приводят к высокой магнитной восприимчивости . $\chi$. Поскольку диамагнитные эффекты масштабируются пропорционально площади орбиты, а площадь пропорциональна квадрату радиуса ( A ∝ n ⁴ ), эффекты, которые невозможно обнаружить в атомах в основном состоянии, становятся очевидными в ридберговских атомах, которые демонстрируют очень большие диамагнитные сдвиги.

Атомы Ридберга демонстрируют сильную электрическую дипольную связь атомов с электромагнитными полями и используются для обнаружения радиосвязи.

В плазме

Атомы Ридберга обычно образуются в плазме из-за рекомбинации электронов и положительных ионов; рекомбинация с низкой энергией приводит к образованию довольно стабильных ридберговских атомов, тогда как рекомбинация электронов и положительных ионов с высокой кинетической энергией часто образует автоионизирующие ридберговские состояния. Большие размеры ридберговских атомов и их подверженность возмущениям и ионизации электрическими и магнитными полями являются важным фактором, определяющим свойства плазмы.

Конденсация ридберговских атомов образует ридберговскую материю , чаще всего наблюдаемую в виде долгоживущих кластеров. Девозбуждение в ридберговском веществе существенно затруднено обменно-корреляционными эффектами в неоднородной электронной жидкости, образующейся при конденсации коллективными валентными электронами, что приводит к увеличению времени жизни кластеров.

В астрофизике (Линии радиорекомбинации)

Ридберговские атомы возникают в космосе благодаря динамическому равновесию между фотоионизацией горячими звездами и рекомбинацией с электронами, которая при этих очень низких плотностях обычно происходит через повторное присоединение электрона к атому в состоянии с очень высоким n , а затем постепенное снижение энергии уровни в основное состояние, что приводит к возникновению последовательности рекомбинационных спектральных линий, распространяющихся по всему электромагнитному спектру . Очень небольшие различия в энергии между ридберговскими состояниями, отличающимися по n на одну или несколько единиц, означают, что фотоны, излучаемые при переходах между такими состояниями, имеют низкие частоты и длинные волны, вплоть до радиоволн. Впервые такая радиорекомбинационная линия (РРЛ) была обнаружена советскими радиоастрономами в 1964 году; линия, обозначенная H90α, излучалась атомами водорода в состоянии n = 90. Сегодня ридберговские атомы водорода, гелия и углерода в космосе регулярно наблюдаются с помощью РРЛ, наиболее яркими из которых являются линии H n α, соответствующие переходам от n +1 к n. более слабые линии H nβ и H n γ с ∆n Наблюдаются также = 2 и 3. Соответствующие линии для гелия и углерода — He n α, C n α и т. д. Открытие линий с n > 100 было неожиданным, поскольку даже в очень низких плотностях межзвездного пространства, на много порядков ниже, чем в лучших лабораторных вакуумах, достижимых на Земле, ожидалось, что такие высоковозбужденные атомы будут часто разрушаться. из-за столкновений, что делает линии ненаблюдаемыми. Усовершенствованный теоретический анализ показал, что этот эффект был переоценен, хотя столкновительное уширение в конечном итоге ограничивает возможность обнаружения линий при очень высоких n . Рекордная длина волны для водорода составляет λ = 73 см для H253α, что подразумевает диаметр атомов в несколько микрон, а для углерода λ = 18 метров для C732α, из атомов диаметром 57 микрон.

RRL из водорода и гелия производятся в сильно ионизированных областях ( области H II и теплая ионизированная среда ). Углерод имеет более низкую энергию ионизации , чем водород, поэтому однократно ионизированные атомы углерода и соответствующие рекомбинирующие ридберговские состояния существуют дальше от ионизирующих звезд, в так называемых областях C II, которые образуют толстые оболочки вокруг областей H II. Больший объем частично компенсирует низкое содержание C по сравнению с H, что делает углеродные RRL обнаруживаемыми.

В отсутствие столкновительного уширения длины волн RRL изменяются только за счет эффекта Доплера , поэтому измеренная длина волны $\lambda$, обычно преобразуется в радиальную скорость, $v\approx c(\lambda -\lambda _{0})/\lambda _{0}$, где $\lambda _{0}$ – длина волны покоящегося кадра . Области H II в нашей Галактике могут иметь лучевые скорости до ± 150 км/с из-за их движения относительно Земли, когда обе они вращаются вокруг центра Галактики. Эти движения настолько регулярны, что $v$ может использоваться для оценки положения области H II на луче зрения и, следовательно, ее трехмерного положения в Галактике. Поскольку все астрофизические ридберговские атомы являются водородными , частоты переходов для H, He и C задаются одной и той же формулой , за исключением немного различной приведенной массы валентного электрона для каждого элемента. Это дает видимые доплеровские сдвиги линий гелия и углерода на -100 и -140 км/с соответственно относительно соответствующей линии водорода.

РРЛ используются для обнаружения ионизированного газа в отдаленных регионах нашей Галактики, а также во внешних галактиках , поскольку радиофотоны не поглощаются межзвездной пылью , которая блокирует фотоны от более привычных оптических переходов. температуры ионизированного газа через отношение интенсивности линии к непрерывному тормозному излучению плазмы Они также используются для измерения . Поскольку температура областей H II регулируется излучением линий более тяжелых элементов, таких как C, N и O, рекомбинационные линии также косвенно измеряют их содержание ( металличность ).

RRL разбросаны по всему радиоспектру с относительно небольшими интервалами длины волны между ними, поэтому они часто встречаются при радиоспектральных наблюдениях, направленных в первую очередь на другие спектральные линии. Например, H166α, H167α и H168α по длине волны очень близки к линии 21 см нейтрального водорода. Это позволяет радиоастрономам изучать как нейтральную, так и ионизованную межзвездную среду на основе одной и той же серии наблюдений. Поскольку RRL многочисленны и слабы, обычной практикой является усреднение спектров скоростей нескольких соседних линий для повышения чувствительности.

Существует множество других потенциальных применений ридберговских атомов в космологии и астрофизике.

Сильно взаимодействующие системы

Из-за своего большого размера атомы Ридберга могут проявлять очень большие электрические дипольные моменты . Расчеты с использованием теории возмущений показывают, что это приводит к сильным взаимодействиям между двумя близкими ридберговскими атомами. Когерентный контроль этих взаимодействий в сочетании с их относительно длительным временем жизни делает их подходящим кандидатом для реализации квантового компьютера . В 2010 году экспериментально были созданы двухкубитные вентили . Сильно взаимодействующие ридберговские атомы также обладают квантово-критическим поведением, что делает их интересными для самостоятельного изучения.

исследований

С 2000-х годов исследования атомов Ридберга охватывают пять направлений: зондирование, квантовая оптика , квантовые вычисления, квантовое моделирование и квантовые вопросы. Высокие электрические дипольные моменты между атомными состояниями Ридберга используются для радиочастотного и терагерцового зондирования и визуализации. включая без разрушения . измерения отдельных микроволновых фотонов Электромагнитно-индуцированная прозрачность использовалась в сочетании с сильными взаимодействиями между двумя атомами, возбужденными в состоянии Ридберга, чтобы создать среду, которая демонстрирует сильно нелинейное поведение на уровне отдельных оптических фотонов. Настраиваемое взаимодействие между состояниями Ридберга позволило также провести первые эксперименты по квантовому моделированию.

В октябре 2018 года Исследовательская лаборатория армии США публично обсудила усилия по разработке сверхширокополосного радиоприемника с использованием ридберговских атомов. В марте 2020 года лаборатория объявила, что ее ученые проанализировали чувствительность датчика Ридберга к осциллирующим электрическим полям в огромном диапазоне частот — от 0 до 10. ¹² Герца (спектр до длины волны 0,3 мм). Датчик Ридберга может надежно обнаруживать сигналы во всем спектре и выгодно отличаться от других известных технологий датчиков электрического поля, таких как электрооптические кристаллы и пассивная электроника с дипольной антенной.

Классическое моделирование

Рисунок 7 . Потенциал Штарка – Кулона для ридберговского атома в статическом электрическом поле. Электрон в таком потенциале испытывает крутящий момент, способный изменить его угловой момент.

Рисунок 8 . Траектория электрона в атоме водорода в электрическом поле Е = -3 х 10 ⁶ В/м в направлении x . Обратите внимание, что классически разрешены все значения углового момента; На рисунке 4 показаны конкретные орбиты, связанные с квантово-механически разрешенными значениями. Посмотрите анимацию .

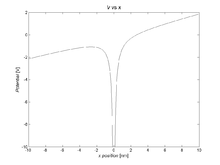
Простой потенциал 1/ r приводит к замкнутой кеплеровской эллиптической орбите . В присутствии внешнего электрического поля атомы Ридберга могут получить очень большие электрические дипольные моменты, что делает их чрезвычайно восприимчивыми к возмущениям поля. На рисунке 7 показано, как приложение внешнего электрического поля (известного в атомной физике как поле Штарка ) меняет геометрию потенциала, кардинально меняя поведение электрона. Кулоновский потенциал не создает никакого крутящего момента , поскольку сила всегда антипараллельна вектору положения (всегда направленному вдоль линии, проходящей между электроном и ядром):

$|\mathbf {\tau } |=|\mathbf {r} \times \mathbf {F} |=|\mathbf {r} ||\mathbf {F} |\sin \theta$,

$\theta =\pi \Rightarrow \mathbf {\tau } =0$.

При приложении статического электрического поля электрон ощущает постоянно меняющийся крутящий момент. Результирующая траектория со временем становится все более искажённой, в конечном итоге проходя полный диапазон углового момента от L = L _MAX до прямой линии L =0 и до начальной орбиты в противоположном направлении. L = - L _МАКС .

Период времени колебания углового момента (время завершения траектории на рисунке 8 ) почти точно соответствует квантовомеханически предсказанному периоду возврата волновой функции в исходное состояние, демонстрируя классическую природу ридберговского атома.

См. также

• Тяжелая система Ридберга
• Старая квантовая теория
• Квантовый хаос
• Молекула Ридберга
• Ридбергский полярон