поляризуемость

Поляризуемость обычно относится к тенденции вещества под воздействием электрического поля приобретать электрический дипольный момент, пропорциональный приложенному полю. Это свойство частиц с электрическим зарядом . Под действием электрического поля отрицательно заряженные электроны и положительно заряженные атомные ядра подвергаются действию противоположных сил и подвергаются разделению зарядов . материала Поляризуемость отвечает за диэлектрическую проницаемость и, на высоких (оптических) частотах, за его показатель преломления .

Поляризуемость атома или молекулы определяется как отношение его индуцированного дипольного момента к локальному электрическому полю; в кристаллическом твердом теле учитывают дипольный момент на элементарную ячейку . ^[1] Обратите внимание, что локальное электрическое поле, видимое молекулой, обычно отличается от макроскопического электрического поля, которое можно было бы измерить извне. Это несоответствие учитывается соотношением Клаузиуса – Моссотти (ниже), которое связывает объемное поведение ( плотность поляризации из-за внешнего электрического поля в соответствии с электрической восприимчивостью $\chi =\varepsilon _{\mathrm {r} }-1$ ) с молекулярной поляризуемостью $\alpha$ из-за местного поля.

Магнитная поляризуемость также относится к тенденции появления магнитного дипольного момента пропорционально внешнему магнитному полю . Электрическая и магнитная поляризуемость определяют динамический отклик связанной системы (например, молекулы или кристалла) на внешние поля и позволяют понять внутреннюю структуру молекулы. ^[2] «Поляризуемость» не следует путать с собственным магнитным или электрическим дипольным моментом атома, молекулы или объемного вещества; они не зависят от наличия внешнего поля.

Электрическая поляризуемость

Определение

Электрическая поляризуемость — это относительная тенденция распределения заряда, такого как облако атома молекулы или электронное , искажаться от его нормальной формы под действием внешнего электрического поля .

Поляризуемость $\alpha$ в изотропных средах определяется как отношение индуцированного дипольного момента $\mathbf {p}$ атома в электрическое поле $\mathbf {E}$ который создает этот дипольный момент. ^[3]

\alpha ={\frac {|\mathbf {p} |}{|\mathbf {E} |}}

Поляризуемость имеет единицы СИ См·м. ²·V ⁻¹ = А ²·с ⁴·кг ⁻¹ в то время как его единица измерения cgs - см ³. Обычно его выражают в единицах СГС как так называемый объем поляризуемости, иногда выражаемый в Å. ³ = 10 ⁻²⁴ см ³. Можно конвертировать из единиц СИ ( $\alpha$ ) в единицы СГС ( $\alpha '$ ) следующее:

\alpha '(\mathrm {cm} ^{3})={\frac {10^{6}}{4\pi \varepsilon _{0}}}\alpha (\mathrm {C{\cdot }m^{2}{\cdot }V^{-1}} )={\frac {10^{6}}{4\pi \varepsilon _{0}}}\alpha (\mathrm {F{\cdot }m^{2}} )

≃ 8.988×10 ¹⁵ ×

\alpha (\mathrm {F{\cdot }m^{2}} )

где $\varepsilon _{0}$ , вакуумная диэлектрическая проницаемость составляет ~8,854 × 10 ⁻¹² (Ж/м). Если обозначить объем поляризуемости в единицах СГС $\alpha '$ отношение может быть выражено в общем виде ^[4] (в системе СИ) как $\alpha =4\pi \varepsilon _{0}\alpha '$ .

Поляризуемость отдельных частиц связана со средней электрической восприимчивостью среды соотношением Клаузиуса–Моссотти :

R={\displaystyle \left({\frac {4\pi }{3}}\right)N_{\text{A}}\alpha _{c}=\left({\frac {M}{p}}\right)\left({\frac {\varepsilon _{\mathrm {r} }-1}{\varepsilon _{\mathrm {r} }+2}}\right)}

где R — молярная рефракция , $N_{\text{A}}$ – постоянная Авогадро , $\alpha _{c}$ – электронная поляризуемость, p – плотность молекул, M – молярная масса , $\varepsilon _{\mathrm {r} }=\epsilon /\epsilon _{0}$ материала — относительная диэлектрическая проницаемость или диэлектрическая проницаемость (или в оптике квадрат показателя преломления ).

Поляризуемость анизотропных или несферических сред, вообще говоря, не может быть представлена как скалярная величина. Определение $\alpha$ в качестве скаляра подразумевает, что приложенные электрические поля могут индуцировать только компоненты поляризации, параллельные полю, и что $x,y$ и $z$ направления одинаково реагируют на приложенное электрическое поле. Например, электрическое поле в $x$ -направление может производить только $x$ компонент в $\mathbf {p}$ и если бы то же самое электрическое поле было приложено в $y$ -направлении индуцированная поляризация будет такой же по величине, но появится в $y$ компонент $\mathbf {p}$ . Многие кристаллические материалы имеют направления, которые легче поляризовать, чем другие, а некоторые даже поляризуются в направлениях, перпендикулярных приложенному электрическому полю. ^{[ нужна ссылка ]}, и то же самое происходит с несферическими телами. Некоторые молекулы и материалы с такой анизотропией являются оптически активными или демонстрируют линейное двойное лучепреломление света.

Тензор

поляризуемости второго ранга Для описания анизотропных сред используется тензор или $3\times 3$ матрица $\alpha$ определяется,

\mathbb {\alpha } ={\begin{bmatrix}\alpha _{xx}&\alpha _{xy}&\alpha _{xz}\\\alpha _{yx}&\alpha _{yy}&\alpha _{yz}\\\alpha _{zx}&\alpha _{zy}&\alpha _{zz}\\\end{bmatrix}}

так что:

\mathbf {p} =\mathbb {\alpha } \mathbf {E}

Элементами, описывающими отклик, параллельный приложенному электрическому полю, являются элементы, расположенные по диагонали. Большое значение $\alpha _{yx}$ здесь означает, что электрическое поле, приложенное в $x$ -направление сильно поляризует материал в $y$ -направление. Явные выражения для $\alpha$ даны для однородных анизотропных эллипсоидальных тел. ^[5]^[6]

Применение в кристаллографии

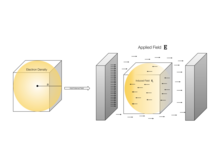
Приведенную выше матрицу можно использовать с уравнением молярной рефракции и другими данными для получения данных о плотности для кристаллографии. Каждое измерение поляризуемости вместе с показателем преломления, связанным с его направлением, дает плотность конкретного направления, которую можно использовать для точной трехмерной оценки молекулярной упаковки в кристалле. Эту взаимосвязь впервые заметил Лайнус Полинг . ^[1]

Поляризуемость и молекулярные свойства связаны с показателем преломления и объемными свойствами. В кристаллических структурах взаимодействия между молекулами рассматриваются путем сравнения локального поля с макроскопическим полем. Анализируя кубическую кристаллическую решетку , мы можем представить изотропную сферическую область, представляющую весь образец. Придание региону радиуса $a$ , поле будет равно объему сферы, умноженному на дипольный момент на единицу объема. $\mathbf {P} .$

\mathbf {p}

=

{\frac {4\pi a^{3}}{3}}

\mathbf {P} .

Мы можем позвонить в наше местное поле $\mathbf {F}$ , наше макроскопическое поле $\mathbf {E}$ , и поле, создаваемое материей внутри сферы, $\mathbf {E} _{\mathrm {in} }={\tfrac {-\mathbf {P} }{3\varepsilon _{0}}}$ ^[7] Тогда мы можем определить локальное поле как макроскопическое поле без вклада внутреннего поля:

\mathbf {F} =\mathbf {E} -\mathbf {E} _{\mathrm {in} }=\mathbf {E} +{\frac {\mathbf {P} }{3\varepsilon _{0}}}

Поляризация пропорциональна макроскопическому полю соотношением $\mathbf {P} =\varepsilon _{0}(\varepsilon _{r}-1)\mathbf {E} =\chi _{\text{e}}\varepsilon _{0}\mathbf {E}$ где $\varepsilon _{0}$ - постоянная электрической проницаемости и $\chi _{\text{e}}$ это электрическая восприимчивость . Используя эту пропорциональность, мы находим локальное поле как $\mathbf {F} ={\tfrac {1}{3}}(\varepsilon _{\mathrm {r} }+2)\mathbf {E}$ который можно использовать при определении поляризации

\mathbf {P} ={\frac {N\alpha }{V}}\mathbf {F} ={\frac {N\alpha }{3V}}(\varepsilon _{\mathrm {r} }+2)\mathbf {E}

и упрощено с помощью $\varepsilon _{\mathrm {r} }=1+{\tfrac {N\alpha }{\varepsilon _{0}V}}$ получить $\mathbf {P} =\varepsilon _{0}(\varepsilon _{\mathrm {r} }-1)\mathbf {E}$ . Оба этих термина можно приравнять к другому, устраняя необходимость $\mathbf {E}$ срок, дающий нам

{\frac {\varepsilon _{\mathrm {r} }-1}{\varepsilon _{\mathrm {r} }+2}}={\frac {N\alpha }{3\varepsilon _{0}V}}

.

Мы можем заменить относительную диэлектрическую проницаемость $\varepsilon _{\mathrm {r} }$ с показателем преломления $n$ , с $\varepsilon _{\mathrm {r} }=n^{2}$ для газа низкого давления. Численная плотность может быть связана с молекулярной массой. $M$ и массовая плотность $\rho$ через ${\tfrac {N}{V}}={\tfrac {N_{\mathrm {A} }\rho }{M}}$ , корректируя окончательную форму нашего уравнения, включив в него молярную рефракцию:

R_{\mathrm {M} }={\frac {N_{\mathrm {A} }\alpha }{3\varepsilon _{0}}}=\left({\frac {M}{\rho }}\right){\frac {n^{2}-1}{n^{2}+2}}

Это уравнение позволяет нам связать объемное свойство ( показатель преломления ) с молекулярным свойством (поляризуемость) как функцию частоты. ^[8]

Тенденции

Обычно поляризуемость увеличивается с увеличением объема, занимаемого электронами. ^[9] В атомах это происходит потому, что более крупные атомы имеют более свободно удерживаемые электроны в отличие от меньших атомов с прочно связанными электронами. ^[9]^[10] Поэтому в строках таблицы Менделеева поляризуемость уменьшается слева направо. ^[9] Поляризуемость увеличивается вниз по столбцам таблицы Менделеева. ^[9] Аналогичным образом, более крупные молекулы обычно более поляризуемы, чем более мелкие.

Вода — очень полярная молекула, но алканы и другие гидрофобные молекулы более поляризуемы. Вода с ее постоянным диполем с меньшей вероятностью изменит форму под действием внешнего электрического поля. Алканы являются наиболее поляризуемыми молекулами. ^[9] Хотя ожидается, что алкены и арены будут иметь большую поляризуемость, чем алканы, из-за их более высокой реакционной способности по сравнению с алканами, на самом деле алканы более поляризуемы. ^[9] Это происходит из-за более электроотрицательных sp алкенов и аренов. ² углерода к менее электроотрицательному sp алкана ³ углероды. ^[9]

Модели электронной конфигурации основного состояния часто неадекватны для изучения поляризуемости связей, поскольку в ходе реакции происходят резкие изменения в молекулярной структуре. ^{[ нужны разъяснения ]}^[9]

Магнитная поляризуемость

Магнитная поляризуемость, определяемая спиновыми взаимодействиями нуклонов, является важным параметром дейтронов и адронов . В частности, измерение тензорной поляризуемости нуклонов дает важную информацию о спин-зависимых ядерных силах. ^[11]

Метод спиновых амплитуд использует формализм квантовой механики для более простого описания спиновой динамики. Векторная и тензорная поляризация частиц/ядер со спином $S \geq 1$ задается единичным вектором поляризации. $\mathbf {p}$ и тензор поляризации P _` . Дополнительные тензоры, состоящие из произведений трех и более спиновых матриц, нужны только для исчерпывающего описания поляризации частиц/ядер со спином $S ≥ .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}3 ⁄ 2$ . ^[11]

См. также

Диэлектрик
Электрическая восприимчивость
Плотность поляризации
MOSCED — метод оценки коэффициентов активности , в котором поляризуемость используется в качестве одного из параметров.

Ссылки

^ Jump up to: ^а ^б Лиде, Дэвид (1998). Справочник CRC по химии и физике . Издательство химической резины. стр. 12–17.
^ Л. Чжоу; FX Ли; В. Уилкокс; Дж. Кристенсен (2002). «Магнитная поляризуемость адронных частиц из решетки КХД» (PDF) . Европейская организация ядерных исследований ( ЦЕРН ) . Проверено 25 мая 2010 г.
^ Введение в электродинамику (3-е издание), DJ Гриффитс, Pearson Education, Дорлинг Киндерсли, 2007, ISBN 81-7758-293-3
^ Аткинс, Питер; де Паула, Хулио (2010). «17». Физическая химия Аткинса . Издательство Оксфордского университета . стр. 622–629. ISBN 978-0-19-954337-3 .
^ Электродинамика сплошных сред, Л.Д. Ландау и Э.М. Лифшиц, Pergamon Press, 1960, стр. 7 и 192.
^ CE Соливерес, Электростатика и магнитостатика поляризованных эллипсоидальных тел: метод тензора деполяризации , Бесплатная научная информация, 2016 (2-е издание), ISBN 978-987-28304-0-3 , стр. 20, 23, 32, 30, 33, 114 и 133.
^ 1. Дж. Д. Джексон, Классическая электродинамика (Уайли, Нью-Йорк, 1962).
^ Макхейл, JL (2017). Молекулярная спектроскопия (2-е изд.). ЦРК Пресс.
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час Анслин, Эрик; Догерти, Деннис (2006). Современная физико-органическая химия . Университетская наука. ISBN 978-1-891389-31-3 . [1]
^ Швердтфегер, Питер (2006). «Вычислительные аспекты расчета электрической поляризуемости: атомы, молекулы и кластеры». В Г. Марулисе (ред.). Атомные статические дипольные поляризуемости . IOS Пресс . [2] ^{[ постоянная мертвая ссылка ]}
^ Jump up to: ^а ^б А.Я. Силенко (18 ноября 2008 г.). «Проявление тензорной магнитной поляризуемости дейтрона в экспериментах с накопителем». Специальные темы Европейского физического журнала . 162 (1). Шпрингер Берлин / Гейдельберг: 59–62. Бибкод : 2008EPJST.162...59S . дои : 10.1140/epjst/e2008-00776-9 . S2CID 122690288 .

[:0-1] Jump up to: ^а ^б Лиде, Дэвид (1998). Справочник CRC по химии и физике . Издательство химической резины. стр. 12–17.

[CERN-2] Л. Чжоу; FX Ли; В. Уилкокс; Дж. Кристенсен (2002). «Магнитная поляризуемость адронных частиц из решетки КХД» (PDF) . Европейская организация ядерных исследований ( ЦЕРН ) . Проверено 25 мая 2010 г.

[3] Введение в электродинамику (3-е издание), DJ Гриффитс, Pearson Education, Дорлинг Киндерсли, 2007, ISBN 81-7758-293-3

[Atkins-4] Аткинс, Питер; де Паула, Хулио (2010). «17». Физическая химия Аткинса . Издательство Оксфордского университета . стр. 622–629. ISBN 978-0-19-954337-3 .

[5] Электродинамика сплошных сред, Л.Д. Ландау и Э.М. Лифшиц, Pergamon Press, 1960, стр. 7 и 192.

[6] CE Соливерес, Электростатика и магнитостатика поляризованных эллипсоидальных тел: метод тензора деполяризации , Бесплатная научная информация, 2016 (2-е издание), ISBN 978-987-28304-0-3 , стр. 20, 23, 32, 30, 33, 114 и 133.

[7] 1. Дж. Д. Джексон, Классическая электродинамика (Уайли, Нью-Йорк, 1962).

[8] Макхейл, JL (2017). Молекулярная спектроскопия (2-е изд.). ЦРК Пресс.

[anslyn-9] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час Анслин, Эрик; Догерти, Деннис (2006). Современная физико-органическая химия . Университетская наука. ISBN 978-1-891389-31-3 . [1]

[Schwerdtfeger-10] Швердтфегер, Питер (2006). «Вычислительные аспекты расчета электрической поляризуемости: атомы, молекулы и кластеры». В Г. Марулисе (ред.). Атомные статические дипольные поляризуемости . IOS Пресс . [2] ^{[ постоянная мертвая ссылка ]}

[Silenko-11] Jump up to: ^а ^б А.Я. Силенко (18 ноября 2008 г.). «Проявление тензорной магнитной поляризуемости дейтрона в экспериментах с накопителем». Специальные темы Европейского физического журнала . 162 (1). Шпрингер Берлин / Гейдельберг: 59–62. Бибкод : 2008EPJST.162...59S . дои : 10.1140/epjst/e2008-00776-9 . S2CID 122690288 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]