Магнитный диполь

Магнитное поле, создаваемое естественными магнитными диполями (вверху слева), магнитными монополями (вверху справа), электрическим током в круговой петле (внизу слева) или в соленоиде (внизу справа). Все они генерируют одинаковый профиль поля, когда расположение бесконечно мало.

В электромагнетизме магнитный диполь является пределом либо замкнутого контура электрического тока , либо пары полюсов, поскольку размер источника уменьшается до нуля при сохранении постоянного магнитного момента .

Это магнитный аналог электрического диполя , но аналогия не идеальна. настоящий магнитный монополь — магнитный аналог электрического заряда В частности, в природе никогда не наблюдался . Однако магнитные монопольные квазичастицы наблюдались как новые свойства некоторых систем конденсированного вещества. Более того, одна из форм магнитного дипольного момента связана с фундаментальным квантовым свойством — спином элементарных частиц .

Поскольку магнитных монополей не существует, магнитное поле на большом расстоянии от любого статического магнитного источника выглядит как поле диполя с тем же дипольным моментом. Для источников более высокого порядка (например, квадруполей ) без дипольного момента их поле затухает к нулю с расстоянием быстрее, чем дипольное поле.

моментом

Электростатический аналог магнитного момента: два противоположных заряда, разделенные конечным расстоянием. Каждая стрелка представляет направление вектора поля в этой точке.

Магнитное поле токовой петли. Кольцо представляет текущий цикл, который входит в страницу в точке x и выходит в точке.

В классической физике магнитное поле диполя рассчитывается как предел либо токовой петли, либо пары зарядов, когда источник сжимается до точки, сохраняя при этом магнитный момент m постоянным. Для токового контура этот предел легче всего получить из векторного потенциала :

${\mathbf {A} }({\mathbf {r} })={\frac {\mu _{0}}{4\pi r^{2}}}{\frac {{\mathbf {m} }\times {\mathbf {r} }}{r}}={\frac {\mu _{0}}{4\pi }}{\frac {{\mathbf {m} }\times {\mathbf {r} }}{r^{3}}},$

где µ ₀ — константа вакуумной проницаемости и 4 π r ² — поверхность сферы радиуса r .Тогда плотность магнитного потока (сила B-поля) равна

$\mathbf {B} ({\mathbf {r} })=\nabla \times {\mathbf {A} }={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {r} (\mathbf {m} \cdot \mathbf {r} )}{r^{5}}}-{\frac {\mathbf {m} }{r^{3}}}\right].$

В качестве альтернативы можно сначала получить скалярный потенциал из предела магнитного полюса:

$\psi ({\mathbf {r} })={\frac {{\mathbf {m} }\cdot {\mathbf {r} }}{4\pi r^{3}}},$

и, следовательно, напряженность магнитного поля (или напряженность H-поля) равна

${\mathbf {H} }({\mathbf {r} })=-\nabla \psi ={\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {m} \cdot \mathbf {\hat {r}} )-\mathbf {m} }{r^{3}}}\right]={\frac {\mathbf {B} }{\mu _{0}}}.$

Напряженность магнитного поля симметрична относительно вращений вокруг оси магнитного момента.В сферических координатах, с $\mathbf {\hat {z}} =\mathbf {\hat {r}} \cos \theta -{\boldsymbol {\hat {\theta }}}\sin \theta$, а магнитный момент ориентирован по оси z, тогда напряженность поля проще выразить как

$\mathbf {H} ({\mathbf {r} })={\frac {|\mathbf {m} |}{4\pi r^{3}}}\left(2\cos \theta \,\mathbf {\hat {r}} +\sin \theta \,{\boldsymbol {\hat {\theta }}}\right).$

Внутреннее магнитное поле диполя

См. Также: Магнитный момент § Определение магнитного полюса.

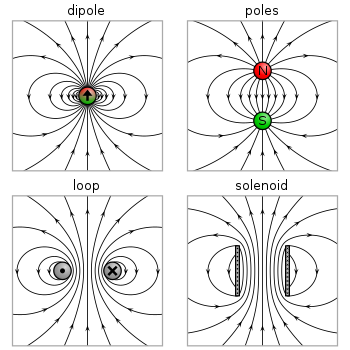
Две модели диполя (токовая петля и магнитные полюса) дают одинаковые предсказания для магнитного поля вдали от источника. Однако внутри исходного региона они дают разные прогнозы. Магнитное поле между полюсами направлено противоположно магнитному моменту (который направлен от отрицательного заряда к положительному заряду), а внутри токовой петли оно направлено в том же направлении (см. рисунок справа (выше для мобильных пользователей). )). Очевидно, что пределы этих полей также должны быть разными, поскольку источники уменьшаются до нулевого размера. Это различие имеет значение только в том случае, если дипольный предел используется для расчета полей внутри магнитного материала.

Если магнитный диполь формируется путем уменьшения и уменьшения токовой петли, но при сохранении постоянного произведения тока на площадь, ограничивающее поле будет равно

$\mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}+{\frac {8\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right],$

где δ ( r ) — дельта-функция Дирака в трех измерениях. В отличие от выражений предыдущего раздела, этот предел справедлив для внутреннего поля диполя.

Если магнитный диполь формируется путем взятия «северного полюса» и «южного полюса», сближения их все ближе и ближе, но сохранения произведения заряда магнитного полюса и расстояния постоянным, предельное поле будет равно

$\mathbf {H} (\mathbf {r} )={\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}-{\frac {4\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right].$

Эти поля связаны соотношением B = µ ₀ ( H + M ) , где

$\mathbf {M} (\mathbf {r} )=\mathbf {m} \delta (\mathbf {r} )$

это намагниченность .

между двумя

Смотрите также: Сила между магнитами § Магнитное диполь-дипольное взаимодействие

Силу F , действующую со стороны одного дипольного момента m ₁ на другой m _{2 ,} разделенный в пространстве вектором r, можно рассчитать с помощью:

$\mathbf {F} =\nabla \left(\mathbf {m} _{2}\cdot \mathbf {B} _{1}\right),$

или

$\mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\dfrac {3\mu _{0}}{4\pi r^{5}}}\left[(\mathbf {m} _{1}\cdot \mathbf {r} )\mathbf {m} _{2}+(\mathbf {m} _{2}\cdot \mathbf {r} )\mathbf {m} _{1}+(\mathbf {m} _{1}\cdot \mathbf {m} _{2})\mathbf {r} -{\dfrac {5(\mathbf {m} _{1}\cdot \mathbf {r} )(\mathbf {m} _{2}\cdot \mathbf {r} )}{r^{2}}}\mathbf {r} \right],$

где r — расстояние между диполями. Сила, действующая на m _1, направлена ​​в противоположном направлении.

Крутящий момент можно найти по формуле

${\boldsymbol {\tau }}=\mathbf {m} _{2}\times \mathbf {B} _{1}.$

поля от

См. Также: Ближнее и дальнее поле.

Магнитный скалярный потенциал ψ, создаваемый конечным источником, но внешним по отношению к нему, может быть представлен мультипольным разложением . Каждому члену разложения соответствует характерный момент и потенциал, имеющий характерную скорость убывания с расстоянием r от источника. Монопольные моменты имеют 1/ r скорость убывания , дипольные моменты имеют скорость 1/ r. ² скорость, квадрупольные моменты имеют 1/ r ³ ставка и так далее. Чем выше порядок, тем быстрее падает потенциал. Поскольку самым низким членом, наблюдаемым в магнитных источниках, является дипольный член, он доминирует на больших расстояниях. Поэтому на больших расстояниях любой магнитный источник выглядит как диполь с одинаковым магнитным моментом .

Ссылки

• Чоу, Тай Л. (2006). Введение в теорию электромагнетизма: современный взгляд . Джонс и Бартлетт Обучение . ISBN  978-0-7637-3827-3 .
• Джексон, Джон Д. (1975). Классическая электродинамика (2-е изд.). Уайли . ISBN  0-471-43132-Х .
• Фурлани, Эдвард П. (2001). Постоянные магниты и электромеханические устройства: материалы, анализ и применение . Академическая пресса . ISBN  0-12-269951-3 .
• Шилль, Р.А. (2003). «Общее соотношение векторного магнитного поля круговой токовой петли: более пристальный взгляд». Транзакции IEEE по магнетизму . 39 (2): 961–967. Бибкод : 2003ITM....39..961S . дои : 10.1109/TMAG.2003.808597 .