Davydov soliton

Квантовая динамика давыдовского солитона с $\chi =35$ pN генерируется путем начального ступенчатого распределения энергии амида I по Гауссу по 3 пептидным группам на N-конце одного шипа α-спирали, состоящего из 40 пептидных групп (проходящих вдоль оси x ) в течение периода 125 пикосекунд. Квантовые вероятности $|a_{n}|^{2}$ возбуждения амида I показаны синим цветом вдоль оси z . Различия смещений фононной решетки $b_{n}-b_{n-1}$ (измеренные в пикометрах) показаны красным вдоль оси y . Солитон образуется за счет самолокализации энергии амида I за счет наведенного искажения решетки.

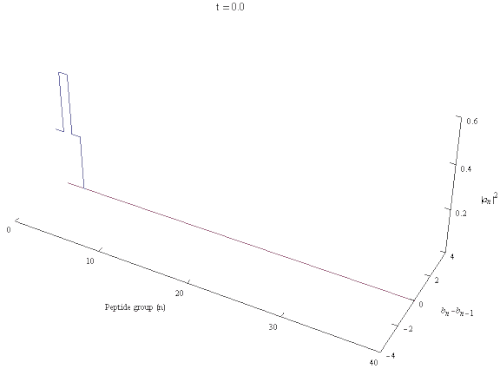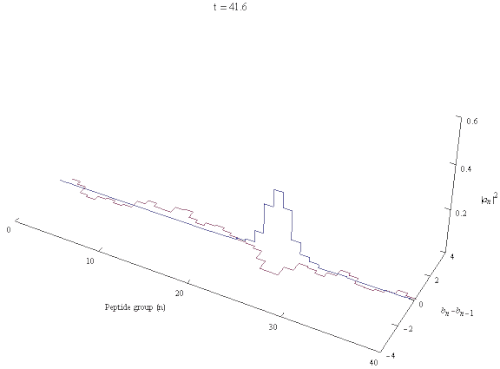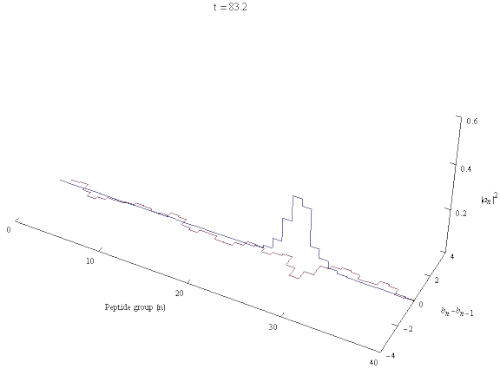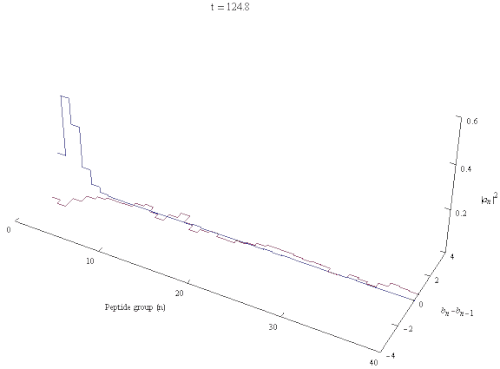
В квантовой биологии ( солитон Давыдова в честь советского украинского физика Александра Давыдова ) — квазичастица представляющая собой возбуждение, распространяющееся вдоль самозахваченных амидных групп I внутри α-спиралей белков , . Это решение гамильтониана Давыдова .

Модель Давыдова описывает взаимодействие колебаний амида I с водородными связями , стабилизирующими α-спирали белков. Элементарные возбуждения внутри α-спирали представляют собой фононы , соответствующие деформационным колебаниям решетки, и экситоны , описывающие внутренние амидные I возбуждения пептидных групп . Если обратиться к атомной структуре участка α-спирали белка, то механизм создания давыдовского солитона (полярона, экситона) можно описать следующим образом: колебательная энергия валентных C=O (или амидного I), осцилляторов локализованная на α-спираль действует посредством эффекта фононной связи, искажая структуру α-спирали, в то время как спиральное искажение снова реагирует посредством фононной связи, захватывая энергию колебаний амида I и предотвращая ее рассеивание. Этот эффект называется самолокализацией или самозахватом . Солитоны , в которых энергия распределена с сохранением винтовой симметрии , динамически неустойчивы, и такие однажды образовавшиеся симметричные солитоны быстро распадаются при распространении. С другой стороны, асимметричный солитон, спонтанно нарушающий локальную трансляционную и спиральную симметрию, обладает наименьшей энергией и является устойчивым локализованным объектом.

Гамильтониан Давыдова

Давыдова Гамильтониан формально подобен гамильтониану Фрелиха-Гольштейна для взаимодействия электронов с поляризуемой решеткой. Таким образом, гамильтониан оператора энергии ${\hat {H}}$ является

${\hat {H}}={\hat {H}}_{\text{ex}}+{\hat {H}}_{\text{ph}}+{\hat {H}}_{\text{int}}$

где ${\hat {H}}_{\text{ex}}$ – экситонный гамильтониан , описывающий движение возбуждений амида I между соседними узлами; ${\hat {H}}_{\text{ph}}$ — фононный гамильтониан , который описываетколебания ​ решетки ​ ; и ${\hat {H}}_{\text{int}}$ – взаимодействия гамильтониан , описывающий взаимодействие возбуждения амида I с решеткой.

Экситонный ​ гамильтониан ${\hat {H}}_{\text{ex}}$ является

${\begin{aligned}{\hat {H}}_{\text{ex}}=&\sum _{n,\alpha }E_{0}{\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha }\\&-J_{1}\sum _{n,\alpha }\left({\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n+1,\alpha }+{\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n-1,\alpha }\right)\\&+J_{2}\sum _{n,\alpha }\left({\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha +1}+{\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha -1}\right)\end{aligned}}$

где индекс $n=1,2,\cdots ,N$ подсчитывает пептидные группы вдоль α-спирали, индекс $\alpha =1,2,3$ считает каждый шип α-спирали, $E_{0}=32.8$ z J – энергия амида Iвибрация (растяжение СО), $J_{1}=0.155$ z J - энергия диполь - дипольной связи между конкретной амидной связью I и теми, кто находится впереди и позади вдоль того же позвоночника, $J_{2}=0.246$ z J – этоэнергия диполь-дипольного взаимодействия между конкретной связью амида I и связями на соседних шипах в одной и той же элементарной ячейке белка α-спирали , ${\hat {A}}_{n,\alpha }^{\dagger }$ и ${\hat {A}}_{n,\alpha }$ соответственнооператор бозона рождения и уничтожения для экситона амида I в пептидной группе $(n,\alpha )$.

Фононный ​ гамильтониан ${\hat {H}}_{\text{ph}}$ является

${\hat {H}}_{\text{ph}}={\frac {1}{2}}\sum _{n,\alpha }\left[w_{1}({\hat {u}}_{n+1,\alpha }-{\hat {u}}_{n,\alpha })^{2}+w_{2}({\hat {u}}_{n,\alpha +1}-{\hat {u}}_{n,\alpha })^{2}+{\frac {{\hat {p}}_{n,\alpha }^{2}}{M_{n,\alpha }}}\right]$

где ${\hat {u}}_{n,\alpha }$ – оператор смещения из положения равновесия пептидной группы $(n,\alpha )$, ${\hat {p}}_{n,\alpha }$ — оператор импульса пептидной группы $(n,\alpha )$, $M_{n,\alpha }$ - масса пептидной группы $(n,\alpha )$, $w_{1}=13-19.5$ Н / м — эффективный коэффициент упругости решетки ( пружинная жесткость водородной связи ) и $w_{2}=30.5$ Н / м – боковая связь между шипами.

Наконец, взаимодействия гамильтониан ${\hat {H}}_{\text{int}}$ является

${\hat {H}}_{\text{int}}=\chi \sum _{n,\alpha }\left[({\hat {u}}_{n+1,\alpha }-{\hat {u}}_{n,\alpha }){\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha }\right]$

где $\chi =35-62$ p N — ангармонический параметр, возникающий в результате связи между экситоном и смещениями решетки (фононом) и параметризующий силу экситон - фононного взаимодействия . Значение этого параметра для α-спирали определено путем сравнения теоретически рассчитанных форм линий поглощения с экспериментально измеренными.

Davydov soliton properties

Существует три возможных фундаментальных подхода к выводу уравнений движения из гамильтониана Давыдова:

• квантовый подход , в котором как колебания амида I ( экситоны ), так и движение узлов решетки ( фононы ) рассматриваются квантовомеханически;
• смешанный квантово-классический подход , в котором колебание амида I рассматривается квантовомеханически, но решетка является классической;
• классический подход , в котором как амид I, так и движения решетки рассматриваются классически.

Математические методы, используемые для анализа солитона Давыдова, аналогичны тем, которые были разработаны в теории поляронов. В этом контексте солитон Давыдова соответствует полярону, который :

• большой, поэтому приближение предела континуума оправдано,
• акустический , поскольку самолокализация возникает за счет взаимодействия с акустическими модами решетки,
• слабо связаны , поскольку ангармоническая энергия мала по сравнению с шириной полосы фононов.

Солитон Давыдова является квантовой квазичастицей и подчиняется принципу неопределенности Гейзенберга . Таким образом, любая модель, не предполагающая трансляционной инвариантности, ошибочна по своей конструкции. Предположение о том, что солитон Давыдова локализован на 5 витках α-спирали, приводит к значительной неопределенности в скорости солитона . $\Delta v=133$ м/с — факт, который неочевиден, если моделировать солитон Давыдова как классический объект.