Полярон

Чтобы узнать о вымышленной частице, см. Полярон (вымышленная частица) .

Не путать с поляритоном .

Полярон используемая — это квазичастица, в физике конденсированного состояния для понимания взаимодействия между электронами и атомами в твердом материале. Концепция полярона была предложена Львом Ландау в 1933 году. и Соломон Пекар в 1946 году. чтобы описать электрон, движущийся в диэлектрическом кристалле , где атомы смещаются из своих положений равновесия, чтобы эффективно экранировать заряд электрона, известный как фононное облако. Это снижает подвижность электронов электронов и увеличивает эффективную массу .

Общая концепция полярона была расширена для описания других взаимодействий между электронами и ионами в металлах, которые приводят к связанному состоянию или снижению энергии по сравнению с невзаимодействующей системой. Основная теоретическая работа была сосредоточена на решении Фрелиха и Гольштейна гамильтонианов . Это все еще активная область исследований по поиску точных численных решений для случая одного или двух электронов в большой кристаллической решетке , а также для изучения случая многих взаимодействующих электронов.

С экспериментальной точки зрения поляроны важны для понимания самых разных материалов. Подвижность электронов в полупроводниках может быть значительно уменьшена за счет образования поляронов. Органические полупроводники также чувствительны к поляронным эффектам, что особенно актуально при разработке органических солнечных элементов , эффективно переносящих заряд. Поляроны также важны для интерпретации оптической проводимости этих типов материалов.

Полярон, фермионную квазичастицу , не следует путать с поляритоном , бозонной квазичастицей, аналогичной гибридизованному состоянию между фотоном и оптическим фононом.

Теория полярона

Энергетический спектр электрона, движущегося в периодическом потенциале жесткой кристаллической решетки , называется спектром Блоха и состоит из разрешенных и запрещенных зон. Электрон с энергией внутри разрешенной зоны движется как свободный электрон, но имеет эффективную массу , отличную от массы электрона в вакууме. Однако кристаллическая решетка деформируема и смещения атомов (ионов) из положений равновесия описываются фононами . Электроны взаимодействуют с этими смещениями, и это взаимодействие известно как электрон-фононная связь. Один из возможных сценариев был предложен в плодотворной статье Льва Ландау 1933 года , который включает в себя создание дефекта решетки, такого как F-центр , и захват электрона этим дефектом. Другой сценарий был предложен Соломоном Пекаром , который предполагает одевание электрона решеточной поляризацией (облаком виртуальных полярных фононов). Такой электрон с сопутствующей деформацией свободно перемещается по кристаллу, но с увеличенной эффективной массой. Пекар придумал для этого носителя заряда термин «полярон» .

Ландо и указывая заложил основу теории полярона. Заряд, помещенный в поляризующуюся среду, будет экранироваться. Теория диэлектрика описывает это явление путем индукции поляризации вокруг носителя заряда. Наведенная поляризация будет следовать за носителем заряда, когда он движется через среду. Носитель вместе с наведенной поляризацией рассматривается как единое целое, которое называется поляроном (см. рис. 1).

Хотя теория поляронов изначально была разработана для электронов, не существует фундаментальной причины, по которой это не могла бы быть какая-либо другая заряженная частица, взаимодействующая с фононами. Действительно, другие заряженные частицы, такие как (электронные) дырки и ионы, обычно следуют теории полярона. Например, протон полярон был идентифицирован экспериментально в 2017 году. и на керамических электролитах после того, как была выдвинута гипотеза о его существовании.

Рис. 1: Вид полярона художником. Электрон проводимости в ионном кристалле или полярном полупроводнике отталкивает отрицательные ионы и притягивает положительные ионы. Возникает самоиндуцированный потенциал, который действует обратно на электрон и изменяет его физические свойства.

Таблица 1: Константы связи Фрелиха

Материал	а	Материал	а
InSb	0.023	К	2.5
InAs	0.052	ТлБр	2.55
GaAs	0.068	КБр	3.05
Зазор	0.20	РБИ	3.16
CdTe	0.29	Би 12 SiO 20	3.18
ZnSe	0.43	КдФ 2	3.2
CDS	0.53	КСl	3.44
АгБр	1.53	CSI	3.67
AgCl	1.84	СрТиО 3	3.77
α-Al 2 O 3	2.40	RbCl	3.81

Обычно в ковалентных полупроводниках связь электронов с деформацией решетки слабая и поляроны не образуются. В полярных полупроводниках электростатическое взаимодействие с наведенной поляризацией сильное и поляроны образуются при низкой температуре, если их концентрация невелика и экранирование неэффективно. Другой класс материалов, в которых наблюдаются поляроны, — молекулярные кристаллы , где взаимодействие с молекулярными колебаниями может быть сильным. В случае полярных полупроводников взаимодействие с полярными фононами описывается гамильтонианом Фрелиха. С другой стороны, взаимодействие электронов с молекулярными фононами описывается гамильтонианом Гольштейна. Обычно модели, описывающие поляроны, можно разделить на два класса. Первый класс представляет собой континуальные модели, в которых пренебрегается дискретностью кристаллической решетки. В этом случае поляроны слабо или сильно связаны в зависимости от того, мала или велика энергия связи полярона по сравнению с частотой фонона. Вторым классом обычно рассматриваемых систем являются решеточные модели поляронов. В этом случае могут быть малые или большие поляроны, в зависимости от относительного размера радиуса полярона и постоянной решетки. а .

Электрон проводимости в ионном кристалле или полярном полупроводнике является прототипом полярона. Герберт Фрелих предложил модельный гамильтониан для этого полярона, с помощью которого его динамика трактуется квантовомеханически (гамильтониан Фрелиха). Сила электрон-фононного взаимодействия определяется безразмерной константой связи $\alpha =(e^{2}/\kappa )(m/2\hbar ^{3}\omega )^{1/2}$. Здесь $m$ - масса электрона, $\omega$ - фононная частота и $\kappa ^{-1}={\epsilon }_{\infty }^{-1}-{\epsilon }_{0}^{-1}$, ${\epsilon }_{0}$, ${\epsilon }_{\infty }$ — статическая и высокочастотная диэлектрическая проницаемость. В таблице 1 приведена константа взаимодействия Фрелиха для некоторых твердых веществ. Гамильтониан Фрелиха для одного электрона в кристалле с использованием обозначений второго квантования :

$H=H_{\rm {e}}+H_{\rm {ph}}+H_{\rm {e-ph}}$

$H_{\rm {e}}=\sum _{k,s}\xi (k,s)c_{k,s}^{\dagger }c_{k,s}$

$H_{\rm {ph}}=\sum _{q,v}\omega _{q,v}a_{q,v}^{\dagger }a_{q,v}$

$H_{\rm {e-ph}}={\frac {1}{\sqrt {2N}}}\sum _{k,s,q,v}\gamma (\alpha ,q,k,v)\omega _{qv}(c_{k,s}^{\dagger }c_{k-q,s}a_{q,v}+c_{k-q,s}^{\dagger }c_{k,s}a_{q,v}^{\dagger })$

Точная форма γ зависит от материала и типа фонона, используемого в модели. В случае однополярной моды $\gamma (q)=i\hbar \omega ({\frac {4\pi \alpha }{V_{0}}}({\frac {\hbar }{m\omega }})^{1/2})^{1/2}{\frac {1}{q}}$, здесь $V_{0}$ – объем элементарной ячейки. В случае молекулярного кристалла γ обычно не зависит от импульса. Подробное расширенное обсуждение вариаций гамильтониана Фрелиха можно найти у Дж. Т. Девриса и А. С. Александрова. Термины «полярон Фрелиха» и «большой полярон» иногда используются как синонимы, поскольку гамильтониан Фрелиха включает в себя континуальное приближение и дальнодействующие силы. Не существует точного решения для гамильтониана Фрелиха с продольными оптическими (LO) фононами и линейными $\gamma$ (наиболее часто рассматриваемый вариант полярона Фрелиха), несмотря на обширные исследования.

Несмотря на отсутствие точного решения, известны некоторые приближения свойств поляронов.

Физические свойства полярона отличаются от свойств полосовой несущей. Полярон характеризуется своей собственной энергией $\Delta E$, эффективная масса $m^{*}$ а также по его характерной реакции на внешние электрические и магнитные поля (например, подвижность постоянного тока и коэффициент оптического поглощения).

Когда связь слабая ( $\alpha$ мала), собственную энергию полярона можно аппроксимировать как:

${\frac {\Delta E}{\hbar \omega }}\approx -\alpha -0.015919622\alpha ^{2},\qquad \qquad \qquad (1)\,$

и масса полярона $m*$, которую можно измерить с помощью экспериментов по циклотронному резонансу, больше массы зоны $m$ носителя заряда без самоиндуцированной поляризации:

${\frac {m^{*}}{m}}\approx 1+{\frac {\alpha }{6}}+0.0236\alpha ^{2}.\qquad \qquad \qquad (2)$

Когда связь сильная (большое α), вариационный подход Ландау и Пекара показывает, что собственная энергия пропорциональна α², а масса полярона масштабируется как α ⁴. Вариационный расчет Ландау–Пекара. дает верхнюю оценку собственной энергии полярона $E<-C_{PL}\alpha ^{2}$, справедливо для всех α , где $C_{PL}$ — константа, определяемая решением интегро-дифференциального уравнения . В течение многих лет оставался открытым вопрос, является ли это выражение асимптотически точным при стремлении α к бесконечности. Наконец, Донскер и Варадхан, применив теорию больших уклонений к формулировке интеграла по траекториям Фейнмана для собственной энергии, показал большую точность этой формулы Ландау – Пекара. Позже Либ и Томас дал более короткое доказательство с использованием более традиционных методов и с явными оценками поправок нижнего порядка к формуле Ландау – Пекара.

Фейнман ввел вариационный принцип для интегралов по траекториям для изучения полярона. Он смоделировал взаимодействие между электроном и модами поляризации посредством гармонического взаимодействия между гипотетической частицей и электроном. Анализ точно решаемой («симметричной») модели 1D-полярона. Схемы Монте-Карло и другие численные схемы продемонстрировать замечательную точность подхода Фейнмана к энергии основного состояния полярона, основанного на интеграле по траекториям. Впоследствии были исследованы экспериментально более доступные свойства полярона, такие как его подвижность и оптическое поглощение.

В пределе сильной связи $\alpha \gg 1$, спектр возбужденных состояний полярона начинается с полярон-фононных связанных состояний с энергиями менее $\hbar \omega _{0}$, где $\omega _{0}$ – частота оптических фононов.

В решеточных моделях основным параметром является энергия связи полярона: $E_{p}={\frac {1}{2N}}\sum _{q}|\gamma (q)|^{2}/\hbar \omega$, здесь суммирование ведется по зоне Бриллюэна. Обратите внимание, что эта энергия связи чисто адиабатическая, т. е. не зависит от ионных масс. Для полярных кристаллов значение энергии связи полярона строго определяется диэлектрическими проницаемостями $\epsilon _{0}$, $\epsilon _{\infty }$, и составляет порядка 0,3-0,8 эВ. Если энергия связи полярона $E_{p}$ меньше интеграла прыжка t, большой полярон образуется при каком-то типе электрон-фононных взаимодействий. В случае, когда $E_{p}>t$ образуется малый полярон. В теории решеточных поляронов имеются два предельных случая. В физически важном адиабатическом пределе $t\gg \hbar \omega$ все члены, включающие ионные массы, сокращаются, и образование полярона описывается нелинейным уравнением Шредингера с неадиабатической поправкой, описывающей перенормировку частоты фононов и туннелирование полярона. В противоположном пределе $t\ll \hbar \omega$ теория представляет собой расширение $t/\hbar \omega$.

поглощение

Выражение для магнитооптического поглощения полярона имеет вид:

$\Gamma (\Omega )\propto -{\frac {\operatorname {Im} \Sigma (\Omega )}{\left[\Omega -\omega _{\mathrm {c} }-\operatorname {Re} \Sigma (\Omega )\right]^{2}+\left[\operatorname {Im} \Sigma (\Omega )\right]^{2}}}.\qquad \qquad \qquad (3)$

Здесь, $\omega _{c}$ – циклотронная частота для электрона в жесткой зоне. Магнитооптическое поглощение Γ(Ω) на частоте Ω принимает вид Σ(Ω) — это так называемая «функция памяти», описывающая динамику полярона. Σ(Ω) зависит также от α, β и $\omega _{c}$.

В отсутствие внешнего магнитного поля ( $\omega _{c}=0$) спектр оптического поглощения (3) полярона при слабой связи определяется поглощением энергии излучения, которое переизлучается в виде LO-фононов. При большей муфте $\alpha \geq 5.9$полярон может совершать переходы в относительно стабильное внутреннее возбужденное состояние, называемое «релаксованно-возбужденным состоянием» (РЭС) (см. рис. 2). Пик РЭС в спектре также имеет фононную боковую полосу, связанную с переходом типа Франка–Кондона.

Рис.2. Оптическое поглощение полярона при $\alpha =5$ и 6. Пик RES очень интенсивен по сравнению с пиком Франка-Кондона (FC).

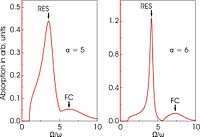
Сравнение результатов DSG со спектрами оптической проводимости , полученными безаппроксимационным численным методом и приближенные аналитические подходы приведены в ссылке.

Расчеты оптической проводимости полярона Фрелиха, выполненные в рамках метода Diagrammatic Quantum Monte Carlo, см. рис. 3, полностью подтверждают результаты вариационного подхода с интегралом по траекториям. в $\alpha \lesssim 3.$ В режиме промежуточной связи $3<\alpha <6,$ низкоэнергетическое поведение и положение максимума спектра оптической проводимости исх. внимательно следуйте предсказанию Девриза. Между двумя подходами в режиме промежуточной и сильной связи имеются следующие качественные различия: в работе: доминирующий пик расширяется, а второй пик не развивается, вместо этого возникает плоское плечо в спектре оптической проводимости при $\alpha =6$. Такое поведение можно объяснить оптическими процессами с участием двух или более фононов. Природа возбужденных состояний полярона требует дальнейшего изучения.

Рис. 3: Спектры оптической проводимости, рассчитанные с помощью диаграммного квантового метода Монте-Карло (светлые кружки), в сравнении с расчетами DSG (сплошные линии).

Приложение достаточно сильного внешнего магнитного поля позволяет удовлетворить условию резонанса $\Omega =\omega _{\mathrm {c} }+\operatorname {Re} \Sigma (\Omega )$, который {(для $\omega _{c}<\omega$)} определяет частоту поляронного циклотронного резонанса. Из этого условия также можно получить циклотронную массу полярона. Использование наиболее точных теоретических поляронных моделей для оценки $\Sigma (\Omega )$, экспериментальные циклотронные данные могут быть хорошо объяснены.

Доказательства поляронного характера носителей заряда в AgBr и AgCl были получены в ходе высокоточных экспериментов по циклотронному резонансу во внешних магнитных полях до 16 Тл. Всесвязное магнитопоглощение, рассчитанное в работе, приводит к лучшему количественному согласию теории и эксперимента для AgBr и AgCl. Эта количественная интерпретация эксперимента по циклотронному резонансу в AgBr иAgCl по теории Петерса предоставил одну из наиболее убедительных и ярких демонстраций свойств полярона Фрелиха в твердых телах.

Экспериментальные данные по магнитополяронному эффекту, полученные с помощью методов фотопроводимости дальнего инфракрасного диапазона, применены для изучения энергетического спектра мелких доноров в полярных полупроводниковых слоях CdTe.

Поляронный эффект, значительно превышающий энергию LO-фонона, изучался посредством измерений циклотронного резонанса, например, в полупроводниках II–VI, наблюдаемых в сверхсильных магнитных полях. Резонансный поляронный эффект проявляется при приближении циклотронной частоты к энергии LO-фонона в достаточно сильных магнитных полях.

В решеточных моделях оптическая проводимость определяется формулой:

$\sigma (\Omega )=n_{p}e^{2}a^{2}{\frac {\pi ^{\frac {1}{2}}t^{2}\left(1-e^{\frac {\hbar \Omega }{k_{\rm {B}}T}}\right)}{2\hbar ^{2}\Omega (E_{a}k_{\rm {B}}T)^{1/2}}}\exp \left(-{\frac {(\hbar \Omega -4E_{a})^{2}}{16E_{a}k_{\rm {B}}T}}\right)$

Здесь $E_{a}$ - энергия активации полярона, которая имеет порядок энергии связи полярона. $E_{p}$. Эта формула была выведена и широко обсуждалась в и был проверен экспериментально, например, на фотолегированных исходных соединениях высокотемпературных сверхпроводников.

Поляроны в двух измерениях и в квазидвумерных структурах

Большой интерес к изучению двумерного электронного газа (2ДЭГ) также привел к многочисленным исследованиям свойств поляронов в двух измерениях. Простая модель двумерной поляронной системы состоит из электрона, удерживаемого в плоскости и взаимодействующего посредством взаимодействия Фрелиха с LO-фононами окружающей трехмерной среды. Собственная энергия и масса такого 2D-полярона больше не описываются выражениями, действительными в 3D; для слабой связи их можно аппроксимировать как:

${\frac {\Delta E}{\hbar \omega }}\approx -{\frac {\pi }{2}}\alpha \ -0.06397\alpha ^{2};\qquad \qquad \qquad (4)\,$

${\frac {m^{*}}{m}}\approx 1+{\frac {\pi }{8}}\alpha \ +0.1272348\alpha ^{2}.\qquad \qquad \qquad (5)\,$

Было показано, что существуют простые масштабные соотношения, связывающие физические свойства поляронов в 2D с физическими свойствами поляронов в 3D. Пример такого отношения масштабирования:

${\frac {m_{\rm {2D}}^{*}(\alpha )}{m_{\rm {2D}}}}={\frac {m_{\rm {3D}}^{*}({\frac {3}{4}}\pi \alpha )}{m_{\rm {3D}}}},\qquad \qquad \qquad (6)\,$

где $m_{\mathrm {2D} }^{*}$ ( $m_{\mathrm {3D} }^{*}$) и $m_{\mathrm {2D} }$ ( $m_{\mathrm {3D} }$) — соответственно массы полярона и электронной зоны в 2D (3D).

Эффект удержания полярона Фрелиха заключается в усилении эффективной поляронной связи. Однако многочастичные эффекты имеют тенденцию уравновешивать этот эффект из-за экранирования.

Также в 2D-системах циклотронный резонанс является удобным инструментом для изучения поляронных эффектов. Хотя приходится учитывать и ряд других эффектов (непараболичность электронных зон, эффекты многих тел , природу удерживающего потенциала и т. д.), в циклотронной массе четко проявляется поляронный эффект. Интересная 2D-система состоит из электронов на пленках жидкого гелия. В этой системе электроны соединяются с риплонами жидкого гелия, образуя «рипплополяроны». Эффективная связь может быть относительно большой, и при некоторых значениях параметров может возникнуть самолокализация. Акустическая природа дисперсии рипплонов на длинных волнах является ключевым аспектом захвата.

Обнаружено, что для квантовых ям и сверхрешеток GaAs/Al _x Ga _1−x As поляронный эффект уменьшает энергию мелких донорных состояний в низких магнитных полях и приводит к резонансному расщеплению энергий в сильных магнитных полях. Энергетические спектры таких поляронных систем, как мелкие доноры («связанные поляроны»), например D ₀ и D ⁻ центры представляют собой наиболее полную и детальную поляронную спектроскопию, реализованную в литературе.

В квантовых ямах GaAs/AlAs с достаточно высокой электронной плотностью антипересечение спектров циклотронного резонанса наблюдалось вблизи частоты поперечного оптического (ТО) фонона GaAs, а не вблизи частоты LO-фонона GaAs. Это антипересечение вблизи частоты TO-фонона было объяснено в рамках поляронной теории.

Помимо оптических свойств, изучены многие другие физические свойства поляронов, в том числе возможность самолокализации, перенос поляронов, магнитофононный резонанс и др.

концепции

Важными являются также расширения концепции полярона: акустический полярон, пьезоэлектрический полярон, электронный полярон, связанный полярон, захваченный полярон, спиновый полярон, молекулярный полярон, сольватированные поляроны, поляронный экситон, ян-теллеровский полярон, малый полярон, биполяроны и многополяроны. системы. Подобные расширения концепции используются, например, для изучения свойств сопряженных полимеров, перовскитов с колоссальным магнитосопротивлением, $T_{c}$ сверхпроводники, слоистые сверхпроводники MgB ₂ , фуллерены, квазиодномерные проводники, полупроводниковые наноструктуры.

Возможность того, что поляроны и биполяроны играют роль в высоко- $T_{c}$ сверхпроводники возобновили интерес к физическим свойствам многополяронных систем и, в частности, к их оптическим свойствам. Теоретические исследования были расширены от однополяронных систем до многополяронных.

Новый аспект концепции полярона был исследован для полупроводниковых наноструктур : экситон-фононные состояния не поддаются факторизации в адиабатический анзац-продукт, поэтому неадиабатическая обработка. необходима Неадиабатичность прогрессии экситон-фононных систем приводит к сильному увеличению вероятностей фононных переходов (по сравнению с адиабатическими) и к многофононным оптическим спектрам, существенно отличающимся от Франка–Кондона даже при малых значениях константа электрон-фононного взаимодействия, как и в случае типичных полупроводниковых наноструктур.

В биофизике давыдовский солитон — это распространяющееся вдоль белка α-спирали самолокализованное амидное возбуждение I, являющееся решением гамильтониана Давыдова. Математические методы, используемые для анализа солитона Давыдова, аналогичны тем, которые были разработаны в теории поляронов. В этом контексте солитон Давыдова соответствует полярону , который (i) велик , поэтому приближение предела континуума оправдано, (ii) акустичен, поскольку самолокализация возникает из-за взаимодействия с акустическими модами решетки, и (iii) слабо связан, потому что ангармоническая энергия мала по сравнению с шириной полосы фононов.

Показано, что система примеси в бозе-эйнштейновском конденсате также относится к семейству поляронов. Это позволяет изучить недоступный до сих пор режим сильной связи, поскольку силы взаимодействия можно регулировать извне с помощью резонанса Фешбаха . Недавно это было экспериментально реализовано двумя исследовательскими группами. Существование полярона в бозе-эйнштейновском конденсате было продемонстрировано как для притягивающих, так и для отталкивающих взаимодействий, включая режим сильной связи, и наблюдалось динамически.

См. также

• Экситон
• Сигурд Зинау
• ТИ-полярон