Электронная зонная структура

В физике твердого тела электронная зонная структура (или просто зонная структура ) твердого тела описывает диапазон энергетических уровней , которые электроны могут иметь внутри него, а также диапазоны энергии, которых они могут не иметь (называемые запрещенными зонами или запрещенными зонами). группы ).

Зонная теория выводит эти зоны и запрещенные зоны путем изучения разрешенных квантово-механических волновых функций для электрона в большой периодической решетке атомов или молекул. Теория зон успешно используется для объяснения многих физических свойств твердых тел, таких как удельное электрическое сопротивление и оптическое поглощение , и формирует основу для понимания всех твердотельных устройств (транзисторов, солнечных элементов и т. д.).

возникают полосы и запрещенные Почему зоны

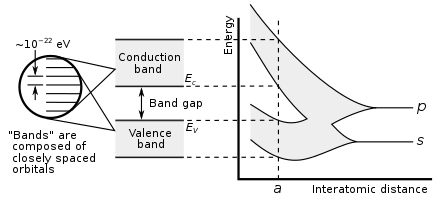
Анимация образования зон и того, как электроны заполняют их в металле и изоляторе.

Образование электронных зон и запрещенных зон можно проиллюстрировать двумя взаимодополняющими моделями электронов в твердых телах. ^[1]^: 161 Первая — это модель почти свободных электронов , в которой предполагается, что электроны почти свободно перемещаются внутри материала. В этой модели электронные состояния напоминают плоские волны свободных электронов и лишь незначительно возмущаются кристаллической решеткой. Эта модель объясняет происхождение закона электронной дисперсии, но объяснение запрещенных зон в этой модели является тонким. ^[2]^: 121

Вторая модель начинается с противоположного предела, в котором электроны тесно связаны с отдельными атомами. Электроны отдельного изолированного атома занимают атомные орбитали с дискретными энергетическими уровнями . Если два атома подходят достаточно близко, так что их атомные орбитали перекрываются, электроны могут туннелировать между атомами. Это туннелирование расщепляет ( гибридизирует ) атомные орбитали на молекулярные орбитали с разными энергиями. ^[2]^{: 117–122}

Аналогично, если большое количество $N$ одинаковых атомов собираются вместе, образуя твердое тело, например кристаллическую решетку , атомные орбитали атомов перекрываются с соседними орбиталями. ^[3] Каждый дискретный энергетический уровень распадается на $N$ уровней, каждый из которых имеет разную энергию. Поскольку число атомов в макроскопическом куске твердого тела очень велико ( $N$ ~10 ²²) число орбиталей очень велико и поэтому они очень близко расположены по энергии (порядка 10 ⁻²² эВ ). Энергия соседних уровней настолько близка друг к другу, что их можно рассматривать как континуум, энергетическую зону.

Такое образование полос в основном свойственно внешним электронам ( валентным электронам ) в атоме, которые участвуют в химической связи и электропроводности . Внутренние электронные орбитали перекрываются незначительно, поэтому их зоны очень узкие.

Запрещенные зоны — это, по сути, оставшиеся диапазоны энергии, не охваченные какой-либо зоной из-за конечной ширины энергетических зон. Полосы имеют разную ширину, причем ширина зависит от степени перекрытия атомных орбиталей , из которых они возникают. Две соседние полосы могут быть просто недостаточно широкими, чтобы полностью охватить диапазон энергии. Например, полосы, связанные с остовными орбиталями (такими как 1s-электроны ), чрезвычайно узки из-за небольшого перекрытия между соседними атомами. В результате между основными полосами обычно возникают большие запрещенные зоны. Более высокие полосы включают в себя сравнительно большие орбитали с большим перекрытием, которые становятся все шире при более высоких энергиях, так что при более высоких энергиях не остается запрещенных зон.

Основные понятия [ править ]

теории зонной Предположения и ограничения структуры

Зонная теория — это лишь приближение к квантовому состоянию твердого тела, которое применимо к твердым телам, состоящим из множества одинаковых атомов или молекул, связанных вместе. Вот предположения, необходимые для справедливости зонной теории:

Система бесконечного размера : чтобы полосы были непрерывными, кусок материала должен состоять из большого количества атомов. Поскольку макроскопический кусок материала содержит порядка 10 ²² атомы, это не является серьезным ограничением; микроскопических размеров Зонная теория применима даже к транзисторам в интегральных схемах . С модификациями концепция зонной структуры также может быть распространена на системы, которые являются «большими» только в некоторых измерениях, таких как двумерные электронные системы .
Гомогенная система : полосовая структура является внутренним свойством материала, которое предполагает, что материал является однородным. Практически это означает, что химический состав материала должен быть однородным по всей детали.
Неинтерактивность : зонная структура описывает «одноэлектронные состояния». Существование этих состояний предполагает, что электроны движутся в статическом потенциале, не взаимодействуя динамически с колебаниями решетки , другими электронами, фотонами и т. д.

Вышеупомянутые предположения нарушаются в ряде важных практических ситуаций, и использование зонной структуры требует внимательного контроля за ограничениями зонной теории:

Неоднородности и интерфейсы. Вблизи поверхностей, стыков и других неоднородностей объемная зонная структура нарушается. Имеют место не только локальные мелкомасштабные нарушения (например, поверхностные состояния или примесные состояния внутри запрещенной зоны), но и локальные дисбалансы зарядов. Эти дисбалансы зарядов имеют электростатические эффекты, которые распространяются глубоко в полупроводники, изоляторы и вакуум (см. Легирование , изгиб зон ).
Аналогичным образом, большинство электронных эффектов ( емкость , электрическая проводимость , экранирование электрического поля ) связаны с физикой прохождения электронов через поверхности и/или вблизи интерфейсов. Полное описание этих эффектов в картине зонной структуры требует, по крайней мере, элементарной модели электрон-электронных взаимодействий (см. Объемный заряд , изгиб зоны ).
Малые системы: Для систем, которые малы по всем измерениям (например, маленькая молекула или квантовая точка ), не существует непрерывной зонной структуры. Переход между малыми и большими измерениями — это область мезоскопической физики .
Сильно коррелированные материалы (например, изоляторы Мотта ) просто невозможно понять в терминах одноэлектронных состояний. Электронные зонные структуры этих материалов плохо определены (или, по крайней мере, не определены однозначно) и не могут предоставлять полезную информацию об их физическом состоянии.

и волновые Кристаллическая симметрия векторы

Рис. 2. График зонной структуры Si , Ge , GaAs и InAs, построенный с использованием модели сильной связи. Обратите внимание, что Si и Ge являются материалами с непрямой запрещенной зоной, а GaAs и InAs - с прямой.

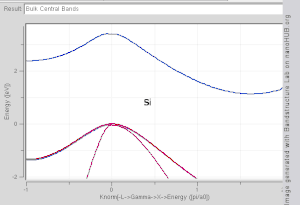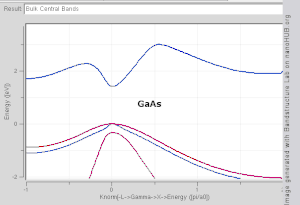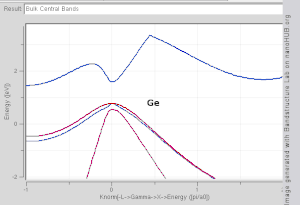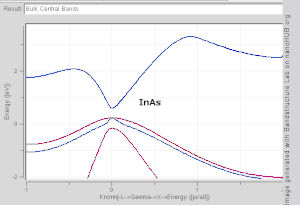
В расчетах зонной структуры используется периодическая природа кристаллической решетки и ее симметрия. Одноэлектронное уравнение Шредингера решается для электрона в периодическом решеточном потенциале, в результате чего принимаются блоховские электроны в качестве решений . $\psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} ),$ где $k$ называется волновым вектором. Для каждого значения $k$ существует несколько решений уравнения Шредингера, отмеченных $n$ , индексом зоны, который просто нумерует энергетические зоны.Каждый из этих энергетических уровней плавно развивается с изменением $k$ , образуя гладкую полосу состояний. Для каждой зоны мы можем определить функцию $En, (k)$ которая является уравнением дисперсии для электронов в этой зоне.

Волновой вектор принимает любое значение внутри зоны Бриллюэна , которая представляет собой многогранник в пространстве волнового вектора ( обратной решетки ), связанный с решеткой кристалла.Волновые векторы вне зоны Бриллюэна просто соответствуют состояниям, которые физически идентичны состояниям внутри зоны Бриллюэна.Особым точкам/линиям высокой симметрии в зоне Бриллюэна присвоены такие метки, как Γ, Δ, Λ, Σ (см. рис. 1).

функцию волнового вектора, так как для этого потребуется построить график в четырехмерном пространстве $E$ в зависимости от $k x$ , $ky,$ Трудно визуализировать форму полосы как $k z$ . В научной литературе часто встречаются графики зонной структуры , на которых показаны значения $En k (вдоль прямых линий, соединяющих точки симметрии, часто обозначаемых Δ)$ для значений $k$ , Λ, Σ или [100], [111] и [110] соответственно. ^[4]^[5] Другой метод визуализации зонной структуры — построить изоповерхность с постоянной энергией в пространстве волновых векторов, показывающую все состояния с энергией, равной определенному значению. Изоповерхность состояний с энергией, равной уровню Ферми, называется поверхностью Ферми .

Энергетические запрещенные зоны можно классифицировать с помощью волновых векторов состояний, окружающих запрещенную зону:

Прямая запрещенная зона : состояние с самой низкой энергией над запрещенной зоной имеет тот же $k$ , что и состояние с самой высокой энергией под запрещенной зоной.
Косвенная запрещенная зона : ближайшие состояния выше и ниже запрещенной зоны не имеют одинакового $значения k$ .

: зонные структуры в некристаллических телах Асимметрия твердых

Хотя электронные зонные структуры обычно связаны с кристаллическими материалами, квазикристаллические и аморфные твердые тела также могут иметь запрещенную зону. Их несколько сложнее изучать теоретически, поскольку им не хватает простой симметрии кристалла, и обычно невозможно определить точный закон дисперсии. В результате практически все существующие теоретические работы по электронной зонной структуре твердых тел сосредоточены на кристаллических материалах.

Плотность состояний [ править ]

Функция плотности состояний $g (E)$ определяется как количество электронных состояний на единицу объема, на единицу энергии для энергий электронов, близких $E.$ к

Функция плотности состояний важна для расчетов эффектов на основе зонной теории.В золотом правиле Ферми , вычислении скорости оптического поглощения , учитывается как количество возбудимых электронов, так и количество конечных состояний электрона. Он появляется в расчетах электропроводности , где он определяет количество мобильных состояний, и при вычислении скорости рассеяния электронов, где он определяет количество конечных состояний после рассеяния. ^{[ нужна ссылка ]}

Для энергий внутри запрещенной зоны $g (E) = 0$ .

Заполнение полос [ править ]

При термодинамическом равновесии вероятность заполнения состояния энергии $E$ электроном определяется распределением Ферми-Дирака , термодинамическим распределением, которое учитывает принцип исключения Паули : $f(E)={\frac {1}{1+e^{{(E-\mu )}/{k_{\text{B}}T}}}}$ где:

$k B T$ — произведение постоянной Больцмана и температуры , а
$µ$ — суммарный химический потенциал электронов, или уровень Ферми (в физике полупроводников эту величину чаще обозначают $E F$ ). Уровень Ферми твердого тела напрямую связан с напряжением на этом твердом теле, измеренным вольтметром. Традиционно на диаграммах зонной структуры за ноль энергии принимают уровень Ферми (выбор произвольный).

Плотность электронов в материале представляет собой просто интеграл распределения Ферми – Дирака, умноженный на плотность состояний: $N/V=\int _{-\infty }^{\infty }g(E)f(E)\,dE$

Хотя существует бесконечное число зон и, следовательно, бесконечное число состояний, в эти зоны можно поместить лишь конечное число электронов.Предпочтительное значение числа электронов является следствием электростатики: хотя поверхность материала может быть заряжена, внутренняя часть материала предпочитает быть нейтральной по заряду.Условие зарядовой нейтральности означает, что $N / V$ должно соответствовать плотности протонов в материале. Чтобы это произошло, материал электростатически подстраивается, сдвигая свою зонную структуру вверх или вниз по энергии (тем самым смещая $g (E)$ ), пока он не достигнет правильного равновесия по отношению к уровню Ферми.

Названия зон вблизи уровня Ферми (зона проводимости, валентная зона) [ править ]

Твердое тело имеет бесконечное количество разрешенных зон, так же как атом имеет бесконечное количество энергетических уровней. Однако большинство полос просто имеют слишком высокую энергию и в обычных обстоятельствах ими обычно пренебрегают. ^[6]И наоборот, существуют очень низкоэнергетические полосы, связанные с основными орбиталями (например, 1s-электроны ). Этими низкоэнергетическими основными зонами также обычно пренебрегают, поскольку они всегда остаются заполненными электронами и, следовательно, инертны. ^[7]Аналогично, материалы имеют несколько запрещенных зон по всей своей зонной структуре.

Наиболее важные зоны и запрещенные зоны, имеющие отношение к электронике и оптоэлектронике, — это зоны с энергиями вблизи уровня Ферми.Зонам и запрещенным зонам вблизи уровня Ферми присваиваются специальные названия в зависимости от материала:

В полупроводнике или зонном изоляторе уровень Ферми окружен запрещенной зоной, называемой запрещенной зоной (чтобы отличить ее от других запрещенных зон в зонной структуре). Ближайшая зона выше запрещенной зоны называется зоной проводимости , а ближайшая зона ниже запрещенной зоны называется валентной зоной . Название «валентная зона» было придумано по аналогии с химией, поскольку в полупроводниках (и изоляторах) валентная зона построена из валентных орбиталей .
В металле или полуметалле уровень Ферми находится внутри одной или нескольких разрешенных зон. В полуметаллах зоны обычно называют «зоной проводимости» или «валентной зоной» в зависимости от того, является ли перенос заряда более электронным или дырочным, по аналогии с полупроводниками. Однако во многих металлах зоны не являются ни электронными, ни дырочными, и их часто называют просто «валентной зоной», поскольку они состоят из валентных орбиталей. ^[8] Запрещенные зоны в зонной структуре металла не важны для физики низких энергий, поскольку они слишком далеки от уровня Ферми.

Теория в кристаллах [ править ]

Анзац — это частный случай электронных волн в периодической кристаллической решетке, основанный на теореме Блоха , которая обычно рассматривается в динамической теории дифракции . Каждый кристалл представляет собой периодическую структуру, которую можно охарактеризовать решеткой Браве , и для каждой решетки Браве мы можем определить обратную решетку , которая инкапсулирует периодичность в наборе трех векторов обратной решетки $(b 1, b 2, b 3)$ . Теперь любой периодический потенциал $V (r),$ который имеет ту же периодичность, что и прямая решетка, может быть разложен в ряд Фурье , единственными неисчезающими компонентами которого являются те, которые связаны с векторами обратной решетки. Таким образом, расширение можно записать как: $V(\mathbf {r} )=\sum _{\mathbf {K} }{V_{\mathbf {K} }e^{i\mathbf {K} \cdot \mathbf {r} }}$ где $K знак равно м 1 б 1 + м 2 б 2 + м 3 б 3$ для любого набора целых чисел $(м 1, м 2, м 3)$ .

На основе этой теории можно попытаться предсказать зонную структуру конкретного материала, однако большинство ab initio методов расчета электронной структуры не могут предсказать наблюдаемую запрещенную зону.

электронов Приближение почти свободных

В приближении почти свободных электронов взаимодействия между электронами полностью игнорируются. Это приближение позволяет использовать теорему Блоха , которая утверждает, что электроны в периодическом потенциале имеют волновые функции и энергии, периодические по волновому вектору, вплоть до постоянного фазового сдвига между соседними векторами обратной решетки . Последствия периодичности математически описываются теоремой Блоха, которая утверждает, что волновые функции собственного состояния имеют вид $\Psi _{n,\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n}(\mathbf {r} )$ где функция Блоха $u_{n}(\mathbf {r} )$ периодичен по кристаллической решетке, т.е. $u_{n}(\mathbf {r} )=u_{n}(\mathbf {r} -\mathbf {R} ).$

Здесь индекс $n$ относится к $n$ -й энергетической зоне, волновой вектор $k$ связан с направлением движения электрона, $r$ — положение в кристалле, а $R$ — расположение атомной позиции. ^[9]^: 179

Модель NFE особенно хорошо работает в таких материалах, как металлы, где расстояния между соседними атомами невелики. В таких материалах перекрытие атомных орбиталей и потенциалов соседних атомов относительно велико. В этом случае волновую функцию электрона можно аппроксимировать (модифицированной) плоской волной. Зонная структура такого металла, как алюминий, даже приближается к приближению пустой решетки .

Модель жесткой привязки [ править ]

Противоположная крайность приближению почти свободных электронов предполагает, что электроны в кристалле ведут себя во многом как совокупность составляющих атомов. Эта модель сильной связи предполагает решение независимого от времени одноэлектронного уравнения Шредингера. $\Psi$ хорошо аппроксимируется линейной комбинацией атомных орбиталей $\psi _{n}(\mathbf {r} )$ . ^[9]^{: 245–248} $\Psi (\mathbf {r} )=\sum _{n,\mathbf {R} }b_{n,\mathbf {R} }\psi _{n}(\mathbf {r} -\mathbf {R} ),$ где коэффициенты $b_{n,\mathbf {R} }$ выбираются так, чтобы дать наилучшее приближенное решение этого вида. Индекс $n$ относится к уровню атомной энергии, а $R$ относится к атомному положению. Более точный подход, использующий эту идею, использует функции Ванье , определяемые следующим образом: ^[9]^{: уравнение. 42 с. 267}^[10] $a_{n}(\mathbf {r} -\mathbf {R} )={\frac {V_{C}}{(2\pi )^{3}}}\int _{\text{BZ}}d\mathbf {k} e^{-i\mathbf {k} \cdot (\mathbf {R} -\mathbf {r} )}u_{n\mathbf {k} };$ в котором $u_{n\mathbf {k} }$ — периодическая часть теоремы Блоха, а интеграл находится по зоне Бриллюэна . Здесь индекс $n$ относится к $n$ -й энергетической зоне кристалла. Функции Ванье локализованы вблизи атомных узлов, например, атомных орбиталей, но, будучи определены в терминах функций Блоха, они точно связаны с решениями, основанными на кристаллическом потенциале. Функции Ванье на разных атомных позициях $R$ ортогональны. Функции Ванье можно использовать для формирования решения Шрёдингера для $n$ -й энергетической зоны следующим образом: $\Psi _{n,\mathbf {k} }(\mathbf {r} )=\sum _{\mathbf {R} }e^{-i\mathbf {k} \cdot (\mathbf {R} -\mathbf {r} )}a_{n}(\mathbf {r} -\mathbf {R} ).$

Модель TB хорошо работает в материалах с ограниченным перекрытием атомных орбиталей и потенциалов соседних атомов. Зонные структуры таких материалов, как Si , GaAs , SiO ₂ и алмаз , например, хорошо описываются TB-гамильтонианами на основе атомных sp ³ орбитали. В переходных металлах смешанная модель TB-NFE используется для описания широкой зоны проводимости NFE и узких встроенных d-зон TB. Радиальные функции атомной орбитальной части функций Ванье проще всего вычислять с помощью методов псевдопотенциала . Расчеты полосовой структуры NFE, TB или комбинированной структуры NFE-TB, ^[11]иногда расширенные аппроксимациями волновой функции, основанными на методах псевдопотенциала, часто используются в качестве экономической отправной точки для дальнейших расчетов.

Модель KKR [ править ]

Метод KKR, также называемый «теорией многократного рассеяния» или методом функции Грина, находит стационарные значения обратной матрицы перехода T, а не гамильтониана. Вариационная реализация была предложена Коррингой , Коном и Ростокером и часто называется методом Корринги-Кона-Ростокера . ^[12]^[13] Наиболее важными особенностями формулировки KKR или функции Грина являются: (1) она разделяет два аспекта проблемы: структуру (положения атомов) и рассеяние (химическую идентичность атомов); и (2) функции Грина обеспечивают естественный подход к локализованному описанию электронных свойств, который можно адаптировать к сплавам и другим неупорядоченным системам. Самая простая форма этого приближения сосредотачивает непересекающиеся сферы (называемые формочками для кексов ) на позициях атомов. Внутри этих областей потенциал, испытываемый электроном, приближается к сферически-симметричному относительно данного ядра. В оставшейся межузельной области экранированный потенциал приближается к константе. Обеспечивается непрерывность потенциала между атомоцентрированными сферами и межузельной областью.

плотности функционала Теория

В современной физической литературе подавляющее большинство электронных структур и зонных диаграмм рассчитываются с использованием теории функционала плотности (DFT), которая является не моделью, а, скорее, теорией, т. е. микроскопической теорией первых принципов физики конденсированного состояния , которая пытается справиться с электрон-электронной задачей многих тел путем введения обменно -корреляционного члена в функционал электронной плотности . Полосы, рассчитанные с помощью DFT, во многих случаях оказываются согласующимися с экспериментально измеренными полосами, например, с помощью фотоэмиссионной спектроскопии с угловым разрешением (ARPES). В частности, форма полосы обычно хорошо воспроизводится методом ДПФ. Но есть также систематические ошибки в полосах ДПФ по сравнению с результатами эксперимента. В частности, DFT, похоже, систематически недооценивает ширину запрещенной зоны в изоляторах и полупроводниках примерно на 30-40%. ^[14]

Принято считать, что ДПФ — это теория, позволяющая предсказывать только свойства основного состояния системы (например, полную энергию , атомную структуру и т. д.), и что свойства возбужденного состояния не могут быть определены с помощью ДПФ. Это заблуждение. В принципе, ДПФ может определить любое свойство (основное или возбужденное состояние) системы с учетом функционала, который отображает плотность основного состояния на это свойство. В этом суть теоремы Хоэнберга–Кона. ^[15] Однако на практике не существует известного функционала, который сопоставлял бы плотность основного состояния с энергиями возбуждения электронов внутри материала. Таким образом, то, что в литературе цитируется как диаграмма полосы ДПФ, представляет собой представление энергий ДПФ Кона-Шэма , то есть энергий фиктивной невзаимодействующей системы, системы Кона-Шэма, которая вообще не имеет физической интерпретации. Электронную структуру Кона-Шэма не следует путать с реальной квазичастичной электронной структурой системы, и для энергий Кона-Шэма не существует теоремы Купманса , как для энергий Хартри-Фока, которые действительно можно рассматривать как приближение для энергий квазичастиц . Следовательно, в принципе, ДПФ на основе Кона-Шэма не является зонной теорией, т. е. не является теорией, подходящей для расчета зон и зонных диаграмм. В принципе, зависящее от времени ДПФ, для расчета истинной зонной структуры можно использовать хотя на практике это часто бывает затруднительно. Популярным подходом является использование гибридных функционалов , которые включают часть точного обмена Хартри – Фока; это приводит к существенному улучшению прогнозируемой ширины запрещенной зоны полупроводников, но менее надежно для металлов и широкозонных материалов. ^[16]

Методы функций Грина и initio приближение - ab GW

Для расчета зон, включающих эффекты многих тел электрон-электронного взаимодействия , можно прибегнуть к так называемым методам функции Грина . Действительно, знание функции Грина системы обеспечивает наблюдаемые как основного (полная энергия), так и возбужденного состояния системы. Полюсы функции Грина — это энергии квазичастиц, зоны твердого тела. Функцию Грина можно рассчитать путем решения уравнения Дайсона, если известна собственная энергия системы. Для реальных систем, таких как твердые тела, собственная энергия является очень сложной величиной, и для решения проблемы обычно необходимы приближения. Одним из таких приближений является приближение GW которую собственная энергия принимает как произведение Σ = GW функции Грина G и динамически экранированного взаимодействия W. , названное так по математической форме , Этот подход более уместен при расчете зонных диаграмм (а также величин за ее пределами, таких как спектральная функция), и его также можно сформулировать полностью ab initio. способ. Приближение GW, по-видимому, обеспечивает ширину запрещенной зоны изоляторов и полупроводников в соответствии с экспериментом и, следовательно, исправляет систематическое недооценивание ДПФ.

среднего Динамическая поля теория

Хотя приближение почти свободных электронов способно описать многие свойства зонных электронных структур, одним из следствий этой теории является то, что она предсказывает одинаковое количество электронов в каждой элементарной ячейке. Если число электронов нечетное, мы могли бы ожидать, что в каждой элементарной ячейке есть неспаренный электрон и, следовательно, валентная зона не заполнена полностью, что делает материал проводником. Однако такие материалы, как CoO , которые имеют нечетное количество электронов на элементарную ячейку, являются изоляторами, что прямо противоречит этому результату. Этот тип материала известен как изолятор Мотта , и для объяснения несоответствия требуется учет детальных электрон-электронных взаимодействий (рассматриваемых только как усредненное влияние на кристаллический потенциал в зонной теории). Модель Хаббарда — это приближенная теория, которая может учитывать эти взаимодействия. Его можно рассматривать непертурбативно в рамках так называемой динамической теории среднего поля , которая пытается преодолеть разрыв между приближением почти свободных электронов и атомным пределом. Однако формально состояния в этом случае не являются невзаимодействующими, и концепция зонной структуры неадекватна для описания этих случаев.

Другие [ править ]

Расчет зонных структур — важная тема теоретической физики твердого тела . Помимо моделей, упомянутых выше, есть и другие модели:

Приближение пустой решетки : «зонная структура» области свободного пространства, разделенной на решетку.
Теория возмущений k·p — это метод, который позволяет приближенно описать зонную структуру с помощью всего нескольких параметров. Этот метод обычно используется для полупроводников , а параметры модели часто определяются экспериментальным путем.
Модель Кронига-Пенни — одномерная модель прямоугольной скважины, полезная для иллюстрации образования полос. Несмотря на свою простоту, он предсказывает множество важных явлений, но не является количественным.
Модель Хаббарда

Зонная структура была обобщена на волновые векторы, которые представляют собой комплексные числа , что привело к так называемой сложной зонной структуре , которая представляет интерес для поверхностей и интерфейсов.

Каждая модель очень хорошо описывает одни типы твердых тел, а другие — плохо. Модель почти свободных электронов хорошо работает для металлов, но плохо для неметаллов. Модель сильной связи чрезвычайно точна для ионных изоляторов, таких как соли галогенидов металлов (например, NaCl ).

Ленточные диаграммы [ править ]

Чтобы понять, как меняется зонная структура относительно уровня Ферми в реальном пространстве, график зонной структуры часто сначала упрощают в виде зонной диаграммы . На зонной диаграмме вертикальная ось представляет собой энергию, а горизонтальная ось представляет реальное пространство. Горизонтальные линии представляют уровни энергии, а блоки представляют собой энергетические диапазоны. Когда горизонтальные линии на этой диаграмме наклонены, энергия уровня или зоны меняется с расстоянием. Схематически это изображает наличие электрического поля внутри кристаллической системы. Зонные диаграммы полезны для сопоставления общих свойств зонной структуры различных материалов друг с другом при контакте друг с другом.

См. также [ править ]

Инженерия запрещенной зоны — процесс изменения зонной структуры материала.
Феликс Блох — пионер теории зонной структуры.
Алан Херрис Уилсон — пионер теории зонной структуры.

Ссылки [ править ]

^ Саймон, Стивен Х. (2013). Оксфордские основы твердого тела . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-150210-1 .
↑ Перейти обратно: Перейти обратно: ^а ^б Гирвин, Стивен М.; Ян, Кун (2019). Современная физика конденсированного состояния . Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-13739-4 .
^ Холгейт, Шэрон Энн (2009). Понимание физики твердого тела . ЦРК Пресс. стр. 177–178. ISBN 978-1-4200-1232-3 .
^ «Архив NSM - Арсенид алюминия-галлия (AlGaAs) - Зонная структура и концентрация носителей» . www.ioffe.ru .
^ «Электронная зонная структура» (PDF) . www.springer.com . Спрингер. п. 24 . Проверено 10 ноября 2016 г.
^ Высокоэнергетические полосы важны для физики дифракции электронов , где электроны могут инжектироваться в материал при высоких энергиях, см. Стерн, Р.; Перри, Дж.; Будро, Д. (1969). «Дисперсионные поверхности низкоэнергетических электронов и зонная структура в трехмерных смешанных отражениях Лауэ и Брэгга». Обзоры современной физики . 41 (2): 275. Бибкод : 1969РвМП...41..275С . дои : 10.1103/RevModPhys.41.275 . .
^ Однако низкоэнергетические полосы важны для эффекта Оже .
^ В меди, например, эффективная масса представляет собой тензор и также меняет знак в зависимости от волнового вектора, как это можно видеть в эффекте Де Хааса – Ван Альфена ; см. https://www.phys.ufl.edu/fermisurface/
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Чарльз Киттель (1996). Введение в физику твердого тела (Седьмое изд.). Нью-Йорк: Уайли. ISBN 978-0-471-11181-8 .
^ Дэниел Чарльз Мэттис (1994). Задача многих тел: энциклопедия точно решаемых моделей в одном измерении . Всемирная научная. п. 340. ИСБН 978-981-02-1476-0 .
^ Уолтер Эшли Харрисон (1989). Электронная структура и свойства твердых тел . Дуврские публикации. ISBN 978-0-486-66021-9 .
^ Джогиндер Сингх Галсин (2001). Рассеяние примесей в металлических сплавах . Спрингер. Приложение C. ISBN 978-0-306-46574-1 .
^ Куон Иноуэ, Кадзуо Отака (2004). Фотонные кристаллы . Спрингер. п. 66. ИСБН 978-3-540-20559-3 .
^ Ассади, М. Хусейн. Н.; Ханаор, Дориан А.Х. (21 июня 2013 г.). «Теоретическое исследование энергетики и магнетизма меди в полиморфах TiO ₂ ». Журнал прикладной физики . 113 (23): 233913–233913–5. arXiv : 1304.1854 . Бибкод : 2013JAP...113w3913A . дои : 10.1063/1.4811539 . ISSN 0021-8979 . S2CID 94599250 .
^ Хоэнберг, П; Кон, В. (ноябрь 1964 г.). «Неоднородный электронный газ» . Физ. Преподобный . 136 (3Б): Б864–Б871. Бибкод : 1964PhRv..136..864H . дои : 10.1103/PhysRev.136.B864 .
^ Пайер, Дж.; Марсман, М.; Хаммер, К.; Кресс, Г.; Гербер, IC; Ангьян, Дж.Г. (2006). «Экранированные гибридные функционалы плотности применительно к твердым телам». J Chem Phys . 124 (15): 154709. Бибкод : 2006JChPh.124o4709P . дои : 10.1063/1.2187006 . ПМИД 16674253 .

Дальнейшее чтение [ править ]

Эшкрофт, Нил и Н. Дэвид Мермин, Физика твердого тела , ISBN 0-03-083993-9
Харрисон, Уолтер А., Элементарная электронная структура , ISBN 981-238-708-0
Харрисон, Уолтер А.; В.А. Бенджамин Псевдопотенциалы в теории металлов , (Нью-Йорк) 1966 г.
Мардер, Майкл П., Физика конденсированного состояния , ISBN 0-471-17779-2
Мартин, Ричард, Электронная структура: основная теория и практические методы , ISBN 0-521-78285-6
Миллман, Джейкоб; Арвин Габриэль, Микроэлектроника , ISBN 0-07-463736-3 , издание Таты МакГроу-Хилл.
Nemoshkalenko, V. V., and N. V. Antonov, Computational Methods in Solid State Physics , ISBN 90-5699-094-2
Омар, М. Али, Элементарная физика твердого тела: принципы и приложения , ISBN 0-201-60733-6
Сингх, Джасприт, Электронные и оптоэлектронные свойства полупроводниковых структур, главы 2 и 3, ISBN 0-521-82379-X
Василеска, Драгица , Учебное пособие по методам зонной структуры (2008)

[1] Саймон, Стивен Х. (2013). Оксфордские основы твердого тела . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-150210-1 .

[girvin-2] Перейти обратно: Перейти обратно: ^а ^б Гирвин, Стивен М.; Ян, Кун (2019). Современная физика конденсированного состояния . Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-13739-4 .

[Holgate-3] Холгейт, Шэрон Энн (2009). Понимание физики твердого тела . ЦРК Пресс. стр. 177–178. ISBN 978-1-4200-1232-3 .

[4] «Архив NSM - Арсенид алюминия-галлия (AlGaAs) - Зонная структура и концентрация носителей» . www.ioffe.ru .

[SpringerBandStructure-5] «Электронная зонная структура» (PDF) . www.springer.com . Спрингер. п. 24 . Проверено 10 ноября 2016 г.

[6] Высокоэнергетические полосы важны для физики дифракции электронов , где электроны могут инжектироваться в материал при высоких энергиях, см. Стерн, Р.; Перри, Дж.; Будро, Д. (1969). «Дисперсионные поверхности низкоэнергетических электронов и зонная структура в трехмерных смешанных отражениях Лауэ и Брэгга». Обзоры современной физики . 41 (2): 275. Бибкод : 1969РвМП...41..275С . дои : 10.1103/RevModPhys.41.275 . .

[7] Однако низкоэнергетические полосы важны для эффекта Оже .

[8] В меди, например, эффективная масса представляет собой тензор и также меняет знак в зависимости от волнового вектора, как это можно видеть в эффекте Де Хааса – Ван Альфена ; см. https://www.phys.ufl.edu/fermisurface/

[Kittel-9] Перейти обратно: Перейти обратно: ^а ^б ^с Чарльз Киттель (1996). Введение в физику твердого тела (Седьмое изд.). Нью-Йорк: Уайли. ISBN 978-0-471-11181-8 .

[Mattis-10] Дэниел Чарльз Мэттис (1994). Задача многих тел: энциклопедия точно решаемых моделей в одном измерении . Всемирная научная. п. 340. ИСБН 978-981-02-1476-0 .

[Harrison-11] Уолтер Эшли Харрисон (1989). Электронная структура и свойства твердых тел . Дуврские публикации. ISBN 978-0-486-66021-9 .

[Galsin-12] Джогиндер Сингх Галсин (2001). Рассеяние примесей в металлических сплавах . Спрингер. Приложение C. ISBN 978-0-306-46574-1 .

[Ohtaka-13] Куон Иноуэ, Кадзуо Отака (2004). Фотонные кристаллы . Спрингер. п. 66. ИСБН 978-3-540-20559-3 .

[14] Ассади, М. Хусейн. Н.; Ханаор, Дориан А.Х. (21 июня 2013 г.). «Теоретическое исследование энергетики и магнетизма меди в полиморфах TiO ₂ ». Журнал прикладной физики . 113 (23): 233913–233913–5. arXiv : 1304.1854 . Бибкод : 2013JAP...113w3913A . дои : 10.1063/1.4811539 . ISSN 0021-8979 . S2CID 94599250 .

[15] Хоэнберг, П; Кон, В. (ноябрь 1964 г.). «Неоднородный электронный газ» . Физ. Преподобный . 136 (3Б): Б864–Б871. Бибкод : 1964PhRv..136..864H . дои : 10.1103/PhysRev.136.B864 .

[Paier-16] Пайер, Дж.; Марсман, М.; Хаммер, К.; Кресс, Г.; Гербер, IC; Ангьян, Дж.Г. (2006). «Экранированные гибридные функционалы плотности применительно к твердым телам». J Chem Phys . 124 (15): 154709. Бибкод : 2006JChPh.124o4709P . дои : 10.1063/1.2187006 . ПМИД 16674253 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]