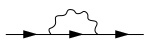
Собственная энергия

В квантовой теории поля энергия, которую частица имеет в результате изменений, которые она вызывает в своем окружении, определяет собственную энергию. $\Sigma$ частицы , и представляет собой вклад в энергию или эффективную массу из-за взаимодействия между частицей и ее окружением. В электростатике энергия, необходимая для формирования распределения зарядов, принимает форму собственной энергии за счет внесения составляющих зарядов из бесконечности, где электрическая сила стремится к нулю. В контексте конденсированного состояния собственная энергия используется для описания вызванной взаимодействием перенормировки массы квазичастицы ( дисперсии ) и времени жизни. Собственная энергия особенно используется для описания электрон-электронных взаимодействий в ферми-жидкостях . Другой пример собственной энергии можно найти в контексте смягчения фононов из-за электрон-фононного взаимодействия.

Характеристики

Математически эта энергия равна так называемому значению на массовой оболочке собственной энергии собственного оператора (или собственного массового оператора ) в импульсно-энергетическом представлении (точнее, $\hbar$ раз это значение). В этом или других представлениях (таких как пространственно-временное представление) собственная энергия наглядно (и экономически) представлена ​​с помощью диаграмм Фейнмана , таких как показанная ниже. На этой конкретной диаграмме три прямые линии со стрелками представляют частицы или распространители частиц , а волнистая линия — взаимодействие между частицами; удалив (или ампутировав ) крайнюю левую и крайнюю правую прямые линии на диаграмме, показанной ниже (эти так называемые внешние линии соответствуют заданным значениям, например, для импульса и энергии, или четырехимпульса ), сохраняется вклад в оператор собственной энергии (например, в представлении импульс-энергия). Используя небольшое количество простых правил, каждую диаграмму Фейнмана можно легко выразить в соответствующей алгебраической форме.

В общем, значение оператора собственной энергии на массовой оболочке в представлении энергии-импульса является комплексным . В таких случаях именно реальная часть этой собственной энергии отождествляется с физической собственной энергией (называемой выше «собственной энергией» частицы); обратная мнимая часть является мерой времени жизни исследуемой частицы. Для ясности элементарные возбуждения, или одетые частицы (см. квазичастицы ), во взаимодействующих системах отличаются от стабильных частиц в вакууме; их функции состояния состоят из сложных суперпозиций собственных состояний лежащей в основе многочастичной системы, которые лишь на мгновение, если вообще ведут себя как те, которые специфичны для изолированных частиц; вышеупомянутое время жизни — это время, в течение которого одетая частица ведет себя так, как если бы она была одиночной частицей с четко определенными импульсом и энергией.

Оператор собственной энергии (часто обозначаемый $\Sigma _{}^{}$и реже на $M_{}^{}$) относится к голым и одетым пропагаторам (часто обозначается $G_{0}^{}$ и $G_{}^{}$ соответственно) через уравнение Дайсона (названное в честь Фримена Дайсона ):

$G=G_{0}^{}+G_{0}\Sigma G.$

Умножение слева на обратное $G_{0}^{-1}$ оператора $G_{0}$ и справа от $G^{-1}$ урожайность

$\Sigma =G_{0}^{-1}-G^{-1}.$

Фотон , и глюон не получают массу в результате перенормировки поскольку калибровочная симметрия защищает их от получения массы. Это следствие идентичности Уорда . W -бозон и Z-бозон получают свою массу посредством механизма Хиггса ; они действительно подвергаются перенормировке массы посредством перенормировки электрослабой теории.

Нейтральные частицы с внутренними квантовыми числами могут смешиваться друг с другом посредством образования виртуальных пар . Основным примером этого явления является смешивание нейтральных каонов . При соответствующих упрощающих предположениях это можно описать без использования квантовой теории поля .

Другое использование

В химии собственная энергия или энергия Борна иона — это энергия, связанная с полем самого иона.

В физике твердого тела и конденсированного состояния собственные энергии и множество связанных с ними свойств квазичастиц рассчитываются методами функции Грина и функции Грина (теория многих тел) взаимодействующих низкоэнергетических возбуждений на основе расчетов электронной зонной структуры . Собственные энергии также находят широкое применение при расчете транспорта частиц через открытые квантовые системы и встраивании подобластей в более крупные системы (например, поверхность полубесконечного кристалла).

См. также

• Квантовая теория поля
• Это пылесосит
• Перенормировка
• Самосила
• ГВ-приближение
• Теория поглотителя Уиллера – Фейнмана

Ссылки

• А. Л. Феттер и Дж. Д. Валецка, Квантовая теория многочастичных систем (McGraw-Hill, Нью-Йорк, 1971); (Дувр, Нью-Йорк, 2003 г.)
• Дж. В. Негеле и Х. Орланд, Квантовые многочастичные системы (Westview Press, Боулдер, 1998).
• А. А. Абрикосов, Л. П. Горьков и И. Е. Дзялошинский (1963): Методы квантовой теории поля в статистической физике Энглвуд Клиффс: Прентис-Холл.
• Алексей Михайлович Цвелик (2007). Квантовая теория поля в физике конденсированного состояния (2-е изд.). Издательство Кембриджского университета. ISBN  978-0-521-52980-8 .
• А. Н. Васильев Теоретико-полевая ренормгруппа в теории критического поведения и стохастической динамике (Routledge Chapman & Hall, 2004); ISBN   0-415-31002-4 ; ISBN   978-0-415-31002-4
• Джон Э. Инглесфилд (2015). Метод встраивания электронной структуры . Издательство ИОП. ISBN  978-0-7503-1042-0 .