Модель свободных электронов

Эта статья о твердотельной модели металлов. Чтобы узнать о модели газа свободных электронов, см. Ферми-газ .

В физике твердого тела модель свободных электронов представляет собой квантовомеханическую модель поведения носителей заряда в металлическом твердом теле. Он был разработан в 1927 г. главным образом Арнольдом Зоммерфельдом , который объединил классическую модель Друде с квантовомеханической статистикой Ферми-Дирака , и поэтому она также известна как модель Друде-Зоммерфельда .

Учитывая свою простоту, он удивительно успешно объясняет многие экспериментальные явления, особенно

• закон Видемана -Франца, связывающий электропроводность и теплопроводность ;
• температурная зависимость электронной теплоемкости ;
• форма электронной плотности состояний ;
• диапазон значений энергии связи;
• электропроводность;
• коэффициент Зеебека термоэлектрического эффекта ;
• термическая электронная эмиссия и автоэлектронная эмиссия из объемных металлов.

Модель свободных электронов разрешила многие противоречия, связанные с моделью Друде, и дала представление о некоторых других свойствах металлов. Модель свободных электронов предполагает, что металлы состоят из квантового электронного газа, в котором ионы практически не играют роли. Модель может быть очень предсказуемой применительно к щелочным и благородным металлам .

Идеи и предположения

В модели свободных электронов учитываются четыре основных предположения:

• Приближение свободных электронов: взаимодействием между ионами и валентными электронами в основном пренебрегают, за исключением граничных условий. Ионы лишь сохраняют нейтральность заряда в металле. В отличие от модели Друде, ионы не обязательно являются источником столкновений.
• Приближение независимых электронов : взаимодействия между электронами игнорируются. Электростатические поля в металлах слабы из-за эффекта экранирования .
• Приближение времени релаксации: существует некоторый неизвестный механизм рассеяния, такой, что вероятность столкновения электронов обратно пропорциональна времени релаксации. $\tau$, который представляет собой среднее время между столкновениями. Столкновения не зависят от электронной конфигурации.
• Принцип Паули : каждое квантовое состояние системы может быть занято только одним электроном. Это ограничение доступных электронных состояний учитывается статистикой Ферми – Дирака (см. также Ферми-газ ). Основные предсказания модели свободных электронов получены с помощью разложения Зоммерфельда занятости Ферми – Дирака для энергий около уровня Ферми .

Название модели происходит от первых двух предположений, поскольку каждый электрон можно рассматривать как свободную частицу с соответствующим квадратичным соотношением между энергией и импульсом.

Кристаллическая решетка явно не учитывается в модели свободного электрона, но квантовомеханическое обоснование было дано годом позже (1928 г.) теоремой Блоха : несвязанный электрон движется в периодическом потенциале, как свободный электрон в вакууме, за исключением масса электрона m _e становится эффективной массой m*, которая может значительно отклоняться от me _e (можно даже использовать отрицательную эффективную массу для описания проводимости электронными дырками ). Эффективные массы могут быть получены из расчетов зонной структуры , которые изначально не учитывались в модели свободных электронов.

По модели Друде

Основная статья: Модель Друде

Многие физические свойства следуют непосредственно из модели Друде , поскольку некоторые уравнения не зависят от статистического распределения частиц. Взятие классического распределения скоростей идеального газа или распределения скоростей ферми-газа только меняет результаты, связанные со скоростью электронов.

В основном, модель свободных электронов и модель Друде предсказывают одинаковую электропроводность постоянного тока σ для закона Ома , то есть

$\mathbf {J} =\sigma \mathbf {E} \quad$ с $\quad \sigma ={\frac {ne^{2}\tau }{m_{e}}},$

где $\mathbf {J}$ плотность тока , $\mathbf {E}$ – внешнее электрическое поле, $n$ - электронная плотность (количество электронов/объем), $\tau$ среднее свободное время и $e$ – электрический заряд электрона .

Другими величинами, которые остаются такими же в модели свободных электронов, как и в модели Друде, являются восприимчивость к переменному току, плазменная частота , магнитосопротивление и коэффициент Холла, связанный с эффектом Холла .

Свойства электронного газа

Основная статья: Ферми-газ

Многие свойства модели свободных электронов следуют непосредственно из уравнений, связанных с ферми-газом, поскольку приближение независимых электронов приводит к ансамблю невзаимодействующих электронов. Для трехмерного электронного газа мы можем определить энергию Ферми как

$E_{\rm {F}}={\frac {\hbar ^{2}}{2m_{e}}}\left(3\pi ^{2}n\right)^{\frac {2}{3}},$

где $\hbar$ – приведенная постоянная Планка . Энергия Ферми определяет энергию электрона с наивысшей энергией при нулевой температуре. Для металлов энергия Ферми на порядок единиц электронвольта превышает минимальную энергию зоны свободных электронов.

В трех измерениях плотность состояний газа фермионов пропорциональна корню квадратному из кинетической энергии частиц.

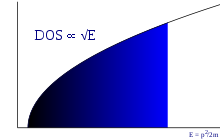
Плотность штатов

Трехмерная плотность состояний (количество энергетических состояний на единицу энергии на объем) невзаимодействующего электронного газа определяется выражением:

$g(E)={\frac {m_{e}}{\pi ^{2}\hbar ^{3}}}{\sqrt {2m_{e}E}}={\frac {3}{2}}{\frac {n}{E_{\rm {F}}}}{\sqrt {\frac {E}{E_{\rm {F}}}}},$

где ${\textstyle E\geq 0}$ - энергия данного электрона. Эта формула учитывает спиновое вырождение, но не учитывает возможный сдвиг энергии из-за дна зоны проводимости . Для 2D плотность состояний постоянна, а для 1D обратно пропорциональна квадратному корню из энергии электрона.

уровень Ферми

Химический потенциал $\mu$ электронов в твердом теле также известен как уровень Ферми и, как и связанная с ним энергия Ферми , часто обозначается $E_{\rm {F}}$. можно Разложение Зоммерфельда использовать для расчета уровня Ферми ( $T>0$) при более высоких температурах как:

$E_{\rm {F}}(T)=E_{\rm {F}}(T=0)\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {T}{T_{\rm {F}}}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {T}{T_{\rm {F}}}}\right)^{4}+\cdots \right],$

где $T$ – температура, и мы определяем ${\textstyle T_{\rm {F}}=E_{\rm {F}}/k_{\rm {B}}}$ как температура Ферми ( $k_{\rm {B}}$ — постоянная Больцмана ). Пертурбативный подход оправдан, поскольку температура Ферми обычно составляет около 10 ⁵ K для металла, следовательно, при комнатной температуре или ниже энергии Ферми. $E_{\rm {F}}(T=0)$ и химический потенциал $E_{\rm {F}}(T>0)$ практически эквивалентны.

Сжимаемость металлов и давление вырождения.

Полная энергия единицы объема (при ${\textstyle T=0}$) также можно вычислить интегрированием по фазовому пространству системы, получим

$u(0)={\frac {3}{5}}nE_{\rm {F}},$

который не зависит от температуры. Сравните с энергией, приходящейся на электрон идеального газа: ${\textstyle {\frac {3}{2}}k_{\rm {B}}T}$, который равен нулю при нулевой температуре. Чтобы идеальный газ имел ту же энергию, что и электронный газ, температура должна быть порядка температуры Ферми. Термодинамически эта энергия электронного газа соответствует давлению при нулевой температуре, определяемому формулой

$P=-\left({\frac {\partial U}{\partial V}}\right)_{T,\mu }={\frac {2}{3}}u(0),$

где ${\textstyle V}$ это объем и ${\textstyle U(T)=u(T)V}$ - полная энергия, производная, выполненная при температуре и константе химического потенциала. Это давление называется давлением вырождения электронов и возникает не из-за отталкивания или движения электронов, а из-за ограничения, согласно которому не более двух электронов (из-за двух значений спина) могут занимать один и тот же энергетический уровень. Это давление определяет сжимаемость или модуль объемного сжатия металла.

$B=-V\left({\frac {\partial P}{\partial V}}\right)_{T,\mu }={\frac {5}{3}}P={\frac {2}{3}}nE_{\rm {F}}.$

Это выражение дает правильный порядок величины модуля объемного сжатия для щелочных и благородных металлов, что показывает, что это давление так же важно, как и другие эффекты внутри металла. Для других металлов необходимо учитывать кристаллическую структуру.

Магнитный отклик

Согласно теореме Бора-Ван Лювена , классическая система, находящаяся в термодинамическом равновесии, не может иметь магнитного отклика. Магнитные свойства материи с точки зрения микроскопической теории являются чисто квантовомеханическими. Для электронного газа полный магнитный отклик является парамагнитным , а его магнитная восприимчивость определяется выражением

$\chi ={\frac {2}{3}}\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} }),$

где ${\textstyle \mu _{0}}$ - диэлектрическая проницаемость вакуума и ${\textstyle \mu _{\rm {B}}}$ это магнетон Бора . Это значение является результатом конкуренции двух вкладов: диамагнитного вклада (известного как диамагнетизм Ландау ), возникающего в результате орбитального движения электронов в присутствии магнитного поля, и парамагнитного вклада (парамагнетизма Паули). Последний вклад в три раза больше по абсолютной величине, чем диамагнитный вклад, и обусловлен спином электрона , собственной квантовой степенью свободы, которая может принимать два дискретных значения и связана с магнитным моментом электрона .

Поправки к модели Друде

Теплоемкость

Дополнительная информация: Электронная удельная теплоемкость.

Одной из открытых проблем в физике твердого тела до появления квантовой механики было понимание теплоемкости металлов . Хотя большинство твердых тел имели постоянную объемную теплоемкость , определяемую законом Дюлонга – Пти, примерно $3nk_{\rm {B}}$при высоких температурах он правильно предсказал свое поведение при низких температурах. В случае металлов, которые являются хорошими проводниками, ожидалось, что электроны также вносят вклад в теплоемкость.

Классический расчет с использованием модели Друде, основанной на идеальном газе, дает объемную теплоемкость, определяемую выражением

$c_{V}^{\text{Drude}}={\frac {3}{2}}nk_{\rm {B}}$.

Если бы это было так, то теплоемкость металлов должна была бы составлять 1,5 от полученной по закону Дюлонга-Пти.

Тем не менее, такой большой дополнительный вклад в теплоемкость металлов никогда не измерялся, что вызывает подозрения в отношении приведенного выше аргумента. Используя расширение Зоммерфельда, можно получить поправки к плотности энергии при конечной температуре и получить объемную теплоемкость электронного газа, определяемую формулой:

$c_{V}=\left({\frac {\partial u}{\partial T}}\right)_{n}={\frac {\pi ^{2}}{2}}{\frac {T}{T_{\rm {F}}}}nk_{\rm {B}}$,

где префактор для $nk_{B}$значительно меньше, чем 3/2, найденная в ${\textstyle c_{V}^{\text{Drude}}}$, примерно в 100 раз меньше при комнатной температуре и намного меньше при более низких ${\textstyle T}$.

Очевидно, что только электронный вклад не предсказывает закон Дюлонга-Пти , т.е. наблюдение о том, что теплоемкость металла остается постоянной при высоких температурах. В этом смысле модель свободных электронов можно улучшить, добавив вклад колебаний кристаллической решетки. Две известные квантовые поправки включают твердотельную модель Эйнштейна и более усовершенствованную модель Дебая . С добавлением последнего объемную теплоемкость металла при низких температурах можно точнее записать в виде:

$c_{V}\approx \gamma T+AT^{3}$,

где $\gamma$ и $A$ являются константами, связанными с материалом. Линейный член возникает из-за электронного вклада, а кубический член - из модели Дебая. При высокой температуре это выражение уже не корректно, электронной теплоемкостью можно пренебречь, а полная теплоемкость металла стремится к константе, определяемой законом Дюлонга-Пти.

Средний свободный путь

Обратите внимание, что без приближения времени релаксации у электронов нет причин отклонять свое движение, поскольку нет взаимодействий, поэтому длина свободного пробега должна быть бесконечной. Модель Друде считала, что средняя длина свободного пробега электронов близка к расстоянию между ионами в материале, подразумевая более ранний вывод о том, что диффузионное движение электронов происходит из-за столкновений с ионами. Вместо этого средние свободные пробеги в модели свободных электронов определяются выражением ${\textstyle \lambda =v_{\rm {F}}\tau }$ (где ${\textstyle v_{\rm {F}}={\sqrt {2E_{\rm {F}}/m_{e}}}}$ — скорость Ферми) и составляют порядка сотен ангстрем , что, по крайней мере, на порядок больше, чем любые возможные классические расчеты. Тогда длина свободного пробега не является результатом электрон-ионных столкновений, а связана с несовершенствами материала, либо из-за дефектов и примесей в металле, либо из-за тепловых флуктуаций.

Теплопроводность и термоЭДС

Хотя модель Друде предсказывает то же значение электропроводности, что и модель свободных электронов, модели предсказывают несколько иную теплопроводность.

Теплопроводность определяется выражением $\kappa =c_{V}\tau \langle v^{2}\rangle /3$ для свободных частиц, которая пропорциональна теплоемкости и длине свободного пробега, которые зависят от модели ( $\langle v^{2}\rangle ^{1/2}$ — средняя (квадратичная) скорость электронов или скорость Ферми в случае модели свободных электронов). Это означает, что соотношение между теплопроводностью и электропроводностью определяется законом Видемана-Франца :

${\frac {\kappa }{\sigma }}={\frac {m_{\rm {e}}c_{V}\langle v^{2}\rangle }{3ne^{2}}}=LT$

где $L$ - число Лоренца, определяемое формулой

$L=\left\{{\begin{matrix}\displaystyle {\frac {3}{2}}\left({\frac {k_{\rm {B}}}{e}}\right)^{2}\;,&{\text{Drude}}\\\displaystyle {\frac {\pi ^{2}}{3}}\left({\frac {k_{\rm {B}}}{e}}\right)^{2}\;,&{\text{free electron model.}}\end{matrix}}\right.$

Модель свободных электронов ближе к измеренному значению $L=2.44\times 10^{-8}$ V ² /К ² в то время как прогноз Друде отличается примерно на половину значения, что не является большой разницей. Близкое предсказание числа Лоренца в модели Друде было результатом того, что классическая кинетическая энергия электрона была примерно в 100 раз меньше, чем в квантовой версии, что компенсировало большое значение классической теплоемкости.

Однако режим Друде предсказывает неправильный порядок величины коэффициента Зеебека (термоэдс), который связывает возникновение разности потенциалов за счет приложения температурного градиента к образцу. $\nabla V=-S\nabla T$. Можно показать, что этот коэффициент $S=-{c_{\rm {V}}}/{|ne|}$, которая прямо пропорциональна теплоемкости, поэтому модель Друде предсказывает константу, которая в сто раз превышает значение модели свободных электронов. В то время как последний получает коэффициент, линейный по температуре и обеспечивающий гораздо более точные абсолютные значения порядка нескольких десятков мкВ/К при комнатной температуре. Однако эта модель не может предсказать смену знака. термоЭДС в литии и благородных металлах, таких как золото и серебро.

Неточности и расширения

Модель свободных электронов имеет несколько недостатков, которые противоречат экспериментальным наблюдениям. Ниже мы перечислим некоторые неточности:

Температурная зависимость

Модель свободных электронов представляет несколько физических величин, которые имеют неверную зависимость от температуры или вообще не зависят, например, электропроводность. Теплопроводность и удельная теплоемкость хорошо прогнозируются для щелочных металлов при низких температурах, но не могут предсказать поведение при высоких температурах, обусловленное движением ионов и рассеянием фононов .

Эффект Холла и магнитосопротивление

Коэффициент Холла имеет постоянное значение R _H = –1/| пе | в модели Друде и в модели свободных электронов. Эта величина не зависит от температуры и силы магнитного поля. Коэффициент Холла на самом деле зависит от зонной структуры , и разница с моделью может быть весьма существенной при изучении таких элементов, как магний и алюминий , которые сильно зависят от магнитного поля. Модель свободных электронов также предсказывает, что поперечное магнитосопротивление, сопротивление в направлении тока, не зависит от силы поля. Почти во всех случаях так и есть.

Направленный

Проводимость некоторых металлов может зависеть от ориентации образца относительно электрического поля. Иногда даже электрический ток не параллелен полю. Эта возможность не описана, поскольку модель не учитывает кристалличность металлов, т.е. существование периодической решетки ионов.

Разнообразие проводимости

Не все материалы являются электрическими проводниками , некоторые не очень хорошо проводят электричество ( изоляторы ), некоторые могут проводить электричество при добавлении примесей, таких как полупроводники . полуметаллы Также существуют с узкими зонами проводимости. Это разнообразие не предсказывается моделью и может быть объяснено только путем анализа валентной зоны и зоны проводимости . Кроме того, электроны не являются единственными носителями заряда в металле: электронные вакансии или дырки можно рассматривать как квазичастицы, несущие положительный электрический заряд. Проводимость дырок приводит к противоположному знаку коэффициентов Холла и Зеебека, предсказываемых моделью.

Другие недостатки присутствуют в законе Видемана-Франца при промежуточных температурах и частотной зависимости металлов в оптическом спектре.

Более точные значения электропроводности и закона Видемана-Франца можно получить, смягчив приближение времени релаксации, обратившись к уравнениям переноса Больцмана .

Обменное взаимодействие полностью исключено из этой модели, и его включение может привести к другим магнитным реакциям, таким как ферромагнетизм .

Непосредственное продолжение модели свободных электронов можно получить, приняв приближение пустой решетки , которое формирует основу модели зонной структуры, известной как модель почти свободных электронов .

Добавление отталкивающих взаимодействий между электронами не сильно меняет представленную здесь картину. Лев Ландау показал, что ферми-газ при отталкивающих взаимодействиях можно рассматривать как газ эквивалентных квазичастиц, слегка изменяющих свойства металла. Модель Ландау теперь известна как теория ферми-жидкости . Более экзотические явления, такие как сверхпроводимость , где взаимодействия могут быть притягательными, требуют более совершенной теории.

См. также

• Теорема Блоха
• Электронная энтропия
• Плотный переплет
• Двумерный электронный газ
• Статистика Бозе – Эйнштейна
• поверхность Ферми
• Белый карлик
• Желе

Ссылки

Цитаты

Ссылки

Общий

• Киттель, Чарльз (1972). Введение в физику твердого тела . Мичиганский университет: Wiley & Sons. ISBN  978-0-471-49024-1 .
• Эшкрофт, Нил ; Мермин, Н. Дэвид (1976). Физика твердого тела . Нью-Йорк: Холт, Райнхарт и Уинстон. ISBN  978-0-03-083993-1 .
• Зоммерфельд, Арнольд ; Бете, Ганс (1933). Электронная теория металлов . Берлин-Гейдельберг: Springer Verlag. ISBN  978-3642950025 .
• Зиман, Дж. М. (1972). Основы теории твердого тела (2-е изд.). Издательство Кембриджского университета. ISBN  0-521-29733-8 .