✖


Jump to content

Фазовый переход

(Перенаправлено из параметра заказа )

На этой диаграмме показана номенклатура различных фазовых переходов.

В физике , химии и других смежных областях, таких как биология, фазовый переход (или фазовый переход ) — это физический процесс перехода между одним состоянием среды в другое. Обычно этот термин используется для обозначения изменений среди основных состояний вещества : твердого , жидкого и газообразного , а в редких случаях — плазмы . Фаза термодинамической системы и состояния вещества обладают одинаковыми физическими свойствами . При фазовом переходе данной среды некоторые свойства среды изменяются в результате изменения внешних условий, например температуры или давления . Это может быть прерывистое изменение; например, жидкость может стать газом при нагревании до точки кипения , что приводит к резкому изменению объема. Выявление внешних условий, при которых происходит превращение, определяет точку фазового перехода.

Виды фазового перехода [ править ]

Состояния материи [ править ]

Упрощенная фазовая диаграмма воды , показывающая, является ли твердый лед, жидкая вода или газообразный водяной пар наиболее стабильным при различных сочетаниях температуры и давления.
См. Также: давление пара и фазовая диаграмма.

Фазовые переходы обычно относятся к переходу вещества из одного из четырех состояний материи в другое. В точке фазового перехода вещества, например при температуре кипения , две участвующие фазы — жидкость и пар — имеют одинаковую свободную энергию и, следовательно, существуют с одинаковой вероятностью. Ниже точки кипения жидкость представляет собой более стабильное состояние из двух, тогда как выше точки кипения газообразная форма является более стабильной.

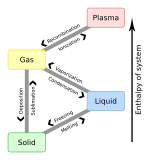
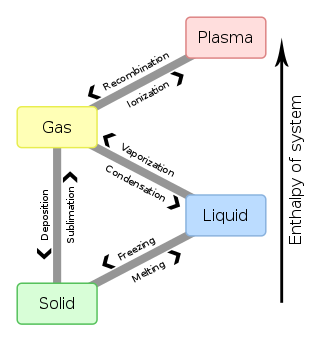
Общие переходы между твердой, жидкой и газообразной фазами одного компонента, вызванные воздействием температуры и/или давления , указаны в следующей таблице:

Фазовые переходы вещества (
)
К
От
Твердый Жидкость Газ Плазма
Твердый
плавление Сублимация
Жидкость Замораживание
Испарение
Газ Депонирование Конденсат
Ионизация
Плазма Рекомбинация

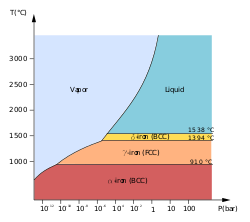
Для одного компонента наиболее стабильная фаза при различных температурах и давлениях может быть показана на фазовой диаграмме . Такая диаграмма обычно изображает состояния в равновесии. Фазовый переход обычно происходит, когда давление или температура изменяются и система переходит из одной области в другую, подобно тому, как вода превращается из жидкого в твердое состояние, как только температура падает ниже точки замерзания . За исключением обычного случая, иногда возможно изменить состояние системы диабатически (в отличие от адиабатически ) таким образом, что ее можно вывести за точку фазового перехода, не испытывая при этом фазового перехода. Полученное состояние является метастабильным , т. е. менее стабильным, чем фаза, в которую произошел бы переход, но и не нестабильным. при перегреве и переохлаждении Это происходит , например, . Метастабильные состояния не появляются на обычных фазовых диаграммах.

Структурный [ править ]

См. Также: Полиморфизм (материаловедение)
Фазовая диаграмма, показывающая аллотропы железа , различающие несколько различных кристаллических структур, включая феррит (α-железо) и аустенит (γ-железо).

Фазовые переходы также могут происходить, когда твердое тело переходит в другую структуру без изменения своего химического состава. У элементов это называется аллотропией , тогда как у соединений — полиморфизмом . Переход от одной кристаллической структуры к другой, от кристаллического твердого тела к аморфному твердому телу или от одной аморфной структуры к другой ( полиаморфы ) — все это примеры фазовых переходов из твердого тела в твердое.

Мартенситное превращение происходит как одно из многих фазовых превращений в углеродистой стали и служит моделью смещающих фазовых превращений . Переходы порядок-беспорядок, такие как в альфа- алюминидах титана . также существуют метастабильные Как и в случае с состояниями вещества, при структурных фазовых переходах фазовые превращения в равновесные. Метастабильный полиморф, который образуется быстро из-за более низкой поверхностной энергии, преобразуется в равновесную фазу при наличии достаточного теплового воздействия для преодоления энергетического барьера.

Магнитный [ править ]

Смотрите также: Магнитная структура
Фазовая диаграмма, показывающая различные магнитные структуры в одной и той же кристаллической структуре моносилицида марганца .

Фазовые переходы также могут описывать смену различных видов магнитного упорядочения . Наиболее известным является переход между ферромагнитной и парамагнитной фазами магнетиков , который происходит в так называемой точке Кюри . Другой пример — переход между разноупорядоченными, соизмеримыми или несоизмеримыми церия магнитными структурами, такими как антимонид . Упрощенная, но очень полезная модель магнитных фазовых переходов представлена ​​моделью Изинга.

Смеси [ править ]

Бинарная фазовая диаграмма, показывающая наиболее стабильные химические соединения титана и никеля при различных соотношениях смешивания и температурах .

Фазовые переходы с участием растворов и смесей более сложны, чем переходы с участием одного соединения. В то время как химически чистые соединения имеют одну температуру плавления между твердой и жидкой фазами, смеси могут либо иметь одну точку плавления, известную как конгруэнтное плавление , либо иметь разные температуры ликвидуса и солидуса, что приводит к температурному диапазону, в котором твердое вещество и жидкость сосуществуют в равновесии. . Это часто имеет место в твердых растворах , где два компонента изоструктурны.

Существует также ряд фазовых переходов, включающих три фазы: эвтектическое превращение, при котором двухкомпонентная однофазная жидкость охлаждается и превращается в две твердые фазы. Тот же процесс, но начинающийся с твердого тела, а не с жидкости, называется эвтектоидным превращением. Перитектическое . превращение, при котором двухкомпонентное однофазное твердое вещество нагревается и превращается в твердую фазу и жидкую фазу Перитектоидная . реакция - это перитектоидная реакция, за исключением того, что в ней участвуют только твердые фазы Монотектическая реакция состоит из перехода от жидкости к комбинации твердого тела и второй жидкости, при этом две жидкости имеют разрыв смешиваемости . [1]

Разделение на несколько фаз может происходить посредством спинодального распада , при котором одна фаза охлаждается и разделяется на два разных состава.

Могут возникнуть неравновесные смеси, например, при пересыщении .

Другие примеры [ править ]

Небольшой кусочек быстро плавящегося твердого аргона демонстрирует два одновременных фазовых перехода. Переход из твердого состояния в жидкость и газа в жидкость (показан белым конденсированным водяным паром).

Другие фазовые изменения включают в себя:

Фазовые переходы происходят, когда термодинамическая свободная энергия системы неаналитична при некотором выборе термодинамических переменных (ср. фазы ). Это состояние обычно возникает из-за взаимодействия большого числа частиц в системе и не возникает в небольших системах. Фазовые переходы могут происходить в нетермодинамических системах, где температура не является параметром. Примеры включают: квантовые фазовые переходы , динамические фазовые переходы и топологические (структурные) фазовые переходы. В системах такого типа вместо температуры используются другие параметры. Например, вероятность соединения заменяет температуру для просачивающихся сетей.

Физика конденсированного состояния
Состояния материи
Фазовые явления
Электронные фазы
Электронные явления
Магнитные фазы
квазичастицы
Мягкая материя
Ученые

Классификации [ править ]

Ehrenfest classification Эренфеста editКлассификация

Пауль Эренфест классифицировал фазовые переходы на основе поведения термодинамической свободной энергии в зависимости от других термодинамических переменных. [5] В этой схеме фазовые переходы обозначались по низшей производной свободной энергии, разрывной при переходе. Фазовые переходы первого рода демонстрируют разрыв первой производной свободной энергии по некоторой термодинамической переменной. [6] Различные переходы твердое тело/жидкость/газ классифицируются как переходы первого рода, поскольку они связаны с прерывистым изменением плотности, которая является (обратной) первой производной свободной энергии по давлению. Фазовые переходы второго рода непрерывны по первой производной ( параметр порядка , который является первой производной свободной энергии по внешнему полю, непрерывен по всему переходу), но демонстрируют разрыв во второй производной свободной энергии. [6] К ним относится ферромагнитный фазовый переход в таких материалах, как железо, где намагниченность , которая является первой производной свободной энергии по отношению к напряженности приложенного магнитного поля, непрерывно увеличивается от нуля по мере того, как температура опускается ниже температуры Кюри . Магнитная восприимчивость , вторая производная свободной энергии по полю, изменяется скачком. Согласно схеме классификации Эренфеста в принципе могут существовать фазовые переходы третьего, четвертого и более высокого порядка. Например, фазовый переход Гросса-Виттена-Вадиа в 2-мерной решеточной квантовой хромодинамике представляет собой фазовый переход третьего рода. [7] [8] Точки Кюри многих ферромагнетиков также представляют собой переход третьего рода, о чем свидетельствует резкое изменение наклона их удельной теплоемкости. [9] [10]

На практике обычно наблюдаются фазовые переходы только первого и второго рода. Фазовый переход второго рода какое-то время вызывал споры, поскольку для точного соприкосновения требуются два листа свободной энергии Гиббса, что настолько маловероятно, что никогда не произойдет на практике. Корнелис Гортер ответил на критику, указав, что поверхность свободной энергии Гиббса может иметь два листа на одной стороне и только один лист на другой стороне, создавая раздвоенный вид. [11] ( [9] стр. 146--150)

Классификация Эренфеста неявно допускает непрерывные фазовые превращения, при которых меняется характер связи материала, но нет разрыва в какой-либо производной свободной энергии. Пример этого происходит на сверхкритических границах жидкость-газ .

Первым примером фазового перехода, не укладывавшегося в классификацию Эренфеста, было точное решение модели Изинга , открытое в 1944 Ларсом Онсагером . Точная теплоемкость отличалась от более ранних приближений среднего поля , которые предсказывали, что она имеет простой разрыв при критической температуре. Вместо этого точная удельная теплоемкость имела логарифмическое расхождение при критической температуре. [12] В последующие десятилетия классификация Эренфеста была заменена упрощенной схемой классификации, способной включать такие переходы.

Современные классификации [ править ]

В современной схеме классификации фазовые переходы разделены на две широкие категории, названные аналогично классам Эренфеста: [5]

Фазовые переходы первого рода — это те, которые связаны со скрытой теплотой . Во время такого перехода система либо поглощает, либо выделяет фиксированное (и обычно большое) количество энергии на объем. Во время этого процесса температура системы будет оставаться постоянной по мере добавления тепла: система находится в «смешанном фазовом режиме», в котором некоторые части системы завершили переход, а другие — нет. [13] [14]

Знакомые примеры — таяние льда или кипение воды (вода не мгновенно превращается в пар , а образует турбулентную смесь жидкой воды и пузырьков пара). Йозеф Имри и Майкл Уортис показали, что подавленное расстройство может расширить переход первого рода. То есть превращение завершается в конечном диапазоне температур, но такие явления, как переохлаждение и перегрев, сохраняются, а при термоциклировании наблюдается гистерезис. [15] [16] [17]

второго рода Фазовые переходы также называют «непрерывными фазовыми переходами» . Они характеризуются дивергентной восприимчивостью, бесконечной корреляционной длиной и степенным затуханием корреляций вблизи критичности . Примерами фазовых переходов второго рода являются ферромагнитный переход, сверхпроводящий переход (для сверхпроводника I рода фазовый переход второго рода при нулевом внешнем поле, а для сверхпроводника II рода фазовый переход второго рода как для нормального, так и для нормального типа). переходы «состояние–смешанное состояние» и «смешанное состояние–сверхпроводящее состояние») и сверхтекучий переход. В отличие от вязкости, тепловое расширение и теплоемкость аморфных материалов быстро изменяются при температуре стеклования. [18] что обеспечивает точное обнаружение с помощью измерений дифференциальной сканирующей калориметрии . Лев Ландау дал феноменологическую теорию фазовых переходов второго рода.

Помимо изолированных простых фазовых переходов, существуют линии перехода, а также мультикритические точки при изменении внешних параметров, таких как магнитное поле или состав.

Некоторые переходы известны как фазовые переходы бесконечного порядка .Они непрерывны, но не нарушают симметрии . Самый известный пример — переход Костерлица–Таулесса в двумерной модели XY . К этому классу относятся многие квантовые фазовые переходы , например в двумерных электронных газах .

Переход жидкость –стекло наблюдается во многих полимерах и других жидкостях, которые можно переохладить значительно ниже температуры плавления кристаллической фазы. Это нетипично во многих отношениях. Это не переход между основными термодинамическими состояниями: широко распространено мнение, что истинное основное состояние всегда является кристаллическим. Стекло представляет собой закаленное неупорядоченное состояние, и его энтропия, плотность и т. д. зависят от термической истории. Поэтому стеклование представляет собой прежде всего динамическое явление: при охлаждении жидкости внутренние степени свободы последовательно выходят из равновесия. Некоторые теоретические методы предсказывают основной фазовый переход в гипотетическом пределе бесконечно больших времен релаксации. [19] [20] Никакие прямые экспериментальные доказательства не подтверждают существование этих переходов.

Характеристические свойства [ править ]

Сосуществование фаз [ править ]

Беспорядочно-уширенный переход первого рода происходит в конечном диапазоне температур, в котором доля низкотемпературной равновесной фазы возрастает от нуля до единицы (100%) при понижении температуры. Это непрерывное изменение сосуществующих фракций в зависимости от температуры открыло интересные возможности. При охлаждении некоторые жидкости превращаются в стекло, а не переходят в равновесную кристаллическую фазу. Это происходит, если скорость охлаждения превышает критическую скорость охлаждения, и объясняется тем, что молекулярные движения становятся настолько медленными, что молекулы не могут перестроиться в кристаллические положения. [21] Это замедление происходит ниже температуры стеклования T g , которая может зависеть от приложенного давления. [18] [22] Если переход замерзания первого рода происходит в определенном диапазоне температур и T g попадает в этот диапазон, то существует интересная возможность того, что переход останавливается, когда он является частичным и неполным. Распространение этих идей на магнитные переходы первого рода, задерживаемые при низких температурах, привело к наблюдению неполных магнитных переходов с сосуществованием двух магнитных фаз вплоть до самой низкой температуры. Впервые сообщалось о переходе из ферромагнитного в антиферромагнитное состояние. [23] о таком постоянном сосуществовании фаз теперь сообщалось при различных магнитных переходах первого рода. К ним относятся манганитовые материалы с колоссальным магнитосопротивлением, [24] [25] магнитокалорические материалы, [26] магнитные материалы с памятью формы, [27] и другие материалы. [28] Интересной особенностью этих наблюдений Tg , попадающих в диапазон температур, в котором происходит переход, является то, что на магнитный переход первого рода влияет магнитное поле, так же как на структурный переход влияет давление. Относительная легкость, с которой можно контролировать магнитные поля, в отличие от давления, открывает возможность исчерпывающего изучения взаимодействия между g и T c . T Сосуществование фаз магнитных переходов первого рода позволит решить нерешенные вопросы в понимании стекол.

Критические точки [ править ]

В любой системе, содержащей жидкую и газообразную фазы, существует особое сочетание давления и температуры, известное как критическая точка , при которой переход между жидкостью и газом становится переходом второго рода. Вблизи критической точки жидкость настолько горячая и сжатая, что различия между жидкой и газообразной фазами практически не существует. Это связано с явлением критической опалесценции — молочного цвета жидкости из-за колебаний плотности на всех возможных длинах волн (в том числе видимого света).

Симметрия [ править ]

Фазовые переходы часто включают процесс нарушения симметрии . Например, охлаждение жидкости до кристаллического твердого тела нарушает непрерывную трансляционную симметрию : каждая точка жидкости имеет одинаковые свойства, но каждая точка кристалла не имеет одинаковых свойств (если только точки не выбраны из узлов решетки кристаллическая решетка). Обычно высокотемпературная фаза содержит больше симметрий, чем низкотемпературная фаза, из-за спонтанного нарушения симметрии , за исключением некоторых случайных симметрий (например, образования тяжелых виртуальных частиц , которое происходит только при низких температурах). [29]

Параметры заказа [ править ]

Параметр порядка — это мера степени порядка на границах системы фазового перехода; обычно он находится в диапазоне от нуля в одной фазе (обычно выше критической точки) до ненулевого значения в другой. [30] В критической точке восприимчивость параметра порядка обычно расходится.

Примером параметра порядка является суммарная намагниченность в ферромагнитной системе, претерпевающей фазовый переход. Для переходов жидкость/газ параметром порядка является разность плотностей.

С теоретической точки зрения параметры порядка возникают в результате нарушения симметрии. Когда это происходит, необходимо ввести одну или несколько дополнительных переменных для описания состояния системы. Например, в ферромагнитной фазе необходимо обеспечить результирующую намагниченность , направление которой было выбрано самопроизвольно при охлаждении системы ниже точки Кюри . Однако обратите внимание, что параметры порядка также могут быть определены для переходов, не нарушающих симметрию. [ нужна ссылка ]

Некоторые фазовые переходы, такие как сверхпроводящий и ферромагнитный, могут иметь параметры порядка более чем для одной степени свободы. В таких фазах параметр порядка может принимать форму комплексного числа, вектора или даже тензора, величина которого при фазовом переходе обращается в нуль. [ нужна ссылка ]

Существуют также двойственные описания фазовых переходов в терминах параметров беспорядка. Они указывают на наличие линейных возбуждений типа вихревых или дефектных линий.

в космологии Актуальность ​

Фазовые переходы, нарушающие симметрию, играют важную роль в космологии . По мере того как Вселенная расширялась и охлаждалась, вакуум претерпел серию фазовых переходов, нарушающих симметрию. Например, электрослабый переход нарушил симметрию SU (2) × U (1) электрослабого поля на симметрию U (1) современного электромагнитного поля . Этот переход важен для объяснения асимметрии между количеством материи и антиматерии в современной Вселенной, согласно теории электрослабого бариогенеза .

Прогрессивные фазовые переходы в расширяющейся Вселенной участвуют в развитии порядка во Вселенной, как это иллюстрирует работа Эрика Чессона. [31] и Дэвид Лайзер . [32]

См. также теории реляционного порядка и порядок и беспорядок .

и классы Критические универсальности показатели

Основная статья: критический показатель

Непрерывные фазовые переходы легче изучать, чем переходы первого рода, из-за отсутствия скрытой теплоты , и было обнаружено, что они обладают многими интересными свойствами. Явления, связанные с непрерывными фазовыми переходами, называются критическими явлениями из-за их связи с критическими точками.

Непрерывные фазовые переходы можно охарактеризовать параметрами, известными как критические показатели . Самым важным из них, пожалуй, является показатель степени, описывающий расхождение длины тепловой корреляции при приближении к переходу. Рассмотрим, например, поведение теплоемкости вблизи такого перехода. Мы варьируем температуру Т системы, сохраняя при этом все остальные термодинамические переменные фиксированными, и обнаруживаем, что переход происходит при некоторой критической Тс температуре . Когда T близок к T c , теплоемкость C обычно имеет степенной закон :

Такое поведение теплоемкости аморфных материалов наблюдается вблизи температуры стеклования, когда универсальный критический показатель α = 0,59. [33] Аналогичное поведение, но с показателем степени ν вместо α , применимо и к длине корреляции.

Показатель степени ν положителен. Это отличается от α . Его фактическое значение зависит от типа рассматриваемого нами фазового перехода.

Критические показатели не обязательно одинаковы выше и ниже критической температуры. Когда непрерывная симметрия явно разбивается на дискретную симметрию с помощью нерелевантной (в смысле ренормгруппы) анизотропии, тогда некоторые показатели степени (например, , показатель восприимчивости) не тождественны. [34]

При −1 < α < 0 теплоемкость имеет «излом» при температуре перехода. Так ведет себя жидкий гелий при лямбда-переходе из нормального состояния в сверхтекучее состояние, для которого эксперименты установили α = −0,013 ± 0,003.По крайней мере, один эксперимент был проведен в условиях невесомости на орбитальном спутнике, чтобы минимизировать перепады давления в образце. [35] Это экспериментальное значение α согласуется с теоретическими предсказаниями, основанными на вариационной теории возмущений . [36]

При 0 < α < 1 теплоемкость расходится при температуре перехода (хотя, поскольку α < 1, энтальпия остается конечной). Примером такого поведения является трехмерный ферромагнитный фазовый переход. В трехмерной модели Изинга для одноосных магнетиков детальные теоретические исследования дали показатель степени α ≈ +0,110.

Некоторые модельные системы не подчиняются степенному закону поведения. Например, теория среднего поля предсказывает конечный разрыв теплоемкости при температуре перехода, а двумерная модель Изинга имеет логарифмическую расходимость. Однако эти системы являются предельными случаями и исключением из правил. Реальные фазовые переходы имеют степенной характер.

Определены несколько других критических показателей β , γ , δ , ν и η , исследующих степенное поведение измеримой физической величины вблизи фазового перехода. Экспоненты связаны масштабными соотношениями, такими как

Можно показать, что существует только два независимых показателя степени, например ν и η .

Примечательно, что фазовые переходы, возникающие в разных системах, часто имеют один и тот же набор критических показателей. Это явление известно как универсальность . Например, было обнаружено, что критические показатели в критической точке жидкость-газ не зависят от химического состава жидкости.

Еще более впечатляюще, но понятно из вышесказанного, они точно соответствуют критическим показателям ферромагнитного фазового перехода в одноосных магнетиках. Говорят, что такие системы относятся к одному классу универсальности. Универсальность - это предсказание теории фазовых переходов ренормгруппы , которая утверждает, что термодинамические свойства системы вблизи фазового перехода зависят только от небольшого числа особенностей, таких как размерность и симметрия, и нечувствительны к основным микроскопическим свойствам система. Опять же, существенным моментом является расхождение длины корреляции.

Критические явления [ править ]

Есть и другие критические явления; например, кроме статических функций существует еще критическая динамика . Как следствие, при фазовом переходе может наблюдаться критическое замедление или ускорение . С предыдущим явлением связано и явление усиленных флуктуаций перед фазовым переходом как следствие меньшей степени устойчивости начальной фазы системы. Большие статические классы универсальности непрерывного фазового перехода распадаются на более мелкие классы динамической универсальности . Помимо критических показателей, существуют также универсальные соотношения для некоторых статических или динамических функций магнитных полей и отклонений температуры от критического значения. [ нужна ссылка ]

Фазовые переходы в биологических системах [ править ]

Фазовые переходы играют важную роль в биологических системах. Примеры включают образование липидного бислоя , переход клубок-глобула в процессе сворачивания белка и плавления ДНК , жидкокристаллические переходы в процессе конденсации ДНК и кооперативное связывание лиганда с ДНК и белками с характером фазового перехода. [37]

В биологических мембранах фазовые переходы из геля в жидкокристаллические играют решающую роль в физиологическом функционировании биомембран. В гелеобразной фазе из-за низкой текучести жирно-ацильных цепей мембранных липидов мембранные белки имеют ограниченное движение и, таким образом, сдерживают выполнение своей физиологической роли. Растения в решающей степени зависят от фотосинтеза хлоропластов тилакоидных мембран , которые подвергаются воздействию низких температур окружающей среды. Мембраны тилакоидов сохраняют врожденную текучесть даже при относительно низких температурах из-за высокой степени жирно-ацильного беспорядка, обеспечиваемого высоким содержанием в них линоленовой кислоты , 18-углеродной цепи с 3-двойными связями. [38] Температуру фазового перехода биологических мембран из геля в кристаллическую жидкость можно определить многими методами, включая калориметрию, флуоресценцию, со спиновой меткой электронный парамагнитный резонанс и ЯМР, путем регистрации измерений соответствующего параметра при ряде температур образца. Предложен также простой метод его определения по интенсивностям линий ЯМР 13 С. [39]

Было высказано предположение, что некоторые биологические системы могут находиться вблизи критических точек. Примеры включают нейронные сети в сетчатке саламандры, [40] птичьи стаи [41] сети экспрессии генов у дрозофилы, [42] и сворачивание белка. [43] Однако неясно, могут ли альтернативные причины объяснить некоторые явления, подтверждающие аргументы в пользу критичности. [44] Было также высказано предположение, что биологические организмы разделяют два ключевых свойства фазовых переходов: изменение макроскопического поведения и когерентность системы в критической точке. [45] Фазовые переходы являются важной особенностью двигательного поведения биологических систем. [46] Спонтанные переходы походки, [47] а также отключение двигательных задач, вызванное усталостью, [48] демонстрируют типичное критическое поведение как намек на внезапное качественное изменение ранее стабильной модели двигательного поведения.

Характерной особенностью фазовых переходов второго рода является появление фракталов в некоторых безмасштабных свойствах. Давно известно, что белковые глобулы формируются в результате взаимодействия с водой. Существует 20 аминокислот, которые образуют боковые группы на пептидных цепях белков, от гидрофильных до гидрофобных, в результате чего первые располагаются вблизи поверхности шара, а вторые — ближе к центру шара. Двадцать фракталов были обнаружены на связанных с растворителем поверхностях более 5000 белковых сегментов. [49] Существование этих фракталов доказывает, что белки функционируют вблизи критических точек фазовых переходов второго рода.

В группах организмов, находящихся в состоянии стресса (при приближении к критическим переходам), корреляции имеют тенденцию к увеличению, но вместе с тем возрастают и колебания. Этот эффект подтверждается многими экспериментами и наблюдениями за группами людей, мышами, деревьями и травянистыми растениями. [50]

Фазовые переходы в социальных системах [ править ]

См. Также: Комплексный системный подход к миру и вооруженным конфликтам § Фазовые переходы

Было высказано предположение, что фазовые переходы происходят в социальных системах, рассматриваемых как динамические системы. Гипотеза, предложенная в 1990-х и 2000-х годах в контексте мира и вооруженных конфликтов, заключается в том, что когда ненасильственный конфликт переходит в фазу вооруженного конфликта, это фазовый переход от скрытых фаз к явным внутри динамической системы. [51] : 49 

Экспериментальный [ править ]

Для изучения различных эффектов применяются различные методы. Избранные примеры:

См. также [ править ]

Ссылки [ править ]

  1. ^ Аскеланд, Дональд Р.; Хэддлтон, Фрэнк; Грин, Фил; Робертсон, Ховард (1996). Наука и инженерия материалов . Чепмен и Холл. п. 286. ИСБН  978-0-412-53910-7 .
  2. ^ Рыбин, М.В.; и др. (2015). «Фазовая диаграмма перехода от фотонных кристаллов к диэлектрическим метаматериалам» . Природные коммуникации . 6 : 10102. arXiv : 1507.08901 . Бибкод : 2015NatCo...610102R . дои : 10.1038/ncomms10102 . ПМК   4686770 . ПМИД   26626302 .
  3. ^ Ред. Чжоу В. и Фань. С. Полупроводники и полуметаллы. Том 100. Фотонно-кристаллическая метаповерхность, оптоэлектроника , Elsevier, 2019.
  4. ^ Кэрол Кендалл (2004). «Основы геохимии стабильных изотопов» . Геологическая служба США . Проверено 10 апреля 2014 г.
  5. ↑ Перейти обратно: Перейти обратно: а б Джагер, Грегг (1 мая 1998 г.). «Классификация фазовых переходов Эренфеста: введение и эволюция». Архив истории точных наук . 53 (1): 51–81. дои : 10.1007/s004070050021 . S2CID   121525126 .
  6. ↑ Перейти обратно: Перейти обратно: а б Бланделл, Стивен Дж.; Кэтрин М. Бланделл (2008). Понятия теплофизики . Издательство Оксфордского университета. ISBN  978-0-19-856770-7 .
  7. ^ Гросс, Дэвид Дж. (1980), «Возможный фазовый переход третьего рода в калибровочной теории большой N-решетки», Physical Review D , 21 (2): 446–453, doi : 10.1103/PhysRevD.21.446
  8. ^ Маджумдар, Сатья Н; Шер, Грегори (31 января 2014 г.). «Верхнее собственное значение случайной матрицы: большие уклонения и фазовый переход третьего рода» . Журнал статистической механики: теория и эксперимент . 2014 (1): P01012. arXiv : 1311.0580 . Бибкод : 2014JSMTE..01..012M . дои : 10.1088/1742-5468/2014/01/P01012 . ISSN   1742-5468 . S2CID   119122520 .
  9. ↑ Перейти обратно: Перейти обратно: а б Пиппард, Альфред Б. (1981). Элементы классической термодинамики: для продвинутых студентов-физиков (Ред.). Кембридж: Univ. Пр. стр. 140–141. ISBN  978-0-521-09101-5 .
  10. ^ Остин, Дж. Б. (ноябрь 1932 г.). «Теплоемкость железа - обзор». Промышленная и инженерная химия . 24 (11): 1225–1235. дои : 10.1021/ie50275a006 . ISSN   0019-7866 .
  11. ^ Джагер, Грегг (1 мая 1998 г.). «Классификация фазовых переходов Эренфеста: введение и эволюция» . Архив истории точных наук . 53 (1): 51–81. дои : 10.1007/s004070050021 . ISSN   1432-0657 .
  12. ^ Стэнли, Х. Юджин (1971). Введение в фазовые переходы и критические явления . Оксфорд: Кларендон Пресс.
  13. ^ Фагри, А., и Чжан, Ю., Явления переноса в многофазных системах , Elsevier, Берлингтон, Массачусетс, 2006,
  14. ^ Фагри А. и Чжан Ю. Основы многофазной теплопередачи и потока , Спрингер, Нью-Йорк, Нью-Йорк, 2020 г.
  15. ^ Имри, Ю.; Уортис, М. (1979). «Влияние закаленных примесей на фазовые переходы первого рода». Физ. Преподобный Б. 19 (7): 3580–3585. Бибкод : 1979PhRvB..19.3580I . дои : 10.1103/physrevb.19.3580 .
  16. ^ Кумар, Кранти; Праманик, АК; Банерджи, А.; Чада, П.; Рой, SB; Парк, С.; Чжан, CL; Чеонг, С.-В. (2006). «Относительно переохлаждения и стеклоподобного прекращения кинетики для систем с разделенными фазами: DopedCeFe2 и (La, Pr, Ca) MnO3». Физический обзор B . 73 (18): 184435. arXiv : cond-mat/0602627 . Бибкод : 2006PhRvB..73r4435K . дои : 10.1103/PhysRevB.73.184435 . ISSN   1098-0121 . S2CID   117080049 .
  17. ^ Пасквини, Дж.; Дарока, Д. Перес; Чилиотт, К.; Лозано, Г.С.; Бекерис, В. (2008). «Упорядоченные, неупорядоченные и сосуществующие стабильные вихревые решетки в монокристаллах NbSe2». Письма о физических отзывах . 100 (24): 247003. arXiv : 0803.0307 . Бибкод : 2008PhRvL.100x7003P . doi : 10.1103/PhysRevLett.100.247003 . ISSN   0031-9007 . ПМИД   18643617 . S2CID   1568288 .
  18. ↑ Перейти обратно: Перейти обратно: а б Оджован, Мичиган (2013). «Упорядочение и структурные изменения при переходе стекло-жидкость». Дж. Некристаллический. Твердые тела . 382 : 79–86. Бибкод : 2013JNCS..382...79O . дои : 10.1016/j.jnoncrysol.2013.10.016 .
  19. ^ Гоце, Вольфганг. «Сложная динамика стеклообразующих жидкостей: теория связи мод».
  20. ^ Лубченко, В. Волынес; Волинс, Питер Г. (2007). «Теория структурных стекол и переохлажденных жидкостей». Ежегодный обзор физической химии . 58 : 235–266. arXiv : cond-mat/0607349 . Бибкод : 2007ARPC...58..235L . doi : 10.1146/annurev.physchem.58.032806.104653 . ПМИД   17067282 . S2CID   46089564 .
  21. ^ Грир, Ал. (1995). «Металлические стаканы». Наука . 267 (5206): 1947–1953. Бибкод : 1995Sci...267.1947G . дои : 10.1126/science.267.5206.1947 . ПМИД   17770105 . S2CID   220105648 .
  22. ^ Тарьюс, Г. (2007). «Материаловедение: Металл превратился в стекло» . Природа . 448 (7155): 758–759. Бибкод : 2007Natur.448..758T . дои : 10.1038/448758a . ПМИД   17700684 . S2CID   4410586 .
  23. ^ Манекар, Массачусетс; Чаудхари, С.; Чаттопадхай, МК; Сингх, К.Дж.; Рой, SB; Чадда, П. (2001). «Переход первого рода от антиферромагнетизма к ферромагнетизму в Ce(Fe 0,96 Al 0,04 ) 2 ». Физический обзор B . 64 (10): 104416. arXiv : cond-mat/0012472 . Бибкод : 2001PhRvB..64j4416M . дои : 10.1103/PhysRevB.64.104416 . ISSN   0163-1829 . S2CID   16851501 .
  24. ^ Банерджи, А.; Праманик, АК; Кумар, Кранти; Чадда, П. (2006). «Сосуществующие перестраиваемые фракции стеклообразных и равновесных фаз дальнего порядка в манганитах». Физический журнал: конденсированное вещество . 18 (49): Л605. arXiv : cond-mat/0611152 . Бибкод : 2006JPCM...18L.605B . дои : 10.1088/0953-8984/18/49/L02 . S2CID   98145553 .
  25. ^ У В.; Израиль К.; Хур Н.; Парк С.; Чонг SW; де Лозанн А. (2006). «Магнитная визуализация переохлажденного стеклования в слабонеупорядоченном ферромагнетике». Природные материалы . 5 (11): 881–886. Бибкод : 2006NatMa...5..881W . дои : 10.1038/nmat1743 . ПМИД   17028576 . S2CID   9036412 .
  26. ^ Рой, SB; Чаттопадхай, МК; Чада, П.; Мур, доктор медицинских наук; Перкинс, ГК; Коэн, Л.Ф.; Гшнейднер, К.А.; Печарский, В.К. (2006). «Свидетельства состояния магнитного стекла в магнитокалорическом материале Gd 5 Ge 4 ». Физический обзор B . 74 (1): 012403. Бибкод : 2006PhRvB..74a2403R . дои : 10.1103/PhysRevB.74.012403 . ISSN   1098-0121 .
  27. ^ Лахани, Арчана; Банерджи, А.; Чада, П.; Чен, X.; Рамануджан, Р.В. (2012). «Магнитное стекло из сплава с памятью формы: Ni 45 Co 5 Mn 38 Sn 12 ». Физический журнал: конденсированное вещество . 24 (38): 386004. arXiv : 1206.2024 . Бибкод : 2012JPCM...24L6004L . дои : 10.1088/0953-8984/24/38/386004 . ISSN   0953-8984 . ПМИД   22927562 . S2CID   206037831 .
  28. ^ Кушваха, Паллави; Лахани, Арчана; Рават, Р.; Чадда, П. (2009). «Низкотемпературное исследование индуцированного полем перехода антиферромагнит-ферромагнитный в Fe-Rh, легированном Pd». Физический обзор B . 80 (17): 174413. arXiv : 0911.4552 . Бибкод : 2009PhRvB..80q4413K . дои : 10.1103/PhysRevB.80.174413 . ISSN   1098-0121 . S2CID   119165221 .
  29. ^ Иванцевич, Владимир Г.; Иванцевич, Тиджиана, Т. (2008). Комплексная нелинейность . Берлин: Шпрингер. стр. 176–177. ISBN  978-3-540-79357-1 . Проверено 12 октября 2014 г. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
  30. ^ Кларк, Дж. Б.; Хасти, JW; Кильборг, LHE; Метселаар, Р.; Теккерей, ММ (1994). «Определения терминов, относящихся к фазовым переходам твердого тела» . Чистая и прикладная химия . 66 (3): 577–594. дои : 10.1351/pac199466030577 . S2CID   95616565 .
  31. ^ Чессон, Эрик Дж. (2001). Космическая Эволюция . Издательство Гарвардского университета. ISBN  978-0-674-00342-2 .
  32. ^ Дэвид Лайзер, Космогенез, Развитие порядка во Вселенной , Оксфордский университет. Пресс, 1991 г.
  33. ^ Оджован, Майкл И.; Ли, Уильям Э. (2006). «Топологически неупорядоченные системы при стекловании» (PDF) . Физический журнал: конденсированное вещество . 18 (50): 11507–11520. Бибкод : 2006JPCM...1811507O . дои : 10.1088/0953-8984/18/50/007 . S2CID   96326822 .
  34. ^ Леонард, Ф.; Деламотт, Б. (2015). «Критические показатели могут быть разными по обе стороны перехода». Физ. Преподобный Летт . 115 (20): 200601. arXiv : 1508.07852 . Бибкод : 2015PhRvL.115t0601L . doi : 10.1103/PhysRevLett.115.200601 . ПМИД   26613426 . S2CID   22181730 .
  35. ^ Липа, Дж.; Ниссен, Дж.; Стрикер, Д.; Суонсон, Д.; Чуй, Т. (2003). «Удельная теплоемкость жидкого гелия в невесомости очень близко к лямбда-точке». Физический обзор B . 68 (17): 174518. arXiv : cond-mat/0310163 . Бибкод : 2003PhRvB..68q4518L . дои : 10.1103/PhysRevB.68.174518 . S2CID   55646571 .
  36. ^ Кляйнерт, Хаген (1999). «Критические показатели семипетлевой теории сильной связи φ4 в трех измерениях». Физический обзор D . 60 (8): 085001. arXiv : hep-th/9812197 . Бибкод : 1999ФРвД..60х5001К . doi : 10.1103/PhysRevD.60.085001 . S2CID   117436273 .
  37. ^ Д.Ю. Ландо и В.Б. Тейф (2000). «Дальнодействующие взаимодействия между лигандами, связанными с молекулой ДНК, приводят к адсорбции с характером фазового перехода первого рода». Дж. Биомол. Структура. Дин . 17 (5): 903–911. дои : 10.1080/07391102.2000.10506578 . ПМИД   10798534 . S2CID   23837885 .
  38. ^ Яшрой Р.Ц. (1987). " 13 Исследование ЯМР липидов липидных жирных ацильных цепей мембран хлоропластов» . Индийский журнал биохимии и биофизики . 24 (6): 177–178. doi : 10.1016/0165-022X(91)90019-S . PMID   3428918 .
  39. ^ ЯшРой, RC (1990). «Определение температуры фазового перехода мембранных липидов по интенсивностям ЯМР 13-С» . Журнал биохимических и биофизических методов . 20 (4): 353–356. дои : 10.1016/0165-022X(90)90097-V . ПМИД   2365951 .
  40. ^ Ткачик, Гаспер; Мора, Тьерри; Марре, Оливье; Амодей, Дарио; Берри II, Майкл Дж.; Бялек, Уильям (2014). «Термодинамика сети нейронов: признаки критичности». arXiv : 1407.5946 [ q-bio.NC ].
  41. ^ Бялек, В; Каванья, А; Джардина, Я (2014). «Социальные взаимодействия доминируют в контроле скорости при уравновешивании естественных стад на грани критического состояния» . ПНАС . 111 (20): 7212–7217. arXiv : 1307.5563 . Бибкод : 2014PNAS..111.7212B . дои : 10.1073/pnas.1324045111 . ПМК   4034227 . ПМИД   24785504 .
  42. ^ Кротов, Д; Дюбюи, ЖО; Грегор, Т; Бялек, Вт (2014). «Морфогенез в критическом состоянии» . ПНАС . 111 (10): 3683–3688. arXiv : 1309.2614 . Бибкод : 2014PNAS..111.3683K . дои : 10.1073/pnas.1324186111 . ПМЦ   3956198 . ПМИД   24516161 .
  43. ^ Мора, Тьерри; Бялек, Уильям (2011). «Находятся ли биологические системы на критическом уровне?». Журнал статистической физики . 144 (2): 268–302. arXiv : 1012.2242 . Бибкод : 2011JSP...144..268M . дои : 10.1007/s10955-011-0229-4 . S2CID   703231 .
  44. ^ Шваб, Дэвид Дж; Неменман, Илья; Мехта, Панкадж (2014). «Закон Ципфа и критичность в многомерных данных без тонкой настройки» . Письма о физических отзывах . 113 (6): 068102. arXiv : 1310.0448 . Бибкод : 2014PhRvL.113f8102S . doi : 10.1103/PhysRevLett.113.068102 . ПМК   5142845 . ПМИД   25148352 .
  45. ^ Лонго, Г.; Монтевиль, М. (1 августа 2011 г.). «От физики к биологии путем расширения критичности и нарушений симметрии» . Прогресс биофизики и молекулярной биологии . Системная биология и рак. 106 (2): 340–347. arXiv : 1103.1833 . doi : 10.1016/j.pbiomolbio.2011.03.005 . ПМИД   21419157 . S2CID   723820 .
  46. ^ Келсо, Дж. А. Скотт (1995). Динамические паттерны: самоорганизация мозга и поведения (сложные адаптивные системы) . МТИ Пресс. ISBN  978-0-262-61131-2 .
  47. ^ Дидрих, Ф.Дж.; Уоррен, WH младший (1995). «Зачем менять походку? Динамика перехода ходьба-бег». Журнал экспериментальной психологии. Человеческое восприятие и производительность . 21 (1): 183–202. дои : 10.1037/0096-1523.21.1.183 . ПМИД   7707029 .
  48. ^ Христовский Р.; Балаге, Н. (2010). «Точка спонтанного прекращения, вызванная усталостью - неравновесные фазовые переходы и критическое поведение при квазиизометрическом напряжении». Наука о движении человека . 29 (4): 483–493. дои : 10.1016/j.humov.2010.05.004 . ПМИД   20619908 .
  49. ^ Море, Марсело; Зебенде, Гилни (январь 2007 г.). «Гидрофобность аминокислот и доступная площадь поверхности». Физический обзор E . 75 (1): 011920. Бибкод : 2007PhRvE..75a1920M . дои : 10.1103/PhysRevE.75.011920 . ПМИД   17358197 .
  50. ^ Горбань, АН; Смирнова Е.В.; Тюкина Т.А. (август 2010 г.). «Корреляции, риск и кризис: от физиологии к финансам» . Физика А: Статистическая механика и ее приложения . 389 (16): 3193–3217. arXiv : 0905.0129 . Бибкод : 2010PhyA..389.3193G . дои : 10.1016/j.physa.2010.03.035 . S2CID   276956 .
  51. ^ Дайан Хендрик (июнь 2009 г.), Теория сложности и трансформация конфликтов: исследование потенциала и последствий (PDF) , Департамент исследований проблем мира, Брэдфордский университет , Wikidata   Q126669745 , заархивировано (PDF) из оригинала 26 ноября 2022 г.

Дальнейшее чтение [ править ]

Внешние ссылки [ править ]

Викискладе есть медиафайлы, связанные с фазовыми изменениями .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Phase_transition&oldid=1233012087#Order_parameters"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 6f494b5e64f19b8feab6a3d83dac4e45__1720286820
URL1:https://arc.ask3.ru/arc/aa/6f/45/6f494b5e64f19b8feab6a3d83dac4e45.html
Заголовок, (Title) документа по адресу, URL1:
Phase transition - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)