Спинодаль

Фазовая диаграмма, отображающая спинодальные кривые внутри бинодальных кривых сосуществования и две критические точки : верхнюю и нижнюю критическую температуру раствора .

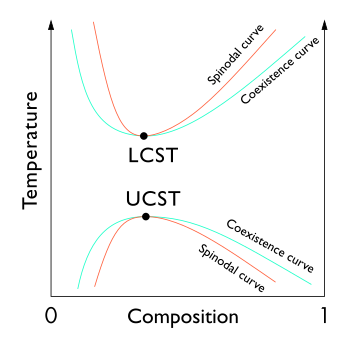
В термодинамике предел локальной устойчивости к расслоению фаз относительно малых флуктуаций четко определяется условием, что вторая производная равна свободной энергии Гиббса нулю.

${\operatorname {d} ^{2}\!G \over \operatorname {d} \!x^{2}}{=}0$

Геометрическое положение этих точек (точка перегиба внутри кривой Gx или Gc, свободная энергия Гиббса как функция состава ) известна как спинодальная кривая. Для составов внутри этой кривой бесконечно малые колебания состава и плотности приведут к разделению фаз посредством спинодального распада . Вне кривой решение будет как минимум метастабильным по отношению к флуктуациям. Другими словами, за пределами спинодальной кривой в результате осторожного процесса можно получить однофазную систему. Внутри него только процессы, далекие от термодинамического равновесия , такие как физическое осаждение из паровой фазы , позволят получать однофазные композиции. Локальные точки сосуществующих составов, определяемые общей конструкцией касательной, известны как бинодальная кривая сосуществования , которая обозначает состояние равновесия системы с минимальной энергией. Повышение температуры приводит к уменьшению разницы между энтропией смешения и энтальпией смешения, и, таким образом, сосуществующие составы сближаются. Бинодальная кривая составляет основу разрыва смешиваемости на фазовой диаграмме. Свободная энергия смешения меняется в зависимости от температуры и концентрации, а бинодали и спинодали встречаются при критической или устойчивой температуре и составе.

Критерий

Для бинарных растворов термодинамическим критерием, определяющим спинодальную кривую, является то, что вторая производная свободной энергии по плотности или некоторой переменной состава равна нулю.

Критическая точка

Экстремумы спинодали на графике зависимости температуры от состава совпадают с экстремумами бинодали и известны как критические точки . Саму спинодаль можно рассматривать как линию псевдокритических точек, при этом корреляционная функция принимает масштабирующую форму с неклассическими критическими показателями . Строго говоря, спинодаль определяется как объект теории среднего поля . Как таковая спинодаль не существует в реальных системах. но можно экстраполировать и сделать вывод о существовании псевдоспинодали, которая демонстрирует критическое поведение, такое как критическое замедление .

Изотермические равновесия жидкость-жидкость

В случае тройного изотермического равновесия жидкость-жидкость спинодальная кривая (полученная из матрицы Гессе) и соответствующая критическая точка могут использоваться для облегчения процесса корреляции экспериментальных данных.