Жидкость

Жидкость . — это почти несжимаемая жидкость , которая принимает форму сосуда, но сохраняет почти постоянный объем, не зависящий от давления Это одно из четырех фундаментальных состояний материи (остальные — твердое тело , газ и плазма ) и единственное состояние с определенным объемом, но не фиксированной формой.

Плотность жидкости обычно близка к плотности твердого тела и значительно выше плотности газа. Поэтому жидкость и твердое вещество называются конденсированным веществом . С другой стороны, поскольку жидкости и газы обладают общей способностью течь, их называют жидкостями.

Жидкость состоит из мельчайших колеблющихся частиц материи, например атомов, скрепленных межмолекулярными связями . Как и газ, жидкость способна течь и принимать форму сосуда. В отличие от газа жидкость сохраняет довольно постоянную плотность и не рассеивается, заполняя все пространство контейнера.

Хотя на Земле много жидкой воды, это состояние материи на самом деле наименее распространено в известной Вселенной, поскольку для существования жидкостей требуется относительно узкий диапазон температуры/давления. Самая известная материя во Вселенной — это либо газ (как межзвездные облака ), либо плазма (как звезды ).

Введение

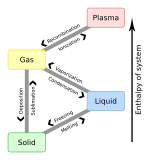
Жидкость — одно из четырех основных состояний материи , остальные — твердое тело, газ и плазма . Жидкость есть жидкость . В отличие от твердого тела, молекулы жидкости обладают гораздо большей свободой движения. Силы, которые связывают молекулы вместе в твердом теле, в жидкости носят временный характер, позволяя жидкости течь, в то время как твердое тело остается твердым.

Жидкость, как и газ, проявляет свойства жидкости. Жидкость может течь, принимать форму контейнера и, если ее поместить в герметичный контейнер, равномерно распределять приложенное давление по каждой поверхности контейнера. Если жидкость поместить в пакет, ей можно придать любую форму. В отличие от газа, жидкость практически несжимаема, а это означает, что она занимает почти постоянный объем в широком диапазоне давлений; Обычно он не расширяется, чтобы заполнить доступное пространство в контейнере, а образует собственную поверхность и не всегда может легко смешиваться с другой жидкостью. Эти свойства делают жидкость подходящей для таких применений, как гидравлика .

Частицы жидкости связаны прочно, но не жестко. Они способны свободно перемещаться друг вокруг друга, что приводит к ограниченной степени подвижности частиц. По мере повышения температуры усиление колебаний молекул приводит к увеличению расстояний между молекулами. Когда жидкость достигает точки кипения , силы сцепления, тесно связывающие молекулы, разрушаются, и жидкость переходит в газообразное состояние (если не происходит перегрева ). При понижении температуры расстояния между молекулами становятся меньше. Когда жидкость достигает точки замерзания, молекулы обычно образуют очень специфический порядок, называемый кристаллизацией, и связи между ними становятся более жесткими, переводя жидкость в твердое состояние (если не происходит переохлаждения ).

Примеры

Только два элемента являются жидкими при стандартных условиях по температуре и давлению : ртуть и бром . Еще четыре элемента имеют температуру плавления чуть выше комнатной температуры : франций , цезий , галлий и рубидий . ^[1] Кроме того, некоторые смеси элементов являются жидкими при комнатной температуре, даже если отдельные элементы в тех же условиях являются твердыми (см. Эвтектическая смесь ). Примером может служить металлический сплав натрия и калия NaK . ^[2] Другие металлические сплавы, которые являются жидкими при комнатной температуре, включают галинстан , который представляет собой сплав галлия, индия и олова, который плавится при -19 ° C (-2 ° F), а также некоторые амальгамы (сплавы с участием ртути). ^[3]

К чистым веществам, которые при нормальных условиях являются жидкими, относятся вода, этанол и многие другие органические растворители. Жидкая вода имеет жизненно важное значение в химии и биологии и необходима для всех известных форм жизни. ^[4]^[5]

К неорганическим жидкостям относятся вода, магма , неорганические неводные растворители и многие кислоты .

К важным повседневным жидкостям относятся водные растворы , такие как бытовой отбеливатель , другие смеси различных веществ, такие как минеральное масло и бензин, эмульсии , такие как винегрет или майонез , суспензии, такие как кровь, и коллоиды , такие как краска и молоко .

Многие газы можно сжижать путем охлаждения, получая такие жидкости, как жидкий кислород , жидкий азот , жидкий водород и жидкий гелий . Однако не все газы можно сжижать при атмосферном давлении. Углекислый газ , например, можно сжижать только при давлении выше 5,1 атм . ^[6]

Некоторые материалы не могут быть отнесены к трем классическим состояниям материи. Например, жидкие кристаллы (используемые в жидкокристаллических дисплеях ) обладают свойствами как твердого тела, так и жидкости, и принадлежат к своему собственному состоянию материи, отличному от жидкости или твердого тела. ^[7]

Приложения

Смазка

Жидкости полезны в качестве смазок из-за их способности образовывать тонкий, свободно текущий слой между твердыми материалами. Смазочные материалы, такие как масло, выбираются с учетом характеристик вязкости и текучести, которые подходят для всего диапазона рабочих температур компонента. Масла часто используются в двигателях, коробках передач , металлообработке и гидравлических системах из-за их хороших смазочных свойств. ^[8]

сольватация

Многие жидкости используются в качестве растворителей для растворения других жидкостей или твердых веществ. Решения можно найти в самых разных областях применения, включая краски , герметики и клеи . Нафта и ацетон часто используются в промышленности для очистки деталей и механизмов от масла, смазки и смолы. Жидкости организма представляют собой растворы на водной основе.

Поверхностно-активные вещества обычно содержатся в мыле и моющих средствах . Растворители, такие как спирт, часто используются в качестве противомикробных средств . Они содержатся в косметике, чернилах и лазерах на жидких красителях . Их используют в пищевой промышленности, в таких процессах, как добыча растительного масла . ^[9]

Охлаждение

Жидкости, как правило, имеют лучшую теплопроводность , чем газы, а способность течь делает жидкость подходящей для отвода избыточного тепла от механических компонентов. Тепло можно отводить путем направления жидкости через теплообменник , например, радиатор , или тепло можно отводить вместе с жидкостью во время испарения . ^[10] Водяные или гликолевые охлаждающие жидкости используются для предотвращения перегрева двигателей. ^[11] Теплоносители, используемые в ядерных реакторах, включают воду или жидкие металлы, такие как натрий или висмут . ^[12] Пленки жидкого топлива используются для охлаждения камер тяги ракет . ^[13] При механической обработке вода и масла используются для удаления избыточного тепла, которое может быстро испортить как заготовку, так и инструмент. Во время потоотделения пот отводит тепло от тела человека путем испарения. В промышленности отопления, вентиляции и кондиционирования воздуха (HVAC) жидкости, такие как вода, используются для передачи тепла из одной области в другую. ^[14]

Кулинария

Жидкости часто используются в кулинарии из-за их превосходных свойств теплопередачи. Помимо теплопроводности, жидкости передают энергию посредством конвекции. В частности, поскольку более теплые жидкости расширяются и поднимаются, в то время как более холодные области сжимаются и опускаются, жидкости с низкой кинематической вязкостью имеют тенденцию передавать тепло посредством конвекции при довольно постоянной температуре, что делает жидкость подходящей для бланширования , варки или жарки . Еще более высоких показателей теплопередачи можно достичь за счет конденсации газа в жидкость. При температуре кипения жидкости вся тепловая энергия используется для фазового перехода из жидкости в газ без сопутствующего повышения температуры и сохраняется в виде химической потенциальной энергии . Когда газ конденсируется обратно в жидкость, эта избыточная тепловая энергия высвобождается при постоянной температуре. Это явление используется в таких процессах, как пропаривание .

Дистилляция

Поскольку жидкости часто имеют разные точки кипения, смеси или растворы жидкостей или газов обычно можно разделить путем перегонки с использованием тепла, холода, вакуума , давления или других средств. Дистилляцию можно найти во всем: от производства алкогольных напитков до нефтеперерабатывающих заводов и криогенной перегонки газов, таких как аргон , кислород , азот , неон или ксенон , путем сжижения (охлаждения их ниже температуры их индивидуального кипения). ^[15]

Гидравлика

Жидкость является основным компонентом гидравлических систем, которые используют закон Паскаля для обеспечения гидравлической энергии . Такие устройства, как насосы и водяные колеса, использовались для преобразования движения жидкости в механическую работу с древних времен . Масло подается через гидравлические насосы , которые передают эту силу на гидравлические цилиндры . Гидравлику можно найти во многих приложениях, таких как автомобильные тормоза и трансмиссии , тяжелое оборудование и системы управления самолетами. Различные гидравлические прессы широко применяются в ремонте и производстве, для подъема, прессования, зажима и формовки. ^[16]

Жидкие металлы

Жидкие металлы обладают несколькими свойствами, которые полезны для измерения и срабатывания , в частности, их электропроводность и способность передавать силы (несжимаемость). Будучи свободно текучими веществами, жидкие металлы сохраняют свои объемные свойства даже при сильной деформации. По этой причине их предложили использовать в мягких роботах и носимых медицинских устройствах , которые должны быть способны работать при многократной деформации. ^[17]^[18] Металлический галлий считается многообещающим кандидатом для этих применений, поскольку он представляет собой жидкость при температуре, близкой к комнатной, имеет низкую токсичность и медленно испаряется. ^[19]

Разнообразный

Жидкости иногда используются в измерительных приборах. Термометр , в часто использует тепловое расширение жидкостей, таких как ртуть сочетании с их способностью течь для определения температуры. Манометр давления использует вес жидкости для определения воздуха . ^[20]

Свободная поверхность вращающейся жидкости образует круглый параболоид и поэтому может использоваться как телескоп . Они известны как телескопы с жидкостным зеркалом . ^[21] Они значительно дешевле обычных телескопов, ^[22] но может указывать только прямо вверх ( зенитный телескоп ). Обычно в качестве жидкости выбирают ртуть.

Механические свойства

Объем

Кавитация в воде от гребного винта лодки

Количество жидкостей измеряется в единицах объема . К ним относятся единица СИ кубический метр (м ³) и его делений, в частности кубического дециметра, чаще называемого литром (1 дм ³ = 1 л = 0,001 м ³), а также кубический сантиметр, также называемый миллилитр (1 см ³ = 1 мл = 0,001 л = 10 ⁻⁶ м ³). ^[23]

Объем жидкости определяется ее температурой и давлением . Жидкости обычно расширяются при нагревании и сжимаются при охлаждении. Заметным исключением является вода с температурой от 0 °C до 4 °C. ^[24]

С другой стороны, жидкости обладают небольшой сжимаемостью . Вода, например, сжимается всего на 46,4 части на миллион на каждую единицу увеличения атмосферного давления (бар). ^[25] около 4000 бар (400 мегапаскалей или 58 000 фунтов на квадратный дюйм ) при комнатной температуре объем воды уменьшается только на 11%. При давлении ^[26] Несжимаемость делает жидкости пригодными для передачи гидравлической энергии , поскольку изменение давления в одной точке жидкости передается в неизменном виде на все остальные части жидкости, и при сжатии теряется очень мало энергии. ^[27]

Однако пренебрежимо малая сжимаемость приводит и к другим явлениям. Удары труб, называемые гидравлическим ударом , происходят, когда клапан внезапно закрывается, создавая огромный скачок давления в клапане, который движется назад по системе со скоростью чуть ниже звука. Другое явление, вызванное несжимаемостью жидкости, — кавитация . Поскольку жидкости обладают низкой эластичностью, их можно буквально разорвать на части в местах с высокой турбулентностью или резким изменением направления, например, на задней кромке гребного винта лодки или остром углу трубы. Жидкость в области низкого давления (вакуума) испаряется и образует пузырьки, которые затем схлопываются при попадании в области высокого давления. Это заставляет жидкость заполнять полости, оставленные пузырьками, с огромной локализованной силой, разрушая любую прилегающую твердую поверхность. ^[28]

Давление и плавучесть

В гравитационном поле жидкости оказывают давление на стенки контейнера, а также на все, что находится внутри самой жидкости. Это давление передается во всех направлениях и увеличивается с глубиной. Если жидкость покоится в однородном гравитационном поле, давление $p$ на глубине $z$ дается ^[29]

p=p_{0}+\rho gz\,

где:

p_{0}\,

это давление на поверхности

\rho \,

- плотность жидкости, считающаяся однородной с глубиной

g\,

это гравитационное ускорение

Для водоема, открытого воздуху, $p_{0}$ будет атмосферное давление .

Статические жидкости в однородных гравитационных полях также демонстрируют явление плавучести , когда объекты, погруженные в жидкость, испытывают результирующую силу из-за изменения давления с глубиной. Величина силы равна весу жидкости, вытесненной предметом, а направление силы зависит от средней плотности погруженного предмета. Если плотность меньше плотности жидкости, выталкивающая сила направлена вверх , и объект плавает, тогда как если плотность больше , выталкивающая сила направлена вниз, и объект тонет. Это известно как принцип Архимеда . ^[30]

Поверхности

Если объем жидкости точно не соответствует объему ее сосуда, наблюдается одна или несколько поверхностей. Наличие поверхности приводит к новым явлениям, которых нет в объемной жидкости. Это связано с тем, что молекула на поверхности имеет связи с другими молекулами жидкости только на внутренней стороне поверхности, что подразумевает результирующую силу, тянущую поверхностные молекулы внутрь. Эквивалентно, эту силу можно описать с точки зрения энергии: существует фиксированное количество энергии, связанное с формированием поверхности заданной площади. Эта величина представляет собой свойство материала, называемое поверхностным натяжением , в единицах энергии на единицу площади (единицы СИ: Дж / м) . ²). Жидкости с сильными межмолекулярными силами имеют тенденцию иметь большое поверхностное натяжение. ^[31]

Практическим следствием поверхностного натяжения является то, что жидкости имеют тенденцию минимизировать площадь своей поверхности, образуя сферические капли и пузырьки , если не присутствуют другие ограничения. Поверхностное натяжение также ответственно за ряд других явлений, включая поверхностные волны , капиллярное действие , смачивание и рябь . В жидкостях, находящихся в наноразмерном ограничении , поверхностные эффекты могут играть доминирующую роль, поскольку – по сравнению с макроскопическим образцом жидкости – гораздо большая часть молекул расположена вблизи поверхности.

Поверхностное натяжение жидкости напрямую влияет на ее смачиваемость . Большинство распространенных жидкостей имеют напряженность в десятки мДж/м. ², поэтому капли масла, воды или клея могут легко сливаться и прилипать к другим поверхностям, тогда как жидкие металлы, такие как ртуть, могут иметь напряжение в сотни мДж/м. ²Таким образом, капли не смешиваются легко, и поверхности могут смачиваться только при определенных условиях.

Поверхностное натяжение обычных жидкостей занимает относительно узкий диапазон значений при воздействии изменяющихся условий, таких как температура, что сильно контрастирует с огромными изменениями, наблюдаемыми в других механических свойствах, таких как вязкость. ^[32]

Свободная поверхность жидкости возмущается силой тяжести ( плоскость ) и волнами ( шероховатость поверхности ).

Поток

Моделирование вязкости . Жидкость слева имеет более низкую вязкость и ньютоновское поведение, тогда как жидкость справа имеет более высокую вязкость и неньютоновское поведение.

Важным физическим свойством, характеризующим течение жидкостей, является вязкость . Интуитивно вязкость описывает сопротивление жидкости течению.

С технической точки зрения вязкость измеряет сопротивление жидкости деформации с заданной скоростью, например, когда ее сдвигают с конечной скоростью. ^[33] Конкретным примером является жидкость, текущая черезтруба: в этом случае жидкость испытывает сдвиговую деформацию, поскольку вблизи стенок трубы она течет медленнеечем рядом с центром. В результате он проявляет вязкое сопротивление течению. Чтобы поддерживать поток, необходимо приложить внешнюю силу, например, разницу давлений между концами трубы.

Вязкость жидкостей уменьшается с повышением температуры. ^[34]

Точный контроль вязкости важен во многих областях применения, особенно в смазочной промышленности. Одним из способов достижения такого контроля является смешивание двух или более жидкостей разной вязкости в точных соотношениях. ^[35] Кроме того, существуют различные добавки, которые могут модулировать температурную зависимость.вязкость смазочных масел. Эта возможность важна, поскольку оборудование часто работает в диапазоне температуры (см. также индекс вязкости ). ^[36]

Вязкое поведение жидкости может быть ньютоновским или неньютоновским . Ньютоновская жидкость демонстрирует линейную кривую деформации/напряжения, что означает, что ее вязкость не зависит от времени, скорости сдвига или истории скорости сдвига. Примеры ньютоновских жидкостей включают воду, глицерин , моторное масло , мед или ртуть. Неньютоновская жидкость — это жидкость, вязкость которой не зависит от этих факторов и либо загустевает (вязкость увеличивается), либо разжижается (вязкость уменьшается) под действием сдвига. Примеры неньютоновских жидкостей включают кетчуп , заварной крем или растворы крахмала . ^[37]

Распространение звука

Скорость звука в жидкости определяется выражением $c={\sqrt {K/\rho }}$ где $K$ - объемный модуль жидкости и $\rho$ плотность. Например, вода имеет модуль объемного сжатия около 2,2 ГПа и плотность 1000 кг/м. ³, что дает c = 1,5 км/с. ^[38]

Термодинамика

Фазовые переходы

Типичная фазовая диаграмма . Пунктирная линия показывает аномальное поведение воды. Зеленые линии показывают, как температура замерзания может меняться в зависимости от давления, а синяя линия показывает, как температура кипения может меняться в зависимости от давления. Красная линия показывает границу, где может происходить сублимация или осаждение .

При температуре ниже точки кипения любое вещество в жидкой форме будет испаряться до достижения равновесия с обратным процессом конденсации его паров. В этот момент пар будет конденсироваться с той же скоростью, что и жидкость. Таким образом, жидкость не может существовать постоянно, если испаряющаяся жидкость постоянно удаляется. ^[39] Жидкость, находящаяся при температуре кипения или выше, обычно закипает, хотя перегрев в определенных обстоятельствах может предотвратить это.

При температуре ниже точки замерзания жидкость имеет тенденцию кристаллизоваться , переходя в твердую форму. В отличие от перехода в газ, при этом переходе при постоянном давлении равновесия нет. ^{[ нужна ссылка ]} поэтому, если не произойдет переохлаждения , жидкость в конечном итоге полностью кристаллизуется. Однако это верно только при постоянном давлении, так что (например) вода и лед в закрытом прочном контейнере могут достичь равновесия, при котором обе фазы сосуществуют. О противоположном переходе из твердого состояния в жидкость см. плавление .

Жидкости в космосе

Фазовая диаграмма объясняет, почему жидкости не существуют в космосе или любом другом вакууме. Поскольку давление практически равно нулю (за исключением поверхностей или недр планет и лун), вода и другие жидкости, находящиеся в космосе, либо сразу же закипят, либо замерзнут в зависимости от температуры. В регионах космоса, близких к Земле, вода замерзает, если на нее не светит прямо солнце, и испаряется (возвышается), как только попадает на солнечный свет. Если вода существует на Луне в виде льда, то она может существовать только в затененных дырах, где никогда не светит солнце и где окружающие скалы не нагревают ее слишком сильно. В какой-то момент вблизи орбиты Сатурна свет Солнца слишком слаб, чтобы превратить лед в водяной пар. Об этом свидетельствует долговечность льда, составляющего кольца Сатурна. ^[40]

Решения

Жидкости могут образовывать растворы с газами, твердыми телами и другими жидкостями.

Две жидкости называются смешивающимися , если они могут образовывать раствор в любой пропорции; в противном случае они несмешиваемы. Например, вода и этанол (питьевой алкоголь) смешиваются, тогда как вода и бензин не смешиваются. ^[41] В некоторых случаях смесь несмешивающихся жидкостей можно стабилизировать с образованием эмульсии , в которой одна жидкость диспергируется в другой в виде микроскопических капель. требуется присутствие поверхностно-активного вещества Обычно для стабилизации капель . Известным примером эмульсии является майонез , который состоит из смеси воды и масла, стабилизированной лецитином , веществом, содержащимся в яичных желтках . ^[42]

Микроскопическое описание

Микроскопическая структура жидкостей сложна и исторически была предметом интенсивных исследований и дискуссий. ^[43]^[44]^[45]^[46] Некоторые из ключевых идей объяснены ниже.

Общее описание

Микроскопически жидкости представляют собой плотную неупорядоченную упаковку молекул. Это контрастирует с двумя другими распространенными фазами вещества: газами и твердыми телами. Хотя газы неупорядочены, молекулы хорошо разделены в пространстве и взаимодействуют преимущественно посредством столкновений между молекулами. И наоборот, хотя молекулы в твердых телах плотно упакованы, они обычно образуют правильную структуру, например кристаллическую решетку ( стекла являются заметнымисключение).

Ближний порядок

Хотя жидкости не обладают дальним упорядочением, как в кристаллической решетке, они обладают ближним порядком , который сохраняется на расстоянии нескольких диаметров молекул. ^[47]^[48]

Во всех жидкостях исключенные объемные взаимодействия вызывают ближний порядок в положениях молекул (координатах центра масс). Классические одноатомные жидкости, такие как аргон и криптон, являются простейшими примерами. Такие жидкости можно смоделировать как неупорядоченные «кучи» плотно упакованных сфер, а ближний порядок соответствует тому факту, что ближайшие и следующие ближайшие соседи в упаковке сфер имеют тенденцию быть разделенными целыми числами, кратными диаметру. ^[49]^[50]

В большинстве жидкостей молекулы не являются сферами, а межмолекулярные силы обладают направленностью, т. е. зависят от взаимной ориентации молекул. В результате в дополнение к упомянутому выше позиционному порядку существует ближний ориентационный порядок. Ориентационный порядок особенно важен в жидкостях с водородными связями, таких как вода. ^[51]^[52] Сила и направленный характер водородных связей способствуют образованию локальных «сетей» или «кластеров» молекул. Из-за относительной важности тепловых колебаний в жидкостях (по сравнению с твердыми телами) эти структуры очень динамичны, постоянно деформируются, разрушаются и реформируются. ^[49]^[51]

Энергия и энтропия

Микроскопические особенности жидкостей возникают в результате взаимодействия межмолекулярных сил притяжения и энтропийных сил . ^[53]

Силы притяжения имеют тенденцию притягивать молекулы близко друг к другу, и наряду с короткодействующими взаимодействиями отталкивания они являются доминирующими силами, лежащими в основе регулярной структуры твердых тел. Энтропийные силы не являются «силами» в механическом смысле; скорее, они описывают тенденцию системы максимизировать свою энтропию при фиксированной энергии (см. микроканонический ансамбль ). Грубо говоря, энтропийные силы отталкивают молекулы друг от друга, увеличивая занимаемый ими объем. Энтропийные силы преобладают в газах и объясняют тенденцию газов заполнять свои сосуды. В жидкостях, напротив, межмолекулярные и энтропийные силы сравнимы, поэтому пренебрегать одной в пользу другой нельзя. Количественно энергия связи между соседними молекулами того же порядка, что и тепловая энергия. $k_{\text{B}}T$ . ^[54]

Не малый параметр

Конкуренция между энергией и энтропией затрудняет моделирование жидкостей на молекулярном уровне, поскольку не существует идеализированного «эталонного состояния», которое могло бы служить отправной точкой для понятных теоретических описаний. Математически не существует малого параметра, на основе которого можно построить систематическую теорию возмущений . ^[44] Эта ситуация контрастирует как с газами, так и с твердыми телами. Для газов эталонным состоянием является идеальный газ , а плотность можно использовать как малый параметр для построения теории реальных (неидеальных) газов (см. вириальное разложение ). ^[55] Для кристаллических твердых тел эталонным состоянием является идеальная кристаллическая решетка, а возможными малыми параметрами являются тепловые движения и дефекты решетки . ^[51]

Роль квантовой механики

Как и все известные формы материи, жидкости по своей сути являются квантовомеханическими . Однако в стандартных условиях (около комнатной температуры и давления) большую часть макроскопического поведения жидкостей можно понять с точки зрения классической механики . ^[54]^[56] «Классическая картина» утверждает, что составляющие молекулы представляют собой дискретные объекты, которые взаимодействуют посредством межмолекулярных сил в соответствии с законами движения Ньютона . В результате их макроскопические свойства могут быть описаны с помощью классической статистической механики . Хотя закон межмолекулярных сил технически вытекает из квантовой механики, его обычно понимают как исходные данные модели для классической теории, полученные либо в результате соответствия экспериментальным данным, либо из классического предела квантовомеханического описания. ^[57]^[47] Наглядным, хотя и весьма упрощенным примером является совокупность сферических молекул, взаимодействующих посредством потенциала Леннарда-Джонса . ^[54]

Таблица 1: Тепловые длины волн де Бройля $\Lambda$ выбранных жидкостей. ^[54] Квантовые эффекты пренебрежимо малы, когда соотношение $\Lambda /a$ мал, где $a$ – среднее расстояние между молекулами.
Жидкость	Температура (К)	$\Lambda$ (нм)	$\Lambda /a$
Водород (H ₂ )	14.1	0.33	0.97
Неон	24.5	0.078	0.26
Криптон	116	0.018	0.046
Четыреххлористый углерод (CCl ₄ )	250	0.009	0.017

Для применения классического предела необходимым условием является то, что тепловая длина волны де Бройля ,

\Lambda =\left({\frac {2\pi \hbar ^{2}}{mk_{\text{B}}T}}\right)^{1/2}

мала по сравнению с рассматриваемым масштабом длины. ^[54]^[58] Здесь, $\hbar$ Планка постоянная и $m$ это масса молекулы. Типичные значения $\Lambda$ составляют около 0,01-0,1 нм (табл. 1). Следовательно, модель структуры жидкости с высоким разрешением на наноуровне может потребовать квантово-механических соображений. Ярким примером являются водородные связи в связанных жидкостях, таких как вода. ^[59]^[60] где из-за небольшой массы протона такие квантовые эффекты, как движение нулевой точки и туннелирование . важны ^[61]

Чтобы жидкость вела себя классически на макроскопическом уровне, $\Lambda$ должно быть небольшим по сравнению со средним расстоянием $a\approx \rho ^{-1/3}$ между молекулами. ^[54] То есть,

{\frac {\Lambda }{a}}\ll 1

Репрезентативные значения этого отношения для некоторых жидкостей приведены в таблице 1. Вывод состоит в том, что квантовые эффекты важны для жидкостей при низких температурах и с малой молекулярной массой . ^[54]^[56] Для динамических процессов существует дополнительное ограничение по времени:

\tau \gg {\frac {h}{k_{B}T}}

где $\tau$ – это временные рамки рассматриваемого процесса. Для жидкостей комнатной температуры правая часть составляет около 10 ⁻¹⁴ секунд, что обычно означает, что зависящие от времени процессы, включающие поступательное движение, могут быть описаны классически. ^[54]

При экстремально низких температурах даже макроскопическое поведение некоторых жидкостей отклоняется от классической механики. Яркими примерами являются водород и гелий. Благодаря низкой температуре и массе такие жидкости имеют тепловую длину волны де Бройля, сравнимую со средним расстоянием между молекулами. ^[54]

Динамические явления

Выражение для скорости звука жидкости:

c={\sqrt {K/\rho }}

,

содержит объемного сжатия K. модуль Если K не зависит от частоты, то жидкость ведет себя как линейная среда, так что звук распространяется без диссипации или связи мод . В действительности все жидкости демонстрируют некоторую дисперсию : с увеличением частоты K выходит за пределы низкочастотного жидкостного предела. $K_{0}$ до высокочастотного твердотельного предела $K_{\infty }$ . В нормальных жидкостях большая часть этого перехода происходит на частотах между ГГц и ТГц, иногда называемых гиперзвуком .

На частотах ниже ГГц нормальная жидкость не может выдерживать поперечные волны : предел нулевой частоты модуля сдвига равен 0. Иногда это рассматривают как определяющее свойство жидкости. ^[62]^[63] Однако, как и модуль объемного сжатия K , модуль сдвига G также зависит от частоты и демонстрирует аналогичный переход на гиперзвуковых частотах.

Согласно теории линейного отклика , преобразование Фурье K или G описывает, как система возвращается в равновесие после внешнего возмущения; по этой причине ступень дисперсии в диапазоне от ГГц до ТГц также называется релаксацией . По мере переохлаждения жидкости в сторону стеклования время структурной релаксации экспоненциально увеличивается, что объясняет вязкоупругое поведение стеклообразующих жидкостей.

Экспериментальные методы

Отсутствие дальнего порядка в жидкостях отражается отсутствием брэгговских пиков при рентгеновских лучей и дифракции нейтронов . В нормальных условиях дифракционная картина имеет круговую симметрию, выражающую изотропность жидкости. В радиальном направлении интенсивность дифракции плавно колеблется. Это можно описать статическим структурным фактором $S(q)$ , с волновым числом $q=(4\pi /\lambda )\sin \theta$ определяется длиной волны $\lambda$ зонда (фотона или нейтрона) и угла Брэгга $\theta$ . Колебания $S(q)$ выражают ближний порядок жидкости, т. е. корреляции между молекулой и «оболочками» ближайших соседей, следующих за ними соседей и т. д.

Эквивалентным представлением этих корреляций является функция радиального распределения $g(r)$ , что связано с Фурье преобразованием $S(q)$ . ^[49] Он представляет собой пространственное среднее временного снимка парных корреляций в жидкости.

Прогнозирование свойств жидкости

Методы прогнозирования свойств жидкости можно систематизировать по «шкале» описания, то есть по масштабам длины и времени, в которых они применяются. ^[64]^[65]

Макроскопические методы используют уравнения, которые напрямую моделируют крупномасштабное поведение жидкостей, например, их термодинамические свойства и поведение потока.
Микроскопические методы используют уравнения, моделирующие динамику отдельных молекул.
Мезоскопические методы занимают промежуточное положение, сочетая в себе элементы моделей континуума и моделей на основе частиц.

Макроскопический

Эмпирические корреляции

Эмпирические корреляции — это простые математические выражения, предназначенные для аппроксимации свойств жидкости в ряде экспериментальных условий, таких как изменение температуры и давления. ^[66] Они строятся путем подгонки простых функциональных форм к экспериментальным данным. Например, температурную зависимость вязкости жидкости иногда аппроксимируют функцией $\eta (T)=Ae^{B/T}$ , где $A$ и $B$ являются подгоночными константами. ^[67] Эмпирические корреляции позволяют чрезвычайно эффективно оценивать физические свойства, что может быть полезно при теплофизическом моделировании. Однако для хорошего соответствия им требуются высококачественные экспериментальные данные, и они не могут надежно экстраполироваться за пределы условий, охватываемых экспериментами.

Термодинамические потенциалы

Термодинамические потенциалы — это функции, характеризующие равновесное состояние вещества. Примером является свободная энергия Гиббса. $G(p,T)$ , который является функцией давления и температуры. Зная любой термодинамический потенциал ${\mathcal {F}}$ достаточно, чтобы вычислить все равновесные свойства вещества, часто просто взяв производные от ${\mathcal {F}}$ . ^[55] Таким образом, единая корреляция для ${\mathcal {F}}$ могут заменить отдельные корреляции для отдельных свойств. ^[68]^[69] И наоборот, в одну и ту же модель могут быть включены различные экспериментальные измерения (например, плотность, теплоемкость, давление пара); в принципе, это позволило бы прогнозировать трудноизмеримые свойства, такие как теплоемкость, с точки зрения других, более доступных измерений (например, давления пара). ^[70]

Гидродинамика

Гидродинамические теории описывают жидкости в терминах макроскопических полей , зависящих от пространства и времени , таких как плотность, скорость и температура. Эти поля подчиняются уравнениям в частных производных , которые могут быть линейными или нелинейными . ^[71] Гидродинамические теории являются более общими, чем равновесные термодинамические описания, которые предполагают, что жидкости примерно однородны и не зависят от времени. Уравнения Навье-Стокса являются хорошо известным примером: они представляют собой уравнения в частных производных, определяющие временную эволюцию плотности, скорости и температуры вязкой жидкости. Существует множество методов численного решения уравнений Навье-Стокса и их вариантов. ^[72]^[73]

мезоскопический

Мезоскопические методы работают на масштабах длины и времени между уровнями частиц и континуума. По этой причине они сочетают в себе элементы динамики частиц и гидродинамики сплошной среды. ^[64]

Примером может служить решеточный метод Больцмана , который моделирует жидкость как набор фиктивных частиц, существующих на решетке. ^[64] Частицы эволюционируют во времени посредством потокового (прямолинейного движения) и столкновений . Концептуально оно основано на уравнении Больцмана для разбавленных газов, где динамика молекулы состоит из свободного движения, прерываемого дискретными бинарными столкновениями, но оно также применяется и к жидкостям. Несмотря на аналогию с отдельными молекулярными траекториями, это грубое описание, которое обычно работает в масштабах длины и времени, больших, чем в истинной молекулярной динамике (отсюда и понятие «фиктивных» частиц).

Другие методы, сочетающие в себе элементы динамики континуума и динамики на уровне частиц, включают гидродинамику сглаженных частиц , ^[74]^[75] диссипативная динамика частиц , ^[76] и динамика многочастичных столкновений . ^[77]

микроскопический

Методы микроскопического моделирования работают непосредственно с уравнениями движения (классическими или квантовыми) составляющих молекул.

Классическая молекулярная динамика

Классическая молекулярная динамика (МД) моделирует жидкости, используя закон движения Ньютона; из второго закона Ньютона ( $F=m{\ddot {x}}$ ), траектории молекул можно явно проследить и использовать для расчета макроскопических свойств жидкости, таких как плотность или вязкость. Однако классическая МД требует выражений для межмолекулярных сил (« F » во втором законе Ньютона). Обычно их необходимо аппроксимировать с использованием экспериментальных данных или каких-либо других исходных данных. ^[47]

Ab initio (квантовая) молекулярная динамика

Квантово-механические методы ab initio моделируют жидкости, используя только законы квантовой механики и фундаментальные атомные константы. ^[57] В отличие от классической молекулярной динамики, межмолекулярные силовые поля являются результатом вычислений, а не входными данными, основанными на экспериментальных измерениях или других соображениях. В принципе, методы ab initio позволяют моделировать свойства данной жидкости без каких-либо предварительных экспериментальных данных. Однако они очень дороги в вычислительном отношении, особенно для больших молекул с внутренней структурой.

См. также

Ссылки

^ Теодор Грей, Элементы: визуальное исследование каждого известного атома во Вселенной Нью-Йорк: Workman Publishing, 2009, стр. 127 ISBN 1-57912-814-9
^ Леончук Сергей С.; Фальчевская Александра С.; Николаев, Виталий; Виноградов, Владимир Владимирович (2022). «Сплав NaK: недооцененный жидкий металл». Журнал химии материалов А. 10 (43). Королевское химическое общество (RSC): 22955–22976. дои : 10.1039/d2ta06882f . ISSN 2050-7488 . S2CID 252979251 .
^ Сурманн, Питер; Зеят, Ханан (15 октября 2005 г.). «Вольтамперометрический анализ с использованием самовозобновляемого безртутного электрода». Аналитическая и биоаналитическая химия . 383 (6). ООО «Спрингер Сайенс энд Бизнес Медиа»: 1009–1013. дои : 10.1007/s00216-005-0069-7 . ISSN 1618-2642 . ПМИД 16228199 . S2CID 22732411 .
^ Моттл, Майкл Дж.; Глейзер, Брайан Т.; Кайзер, Ральф И.; Мич, Карен Дж. (декабрь 2007 г.). «Вода и астробиология» (PDF) . Геохимия . 67 (4): 253–282. Бибкод : 2007ЧЭГ...67..253М . дои : 10.1016/j.chemer.2007.09.002 . ISSN 0009-2819 .
^ Чиба, Кристофер Ф.; Хэнд, Кевин П. (1 сентября 2005 г.). «Астробиология: исследование живой Вселенной». Ежегодный обзор астрономии и астрофизики . 43 (1): 31–74. Бибкод : 2005ARA&A..43...31C . doi : 10.1146/annurev.astro.43.051804.102202 . eISSN 1545-4282 . ISSN 0066-4146 .
^ Зильберберг, Мартин С. (2009), Химия: молекулярная природа материи и изменений , Высшее образование МакГроу-Хилла, стр. 448–449, ISBN 978-0-07-304859-8
^ Андриенко, Денис (октябрь 2018 г.). «Введение в жидкие кристаллы» . Журнал молекулярных жидкостей . 267 : 520–541. дои : 10.1016/j.molliq.2018.01.175 . ISSN 0167-7322 .
^ Тео Манг, Уилфрид Дрессел Смазочные материалы и смазка , Wiley-VCH 2007 ISBN 3-527-31497-0
^ Джордж Выпич Справочник растворителей William Andrew Publishing, 2001, стр. 847–881. ISBN 1-895198-24-0
^ Н. Б. Варгафтик Справочник по теплопроводности жидкостей и газов CRC Press 1994 г. ISBN 0-8493-9345-0
^ Джек Эрьявец Автомобильные технологии: системный подход Delmar Learning 2000 стр. 309 ISBN 1-4018-4831-1
^ Джеральд Вендт Перспективы ядерной энергетики и технологий Компания Д. Ван Ностранда, 1957 с. 266
^ Современная техника проектирования жидкостных ракетных двигателей Дитера К. Хузеля, Дэвида Х. Хуанга - Американский институт аэронавтики и астронавтики, 1992 г., с. 99 ISBN 1-56347-013-6
^ Томас Э. Малл, руководство по принципам и применению систем отопления, вентиляции и кондиционирования воздуха, McGraw-Hill, 1997 г. ISBN 0-07-044451-X
^ Эрл, РЛ (1983). Единичные операции в пищевой промышленности . Оксфорд: Пергамон Пресс. стр. 56–62, 138–141. ISBN 0-08-025537-Х . OCLC 8451210 .
^ Р. Кейт Мобли Гидродинамика Баттерворт-Хайнеманн, 2000 стр. VII ISBN 0-7506-7174-2
^ Дики, Майкл Д. (18 апреля 2017 г.). «Растягивающаяся и мягкая электроника с использованием жидких металлов» . Продвинутые материалы . 29 (27). Уайли: 1606425. Бибкод : 2017AdM....2906425D . дои : 10.1002/adma.201606425 . ISSN 0935-9648 . ПМИД 28417536 . S2CID 205276487 .
^ Коул, Тим; Хошманеш, Хашаяр; Тан, Ши-Ян (04 мая 2021 г.). «Биоустройства на основе жидкого металла». Передовые интеллектуальные системы . 3 (7). Вили: 2000275. doi : 10.1002/aisy.202000275 . ISSN 2640-4567 . S2CID 235568215 .
^ Тан, Ши-Ян; Табор, Кристофер; Калантар-Заде, Курош; Дики, Майкл Д. (26 июля 2021 г.). «Жидкий металл-галлий: эликсир дьявола» . Ежегодный обзор исследований материалов . 51 (1). Годовые обзоры: 381–408. Бибкод : 2021AnRMS..51..381T . doi : 10.1146/annurev-matsci-080819-125403 . ISSN 1531-7331 . S2CID 236566966 .
^ Бела Г. Липтак Справочник инженера по приборостроению: управление процессом CRC Press 1999 стр. 807 ISBN 0-8493-1081-4
^ Хиксон, Пол; Борра, Эрманно Ф.; Кабанак, Реми; Контент, Роберт; Гибсон, Брэд К.; Уокер, Гордон А.Х. (1994). «2,7-метровый телескоп с жидкостным зеркалом UBC / Лаваль». Астрофизический журнал . 436 . Американское астрономическое общество: L201. arXiv : astro-ph/9406057 . Бибкод : 1994ApJ...436L.201H . дои : 10.1086/187667 . ISSN 0004-637X .
^ Хиксон, Пол; Расин, Рене (2007). «Качество изображения жидкозеркальных телескопов» . Публикации Тихоокеанского астрономического общества . 119 (854). Издательство ИОП: 456–465. Бибкод : 2007PASP..119..456H . дои : 10.1086/517619 . ISSN 0004-6280 . S2CID 120735632 .
^ Найт, Рэндалл Д. (2008), Физика для ученых и инженеров: стратегический подход (с современной физикой) , Аддисон-Уэсли, с. 443 , ISBN 978-0-8053-2736-6
^ Зильберберг, Мартин С. (2009), Химия: молекулярная природа материи и изменений , Высшее образование МакГроу-Хилла, с. 461, ISBN 978-0-07-304859-8
^ «Сжимаемость жидкостей» . гиперфизика.phy-astr.gsu.edu . Архивировано из оригинала 7 декабря 2017 года . Проверено 8 мая 2018 г.
^ Интеллектуальное производство в энергетическом поле: междисциплинарные инновации в процессах , Вэньу Чжан - CRC Press 2011, стр. 144
^ Найт (2008) с. 454
^ Механика жидкости и гидравлические машины , SC Gupta - Дорлинг-Киндерсли, 2006 г., стр. 85
^ Найт (2008) с. 448
^ Найт (2008), стр. 455-459.
^ Зильберберг, Мартин С. (2009), Химия: молекулярная природа материи и изменений , Высшее образование McGraw-Hill, стр. 457, ISBN 978-0-07-304859-8
^ Edward Yu. Bormashenko (5 November 2018). Wetting of Real Surfaces . De Gruyter. pp. 3–5. ISBN 978-3-11-058314-4 .
^ Ландау, Л.Д.; Лифшиц, Э.М. (1987), Механика жидкости (2-е изд.), Pergamon Press, стр. 44–45, ISBN 978-0-08-033933-7
^ Берд, Р. Байрон; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (2007), Транспортные явления (2-е изд.), John Wiley & Sons, Inc., стр. 21, ISBN 978-0-470-11539-8
^ Жмудь, Борис (2014), «Уравнения смешивания вязкости» (PDF) , Lube-Tech , 93
^ «Индекс вязкости» . Великобритания: Антон Паар. Архивировано из оригинала 9 марта 2020 года . Проверено 29 августа 2018 г. .
^ Мед в традиционной и современной медицине , Лайд Букраа - CRC Press, 2014, стр. 22--24
^ Тейлор, Джон Р. (2005), Классическая механика , Университетские научные книги, стр. 727–729, ISBN 978-1-891389-22-1
^ Марш, Нью-Хэмпшир; Тоси, член парламента (2002), Введение в физику жидкого состояния , World Scientific, стр. 7, Бибкод : 2002ilsp.book.....M , doi : 10.1142/4717 , ISBN 978-981-3102-53-8
^ Сигел, Итан (11 декабря 2014 г.). «Вода в космосе замерзает или кипит?» . Начинается с треска! . Проверено 10 февраля 2022 г.
^ Зильберберг, стр. 188 и 502.
^ Миоданик, Марк (2019), «Жидкие правила: восхитительные и опасные вещества, которые протекают через нашу жизнь» , Houghton Mifflin Harcourt, стр. 124, ISBN 978-0-544-85019-4
^ Чендлер, Дэвид (5 мая 2017 г.). «50 лет назад зарождение современной науки о жидком состоянии». Ежегодный обзор физической химии . 68 (1). Годовые обзоры: 19–38. arXiv : 1609.04837 . Бибкод : 2017ARPC...68...19C . doi : 10.1146/annurev-physchem-052516-044941 . ISSN 0066-426X . ПМИД 28375691 . S2CID 37248336 .
^ Jump up to: Перейти обратно: ^а ^б Траченко, К; Бражкин, В.В. (22 декабря 2015 г.). «Коллективные режимы и термодинамика жидкого состояния». Отчеты о прогрессе в физике . 79 (1). Издание IOP: 016502. arXiv : 1512.06592 . дои : 10.1088/0034-4885/79/1/016502 . ISSN 0034-4885 . ПМИД 26696098 . S2CID 42203015 .
^ Бен-Наим, Арье (2009). Молекулярная теория воды и водных растворов. Часть 1. Понимание воды . Сингапур: World Scientific. ISBN 978-981-283-761-5 . OCLC 696342117 .
^ Поточки, Сильвия; Темлейтнер, Ласло; Пустаи, Ласло (01 декабря 2015 г.). «Структура чистых жидкостей, состоящих из (идеальных и почти) тетраэдрических молекул». Химические обзоры . 115 (24). Американское химическое общество (ACS): 13308–13361. doi : 10.1021/acs.chemrev.5b00308 . ISSN 0009-2665 . ПМИД 26624528 .
^ Jump up to: Перейти обратно: ^а ^б ^с Мейтленд, Джеффри К.; Ригби, Морис; Смит, Э. Брайан; Уэйкхэм, Вашингтон (1981). Межмолекулярные силы: их происхождение и определение . Оксфорд. ISBN 0-19-855611-Х . OCLC 8139179 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Галло, Паола; Ровере, Мауро (2021). Физика жидкого вещества . Чам: Спрингер. ISBN 978-3-030-68349-8 . OCLC 1259588062 .
^ Jump up to: Перейти обратно: ^а ^б ^с Чендлер, Дэвид (1987). Введение в современную статистическую механику . Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-504276-Х . OCLC 13946448 .
^ Финни, Джон Л. (22 февраля 2013 г.). «Путь Бернала к случайной упаковке и структуре жидкостей» . Философский журнал . 93 (31–33). Информа Великобритания Лимитед: 3940–3969. Бибкод : 2013PMag...93.3940F . дои : 10.1080/14786435.2013.770179 . ISSN 1478-6435 . S2CID 55689631 .
^ Jump up to: Перейти обратно: ^а ^б ^с Финни, JL (2015). Вода: очень краткое введение . Оксфорд, Великобритания. стр. 48–52. ISBN 978-0-19-870872-8 . OCLC 914537747 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Людвиг, Ральф (11 июля 2005 г.). «Строение жидкого метанола». ХимияФизХим . 6 (7). Уайли: 1369–1375 гг. дои : 10.1002/cphc.200400663 . ISSN 1439-4235 . ПМИД 15991270 .
^ Чендлер, Дэвид (8 сентября 2009 г.). «Жидкости: конденсированные, неупорядоченные и иногда сложные» . Труды Национальной академии наук . 106 (36): 15111–15112. дои : 10.1073/pnas.0908029106 . ISSN 0027-8424 . ПМЦ 2741213 . ПМИД 19805248 .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Хансен, Жан-Пьер; Макдональд, Ян Р. (2013). Теория простых жидкостей: с приложениями к мягким веществам . Амстердам. ISBN 978-0-12-387033-9 . OCLC 855895733 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Jump up to: Перейти обратно: ^а ^б Кардар, Мехран (2007). Статистическая физика частиц . Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. п. 130. ИСБН 978-0-521-87342-0 . OCLC 148639922 .
^ Jump up to: Перейти обратно: ^а ^б Грей, компьютерная графика; Габбинс, Кейт Э.; Джослин, CG (1984–2011). Теория молекулярных жидкостей . Оксфорд: Издательство Оксфордского университета. ISBN 0-19-855602-0 . OCLC 10145548 .
^ Jump up to: Перейти обратно: ^а ^б Маркс, Доминик; Хуттер, Юрг (2012). Молекулярная динамика ab initio: основная теория и передовые методы . Кембридж. ISBN 978-0-521-89863-8 . OCLC 869135580 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Фишер, И.З. (1964), Статистическая теория жидкостей , Издательство Чикагского университета.
^ Чериотти, Микеле; Кюни, Жером; Парринелло, Микеле; Манолопулос, Дэвид Э. (6 сентября 2013 г.). «Ядерные квантовые эффекты и флуктуации водородных связей в воде» . Труды Национальной академии наук . 110 (39): 15591–15596. Бибкод : 2013PNAS..11015591C . дои : 10.1073/pnas.1308560110 . ISSN 0027-8424 . ПМЦ 3785726 . ПМИД 24014589 .
^ Маркланд, Томас Э.; Чериотти, Микеле (28 февраля 2018 г.). «Ядерные квантовые эффекты становятся мейнстримом». Обзоры природы Химия . 2 (3). ООО «Спрингер Сайенс энд Бизнес Медиа». arXiv : 1803.01037 . дои : 10.1038/s41570-017-0109 . ISSN 2397-3358 . S2CID 4938804 .
^ Ли, Синь-Чжэн; Уокер, Брент; Михаэлидис, Ангелос (4 апреля 2011 г.). «Квантовая природа водородной связи» . Труды Национальной академии наук . 108 (16): 6369–6373. Бибкод : 2011PNAS..108.6369L . дои : 10.1073/pnas.1016653108 . ISSN 0027-8424 . ПМК 3081025 .
^ Родился Макс (1940). «Об устойчивости кристаллических решеток». Математические труды . 36 (2). Кембриджское философское общество: 160–172. Бибкод : 1940PCPS...36..160B . дои : 10.1017/S0305004100017138 . S2CID 104272002 .
^ Родился Макс (1939). «Термодинамика кристаллов и плавление» . Журнал химической физики . 7 (8): 591–604. Бибкод : 1939ЖЧФ...7..591Б . дои : 10.1063/1.1750497 . Архивировано из оригинала 15 мая 2016 г.
^ Jump up to: Перейти обратно: ^а ^б ^с Крюгер, Тимм; Кусумаатмаджа, Халим; Кузьмин Александр; Шардт, Орест; Силва, Гонсало; Вигген, Эрленд Магнус (2016). Решетчатый метод Больцмана: принципы и практика . Швейцария. ISBN 978-3-319-44649-3 . OCLC 963198053 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Штайнхаузер, Миссури (2022 г.). Вычислительное многомасштабное моделирование жидкостей и твердых тел: теория и приложения . Чам, Швейцария: Springer. ISBN 978-3-030-98954-5 . OCLC 1337924123 .
^ Полинг, Брюс Э.; Праусниц, Дж. М.; О'Коннелл, Джон П. (2001). Свойства газов и жидкостей . Нью-Йорк: МакГроу-Хилл. ISBN 0-07-011682-2 . OCLC 44712950 .
^ Берд, Р. Байрон; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (2007). Транспортные явления (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-470-11539-8 . Архивировано из оригинала 2 марта 2020 г. Проверено 18 сентября 2019 г.
^ Спан, Р. (2000). Многопараметрические уравнения состояния: точный источник данных о термодинамических свойствах . Инженерная онлайн-библиотека. Спрингер. п. 1. ISBN 978-3-540-67311-8 . Проверено 1 апреля 2023 г.
^ Хубер, Марсия Л.; Леммон, Эрик В.; Белл, Ян Х.; Маклинден, Марк О. (22 июня 2022 г.). «База данных NIST REFPROP для высокоточных свойств промышленно важных жидкостей» . Исследования в области промышленной и инженерной химии . 61 (42). Американское химическое общество (ACS): 15449–15472. doi : 10.1021/acs.iecr.2c01427 . ISSN 0888-5885 . ПМК 9619405 . ПМИД 36329835 . S2CID 249968848 .
^ Тилнер-Рот, Райнер; Друг, Дэниел Г. (1998). «Формулировка термодинамических свойств смеси {вода + аммиак} на основе свободной энергии Гельмгольца». Журнал физических и химических справочных данных . 27 (1). Издательство АИП: 63–96. дои : 10.1063/1.556015 . ISSN 0047-2689 .
^ Моффатт, Гонконг (2015), «Гидродинамика», Николас Дж. Хайэм; и др. (ред.), Princeton Companion to Applied Mathematics , Princeton University Press, стр. 467–476.
^ Вендт, Джон Ф.; Андерсон, Джон Д. младший; Институт гидродинамики фон Кармана (2008). Вычислительная гидродинамика: введение . Берлин: Шпрингер. ISBN 978-3-540-85056-4 . OCLC 656397653 .
^ Позрикидис, К. (2011). Введение в теоретическую и вычислительную гидродинамику . Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-990912-4 . OCLC 812917029 .
^ Монаган, Джей-Джей (5 июля 2005 г.). «Гидродинамика сглаженных частиц». Отчеты о прогрессе в физике . 68 (8). Издательство ИОП: 1703–1759. Бибкод : 2005РПФ...68.1703М . дои : 10.1088/0034-4885/68/8/r01 . ISSN 0034-4885 . S2CID 5987481 .
^ Линд, Стивен Дж.; Роджерс, Бенедикт Д.; Стэнсби, Питер К. (2020). «Обзор гидродинамики сглаженных частиц: к моделированию сходящихся лагранжевых потоков» . Труды Королевского общества A: Математические, физические и технические науки . 476 (2241). Королевское общество. Бибкод : 2020RSPSA.47690801L . дои : 10.1098/rspa.2019.0801 . ISSN 1364-5021 . ПМЦ 7544338 . ПМИД 33071565 . S2CID 221538477 .
^ Эспаньол, Пеп; Уоррен, Патрик Б. (21 апреля 2017 г.). «Перспектива: динамика диссипативных частиц». Журнал химической физики . 146 (15). Издательство AIP: 150901. arXiv : 1612.04574 . Бибкод : 2017JChPh.146o0901E . дои : 10.1063/1.4979514 . ISSN 0021-9606 . ПМИД 28433024 . S2CID 961922 .
^ Гомппер, Г.; Илье, Т.; Кролл, Д.М.; Винклер, Р.Г. (2009). «Динамика многочастичных столкновений: мезомасштабный подход к гидродинамике сложных жидкостей на основе частиц». Передовые подходы к компьютерному моделированию наук о мягких веществах III . Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 1–87. arXiv : 0808.2157 . дои : 10.1007/978-3-540-87706-6_1 . ISBN 978-3-540-87705-9 . S2CID 8433369 .

[1] Теодор Грей, Элементы: визуальное исследование каждого известного атома во Вселенной Нью-Йорк: Workman Publishing, 2009, стр. 127 ISBN 1-57912-814-9

[Leonchuk2022-2] Леончук Сергей С.; Фальчевская Александра С.; Николаев, Виталий; Виноградов, Владимир Владимирович (2022). «Сплав NaK: недооцененный жидкий металл». Журнал химии материалов А. 10 (43). Королевское химическое общество (RSC): 22955–22976. дои : 10.1039/d2ta06882f . ISSN 2050-7488 . S2CID 252979251 .

[Surmann2005-3] Сурманн, Питер; Зеят, Ханан (15 октября 2005 г.). «Вольтамперометрический анализ с использованием самовозобновляемого безртутного электрода». Аналитическая и биоаналитическая химия . 383 (6). ООО «Спрингер Сайенс энд Бизнес Медиа»: 1009–1013. дои : 10.1007/s00216-005-0069-7 . ISSN 1618-2642 . ПМИД 16228199 . S2CID 22732411 .

[MottlGlazerKaiser2007-4] Моттл, Майкл Дж.; Глейзер, Брайан Т.; Кайзер, Ральф И.; Мич, Карен Дж. (декабрь 2007 г.). «Вода и астробиология» (PDF) . Геохимия . 67 (4): 253–282. Бибкод : 2007ЧЭГ...67..253М . дои : 10.1016/j.chemer.2007.09.002 . ISSN 0009-2819 .

[ChybaHand2005-5] Чиба, Кристофер Ф.; Хэнд, Кевин П. (1 сентября 2005 г.). «Астробиология: исследование живой Вселенной». Ежегодный обзор астрономии и астрофизики . 43 (1): 31–74. Бибкод : 2005ARA&A..43...31C . doi : 10.1146/annurev.astro.43.051804.102202 . eISSN 1545-4282 . ISSN 0066-4146 .

[6] Зильберберг, Мартин С. (2009), Химия: молекулярная природа материи и изменений , Высшее образование МакГроу-Хилла, стр. 448–449, ISBN 978-0-07-304859-8

[Andrienko2018-7] Андриенко, Денис (октябрь 2018 г.). «Введение в жидкие кристаллы» . Журнал молекулярных жидкостей . 267 : 520–541. дои : 10.1016/j.molliq.2018.01.175 . ISSN 0167-7322 .

[8] Тео Манг, Уилфрид Дрессел Смазочные материалы и смазка , Wiley-VCH 2007 ISBN 3-527-31497-0

[9] Джордж Выпич Справочник растворителей William Andrew Publishing, 2001, стр. 847–881. ISBN 1-895198-24-0

[10] Н. Б. Варгафтик Справочник по теплопроводности жидкостей и газов CRC Press 1994 г. ISBN 0-8493-9345-0

[11] Джек Эрьявец Автомобильные технологии: системный подход Delmar Learning 2000 стр. 309 ISBN 1-4018-4831-1

[12] Джеральд Вендт Перспективы ядерной энергетики и технологий Компания Д. Ван Ностранда, 1957 с. 266

[13] Современная техника проектирования жидкостных ракетных двигателей Дитера К. Хузеля, Дэвида Х. Хуанга - Американский институт аэронавтики и астронавтики, 1992 г., с. 99 ISBN 1-56347-013-6

[14] Томас Э. Малл, руководство по принципам и применению систем отопления, вентиляции и кондиционирования воздуха, McGraw-Hill, 1997 г. ISBN 0-07-044451-X

[Earle1983-15] Эрл, РЛ (1983). Единичные операции в пищевой промышленности . Оксфорд: Пергамон Пресс. стр. 56–62, 138–141. ISBN 0-08-025537-Х . OCLC 8451210 .

[16] Р. Кейт Мобли Гидродинамика Баттерворт-Хайнеманн, 2000 стр. VII ISBN 0-7506-7174-2

[Dickey2017-17] Дики, Майкл Д. (18 апреля 2017 г.). «Растягивающаяся и мягкая электроника с использованием жидких металлов» . Продвинутые материалы . 29 (27). Уайли: 1606425. Бибкод : 2017AdM....2906425D . дои : 10.1002/adma.201606425 . ISSN 0935-9648 . ПМИД 28417536 . S2CID 205276487 .

[ColeKhoshmaneshTang2021-18] Коул, Тим; Хошманеш, Хашаяр; Тан, Ши-Ян (04 мая 2021 г.). «Биоустройства на основе жидкого металла». Передовые интеллектуальные системы . 3 (7). Вили: 2000275. doi : 10.1002/aisy.202000275 . ISSN 2640-4567 . S2CID 235568215 .

[TangTaborKalantar-ZadehDickey2021-19] Тан, Ши-Ян; Табор, Кристофер; Калантар-Заде, Курош; Дики, Майкл Д. (26 июля 2021 г.). «Жидкий металл-галлий: эликсир дьявола» . Ежегодный обзор исследований материалов . 51 (1). Годовые обзоры: 381–408. Бибкод : 2021AnRMS..51..381T . doi : 10.1146/annurev-matsci-080819-125403 . ISSN 1531-7331 . S2CID 236566966 .

[20] Бела Г. Липтак Справочник инженера по приборостроению: управление процессом CRC Press 1999 стр. 807 ISBN 0-8493-1081-4

[Hickson1994-21] Хиксон, Пол; Борра, Эрманно Ф.; Кабанак, Реми; Контент, Роберт; Гибсон, Брэд К.; Уокер, Гордон А.Х. (1994). «2,7-метровый телескоп с жидкостным зеркалом UBC / Лаваль». Астрофизический журнал . 436 . Американское астрономическое общество: L201. arXiv : astro-ph/9406057 . Бибкод : 1994ApJ...436L.201H . дои : 10.1086/187667 . ISSN 0004-637X .

[Hickson2007-22] Хиксон, Пол; Расин, Рене (2007). «Качество изображения жидкозеркальных телескопов» . Публикации Тихоокеанского астрономического общества . 119 (854). Издательство ИОП: 456–465. Бибкод : 2007PASP..119..456H . дои : 10.1086/517619 . ISSN 0004-6280 . S2CID 120735632 .

[23] Найт, Рэндалл Д. (2008), Физика для ученых и инженеров: стратегический подход (с современной физикой) , Аддисон-Уэсли, с. 443 , ISBN 978-0-8053-2736-6

[24] Зильберберг, Мартин С. (2009), Химия: молекулярная природа материи и изменений , Высшее образование МакГроу-Хилла, с. 461, ISBN 978-0-07-304859-8

[25] «Сжимаемость жидкостей» . гиперфизика.phy-astr.gsu.edu . Архивировано из оригинала 7 декабря 2017 года . Проверено 8 мая 2018 г.

[ReferenceA-26] Интеллектуальное производство в энергетическом поле: междисциплинарные инновации в процессах , Вэньу Чжан - CRC Press 2011, стр. 144

[27] Найт (2008) с. 454

[28] Механика жидкости и гидравлические машины , SC Gupta - Дорлинг-Киндерсли, 2006 г., стр. 85

[29] Найт (2008) с. 448

[30] Найт (2008), стр. 455-459.

[31] Зильберберг, Мартин С. (2009), Химия: молекулярная природа материи и изменений , Высшее образование McGraw-Hill, стр. 457, ISBN 978-0-07-304859-8

[Bormashenko2018-32] Edward Yu. Bormashenko (5 November 2018). Wetting of Real Surfaces . De Gruyter. pp. 3–5. ISBN 978-3-11-058314-4 .

[33] Ландау, Л.Д.; Лифшиц, Э.М. (1987), Механика жидкости (2-е изд.), Pergamon Press, стр. 44–45, ISBN 978-0-08-033933-7

[34] Берд, Р. Байрон; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (2007), Транспортные явления (2-е изд.), John Wiley & Sons, Inc., стр. 21, ISBN 978-0-470-11539-8

[Zhmud2014-35] Жмудь, Борис (2014), «Уравнения смешивания вязкости» (PDF) , Lube-Tech , 93

[36] «Индекс вязкости» . Великобритания: Антон Паар. Архивировано из оригинала 9 марта 2020 года . Проверено 29 августа 2018 г. .

[37] Мед в традиционной и современной медицине , Лайд Букраа - CRC Press, 2014, стр. 22--24

[38] Тейлор, Джон Р. (2005), Классическая механика , Университетские научные книги, стр. 727–729, ISBN 978-1-891389-22-1

[39] Марш, Нью-Хэмпшир; Тоси, член парламента (2002), Введение в физику жидкого состояния , World Scientific, стр. 7, Бибкод : 2002ilsp.book.....M , doi : 10.1142/4717 , ISBN 978-981-3102-53-8

[40] Сигел, Итан (11 декабря 2014 г.). «Вода в космосе замерзает или кипит?» . Начинается с треска! . Проверено 10 февраля 2022 г.

[41] Зильберберг, стр. 188 и 502.

[42] Миоданик, Марк (2019), «Жидкие правила: восхитительные и опасные вещества, которые протекают через нашу жизнь» , Houghton Mifflin Harcourt, стр. 124, ISBN 978-0-544-85019-4

[Chandler2017-43] Чендлер, Дэвид (5 мая 2017 г.). «50 лет назад зарождение современной науки о жидком состоянии». Ежегодный обзор физической химии . 68 (1). Годовые обзоры: 19–38. arXiv : 1609.04837 . Бибкод : 2017ARPC...68...19C . doi : 10.1146/annurev-physchem-052516-044941 . ISSN 0066-426X . ПМИД 28375691 . S2CID 37248336 .

[TrachenkoBrazhkin2015-44] Jump up to: Перейти обратно: ^а ^б Траченко, К; Бражкин, В.В. (22 декабря 2015 г.). «Коллективные режимы и термодинамика жидкого состояния». Отчеты о прогрессе в физике . 79 (1). Издание IOP: 016502. arXiv : 1512.06592 . дои : 10.1088/0034-4885/79/1/016502 . ISSN 0034-4885 . ПМИД 26696098 . S2CID 42203015 .

[Ben-Naim2009-45] Бен-Наим, Арье (2009). Молекулярная теория воды и водных растворов. Часть 1. Понимание воды . Сингапур: World Scientific. ISBN 978-981-283-761-5 . OCLC 696342117 .

[Pothoczki2015-46] Поточки, Сильвия; Темлейтнер, Ласло; Пустаи, Ласло (01 декабря 2015 г.). «Структура чистых жидкостей, состоящих из (идеальных и почти) тетраэдрических молекул». Химические обзоры . 115 (24). Американское химическое общество (ACS): 13308–13361. doi : 10.1021/acs.chemrev.5b00308 . ISSN 0009-2665 . ПМИД 26624528 .

[Maitland1981-47] Jump up to: Перейти обратно: ^а ^б ^с Мейтленд, Джеффри К.; Ригби, Морис; Смит, Э. Брайан; Уэйкхэм, Вашингтон (1981). Межмолекулярные силы: их происхождение и определение . Оксфорд. ISBN 0-19-855611-Х . OCLC 8139179 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[GalloRovere2021-48] Галло, Паола; Ровере, Мауро (2021). Физика жидкого вещества . Чам: Спрингер. ISBN 978-3-030-68349-8 . OCLC 1259588062 .

[Chandler1987-49] Jump up to: Перейти обратно: ^а ^б ^с Чендлер, Дэвид (1987). Введение в современную статистическую механику . Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-504276-Х . OCLC 13946448 .

[Finney2013-50] Финни, Джон Л. (22 февраля 2013 г.). «Путь Бернала к случайной упаковке и структуре жидкостей» . Философский журнал . 93 (31–33). Информа Великобритания Лимитед: 3940–3969. Бибкод : 2013PMag...93.3940F . дои : 10.1080/14786435.2013.770179 . ISSN 1478-6435 . S2CID 55689631 .

[Finney2015-51] Jump up to: Перейти обратно: ^а ^б ^с Финни, JL (2015). Вода: очень краткое введение . Оксфорд, Великобритания. стр. 48–52. ISBN 978-0-19-870872-8 . OCLC 914537747 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[Ludwig2005-52] Людвиг, Ральф (11 июля 2005 г.). «Строение жидкого метанола». ХимияФизХим . 6 (7). Уайли: 1369–1375 гг. дои : 10.1002/cphc.200400663 . ISSN 1439-4235 . ПМИД 15991270 .

[Chandler2009-53] Чендлер, Дэвид (8 сентября 2009 г.). «Жидкости: конденсированные, неупорядоченные и иногда сложные» . Труды Национальной академии наук . 106 (36): 15111–15112. дои : 10.1073/pnas.0908029106 . ISSN 0027-8424 . ПМЦ 2741213 . ПМИД 19805248 .

[HansenMcDonald2013-54] Jump up to: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Хансен, Жан-Пьер; Макдональд, Ян Р. (2013). Теория простых жидкостей: с приложениями к мягким веществам . Амстердам. ISBN 978-0-12-387033-9 . OCLC 855895733 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[Kardar_2007_p.-55] Jump up to: Перейти обратно: ^а ^б Кардар, Мехран (2007). Статистическая физика частиц . Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. п. 130. ИСБН 978-0-521-87342-0 . OCLC 148639922 .

[Gray1984-56] Jump up to: Перейти обратно: ^а ^б Грей, компьютерная графика; Габбинс, Кейт Э.; Джослин, CG (1984–2011). Теория молекулярных жидкостей . Оксфорд: Издательство Оксфордского университета. ISBN 0-19-855602-0 . OCLC 10145548 .

[MarxHutter_2012-57] Jump up to: Перейти обратно: ^а ^б Маркс, Доминик; Хуттер, Юрг (2012). Молекулярная динамика ab initio: основная теория и передовые методы . Кембридж. ISBN 978-0-521-89863-8 . OCLC 869135580 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[58] Фишер, И.З. (1964), Статистическая теория жидкостей , Издательство Чикагского университета.

[Ceriotti2013-59] Чериотти, Микеле; Кюни, Жером; Парринелло, Микеле; Манолопулос, Дэвид Э. (6 сентября 2013 г.). «Ядерные квантовые эффекты и флуктуации водородных связей в воде» . Труды Национальной академии наук . 110 (39): 15591–15596. Бибкод : 2013PNAS..11015591C . дои : 10.1073/pnas.1308560110 . ISSN 0027-8424 . ПМЦ 3785726 . ПМИД 24014589 .

[Markland_Ceriotti2018-60] Маркланд, Томас Э.; Чериотти, Микеле (28 февраля 2018 г.). «Ядерные квантовые эффекты становятся мейнстримом». Обзоры природы Химия . 2 (3). ООО «Спрингер Сайенс энд Бизнес Медиа». arXiv : 1803.01037 . дои : 10.1038/s41570-017-0109 . ISSN 2397-3358 . S2CID 4938804 .

[Li2011-61] Ли, Синь-Чжэн; Уокер, Брент; Михаэлидис, Ангелос (4 апреля 2011 г.). «Квантовая природа водородной связи» . Труды Национальной академии наук . 108 (16): 6369–6373. Бибкод : 2011PNAS..108.6369L . дои : 10.1073/pnas.1016653108 . ISSN 0027-8424 . ПМК 3081025 .

[62] Родился Макс (1940). «Об устойчивости кристаллических решеток». Математические труды . 36 (2). Кембриджское философское общество: 160–172. Бибкод : 1940PCPS...36..160B . дои : 10.1017/S0305004100017138 . S2CID 104272002 .

[63] Родился Макс (1939). «Термодинамика кристаллов и плавление» . Журнал химической физики . 7 (8): 591–604. Бибкод : 1939ЖЧФ...7..591Б . дои : 10.1063/1.1750497 . Архивировано из оригинала 15 мая 2016 г.

[Krüger2016-64] Jump up to: Перейти обратно: ^а ^б ^с Крюгер, Тимм; Кусумаатмаджа, Халим; Кузьмин Александр; Шардт, Орест; Силва, Гонсало; Вигген, Эрленд Магнус (2016). Решетчатый метод Больцмана: принципы и практика . Швейцария. ISBN 978-3-319-44649-3 . OCLC 963198053 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[Steinhauser2022-65] Штайнхаузер, Миссури (2022 г.). Вычислительное многомасштабное моделирование жидкостей и твердых тел: теория и приложения . Чам, Швейцария: Springer. ISBN 978-3-030-98954-5 . OCLC 1337924123 .

[Poling2001-66] Полинг, Брюс Э.; Праусниц, Дж. М.; О'Коннелл, Джон П. (2001). Свойства газов и жидкостей . Нью-Йорк: МакГроу-Хилл. ISBN 0-07-011682-2 . OCLC 44712950 .

[67] Берд, Р. Байрон; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (2007). Транспортные явления (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-470-11539-8 . Архивировано из оригинала 2 марта 2020 г. Проверено 18 сентября 2019 г.

[Span2000-68] Спан, Р. (2000). Многопараметрические уравнения состояния: точный источник данных о термодинамических свойствах . Инженерная онлайн-библиотека. Спрингер. п. 1. ISBN 978-3-540-67311-8 . Проверено 1 апреля 2023 г.

[Huber2022-69] Хубер, Марсия Л.; Леммон, Эрик В.; Белл, Ян Х.; Маклинден, Марк О. (22 июня 2022 г.). «База данных NIST REFPROP для высокоточных свойств промышленно важных жидкостей» . Исследования в области промышленной и инженерной химии . 61 (42). Американское химическое общество (ACS): 15449–15472. doi : 10.1021/acs.iecr.2c01427 . ISSN 0888-5885 . ПМК 9619405 . ПМИД 36329835 . S2CID 249968848 .

[Tillner-Roth1998-70] Тилнер-Рот, Райнер; Друг, Дэниел Г. (1998). «Формулировка термодинамических свойств смеси {вода + аммиак} на основе свободной энергии Гельмгольца». Журнал физических и химических справочных данных . 27 (1). Издательство АИП: 63–96. дои : 10.1063/1.556015 . ISSN 0047-2689 .

[PrincetonCompanion-71] Моффатт, Гонконг (2015), «Гидродинамика», Николас Дж. Хайэм; и др. (ред.), Princeton Companion to Applied Mathematics , Princeton University Press, стр. 467–476.

[Wendt2008-72] Вендт, Джон Ф.; Андерсон, Джон Д. младший; Институт гидродинамики фон Кармана (2008). Вычислительная гидродинамика: введение . Берлин: Шпрингер. ISBN 978-3-540-85056-4 . OCLC 656397653 .

[Pozrikidis2011-73] Позрикидис, К. (2011). Введение в теоретическую и вычислительную гидродинамику . Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-990912-4 . OCLC 812917029 .

[Monaghan2005-74] Монаган, Джей-Джей (5 июля 2005 г.). «Гидродинамика сглаженных частиц». Отчеты о прогрессе в физике . 68 (8). Издательство ИОП: 1703–1759. Бибкод : 2005РПФ...68.1703М . дои : 10.1088/0034-4885/68/8/r01 . ISSN 0034-4885 . S2CID 5987481 .

[Lind2020-75] Линд, Стивен Дж.; Роджерс, Бенедикт Д.; Стэнсби, Питер К. (2020). «Обзор гидродинамики сглаженных частиц: к моделированию сходящихся лагранжевых потоков» . Труды Королевского общества A: Математические, физические и технические науки . 476 (2241). Королевское общество. Бибкод : 2020RSPSA.47690801L . дои : 10.1098/rspa.2019.0801 . ISSN 1364-5021 . ПМЦ 7544338 . ПМИД 33071565 . S2CID 221538477 .

[Español2017-76] Эспаньол, Пеп; Уоррен, Патрик Б. (21 апреля 2017 г.). «Перспектива: динамика диссипативных частиц». Журнал химической физики . 146 (15). Издательство AIP: 150901. arXiv : 1612.04574 . Бибкод : 2017JChPh.146o0901E . дои : 10.1063/1.4979514 . ISSN 0021-9606 . ПМИД 28433024 . S2CID 961922 .

[Gompper2008-77] Гомппер, Г.; Илье, Т.; Кролл, Д.М.; Винклер, Р.Г. (2009). «Динамика многочастичных столкновений: мезомасштабный подход к гидродинамике сложных жидкостей на основе частиц». Передовые подходы к компьютерному моделированию наук о мягких веществах III . Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 1–87. arXiv : 0808.2157 . дои : 10.1007/978-3-540-87706-6_1 . ISBN 978-3-540-87705-9 . S2CID 8433369 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

v т и Состояния материи ( список )
State	Solid Liquid Gas / Vapor Supercritical fluid Plasma
Low energy	Bose–Einstein condensate Fermionic condensate Degenerate matter Quantum Hall Rydberg matter Strange matter Superfluid Supersolid Photonic molecule
High energy	QCD matter Quark–gluon plasma Color-glass condensate
Other states	Colloid Crystal Liquid crystal Time crystal Quantum spin liquid Exotic matter Programmable matter Dark matter Antimatter Magnetically ordered Antiferromagnet Ferrimagnet Ferromagnet String-net liquid Superglass
Transitions	Boiling Boiling point Condensation Critical line Critical point Crystallization Deposition Evaporation Flash evaporation Freezing Chemical ionization Ionization Lambda point Melting Melting point Recombination Regelation Saturated fluid Sublimation Supercooling Triple point Vaporization Vitrification
Quantities	Enthalpy of fusion Enthalpy of sublimation Enthalpy of vaporization Latent heat Latent internal energy Trouton's rule Volatility
Concepts	Baryonic matter Binodal Compressed fluid Cooling curve Equation of state Leidenfrost effect Macroscopic quantum phenomena Mpemba effect Order and disorder (physics) Spinodal Superconductivity Superheated vapor Superheating Thermo-dielectric effect