Вириальное расширение

Вириальное расширение представляет собой модель термодинамических уравнений состояния . Он выражает давление $P$ газа в локальном равновесии как ряд плотности степенной . представить через коэффициент сжимаемости Z $как$ Это уравнение можно $Z\equiv {\frac {P}{RT\rho }}=A+B\rho +C\rho ^{2}+\cdots$ Это уравнение было впервые предложено Камерлингом-Оннесом . ^[1] Члены $A$ , $B$ и $C$ представляют вириальные коэффициенты . Старший коэффициент $A$ определяется как постоянное значение 1, что гарантирует, что уравнение сводится к выражению идеального газа , когда плотность газа приближается к нулю.

Второй и третий вириальные коэффициенты

Второй, $B$ , и третий, $C$ , вириальные коэффициенты широко изучались и сводились в таблицы для многих жидкостей уже более столетия. Два самых обширных сборника находятся в книгах Даймонда. ^[2]^[3] и Национального института стандартов и технологий. база данных Thermo Data Engine ^[4] и его веб-термотаблицы. ^[5] В эти сборники включены таблицы вторых и третьих вириальных коэффициентов многих жидкостей.

Приведение уравнений состояния к вириальной форме

Большинство уравнений состояния можно переформулировать и преобразовать в вириальные уравнения, чтобы оценить и сравнить их неявные второй и третий вириальные коэффициенты. Основополагающее Ван дер Ваальса уравнение состояния ^[6] было предложено в 1873 году: $P={\frac {RT}{\left(v-b\right)}}-{\frac {a}{v^{2}}}$ где $v = 1/ ρ$ — мольный объем. Его можно переставить, разложив $1/(v - b)$ в ряд Тейлора : $Z=1+\left(b-{\frac {a}{RT}}\right)\rho +b^{2}\rho ^{2}+b^{3}\rho ^{3}+\cdots$

В уравнении Ван-дер-Ваальса второй вириальный коэффициент ведет себя примерно правильно, поскольку он монотонно убывает при понижении температуры. Третий и более высокие вириальные коэффициенты не зависят от температуры и неверны, особенно при низких температурах.

Почти все последующие уравнения состояния выводятся из уравнения Ван-дер-Ваальса, как и уравнения Дитеричи: ^[7] Бертло, ^[8] Редлих Квонг, ^[9] и Пэн-Робинсон ^[10] страдают от особенности, вносимой $1/(v - b)$ .

Другие уравнения состояния, начатые Битти и Бриджменом, ^[11] более тесно связаны с вириальными уравнениями и более точно отражают поведение жидкостей как в газообразной, так и в жидкой фазах. ^{[ нужна ссылка ]} Уравнение состояния Битти-Бриджмена, предложенное в 1928 году: $p={\frac {RT}{v^{2}}}\left(1-{\frac {c}{vT^{3}}}\right)(v+B)-{\frac {A}{v^{2}}}$ где

$A=A_{0}\left(1-{\frac {a}{v}}\right)$
$B=B_{0}\left(1-{\frac {b}{v}}\right)$

можно переставить как $Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {c}{T^{3}}}\right)\rho -\left(B_{0}b-{\frac {A_{0}a}{RT}}+{\frac {B_{0}c}{T^{3}}}\right)\rho ^{2}+\left({\frac {B_{0}bc}{T^{3}}}\right)\rho ^{3}$ Уравнение состояния Бенедикта-Уэбба-Рубина ^[12] 1940 года представляет собой лучшие изотермы ниже критической температуры: $Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {C_{0}}{RT^{3}}}\right)\rho +\left(b-{\frac {a}{RT}}\right)\rho ^{2}+\left({\frac {\alpha a}{RT}}\right)\rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\gamma \rho ^{2}\right)$

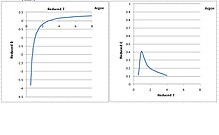
Больше улучшений было достигнуто Старлингом ^[13] в 1972 году: $Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {C_{0}}{RT^{3}}}+{\frac {D_{0}}{RT^{4}}}-{\frac {E_{0}}{RT^{5}}}\right)\rho +\left(b-{\frac {a}{RT}}-{\frac {d}{RT^{2}}}\right)\rho ^{2}+\alpha \left({\frac {a}{RT}}+{\frac {d}{RT^{2}}}\right)\rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\gamma \rho ^{2}\right)$

Ниже приведены графики приведенных второго и третьего вириальных коэффициентов в зависимости от пониженной температуры по Старлингу: ^[13]

Экспоненциальные члены в последних двух уравнениях корректируют третий вириальный коэффициент, так что изотермы в жидкой фазе могут быть представлены правильно. Экспоненциальный член быстро сходится по мере увеличения ρ, и если взять только первые два члена в его ряду Тейлора, $1-\gamma \rho ^{2}$ , и умноженный на $1+\gamma \rho ^{2}$ , результат $1-\gamma ^{2}\rho ^{4}$ , что способствует $c/RT^{3}$ член к третьему вириальному коэффициенту и один член к восьмому вириальному коэффициенту, которым можно пренебречь. ^{[ оригинальное исследование? ]}

После разложения экспоненциальных членов уравнения состояния Бенедикта-Уэбба-Рубина и Старлинга имеют следующий вид: $Z=1+b\rho _{r}+c\rho _{r}^{2}+f\rho _{r}^{5}$

Кубическое вириальное уравнение состояния

Трехчленное вириальное уравнение или кубическое вириальное уравнение состояния $Z=1+B\rho +C\rho ^{2}$ имеет простоту уравнения состояния Ван дер Ваальса без сингулярности при $v = b$ . Теоретически второй вириальный коэффициент представляет собой бимолекулярные силы притяжения, а третий вириальный член представляет собой силы отталкивания между тремя молекулами, находящимися в тесном контакте. ^{[ нужна ссылка ]}

С помощью этого кубического вириального уравнения коэффициенты B и C можно решить в замкнутой форме. Наложение критических условий: ${\frac {\mathrm {d} P}{\mathrm {d} v}}=0\qquad {\text{and}}\qquad {\frac {\mathrm {d} ^{2}P}{\mathrm {d} v^{2}}}=0$ кубическое уравнение вириала можно решить и получить: $B=-v_{c},$ $C={\frac {v_{c}^{2}}{3}},$ и $Z_{c}={\frac {P_{c}v_{c}}{RT_{c}}}={\frac {1}{3}}.$ $Z_{c}$ следовательно, составляет 0,333 по сравнению с 0,375 из уравнения Ван-дер-Ваальса.

Между критической точкой и тройной точкой находится область насыщения флюидами. В этой области газовая фаза сосуществует с жидкой фазой под давлением насыщения. $P_{\text{sat}}$ , а температура насыщения $T_{\text{sat}}$ . Под давлением насыщения жидкая фаза имеет молярный объем $v_{\text{l}}$ , а газообразная фаза имеет молярный объем $v_{\text{g}}$ . Соответствующие молярные плотности равны $\rho _{\text{l}}$ и $\rho _{\text{g}}$ . Это свойства насыщения, необходимые для вычисления второго и третьего вириальных коэффициентов.

Действительное уравнение состояния должно давать изотерму, пересекающую горизонтальную линию $P_{\text{sat}}$ в $v_{\text{l}}$ и $v_{\text{g}}$ , на $T_{\text{sat}}$ . ^{[ нужна ссылка ]} Под $P_{\text{sat}}$ и $T_{\text{sat}}$ , газ находится в равновесии с жидкостью. Это означает, что изотерма PρT имеет три корня при $P_{\text{sat}}$ . Кубическое вириальное уравнение состояния при $T_{\text{sat}}$ является: $P_{\text{sat}}=RT_{\text{sat}}\left(1+B\rho +C\rho ^{2}\right)\rho$ Его можно переставить так: $1-{\frac {RT_{\text{sat}}}{P_{\text{sat}}}}\left(1+B\rho +C\rho ^{2}\right)\rho =0$ Фактор $RT_{\text{sat}}/P_{\text{sat}}$ - это объем насыщенного газа согласно закону идеального газа, которому может быть присвоено уникальное имя. $v^{\text{id}}$ : $v^{\text{id}}={\frac {RT_{\text{sat}}}{P_{\text{sat}}}}$ В области насыщения кубическое уравнение имеет три корня и альтернативно может быть записано как: $\left(1-v_{\text{l}}\rho \right)\left(1-v_{\text{m}}\rho \right)\left(1-v_{\text{g}}\rho \right)=0$ который можно расширить как: $1-\left(v_{\text{l}}+v_{\text{g}}+v_{m}\right)\rho +\left(v_{\text{l}}v_{\text{g}}+v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)\rho ^{2}-v_{\text{l}}v_{\text{g}}v_{\text{m}}\rho ^{3}=0$ $v_{\text{m}}$ представляет собой объем неустойчивого состояния между $v_{\text{l}}$ и $v_{\text{g}}$ . Кубические уравнения идентичны. Следовательно, из линейных членов в этих уравнениях $v_{m}$ можно решить: $v_{\text{m}}=v^{\text{id}}-v_{\text{l}}-v_{\text{g}}$ Из квадратичных членов B можно решить: $B=-{\frac {\left(v_{\text{l}}v_{\text{g}}+v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)}{v^{\text{id}}}}$ А из кубических членов C можно решить: $C={\frac {v_{\text{l}}v_{\text{g}}v_{\text{m}}}{v^{\text{id}}}}$ С $v_{\text{l}}$ , $v_{\text{g}}$ и $P_{\text{sat}}$ были сведены в таблицы для многих жидкостей с $T_{\text{sat}}$ В качестве параметра B и C можно рассчитать в области насыщения этих жидкостей. Результаты в целом согласуются с результатами, рассчитанными на основе уравнений состояния Бенедикта-Уэбба-Рубина и Старлинга. ^{[ нужна ссылка ]}

См. также

Ссылки

^ Камерлинг Оннес Х., Выражение состояния газов и жидкостей с помощью серий, KNAW Proceedings, 4, 1901–1902, Амстердам, 125–147 (1902).
^ Даймонд Дж. Д., Уилхойт Р. К., Вириальные коэффициенты чистых газов и смесей, Springer (2003).
^ Даймонд Дж. Х., Смит Э. Б., Вириальные коэффициенты чистых газов и смесей. Критический сборник, Oxford University Press, 1-е издание (1969 г.), 2-е издание (1980 г.).
^ «Двигатель Термоданных» .
^ «Сетевые термотаблицы NIST/TRC (WTT): критически оцененные данные о теплофизических свойствах» .
^ Ван дер Ваальс Дж. Д., О непрерывности газообразного и жидкого состояний (Докторская диссертация). Лейденский университет (1873 г.).
^ Дитеричи (7), К. Дитеричи, Энн. Физ. хим. Видеманс Анн. 69, 685 (1899).
^ Д. Бертло, Д., в трудах и мемуарах Международного бюро мер и весов - Том XIII (Париж: Готье-Виллар, 1907).
^ Редлих, Отто; Квонг, JNS. О термодинамике растворов, Chem. Откр. 44 (1): 233–244 (1949).
^ Пэн, ДЮ; Робинсон, Д.Б., Новое двухконстантное уравнение состояния. Промышленная и техническая химия: Основы. 15: 59–64 (1976).
^ Битти, Дж. А., и Бриджман, О. К., Новое уравнение состояния жидкостей, Proc. Являюсь. акад. Art Sci., 63, 229–308 (1928).
^ Бенедикт, Мэнсон; Уэбб, Джордж Б.; Рубин, Луи К., Эмпирическое уравнение термодинамических свойств легких углеводородов и их смесей: I. Метан, этан, пропан и н-бутан, Журнал химической физики, 8 (4): 334–345 (1940).
^ Jump up to: ^а ^б Старлинг, Кеннет Э., Свойства жидкости для систем легкой нефти, Gulf Publishing Company, стр. 270 (1973).

[onnes-1] Камерлинг Оннес Х., Выражение состояния газов и жидкостей с помощью серий, KNAW Proceedings, 4, 1901–1902, Амстердам, 125–147 (1902).

[2] Даймонд Дж. Д., Уилхойт Р. К., Вириальные коэффициенты чистых газов и смесей, Springer (2003).

[3] Даймонд Дж. Х., Смит Э. Б., Вириальные коэффициенты чистых газов и смесей. Критический сборник, Oxford University Press, 1-е издание (1969 г.), 2-е издание (1980 г.).

[4] «Двигатель Термоданных» .

[5] «Сетевые термотаблицы NIST/TRC (WTT): критически оцененные данные о теплофизических свойствах» .

[6] Ван дер Ваальс Дж. Д., О непрерывности газообразного и жидкого состояний (Докторская диссертация). Лейденский университет (1873 г.).

[7] Дитеричи (7), К. Дитеричи, Энн. Физ. хим. Видеманс Анн. 69, 685 (1899).

[8] Д. Бертло, Д., в трудах и мемуарах Международного бюро мер и весов - Том XIII (Париж: Готье-Виллар, 1907).

[9] Редлих, Отто; Квонг, JNS. О термодинамике растворов, Chem. Откр. 44 (1): 233–244 (1949).

[10] Пэн, ДЮ; Робинсон, Д.Б., Новое двухконстантное уравнение состояния. Промышленная и техническая химия: Основы. 15: 59–64 (1976).

[11] Битти, Дж. А., и Бриджман, О. К., Новое уравнение состояния жидкостей, Proc. Являюсь. акад. Art Sci., 63, 229–308 (1928).

[12] Бенедикт, Мэнсон; Уэбб, Джордж Б.; Рубин, Луи К., Эмпирическое уравнение термодинамических свойств легких углеводородов и их смесей: I. Метан, этан, пропан и н-бутан, Журнал химической физики, 8 (4): 334–345 (1940).

[starling-13] Jump up to: ^а ^б Старлинг, Кеннет Э., Свойства жидкости для систем легкой нефти, Gulf Publishing Company, стр. 270 (1973).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]