Уравнение Ван дер Ваальса

Уравнение Ван дер Ваальса , названное в честь его создателя, голландского физика Йоханнеса Дидерика ван дер Ваальса , представляет собой уравнение состояния , которое расширяет закон идеального газа , включив в него ненулевой размер молекул газа и взаимодействия между ними (оба из которых зависят от конкретного вещества). результате уравнение способно моделировать фазовый переход жидкости В $\leftrightarrow$ пар . Он также дает простые аналитические выражения для свойств реальных веществ, которые проливают свет на их поведение. Один из способов записи этого уравнения: $$p={\frac {RT}{v-b}}-{\frac {a}{v^{2}}}$$где $p$ это давление , $T$ это температура , а $v=VN_{\text{A}}/N$ объём молярный , $N_{\text{A}}$ – постоянная Авогадро , $V$ это объем , и $N$ – число молекул (отношение $N/N_{\text{A}}$ — физическая величина с базовой единицей моль в системе СИ ). Кроме того $R=N_{\text{A}}k$ — универсальная газовая постоянная , $k$ – постоянная Больцмана и $a$ и $b$ являются экспериментально определяемыми константами, специфичными для вещества.

Сила действия одной молекулы на другую, находящуюся на расстоянии $r$ является отрицательным наклоном этой кривой при $r$. Сила отталкивающая и большая, поскольку $r<\sigma$и привлекательным, когда $r>r_{0}>\sigma$.

Константа $a$ выражает силу молекулярных взаимодействий. Его размерность давление умножена на квадрат молярного объема, [pv ² ], что также равно молярной энергии, умноженной на мольный объем. Константа $b$ обозначает исключенный молярный объем из-за конечного размера молекулы, поскольку центры двух молекул не могут быть ближе, чем их диаметр, $\sigma$. Теоретический расчет этих констант для сферических молекул с межчастичным потенциалом, характеризующимся $\sigma$, и минимальная энергия, $-\varepsilon$, как показано на прилагаемом графике, дает $b=4[4\pi (\sigma /2)^{3}/3]N_{\text{A}}$. Умножив это на количество родинок, $N/N_{\text{A}}$, дает исключенный объем, равный 4-кратному объему всех молекул. Эта теория также производит $a=I\varepsilon N_{\text{A}}b$ где $I$ – число, зависящее от формы потенциальной функции, $\varphi (r)$.

В своей книге (см. ссылки [3] и [4]) Больцман написал уравнения, используя $V/M$ ( удельный объем ) вместо $VN_{\text{A}}/N$ (молярный объем), использованный здесь, Гиббс тоже, как и большинство инженеров. Также имущество, $V/N$ обратная числовой плотности, используется физиками, но нет существенной разницы между уравнениями, записанными с любым из этих свойств. Уравнения состояния, записанные с использованием молярного объема, содержат $R$, те, которые используют определенный объем, содержат $R/{\bar {m}}$ (специфическое вещество ${\bar {m}}$ — молярная масса ), а написанные с числовой плотностью содержат $k$.

Один раз $a$ и $b$ определяются экспериментально для данного вещества, уравнение Ван-дер-Ваальса можно использовать для прогнозирования температуры кипения при любом заданном давлении, критической точки (определяемой значениями давления и температуры, $p_{\text{c}}$, $T_{\text{c}}$ такое, что вещество не может быть сжижено ни при $p>p_{\text{c}}$ независимо от того, насколько низка температура или когда $T>T_{\text{c}}$ независимо от того, насколько велико давление) и другие атрибуты. Эти предсказания точны лишь для нескольких веществ. Для большинства простых жидкостей они являются лишь ценным приближением. Уравнение также объясняет, почему перегретые жидкости могут существовать выше точки кипения, а переохлажденные пары могут существовать ниже точки конденсации.

График справа представляет собой график $T$ против $v$ рассчитывается по уравнению для четырех постоянных значений давления. На красной изобаре $p=2p_{\text{c}}$наклон положителен во всем диапазоне, $b\leq v<\infty$ (хотя на графике показан только конечный квадрант). Это описывает жидкость как газ для всех $T$, и характерно для всех изобар $p>p_{\text{c}}.$ Зеленая изобара, $p=0.2\,p_{\text{c}}$, имеет физически нереальный отрицательный наклон, поэтому показан пунктирным серым цветом между локальным минимумом, $T_{\rm {min}},v_{\rm {min}}$, и локальный максимум, $T_{\rm {max}},v_{\rm {max}}$. Это описывает жидкость как две несвязанные ветви; газ для $v\geq v_{\rm {min}}$и более плотная жидкость для $v\leq v_{\rm {max}}\leq v_{\rm {min}}$.

Термодинамические требования механического, теплового и материального равновесия вместе с уравнением определяют две точки на кривой: $(T_{s},v_{f})$, и $(T_{s},v_{g})$, показанные зелеными кружками, которые обозначают сосуществующую кипящую жидкость и конденсирующийся газ соответственно. Нагрев жидкости в этом состоянии увеличивает долю газа в смеси; его $v$, в среднем $v_{f}$ и $v_{g}$ взвешенный по этой дроби, увеличивается, в то время как $T_{s}$ остается прежним. Это показано пунктирной серой линией, поскольку оно не представляет собой решение уравнения; однако он описывает наблюдаемое поведение. Пункты выше $T_{s}$, перегретая жидкость, и находящиеся под ней, переохлажденный пар, метастабильны; достаточно сильное возмущение заставляет их перейти к устойчивой альтернативе. Поэтому они показаны пунктиром. Наконец, точки в области отрицательного наклона неустойчивы. Все это описывает жидкость как стабильный газ для $T>T_{\text{s}}$, стабильная жидкость для $T<T_{\text{s}}$, и смесь жидкости и газа при $T=T_{\text{s}}$, что также поддерживает метастабильные состояния недогретого газа и перегретой жидкости. Характерно для всех изобар. $0<p<p_{\text{c}}$, где $T_{\text{s}}$ является функцией $p$. Оранжевая изобара является критической, на которой минимум и максимум равны. Черная изобара — это предел положительных давлений, хотя нарисованная сплошной линией ни одна из ее точек не представляет собой устойчивых решений, они либо метастабильны (положительный или нулевой наклон), либо неустойчивы (отрицательный наклон). Все это является хорошим объяснением наблюдаемого поведения жидкостей.

с законом

Закон идеального газа следует из уравнения Ван-дер-Ваальса всякий раз, когда $v$ достаточно велика (или, соответственно, всякий раз, когда молярная плотность, $\rho =1/v$, достаточно мало), в частности

• когда $v\gg b$, затем $v-b$ численно неотличим от $v$,
• и когда $v\gg (a/p)^{1/2}$, затем $p+a/v^{2}$ численно неотличим от $p$.

Подставляя эти два приближения в уравнение Ван-дер-Ваальса, когда $v$ достаточно велико, чтобы удовлетворялись оба неравенства, сводит его к $$p=RT/v\quad {\mbox{or in terms of }}V{\mbox{ and }}N\quad pV=NkT$$что является законом идеального газа. Это неудивительно, поскольку уравнение Ван-дер-Ваальса было построено на основе уравнения идеального газа, чтобы получить уравнение, действительное за пределами поведения идеального газа.

Что действительно примечательно, так это степень успеха Ван дер Ваальса. Действительно, Эпштейн в своем классическом учебнике по термодинамике начал обсуждение уравнения Ван-дер-Ваальса со слов: «Несмотря на его простоту, оно охватывает как газообразное, так и жидкое состояние и самым замечательным образом выявляет все явления, относящиеся к к непрерывности этих двух государств». Также в пятом томе своих «Лекций по теоретической физике» Зоммерфельд , помимо того, что отмечает, что «Больцманн описал Ван-дер-Ваальса как Ньютона реальных газов », а также написал: «Очень примечательно, что теория Ван-дер-Ваальса способна предсказать, по крайней мере качественно, нестабильность [имеется в виду перегретая жидкость и переохлажденный пар, который сейчас называемые метастабильными] состояниями», которые связаны с процессом изменения фазы.

Полезность уравнения

Уравнение было и остается очень полезным, потому что:

• Его коэффициент теплового расширения, $\alpha =(\partial _{T}v|_{p})/v$ имеет простое аналитическое выражение (это справедливо и для его изотермической сжимаемости, $\kappa _{T}=-(\partial _{p}v|_{T})/v$]
• это объясняет существование критической точки жидкость–пар, и фазового перехода включая наблюдаемые метастабильные состояния.
• он устанавливает право соответствующих государств
• его удельная теплоемкость при постоянном объеме, $c_{v}$, можно показать как функцию $T$ только и его термодинамические свойства, внутренняя энергия $u$, энтропия $s$, а также теплоемкость при постоянном давлении $c_{p}$ имеют простые аналитические выражения [это справедливо и для энтальпии $h=u+pv$, свободная энергия Гельмгольца $f=u-Ts$и свободная энергия Гиббса $g=u+pv-Ts=f+pv=h-Ts$]
• его коэффициент Джоуля-Томсона и связанная с ним кривая инверсии, которые сыграли важную роль в коммерческом сжижении газов, имеют простые аналитические выражения.

Уравнение также играет важную роль в современной теории фазовых переходов. Он количественно изображает жидкие металлы, Меркурий и Цезий, и качественно описывает большинство реальных жидкостей. Следовательно, его можно рассматривать как одного из членов семейства уравнений состояния, которые зависят от молекулярного параметра, такого как критический коэффициент сжимаемости, $Z_{\text{c}}=p_{\text{c}}v_{\text{c}}/(RT_{\text{c}})$, или фактор Питцера ( ацентрический ), $\omega =-\log[p_{s}(T/T_{\text{c}}=0.7)/p_{\text{c}}]-1$, где $p_{s}/p_{\text{c}}=p_{s}(T/T_{\text{c}},\omega )$ – безразмерное давление насыщения, log – логарифм по основанию 10.

Все это делает ее ценным педагогическим инструментом для преподавателей физики, химии и инженерного дела, а также полезной математической моделью, которая может помочь студентам в понимании.

История

В 1857 году Рудольф Клаузиус опубликовал «Природу движения, которое мы называем теплом» . В нем он вывел соотношение $p=nm{\overline {v^{2}}}/3$ для давления, $p$, в газе с $n$ частицы в единице объема (числовая плотность), масса $m$, и средняя квадратичная скорость ${\overline {v^{2}}}$. Затем он заметил, что, используя классические законы Бойля и Чарльза, можно написать $m{\overline {v^{2}}}/3=kT$ с $k$ константа пропорциональности. Следовательно, температура была пропорциональна средней кинетической энергии частиц. Эта статья вдохновила на дальнейшую работу, основанную на двойственной идее о том, что вещества состоят из неделимых частиц и что тепло является следствием движения частиц, подчиняющегося законам Ньютона. Работа, известная как кинетическая теория газов , была выполнена главным образом Клаузиусом, Джеймсом Клерком Максвеллом и Людвигом Больцманом. Примерно в то же время Дж. Уиллард Гиббс также внес свой вклад и развил ее, превратив ее в статистическую механику .

Уравнение Ван дер Ваальса на стене в Лейдене

Эта среда оказала влияние на Йоханнеса Дидерика ван дер Ваальса. Первоначально получив преподавательскую степень, он был принят в докторантуру Лейденского университета под руководством Питера Рийке . Это привело в 1873 году к диссертации, в которой было предложено простое уравнение на основе частиц, описывающее изменение состояния газа и жидкости, происхождение критической температуры и концепцию соответствующих состояний. Уравнение основано на двух предпосылках: во-первых, жидкости состоят из частиц с ненулевыми объемами, а во-вторых, на достаточно большом расстоянии каждая частица оказывает силу притяжения на все другие частицы в ее окрестностях. Эти силы были названы Больцманом ван дер Ваальсом связующими силами .

В 1869 году ирландский профессор химии Томас Эндрюс из Королевского университета в Белфасте в статье, озаглавленной « О непрерывности газообразного и жидкого состояний вещества» , продемонстрировал экспериментально полученный набор изотерм угольной кислоты H $_{2}$СО $_{3}$, показавший при низких температурах скачок плотности при определенном давлении, а при более высоких температурах резкого изменения не наблюдалось; рисунок можно увидеть здесь . Критической точкой Эндрюс назвал изотерму, при которой скачок только что исчез. Учитывая сходство названий этой статьи и последующей диссертации Ван дер Ваальса, можно подумать, что Ван дер Ваальс намеревался разработать теоретическое объяснение экспериментов Эндрюса. Однако верно и обратное: Ван дер Ваальс начал работу с попытки определить молекулярное притяжение, возникшее в теории капиллярности Лапласа, и только после установления своего уравнения проверил его, используя результаты Эндрюса.

К 1877 году были созданы распылители жидкого кислорода и жидкого азота новая область исследований — физика низких температур , и была открыта . Во всем этом сыграло роль уравнение Ван-дер-Ваальса, особенно в отношении сжижения водорода и гелия, которое наконец было достигнуто в 1908 году. Из измерений $p_{1},T_{1}$ и $p_{2},T_{2}$ в двух состояниях с одинаковой плотностью уравнение Ван-дер-Ваальса дает значения $b=v-R(T_{2}-T_{1})/(p_{2}-p_{1})]$ и $a=v^{2}(p_{2}T_{1}-p_{1}T_{2})/(T_{2}-T_{1})$. Таким образом, из двух таких измерений давления и температуры можно было определить $a$ и $b$, и на основе этих значений вычисляют ожидаемое критическое давление, температуру и молярный объем. Гудштейн резюмировал этот вклад уравнения Ван-дер-Ваальса следующим образом:

Весь этот труд требовал значительной веры в то, что все газожидкостные системы по сути одинаковы, даже если никто никогда не видел жидкую фазу. Эта вера возникла в результате неоднократного успеха теории Ван дер Ваальса, которая, по сути, представляет собой универсальное уравнение состояния, независимое от деталей какого-либо конкретного вещества после его правильного масштабирования. ... В результате не только можно было поверить, что водород можно сжижать. но можно было даже предсказать необходимую температуру и давление.

Ван дер Ваальсу была присуждена Нобелевская премия в 1910 году в знак признания вклада в формулировку «уравнения состояния газов и жидкостей».

Как отмечалось ранее, современные исследования фазовых переходов первого порядка используют уравнение Ван-дер-Ваальса вместе с критерием Гиббса, равным химическому потенциалу каждой фазы, в качестве модели явления. Эта модель имеет аналитическую кривую сосуществования (насыщения), выраженную параметрически: $p_{s}=f_{p}(y),T_{s}=f_{T}(y)$, впервые полученное Планком, известный Гиббсу, а позже полученный Лекнером в красивой простой и элегантной манере. Краткое изложение решения Лекнера представлено в следующем разделе, а более полное обсуждение — в конструкции Максвелла .

точка и

На рисунке 1 показаны четыре изотермы уравнения Ван-дер-Ваальса (сокращенно vdW) на плоскости давления и молярного объема. Существенный характер этих кривых заключается в том, что:

Рисунок 1: Четыре изотермы уравнения Ван-дер-Ваальса, а также спинодальная кривая с черной штриховой точкой и кривая сосуществования (насыщения) с красной штриховой точкой, построенная с использованием приведенных (безразмерных) переменных.

1. при некоторой критической температуре, $T=T_{\text{c}}$ наклон отрицательный, $\partial p/\partial v|_{T}<0$, везде, кроме одной точки, критической точки, $p=p_{\text{c}},v=v_{\text{c}}$, где наклон и кривизна равны нулю, $\partial p/\partial v|_{T}=\partial ^{2}p/\partial v^{2}|_{T}=0$;
2. при более высоких температурах наклон изотерм всюду отрицательный (значения $p,T$ для которого уравнение имеет 1 вещественный корень при $v$);
3. при более низких температурах на каждой изотерме имеются две точки, где наклон равен нулю (значения $p$, $T$ для которого уравнение имеет 3 действительных корня при $v$)

Оценка двух частных производных в 1) с использованием уравнения ВДВ и приравнивание их нулю дает: $v_{\text{c}}=3b,T_{\text{c}}=8a/(27Rb)$, и использование их в уравнении дает $p_{\text{c}}=a/27b^{2}$.

Этот расчет можно выполнить алгебраически, заметив, что уравнение ВДВ можно записать в виде кубики. $v$, что в критической точке: $p_{\text{c}}cv^{3}-(p_{\text{c}}b+RT_{\text{c}})v^{2}+av-ab=0$. Более того, в критической точке все три корня сливаются, поэтому это также можно записать как $$(v-v_{\text{c}})^{3}=v^{3}-3v_{\text{c}}v^{2}+3v_{\text{c}}^{2}v-v_{\text{c}}^{3}=0$$Затем разделив первое на $p_{\text{c}}$и учитывая, что эти два кубических уравнения одинаковы, когда все их коэффициенты равны, получаем три уравнения $$b+RT_{\text{c}}/p_{\text{c}}=3v_{\text{c}}\quad a/p_{\text{c}}=3v_{\text{c}}^{2}\quad ab/p_{\text{c}}=v_{\text{c}}^{3}$$ решение которого дает предыдущие результаты для $p_{\text{c}},v_{\text{c}},T_{\text{c}}$.

Использование этих критических значений для определения приведенных свойств $p_{r}=p/p_{\text{c}},T_{r}=T/T_{\text{c}},v_{r}=v/v_{\text{c}}$ приводит уравнение в безразмерный вид, использованный для построения рис. 1 $$p_{r}={\frac {8T_{r}}{3v_{r}-1}}-{\frac {3}{v_{r}^{2}}}$$Эта безразмерная форма является отношением подобия; это указывает на то, что все жидкости VdW одновременно $T_{r}$ будет построен на той же кривой. Он выражает закон соответствующих состояний , который Больцман описал следующим образом:

Из этого уравнения выпали все константы, характеризующие газ. Если кто-то основывает измерения на единицах Ван-дер-Ваальса (название Больцмана для приведенных здесь величин), то он получает одно и то же уравнение состояния для всех газов. ... Только значения критического объема, давления и температуры зависят от природы конкретного вещества; числа, которые выражают фактический объем, давление и температуру как кратные критическим значениям, удовлетворяют одному и тому же уравнению для всех веществ. Другими словами, одно и то же уравнение связывает приведенный объем, приведенное давление и приведенную температуру для всех веществ.

Очевидно, что такое широкое общее отношение вряд ли будет правильным; тем не менее, весьма примечательно то, что с его помощью можно получить по существу правильное описание реальных явлений.

Этот «закон» — всего лишь частный случай размерного анализа , в котором уравнение, содержащее шестимерные величины, $p,v,T,a,b,R$и 3 измерения, [p], [v], [T], должны быть выражены через 6 − 3 = 3 безразмерные группы. Здесь $v^{*}=b$ - характерный молярный объем, $p^{*}=a/b^{2}$ характерное давление и $T^{*}=a/(Rb)$ характеристическая температура, а 3 безразмерные группы: $p/p^{*},v/v^{*},T/T^{*}$. Приведенные свойства, определенные ранее: $p_{r}=27(p/p^{*})$, $v_{r}=(1/3)(v/v^{*})$, и $T_{r}=(27/8)(T/T^{*})$. Недавние исследования показали, что существует семейство уравнений состояния, зависящих от дополнительной безразмерной группы, и это обеспечивает более точную корреляцию свойств. Тем не менее, как заметил Больцман, уравнение Ван-дер-Ваальса дает по существу правильное описание.

Уравнение ВДВ дает $Z_{\text{c}}=p_{\text{c}}v_{\text{c}}/(RT_{\text{c}})=3/8$, тогда как для большинства реальных жидкостей $0.23<Z_{\text{c}}<0.31$. Таким образом, большинство реальных жидкостей не удовлетворяют этому условию, и, следовательно, их поведение только качественно описывается уравнением ВДВ. Однако уравнение состояния ВДВ является членом семейства уравнений состояния, основанных на факторе Питцера ( ацентрическом ), $\omega$, а жидкие металлы, Меркурий и Цезий, хорошо им соответствуют.

Термодинамические свойства

Свойства молярная внутренняя энергия, $u$и энтропия, $s$, определяемый первым и вторым законами термодинамики, а следовательно, и все термодинамические свойства простого сжимаемого вещества, могут быть заданы с точностью до константы интегрирования двумя измеримыми функциями - механическим уравнением состояния, $p=p(v,T)$, и постоянная объемная удельная теплоемкость, $c_{v}(v,T)$.

Внутренняя энергия и удельная теплоемкость

Внутренняя энергия определяется энергетическим уравнением состояния: $$u-C_{u}=\int \,c_{v}(v,T)\,dT+\int \,\left[T{\frac {\partial p}{\partial T}}-p(v,T)\right]\,dv=\int \,c_{v}(v,T)\,dT+\int \,\left[T^{2}{\frac {\partial (p/T)}{\partial T}}\right]\,dv$$где $C_{u}$ – произвольная константа интегрирования.

Теперь, чтобы $du(v,T)$ быть точным дифференциалом, а именно, что $u(v,T)$ быть непрерывным с непрерывными частными производными, его вторые смешанные частные производные также должны быть равны, $\partial _{vT}^{2}u=\partial _{Tv}^{2}u$. Затем с $c_{v}=\partial _{T}u$ это условие можно записать просто как $\partial _{v}c(v,T)=\partial _{T}[T^{2}\partial _{T}(p/T)]$. Дифференциация $p/T$ для уравнения ВДВ дает $T^{2}\partial _{T}(p/T)]=a/v^{2}$, так $\partial _{v}c_{v}=0$. Следовательно $c_{v}=c_{v}(T)$ для жидкости ВДВ точно так же, как и для идеального газа. Для простоты здесь это считается константой, $c_{v}=cR$ с $c$ номер. Тогда оба интеграла можно легко вычислить, и результат будет равен $$u-C_{u}=cRT-a/v$$Это энергетическое уравнение состояния идеальной жидкости ВДВ. Проведя анализ размерностей (что можно было бы назвать распространением принципа соответствующих состояний на другие термодинамические свойства), его можно просто записать в сокращенной форме как $$u_{r}-{\mbox{C}}_{u}=cT_{r}-9/(8v_{r})$$где $u_{r}=u/(RT_{\text{c}})$ и С $_{u}$ является безразмерной константой.

Энтальпия

Энтальпия ​ ​ $h=u+pv$, и продукт $pv$ это просто $pv=RTv/(v-b)-a/v$. Затем $h$ это просто $$h-C_{u}=RT[c+v/(v-b)]-2a/v$$Это энтальпийное уравнение состояния идеальной жидкости ВДВ или в сокращенной форме. $$h_{r}-{\mbox{C}}_{u}=[c+3v_{r}/(3v_{r}-1)]T_{r}-9/(4v_{r})\quad {\mbox{where}}\quad h_{r}=h/(RT_{\text{c}}c)$$

Энтропия

Энтропия : определяется энтропийным уравнением состояния $$s-C_{s}=\int \,c_{v}(T)\,{\frac {dT}{T}}+\int \,{\frac {\partial p}{\partial T}}\,dv$$С использованием $c_{v}=cR$ как и раньше, и интегрируя второй член с помощью $\partial _{T}p=R/(v-b)$ мы получаем просто $$s-C_{s}=R\ln[T^{c}(v-b)]$$Это энтропийное уравнение состояния идеальной жидкости ВДВ или в сокращенной форме. $$s_{r}-{\mbox{C}}_{s}=\ln[T_{r}^{c}(3v_{r}-1)]$$

Свободная энергия Гиббса

– Свободная энергия Гиббса это $g=h-Ts$ поэтому объединение предыдущих результатов дает $$g-C_{u}=\{c+v/(v-b)-C_{s}-\ln[T^{c}(v-b)]\}RT-2a/v$$Это свободная энергия Гиббса для идеальной жидкости ВДВ или в приведенной форме. $$g_{r}-{\mbox{C}}_{u}=\{c+3v_{r}/(3v_{r}-1)-{\mbox{C}}_{s}-\ln[T_{r}^{c}(3v_{r}-1)]\}T_{r}-9/(4v_{r})$$

Термодинамические производные: α , κ _T и c _p

Две первые частные производные уравнения ВДВ: $${\frac {\partial p}{\partial T}}={\frac {R}{v-b}}\quad {\mbox{and}}\quad {\frac {\partial p}{\partial v}}=-{\frac {RT}{(v-b)^{2}}}+{\frac {2a}{v^{3}}}$$Первое уравнение $\alpha /\kappa _{T}$, а второй $-(v\kappa _{T})^{-1}$, где $\kappa _{T}=-v^{-1}\partial _{p}v$, изотермическая сжимаемость, является мерой относительного увеличения объема при повышении давления при постоянной температуре, в то время как $\alpha =v^{-1}\partial _{T}v_{p}$, коэффициент теплового расширения, является мерой относительного увеличения объема при повышении температуры при постоянном давлении. Поэтому $$\kappa _{T}={\frac {v^{2}(v-b)^{2}}{RTv^{3}-2a(v-b)^{2}}}\quad {\mbox{and}}\quad \alpha ={\frac {Rv^{2}(v-b)}{RTv^{3}-2a(v-b)^{2}}}$$В пределе $v\rightarrow \infty$ $\alpha =1/T$ пока $\kappa _{T}=v/(RT)$. Поскольку уравнение ВДВ в этом пределе принимает вид $p=RT/v$, окончательно $\kappa _{T}=1/p$. Оба эти значения являются значениями идеального газа, что соответствует, поскольку, как отмечалось ранее, в этом пределе жидкость ВДВ ведет себя как идеальный газ.

Удельная теплоемкость при постоянном давлении, $c_{p}$ определяется как частная производная $c_{p}=\partial _{T}h|_{p}$. Однако оно не является независимым от $c_{v}$, они связаны уравнением Майера , $c_{p}-c_{v}=-T(\partial _{T}p)^{2}/\partial _{v}p=Tv\alpha ^{2}/\kappa _{T}$. Тогда две части уравнения ВДВ можно использовать для выражения $c_{p}$ как $$c_{p}(v,T)-c_{v}(T)={\frac {R^{2}Tv^{3}}{RTv^{3}-2a(v-b)^{2}}}\geq R$$Здесь в пределе $v\rightarrow \infty$, $c_{p}-c_{v}=R$, что, как и ожидалось, также является результатом идеального газа; однако предел $v\rightarrow b$ дает тот же результат, что не согласуется с экспериментами на жидкостях.

В этом пределе жидкости мы также находим $\alpha =\kappa _{T}=0$, а именно, что жидкость ВДВ несжимаема. Более того, поскольку $\partial _{T}p=-\partial _{T}v/\partial _{p}v=\alpha /\kappa _{T}=\infty$, он также механически несжимаем, т.е. $\kappa _{T}\rightarrow 0$ быстрее, чем $\alpha$.

Окончательно $c_{p},\alpha$, и $\kappa _{T}$ все бесконечны на кривой $T=2a(v-b)^{2}/(Rv^{3})=T_{\text{c}}(3v_{r}-1)^{2}/(4v_{r}^{3})$. Эта кривая, называемая спинодальной кривой, определяется формулой $\kappa _{T}^{-1}=0$и подробно обсуждается в следующем разделе.

Стабильность

Согласно экстремальному принципу термодинамики $dS=0$ и $d^{2}S<0$, а именно, что в состоянии равновесия энтропия максимальна. Это приводит к требованию, чтобы $\partial p/\partial v|_{T}<0$. Этот математический критерий выражает физическое состояние, которое Эпштейн описал следующим образом:

Рисунок 1 повторяется

«Очевидно, что эта средняя часть, отмеченная на наших кривых пунктиром (место нарушения требования, отмеченное серым штрихом на рис. 1 и повторенное здесь), не может иметь никакой физической реальности. В самом деле, представим себе жидкость в состоянии соответствующая этой части кривой содержится в теплопроводном вертикальном цилиндре, вершина которого образована поршнем. Поршень может скользить в цилиндре вверх и вниз, и мы прикладываем к нему груз, точно уравновешивающий давление газа. снимите с поршня немного веса, равновесия больше не будет, и он начнет двигаться вверх. Однако по мере движения объем газа увеличивается, а вместе с ним и его давление, действующее на поршень, увеличивается, сохраняя свое значение. Следовательно, поршень будет продолжать двигаться, а газ расширяться, пока не достигнет состояния, представленного максимумом изотермы. И наоборот, если мы добавим хоть немного к нагрузке сбалансированного поршня, газ увеличится. коллапс до состояния, соответствующего минимуму изотермы»

Пока на изотерме $T>T_{\text{c}}c$ это требование выполняется везде, поэтому все состояния являются газами, те состояния, которые находятся на изотерме, $T<T_{\text{c}}$ которые лежат между локальным минимумом, $v_{\rm {min}}$, и локальный максимум, $v_{\rm {max}}$, для чего $\partial p/\partial v|_{T}>0$ (показаны пунктирным серым на рис. 1), нестабильны и поэтому не наблюдаются. Это происхождение фазового перехода; есть диапазон $v_{\rm {min}}\leq v\leq v_{\rm {max}}$, для которого не существует наблюдаемых состояний. Штаты для $v<v_{\rm {min}}$ являются жидкими и для $v>v_{\rm {max}}>v_{\rm {min}}$ представляют собой пар; из-за силы тяжести более плотная жидкость находится под паром. Точки перехода, состояния с нулевым наклоном, называются точками спинодали. Их локусом является спинодальная кривая, отделяющая области плоскости, в которых существуют жидкость, пар и газ, от области, где не существует наблюдаемых состояний. Эта спинодальная кривая получается здесь из уравнения ВДВ путем дифференцирования (или, что то же самое, из $\kappa _{T}=\infty$) как $$T_{\rm {sp}}=2a{\frac {(v-b)^{2}}{Rv^{3}}}=T_{\text{c}}{\frac {(3v_{r}-1)^{2}}{4v_{r}^{3}}}\qquad p_{\rm {sp}}={\frac {a(v-2b)}{v^{3}}}=p_{\text{c}}{\frac {(3v_{r}-2)}{v_{r}^{3}}}$$Проекция этой пространственной кривой изображена на рис. 1 в виде черной штрихпунктирной кривой. Он проходит через критическую точку, которая также является точкой спинодали.

Насыщенность

Хотя разрыв в $v$ ограничен двумя спинодальными точками на изотерме ( например, $T_{r}=7/8$ показано на рис. 1) является источником фазового перехода, точки спинодали не отражают его полную протяженность, поскольку оба состояния, насыщенная жидкость и насыщенный пар, сосуществуют в равновесии; они оба должны иметь одинаковое давление и одинаковую температуру. Таким образом, характеризуется фазовый переход при температуре $T_{s}$, давлением $p_{\rm {min}}<p_{s}<p_{\rm {max}}$ которая лежит между минимальной и максимальной спинодальными точками и с молярными объемами жидкости, $v_{f}<v_{\rm {min}}$ и пар $v_{g}>v_{\rm {max}}$. Тогда из уравнения ВДВ, примененного к этим состояниям насыщенной жидкости и пара, $$p_{s}={\frac {RT_{s}}{v_{f}-b}}-{\frac {a}{v_{f}^{2}}}\quad {\mbox{and}}\quad p_{s}={\frac {RT_{s}}{v_{g}-b}}-{\frac {a}{v_{g}^{2}}}$$Эти два уравнения ВДВ содержат 4 переменные: $p_{\text{s}},T_{\text{s}},v_{f},v_{g}$, поэтому требуется другое уравнение, чтобы однозначно определить значения трех из этих переменных в терминах четвертой. Такое уравнение здесь обеспечивается равенством свободной энергии Гиббса в состояниях насыщенной жидкости и пара: $g_{f}=g_{g}$. Это условие материального равновесия можно получить из простого физического аргумента следующим образом: энергия, необходимая для испарения моля, определяется вторым законом при постоянной температуре. $q_{\rm {vap}}=T(s_{g}-s_{f})$, и из первого закона при постоянном давлении $q_{\rm {vap}}=h_{g}-h_{f}$. Приравнивая эти два, переставляя и вспоминая, что $g=h-Ts$ дает результат.

Свободная энергия Гиббса - это один из четырех термодинамических потенциалов, частные производные которого создают все другие свойства термодинамического состояния; его дифференциал $dg=\partial _{p}g\,dp+\partial _{T}g\,dT=v\,dp-s\,dT$. Интегрируя это по изотерме от $p_{s},v_{f}$ к $p_{s},v_{g}$, отметив, что давление одинаково в каждой конечной точке, и установив результат равным нулю, получим $$g_{g}-g_{f}=\sum _{j=1}^{3}\int _{p_{j}}^{p_{j}+1}\,v_{j}\,dp=-\int _{v_{f}}^{v_{g}}\,p\,dv+p_{s}(v_{g}-v_{f})=0$$Здесь потому что $v$ является многозначной функцией, то $p$ Интеграл необходимо разделить на 3 части, соответствующие 3 действительным корням уравнения ВДВ в виде: $v(p,T)$ (это легче всего представить себе, представив рис. 1 повернутым на 90°). $^{\circ }$); в результате получается частный случай материального равновесия. Последнее равенство, следующее из интегрирования $v\,dp=d(pv)-p\,dv$ Максвелла , является правилом равных площадей , которое требует, чтобы верхняя область между кривой ВДВ и горизонтальной линией $p_{\text{s}}$ быть равным нижнему. Эта форма означает, что термодинамическое ограничение, фиксирующее $p_{s}$ задается самим уравнением состояния, $p=p(v,T)$. Использование уравнения для свободной энергии Гиббса, полученного ранее для уравнения ВДВ, примененного к состоянию насыщенного пара, и вычитание результата, примененного к состоянию насыщенной жидкости, дает: $$RT_{s}\left[{\frac {v_{g}}{v_{g}-b}}-{\frac {v_{f}}{v_{f}-b}}-\ln \left({\frac {v_{g}-b}{v_{f}-b}}\right)\right]-2a\left({\frac {1}{v_{g}}}-{\frac {1}{v_{f}}}\right)=0$$Это третье уравнение, которое вместе с двумя приведенными выше уравнениями ВДВ можно решить численно. Это было сделано с учетом значения либо $T_{s}$ или $p_{s}$и представлены табличные результаты; однако уравнения допускают и аналитическое параметрическое решение, наиболее просто и изящно полученное Лекнером. Подробности этого решения можно найти в Maxwell Construction ; результаты $$T_{rs}(y)=\left({\frac {27}{8}}\right){\frac {2f(y)[\cosh y+f(y)]}{g(y)^{2}}}\quad p_{rs}=27{\frac {f(y)^{2}[1-f(y)^{2}]}{g(y)^{2}}}$$$$v_{rf}=\left({\frac {1}{3}}\right){\frac {1+f(y)e^{y}}{f(y)e^{y}}}\qquad \qquad \qquad \quad v_{rg}=\left({\frac {1}{3}}\right){\frac {1+f(y)e^{-y}}{f(y)e^{-y}}}$$где $$f(y)={\frac {y\cosh y-\sinh y}{\sinh y\cosh y-y}}\qquad \qquad g(y)=1+2f(y)\cosh y+f(y)^{2}$$

Рисунок 2: Черная пунктирная кривая представляет собой предел устойчивости (спинодальная кривая), а пунктирная синяя кривая представляет собой кривую сосуществования или насыщения, построенную на $p_{r},T_{r}$ самолет. В каждой точке области между двумя кривыми существуют два состояния: одно стабильное, а другое метастабильное. Метастабильные состояния — перегретая жидкость и переохлажденный пар — показаны пунктиром на рис. 1.

и параметр $0\leq y<\infty$ дается физически $y=(s_{g}-s_{f})/(2R)$. Значения всех других разрывов свойств на кривой насыщения также следуют из этого решения. Эти функции определяют кривую сосуществования, которая является местом расположения состояний насыщенной жидкости и насыщенного пара жидкости ВДВ. Кривая построена на рис. 1 и рис. 2, двух проекциях поверхности состояния. Эти кривые точно согласуются с численными результатами, упомянутыми ранее.

Возвращаясь к рис. 1, изотермы для $T_{r}<1$ являются прерывистыми. Учитывая $T_{r}=7/8$ например, он состоит из двух отдельных зеленых сегментов. Сплошной сегмент над зеленым кругом слева и ниже справа соответствует стабильным состояниям, точки представляют состояния насыщенной жидкости и пара, которые включают фазовый переход, а два зеленых пунктирных сегмента ниже и выше точек представляют собой метастабильные состояния, перегретая жидкость и переохлажденный пар , которые создаются в процессе фазового перехода, имеют короткое время жизни, а затем переходят в свою стабильную альтернативу с более низкой энергией.

В своем трактате 1898 года, в котором он очень подробно описал уравнение Ван-дер-Ваальса, Больцман обсуждал эти состояния в разделе, озаглавленном «Недоохлаждение, замедленное испарение»; теперь они обозначаются как переохлажденный пар и перегретая жидкость . Более того, теперь стало ясно, что эти метастабильные состояния регулярно возникают в процессе фазового перехода. В частности, процессы, сопровождающиеся очень высокими тепловыми потоками, создают большое количество этих состояний, и переход к их устойчивой альтернативе с соответствующим выделением энергии может быть опасным. В связи с этим возникает острая необходимость изучения их термических свойств.

В том же разделе Больцман также рассмотрел и объяснил отрицательное давление, которое проявляют некоторые жидкие метастабильные состояния (например, $T_{r}=0.8$ рис. 1). Он пришел к выводу, что такие жидкие состояния растягивающих напряжений были реальными, как это сделали Тьен и Линхард много лет спустя, которые написали: «Уравнение Ван-дер-Ваальса предсказывает, что при низких температурах жидкости выдерживают огромное напряжение... В последние годы были проведены измерения, которые выявили это. быть совершенно правым».

Несмотря на то, что фазовый переход приводит к математическому разрыву свойств однородной жидкости, например $v$, физического разрыва нет. Когда жидкость начинает испаряться, жидкость становится гетерогенной смесью жидкости и пара, молярный объем которой непрерывно изменяется от $v_{f}$ к $v_{g}$ по уравнению состояния $$v=v_{f}+x(v_{g}-v_{f})\qquad x=N_{g}/(N_{f}+N_{g})$$где $0\leq x\leq 1$ – мольная доля пара. Это уравнение называется правилом рычага и применимо и к другим свойствам. Состояния, которые оно представляет, образуют горизонтальную линию, соединяющую точки одного цвета на изотерме, но не показанную на рис. 1, как уже отмечалось, поскольку это отдельное уравнение состояния для гетерогенной комбинации компонентов жидкости и пара.

Ван дер

Рисунок 3: Семейство кривых насыщения, в котором кривая vdw является членом. Синие точки рассчитаны на основе решения Лекнера. Оранжевые точки рассчитаны на основе данных ASME Steam Tables Compact Edition, 2006.

Идея соответствующих состояний возникла, когда Ван дер Ваальс придал своему уравнению безразмерную форму: $p_{r}=p(v_{r},T_{r})$. Однако, как отмечал Больцман, такое простое представление не могло правильно описать все вещества. Действительно, анализ насыщения этой формы дает $p_{rs}=p_{s}(T_{r})$, а именно все вещества имеют одну и ту же безразмерную кривую сосуществования. Чтобы избежать этого парадокса, был предложен расширенный принцип соответствующих состояний, в котором $p_{r}=p(v_{r},T_{r},\phi )$ где $\phi$ — безразмерный параметр, зависящий от вещества, связанный с единственной физической характеристикой, связанной с отдельным веществом, — его критической точкой.

Первый кандидат на $\phi$ был критический коэффициент сжимаемости $Z_{\text{c}}=p_{\text{c}}v_{\text{c}}/(RT_{\text{c}})$, но поскольку эту величину трудно измерить точно, ацентрический фактор, разработанный Кеннетом Питцером, $\omega =-{\mbox{log}}_{10}[p_{r}(T_{r}=0.7)]-1$, более полезен. Давление насыщения в этой ситуации представлено однопараметрическим семейством кривых: $p_{rs}=p_{s}(T_{r},\omega )$. Ряд исследователей получили корреляции данных о насыщении для ряда веществ, лучшая из них — у Донга и Линхарда. $$\ln p_{rs}=5.37270(1-1/T_{r})+\omega (7.49408-11.181777T_{r}^{3}+3.68769T_{r}^{6}+17.92998\ln T_{r})$$

который имеет среднеквадратичную ошибку $\pm 0.42$ за пределами диапазона $1\leq T_{r}\leq 0.3$

Рисунок 4: График корреляции, включающий данные по различным веществам.

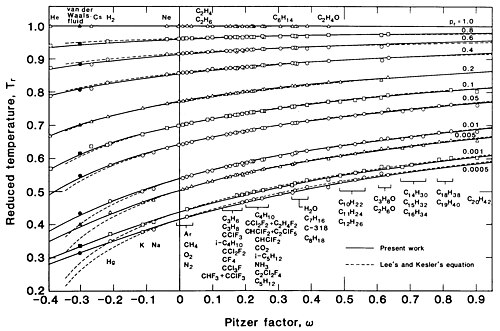
Рисунок 3 представляет собой график $p_{rs}$ против $T_{r}$. для различных значений $\omega$ как указано в этом уравнении. По оси ординат логарифмически показано поведение при давлениях, значительно ниже критического, где различия между различными веществами (обозначенные различными значениями $\omega$) более выражены.

Рисунок 4 представляет собой еще один график того же уравнения, показывающий $T_{r}$ как функция $\omega$ для различных значений $p_{rs}$. Он включает данные по 51 веществу, включая жидкость VdW, в диапазоне $-0.4<\omega <0.9$. Этот график ясно показывает, что жидкость VdW ( $\omega =-0.302$) принадлежит к классу реальных жидкостей; действительно, он количественно описывает поведение жидкого металла цезия ( $\omega =-0.267$) и ртуть ( $\omega =-0.21$), чьи значения $\omega$ близки к значению vdW. Однако он описывает поведение других жидкостей только качественно, поскольку конкретные числовые значения изменяются из-за различных значений их фактора Питцера, $\omega$.

Джоуля – Томсона и

Коэффициент Джоуля – Томсона, $\mu _{J}=\partial _{p}T|_{h}$, имеет практическое значение, поскольку два конечных состояния процесса регулирования ( $h_{2}=h_{1}$) лежат на кривой постоянной энтальпии. Хотя идеальные газы, для которых $h=h(T)$, не меняют температуру в таком процессе, как это делают реальные газы, и в приложениях важно знать, нагреваются они или остывают.

Этот коэффициент можно найти через ранее описанные производные как: $$\mu _{J}={\frac {v(\alpha T-1)}{c_{p}}}$$так что когда $\mu _{J}$ Положительное значение означает, что температура газа снижается при прохождении через дроссель, а если оно отрицательное, температура увеличивается. Поэтому условие $\mu _{J}=0$ определяет кривую, разделяющую область $T,p$ самолет, где $\mu _{J}>0$ из области, где оно меньше нуля. Эта кривая называется кривой инверсии, и ее уравнение имеет вид $\alpha T-1=0$. Используя выражение для $\alpha$ полученное ранее для уравнения Ван дер Ваальса, это $${\frac {2a(v-b)^{2}-RTv^{2}b}{RTv^{3}-2a(v-b)^{2}}}=0\quad {\mbox{or}}\quad 2a(v-b)^{2}-RTv^{2}b=0$$Обратите внимание, что для $v\gg b$ будет охлаждение для $2a>RTb$ или через критическую температуру $T<27T_{\text{c}}/4$. Как заметил Зоммерфельд, «так обстоит дело с воздухом и большинством других газов. Воздух можно охлаждать по желанию путем многократного расширения и, наконец, сжижать » .

Рисунок 5: Кривые постоянной энтальпии в этой плоскости имеют отрицательный наклон над этой (зеленой) инверсионной кривой, положительный наклон под ней и нулевой наклон на ней; они S-образные. Газ, поступающий в дроссель в состоянии, соответствующем точке на этой кривой справа от ее максимума, будет охлаждаться, если конечное состояние находится ниже кривой. Другая кривая (пунктирная фиолетовая) на графике — это кривая насыщенности. График справа представляет собой квадрат (0,0),(1.1,1.1) левого графика, расширенный для отображения перекрытия кривых инверсии и насыщения.

Кривую инверсии можно найти, решив ее уравнение для $b/v$и подставляя в уравнение ВДВ. Это производит $p/p^{*}=-1+4(T/2T^{*})^{1/2}-3(T/2T^{*})$, где для простоты $a,b,R$ были заменены на $p^{*},T^{*}$.

Максимум этой квадратичной кривой имеет место при $z^{2}=T/(2T^{*})$, для $$D_{z}p/p^{*}=4-6(T/2T^{*})^{1/2}=0$$что дает $(T/2T^{*})_{\rm {max}}^{1/2}=2/3$, или $T_{\rm {max}}=8T^{*}/9$и соответствующий $p_{\rm {max}}=p^{*}/3$. Нули кривой инверсии $3z^{2}-4z+1=0$, являются, используя квадратичную формулу, $z=(4\pm {\sqrt {16-12}}\,)/6$, или $z=1/3$ и $1$ ( $T/T^{*}=2/9=0.{\overline {2}}$ и $2$). Что касается безразмерных переменных, $T_{r},p_{r}$ нули находятся на $T_{r}=3/4$ и $27/4$, а максимум $p_{r{\rm {max}}}=9$, и происходит при $T_{r{\rm {max}}}=3$. Обратите внимание на рис. 5, что кривая насыщения и кривая инверсии, построенная на ней, перекрываются. Эта область показана в увеличенном виде на правом графике рисунка. Следовательно, газ Ван-дер-Ваальса можно сжижать, пропуская его через дроссель при соответствующих условиях; настоящие газы сжижаются именно таким способом.

Коэффициент сжимаемости

Рисунок 6: Изотермы, спинодальные кривые и кривые сосуществования здесь такие же, как на рис. 1. Кроме того, изотерма $T_{r}=27/8$, который имеет нулевой наклон в начале координат, строится изотерма $T_{r}=\infty$. Абсцисса здесь $v^{*}\rho =\rho _{r}/3$ который варьируется от 0 до 1.

Рисунок 7: Обобщенная диаграмма сжимаемости газа Ван-дер-Ваальса.

Реальные газы можно охарактеризовать по их отличию от идеальных. Это делается путем записи механического уравнения состояния в виде $pv=ZRT$ где $Z$, называемый коэффициентом сжимаемости, обычно выражается либо как функция давления и температуры, либо как функция плотности и температуры, и в каждом случае в пределе $p$ или $\rho =1/v\rightarrow 0$, $Z=1$, идеальное значение газа.Во втором случае $p=Z(\rho ,T)\rho RT$. Таким образом, для жидкости Ван-дер-Ваальса коэффициент сжимаемости равен $Z=1/(1-b\rho )-a\rho /(RT)$, или в терминах приведенных переменных $$Z={\frac {3}{3-\rho _{r}}}-{\frac {9\rho _{r}}{8T_{r}}}$$где $0\leq \rho _{r}=1/v_{r}\leq 3$. В критической точке, $T_{r}=\rho _{r}=1$, $Z=Z_{\text{c}}=3/2-9/8=3/8$.

В пределе $\rho _{r}\rightarrow 0$, $Z=1$ (для конечного $T$); жидкость ведет себя как идеальный газ, и это отмечалось несколько раз ранее. Дополнительно отметим, что производная $D_{\rho _{r}}Z=3/(3-\rho _{r})^{2}-9/(8T_{r})=0$ для $T_{r}=3(3-\rho _{r})^{2}/8$, и когда $\rho _{r}=0$ Это $T_{r}=27/8$. Наклон может быть положительным или отрицательным в зависимости от того, $T_{r}$ больше или меньше $27/8$, и становится бесконечно большим отрицательным, поскольку $T$ подходы $0$.

На рис. 6 показаны графики различных изотерм $Z(\rho ,T_{r})$ против $\rho _{r}$. Также показаны спинодальные кривые и кривые сосуществования, описанные ранее. Докритическая изотерма состоит из стабильных, метастабильных и нестабильных сегментов и обозначена так же, как на рис. 1. Также включены изотерма с нулевым начальным наклоном и изотерма, соответствующая бесконечной температуре.

Построив график $Z(\rho _{r},T_{r})$ против $p_{r}(\rho _{r},T_{r})$ с использованием $\rho _{r}$ В качестве параметра получается обобщенная диаграмма сжимаемости газа ВДВ, которая представлена ​​на рис. 7. Как и все другие свойства ВДВ, она не является количественно правильной для большинства газов, но имеет правильные качественные характеристики, что видно из сравнения. с этой цифрой , которая была получена на основе данных с использованием реальных газов. Эти два графика похожи, включая каустику, созданную изотермами пересечения; качественно они очень похожи.

Вириальное расширение

Статистическая механика предполагает, что $Z$ может быть выражено степенным рядом, называемым вириальным разложением, $$Z(\rho ,T)=1+\sum _{k=1}^{\infty }\,V_{k}(T)(\rho )^{k}$$Функции $V_{k}(T)$ – вириальные коэффициенты; тот $k$этот термин представляет собой $k+1$ взаимодействие частиц.

Если заметить в выражении для $Z(\rho _{r},T_{r})$ это для $\rho _{r}<3$, термин $(3-\rho _{r})^{-1}$ можно разложить в абсолютно сходящийся ряд; это дает $$Z(\rho _{r},T_{r})=1+[1-27/(8T_{r})]^{-1}](\rho _{r}/3)+\sum _{k=2}^{\infty }\,(\rho _{r}/3)^{k}$$Это вириальное расширение жидкости Ван-дер-Ваальса. Первый вириальный коэффициент – это наклон $Z(\rho _{r},T_{r})$ в $\rho _{r}=0$. Обратите внимание, что оно может быть положительным или отрицательным в зависимости от того, $T_{r}>{\mbox{ or}}<27/8$, что согласуется с результатом, полученным ранее методом дифференцирования.

Для молекул, не притягивающих твердые сферы, $a=0$, вириальное расширение vdW становится просто $Z=(1-b\rho )^{-1}=\sum _{i=0}^{\infty }(b\rho )^{i}$, который иллюстрирует эффект только исключенного объема. Вначале было признано, что это ошибка, начиная с термина $(b\rho )^{2}$. Больцман рассчитал его правильное значение как $(5/8)(b\rho )^{2}$и использовал результат, чтобы предложить расширенную версию уравнения ВДВ $$(p+a/v^{2})(v-b/3)=RT[1+2b/(3v)+7b^{2}/(24v^{2})].$$О расширении $(v-b/3)^{-1}$, это дало правильные коэффициенты через $(b/v)^{2}$ а также давал бесконечное давление при $b/3$, что примерно соответствует расстоянию упаковки твердых сфер. Это было одно из первых из многих уравнений состояния, предложенных на протяжении многих лет, в которых была предпринята попытка количественного улучшения удивительно точного объяснения поведения реального газа, полученного с помощью уравнения ВДВ.

Смеси

В 1890 году Ван дер Ваальс опубликовал статью, положившую начало изучению смесей жидкостей. Впоследствии он был включен в Часть III позднее опубликованной версии его диссертации. Его основная идея заключалась в том, что в бинарной смеси ВДВ-жидкостей, описываемой уравнениями $$p_{1}={\frac {RT}{v-b_{11}}}-{\frac {a_{11}}{v^{2}}}\quad {\mbox{and}}\quad p_{2}={\frac {RT}{v-b_{22}}}-{\frac {a_{22}}{v^{2}}}$$смесь также представляет собой жидкость VdW, определяемую формулой $$p={\frac {RT}{v-b_{x}}}-{\frac {a_{x}}{v^{2}}}$$где $$a_{x}=a_{11}x_{1}^{2}+2a_{12}x_{1}x_{2}+a_{22}x_{2}^{2}\quad {\mbox{and}}\quad b_{x}=b_{11}x_{1}^{2}+2b_{12}x_{1}x_{2}+b_{22}x_{2}^{2}$$Здесь $x_{1}=N_{1}/N$, и $x_{2}=N_{2}/N$, с $N=N_{1}+N_{2}$ (так что $x_{1}+x_{2}=1$) — мольные доли двух жидких веществ. Сложение уравнений для двух жидкостей показывает, что $p\neq p_{1}+p_{2}$, хотя для $v$ достаточно большой $p\approx p_{1}+p_{2}$ при этом равенство сохраняется в пределе идеального газа. Квадратичные формы для $a_{x}$ и $b_{x}$ являются следствием сил между молекулами. Впервые это было показано Лоренцем. и был приписан ему Ван дер Ваальсом. Количества $a_{11},\,a_{22}$ и $b_{11},\,b_{22}$ в этих выражениях характеризуют столкновения двух молекул одного и того же компонента жидкости, а $a_{12}=a_{21}$ и $b_{12}=b_{21}$ представляют собой столкновения между одной молекулой каждой из двух различных составляющих жидкостей. Эту идею Ван дер Ваальса позже назвали одножидкостной моделью поведения смеси.

Предполагая, что $b_{12}$ это среднее арифметическое $b_{11}$ и $b_{22}$, $b_{12}=(b_{11}+b_{22})/2$, подставляя в квадратичную форму и отмечая, что $x_{1}+x_{2}=1$ производит $$b=b_{11}x_{1}+b_{22}x_{2}$$Ван дер Ваальс написал это соотношение, но изначально не использовал его. Однако он часто использовался в последующих исследованиях, и, как говорят, его использование дает хорошее согласие с экспериментальными результатами при высоком давлении.

В этой статье Ван дер Ваальс использовал принцип минимума потенциала Гельмгольца для установления условий устойчивости. Этот принцип гласит, что в системе, находящейся в диатермическом контакте с резервуаром тепла, $T=T_{R}$, $DF=0$ и $D^{2}F>0$, а именно в состоянии равновесия потенциал Гельмгольца является минимумом. Это приводит к требованию $\partial ^{2}f/\partial v^{2}|_{T}=-\partial p/\partial v|_{T}>0$, что является предыдущим условием устойчивости давления , но, кроме того, требует, чтобы функция $f=FN_{\mbox{A}}/N$, выпуклый вообще $v$ которые описывают устойчивые состояния.

Для одного вещества определение молярной свободной энергии Гиббса можно записать в виде $f=g-pv$. Таким образом, когда $p$ и $g$ постоянны вместе с температурой, функция $f(T_{R},v)$ представляет собой прямую линию с наклоном $-p$, и перехватить $g$. Поскольку кривая, $f(T_{R},v)$, имеет положительную кривизну всюду, когда $T_{R}\geq T_{c}$, кривая и прямая будут иметь одну касательную. Однако для докритического состояния $T_{R}$, с $p=p_{s}(T_{R})$ и подходящее значение $g$ линия будет касательной к $f(T_{R},v)$ при молярном объеме каждой сосуществующей фазы, насыщенной жидкости, $v_{f}(T_{R})$и насыщенный пар, $v_{g}(T_{R})$; будет двойная касательная. При этом каждая из этих точек характеризуется одинаковым значением $g$ а также те же значения $p$ и $T_{R}.$ Это те же три спецификации сосуществования, которые использовались ранее .

Рисунок 8: Прямая линия (сплошной пунктир черного цвета) касается кривой. $f_{r}(0.875,v_{r})$ (сплошной зеленый, пунктирный серый) в двух точках $v_{rf}=0.576$ и $v_{rg}=2.71$. Наклон прямой линии, определяемый выражением $\partial _{v_{r}}f_{r}=-p_{c}v_{c}/(RT_{c})p_{rs}$, является $-0.215$ соответствующий $p_{rs}=0.5730$. Все это согласуется с данными зеленой кривой, $T_{r}=7/8$, на рис. 1. Перехват на линии равен $g$, но его числовое значение произвольно из-за константы интегрирования.

Как показано на рис. 8, область на зеленой кривой $f(T_{R},v)$ для $v\leq v_{f}$ ( $v_{f}$ обозначен левым зеленым кружком) — жидкость. Как $v$ увеличивается в прошлом $v_{f}$ кривизна $f$ (пропорционально $\partial _{v^{2}}^{2}f=-\partial _{v}p$) постоянно уменьшается. Точка, характеризующаяся $\partial _{v^{2}}^{2}f=-\partial _{v}p=0$, является спинодальной точкой, а между этими двумя точками находится метастабильная перегретая жидкость. Для дальнейшего увеличения $v$ кривизна уменьшается до минимума, затем увеличивается до другой точки спинодали; между этими двумя точками спинодали находится неустойчивая область, в которой жидкость не может существовать в однородном равновесном состоянии. При дальнейшем увеличении $v$ кривизна увеличивается до максимума при $v_{g}$, где наклон $p_{s}$; область между этой точкой и второй точкой спинодали представляет собой метастабильный переохлажденный пар. Наконец, регион $v\geq v_{g}$ это пар. В этой области кривизна постоянно уменьшается, пока не станет равна нулю при бесконечно больших $v$. Двойная касательная линия между значениями насыщенной жидкости и пара отображается сплошной, чтобы указать, что состояния на ней стабильны, в отличие от метастабильных и нестабильных состояний над ней (с большей свободной энергией Гельмгольца), но черной, а не зеленой, чтобы указать что эти состояния являются гетерогенными, а не однородными решениями уравнения ВДВ.

Для жидкости ВДВ молярный потенциал Гельмгольца просто $$f_{r}=u_{r}-T_{r}s_{r}={\mbox{C}}_{u}+T_{r}\{c-{\mbox{C}}_{s}-\ln[T_{r}^{c}(3v_{r}-1)]\}-9/(8v_{r})$$где $f_{r}=f/(RT_{c})$. График этой функции для солнечнокритической изотермы $T_{r}=7/8$ — это та, которая показана на рис. 8 вместе с касательной к ней линией в двух сосуществующих точках насыщения. Данные, представленные на рис. 8, точно такие же, как и представленные на рис. 1 для этой изотермы.

Ван дер Ваальс ввел функцию Гельмгольца, потому что ее свойства можно было легко распространить на ситуацию с бинарной жидкостью. В бинарной смеси жидкостей ВДВ потенциал Гельмгольца является функцией двух переменных: $f(T_{R},v,x)$, где $x$ является композиционной переменной, например $x=x_{2}$ так $x_{1}=1-x$. В этом случае имеются три условия устойчивости $${\frac {\partial ^{2}f}{\partial v^{2}}}>0\qquad {\frac {\partial ^{2}f}{\partial x^{2}}}>0\qquad {\frac {\partial ^{2}f}{\partial v^{2}}}{\frac {\partial ^{2}f}{\partial x^{2}}}-\left({\frac {\partial ^{2}f}{\partial x\partial v}}\right)^{2}>0$$а потенциал Гельмгольца представляет собой поверхность (представляющую физический интерес в области $0\leq x\leq 1$). Первые два условия устойчивости показывают, что кривизна в каждом из направлений $v$ и $x$ оба положительны для стабильных состояний, а третье условие указывает, что стабильные состояния соответствуют эллиптическим точкам на этой поверхности. Более того, его предел, $\partial _{x^{2}}^{2}f\partial _{v^{2}}^{2}f-(\partial _{xv}^{2}f)^{2}=0$, в данном случае является спецификацией спинодальных точек.

Для бинарной смеси Эйлера уравнение можно записать в форме $$f=-pv+\mu _{1}x_{1}+\mu _{2}x_{2}=-pv+(\mu _{2}-\mu _{1})x+\mu _{1}$$Здесь $\mu _{j}=\partial _{x_{j}}f$ - молярные химические потенциалы каждого вещества, $j=1,2$. Для $p$, $\mu _{1}$ и $\mu _{2}$, все константы это уравнение плоскости с наклонами $-p$ в $v$ направление, $\mu _{2}-\mu _{1}$ в $x$ направление и перехватить $\mu _{1}$. Как и в случае с одним веществом, здесь плоскость и поверхность могут иметь двойную касательную, а геометрическое место сосуществующих фазовых точек образует кривую на каждой поверхности. Условия сосуществования заключаются в том, что две фазы имеют одинаковую $T$, $p$, $\mu _{2}-\mu _{1}$, и $\mu _{1}$; последние два эквивалентны наличию одного и того же $\mu _{1}$ и $\mu _{2}$ индивидуально, что и есть условия Гиббса для материального равновесия в этой ситуации. Хотя этот случай аналогичен предыдущему случаю с одним компонентом, здесь геометрия может быть намного сложнее. На поверхности может образовываться волна ( называемая жгутом или складкой) в в литературе $x$ направлении, а также в $v$ направление. Следовательно, могут существовать две жидкие фазы, которые могут быть либо смешивающимися, либо полностью или частично несмешивающимися, а также паровая фаза. Несмотря на большой объем как теоретических, так и экспериментальных работ по этой проблеме Ван дер Ваальса и его последователей, работы, которые дали много полезных знаний о различных типах фазового равновесия, возможных в смесях жидкостей, Полные решения проблемы были получены только после 1967 года, когда наличие современных компьютеров впервые сделало возможными расчеты математических задач такой сложности. Полученные результаты, по словам Роулинсона, были:

впечатляющее подтверждение существенной физической правильности идей, лежащих в основе уравнения Ван-дер-Ваальса, поскольку почти каждый вид критического поведения, обнаруженный на практике, может быть воспроизведен расчетами, а диапазон параметров, которые коррелируют с различными видами поведения, понятен с точки зрения ожидаемых эффектов размера и энергии.

Для получения таких численных результатов значения констант отдельных компонентов жидкостей $a_{11},a_{22},b_{11},b_{22}$ должно быть известно. Кроме того, эффект столкновений между молекулами разных компонентов, определяемый формулой $a_{12}$ и $b_{12}$, также необходимо указать. В отсутствие экспериментальных данных или результатов компьютерного моделирования для оценки их ценности эмпирические законы объединения $$a_{12}=(a_{11}a_{22})^{1/2}\qquad {\mbox{and}}\qquad b_{12}^{1/3}=(b_{11}^{1/3}+b_{22}^{1/3})/2,$$могут быть использованы соответственно геометрические и алгебраические средние. Эти соотношения соответствуют эмпирическим законам объединения межмолекулярных силовых констант: $$\epsilon _{12}=(\epsilon _{11}\epsilon _{22})^{1/2}\qquad {\mbox{and}}\qquad \sigma _{12}=(\sigma _{11}+\sigma _{22})/2,$$первый из которых следует из простой интерпретации дисперсионных сил через поляризуемость отдельных молекул, а второй является точным для жестких молекул. Тогда, обобщая $n$ жидкие компоненты, и используя эти эмпирические законы комбинирования, выражения для материальных констант имеют вид: $$a_{x}=\sum _{i=1}^{n}\sum _{j=1}^{n}(a_{ii}a_{jj})^{1/2}x_{i}x_{j}\quad {\mbox{which can be written as}}\quad a_{x}={\Big (}\sum _{i=1}^{n}a_{ii}^{1/2}x_{i}{\Big )}^{2}$$$$b_{x}=(1/8)\sum _{i=1}^{n}\sum _{j=1}^{n}(b_{ii}^{1/3}+b_{jj}^{1/3})^{3}x_{i}x_{j}$$Использование этих выражений в уравнении ВДВ, очевидно, полезно для дайверов. а также важно для физиков, физико-химиков и инженеров-химиков в их изучении и управлении различными фазовыми равновесиями и критическим поведением, наблюдаемыми в смесях жидкостей.

Другой метод задания констант vdW, впервые предложенный У.Б. Кеем и известный как правило Кея. определяет эффективную критическую температуру и давление смеси жидкостей по формуле $$T_{cx}=\sum _{i=1}^{n}T_{ci}x_{i}\qquad {\mbox{and}}\qquad p_{cx}=\sum _{i=1}^{n}\,p_{ci}x_{i}$$Тогда, выражая эти величины, константы смеси ВДВ будут равны: $$a_{x}={\frac {27}{64}}{\frac {(RT_{cx})^{2}}{p_{cx}}}\qquad \qquad b_{x}={\frac {1}{8}}{\frac {RT_{cx}}{p_{cx}}}$$и Кей использовали эти характеристики критических констант смеси как основу для расчетов термодинамических свойств смесей.

Идея Кея была принята Т.В. Леландом, который применил ее к молекулярным параметрам. $\epsilon ,\sigma$, которые связаны с $a,b$ через $T_{c},p_{c}$ к $a\propto \epsilon \sigma ^{3}$ и $b\propto \sigma ^{3}$ (см. введение к этой статье ). Используя их вместе с квадратичной формой $a,b$ для смесей производит $$\sigma _{x}^{3}=\sum _{i=i}^{n}\sum _{j=1}^{n}\,\sigma _{ij}^{3}x_{i}x_{j}\qquad {\mbox{and}}\qquad \epsilon _{x}=\left[\sum _{i=1}^{n}\sum _{j=1}^{n}\epsilon _{ij}\sigma _{ij}^{3}x_{i}x_{j}\right]\left[\sum _{i=i}^{n}\sum _{j=1}^{n}\,\sigma _{ij}^{3}x_{i}x_{j}\right]^{-1}$$ что представляет собой приближение Ван-дер-Ваальса, выраженное через межмолекулярные константы. Это приближение по сравнению с компьютерным моделированием смесей хорошо согласуется в диапазоне $1/2<(\sigma _{11}/\sigma _{22})^{3}<2$, а именно для молекул не слишком разных диаметров. Фактически Роулинсон сказал об этом приближении: «Было и до сих пор трудно улучшить первоначальный рецепт Ван дер Ваальса, когда он выражен в [этой] форме».

Вывод

В учебниках по физической химии обычно приводятся два вывода заглавного уравнения. Один из них — традиционный вывод, восходящий к Ван-дер-Ваальсу, механическому уравнению состояния, которое нельзя использовать для описания всех термодинамических функций; другой представляет собой вывод статистической механики, который делает явным межмолекулярный потенциал, которым пренебрегали в первом выводе. Особым преимуществом статистического механического вывода является то, что он дает статистическую сумму системы и позволяет указать все термодинамические функции (включая механическое уравнение состояния).

Традиционный вывод

Рассмотрим один моль газа, состоящий из невзаимодействующих точечных частиц, удовлетворяющих закону идеального газа: (см. любой стандартный учебник по физической химии, указ. соч.)

$p={\frac {RT}{V_{\mathrm {m} }}}.$

Далее предположим, что все частицы представляют собой твердые сферы одного и того же конечного радиуса r ( радиус Ван-дер-Ваальса ). Эффект конечного объема частиц заключается в уменьшении доступного пустого пространства, в котором частицы могут свободно перемещаться. Мы должны заменить V на V − b , где b называется исключенным объемом (на моль) или «совместным объемом». Исправленное уравнение становится

$p={\frac {RT}{V_{\mathrm {m} }-b}}.$

Исключенный объем $b$ не просто равен объему, занимаемому твердыми частицами конечного размера, но фактически в четыре раза превышает общий молекулярный объем одного моля газа Ван-дер-Ваальса. Чтобы увидеть это, мы должны осознать, что частица окружена сферой радиуса 2 r (в два раза превышающей первоначальный радиус), которая запрещена для центров других частиц. Если бы расстояние между центрами двух частиц было меньше 2 r , это означало бы, что две частицы проникают друг в друга, чего по определению твердые сферы сделать не могут.

Исключенный объем для двух частиц (среднего диаметра d или радиуса r ) равен

$b'_{2}=4\pi d^{3}/3=8\times (4\pi r^{3}/3)$,

которое, разделенное на два (количество сталкивающихся частиц), дает исключенный объем на одну частицу:

$b'=b'_{2}/2\quad \rightarrow \quad b'=4\times (4\pi r^{3}/3)$,

Таким образом, b ' в четыре раза превышает собственный объем частицы. Ван дер Ваальса беспокоило то, что коэффициент четыре дает верхнюю границу; эмпирические значения b ' обычно ниже. Конечно, молекулы не являются бесконечно твердыми, как считал Ван дер Ваальс, и часто бывают довольно мягкими. Чтобы получить исключенный объем на моль, нам просто нужно умножить его на количество молекул в моле, т. е. на число Авогадро:

$b=N_{\text{A}}b'$.

Далее мы вводим (не обязательно парную) силу притяжения между частицами. Ван дер Ваальс предполагал, что, несмотря на существование этой силы, плотность жидкости однородна; более того, он предположил, что диапазон действия силы притяжения настолько мал, что подавляющее большинство частиц не чувствуют, что контейнер имеет конечный размер. Учитывая однородность жидкости, основная масса частиц не испытывает результирующей силы, тянущей их вправо или влево. Иначе обстоит дело с частицами в поверхностных слоях, непосредственно прилегающих к стенкам. Они чувствуют результирующую силу от объемных частиц, втягивающую их в контейнер, поскольку эта сила не компенсируется частицами на той стороне, где находится стенка (здесь еще одно предположение состоит в том, что между стенками и частицами нет взаимодействия, что неверно, как видно по явлению образования капель, большинство типов жидкостей обладают адгезией). Эта результирующая сила уменьшает силу, действующую на стенку со стороны частиц в поверхностном слое. Суммарная сила, действующая на поверхностную частицу, втягивающая ее в контейнер, пропорциональна плотности чисел. Если рассматривать один моль газа, число частиц будет N _A

$C=N_{\mathrm {A} }/V_{\mathrm {m} }$.

Число частиц в поверхностных слоях, опять же в предположении однородности, также пропорционально плотности. В сумме сила, действующая на стенки, уменьшается в раз, пропорциональный квадрату плотности, а давление (сила на единицу поверхности) уменьшается в:

$a'C^{2}=a'\left({\frac {N_{\mathrm {A} }}{V_{\mathrm {m} }}}\right)^{2}={\frac {a}{V_{\mathrm {m} }^{2}}}$,

так что:

$p={\frac {RT}{V_{\mathrm {m} }-b}}-{\frac {a}{V_{\mathrm {m} }^{2}}}\Rightarrow \left(p+{\frac {a}{V_{\mathrm {m} }^{2}}}\right)(V_{\mathrm {m} }-b)=RT.$

Если записать n для числа молей и nV _m = V , уравнение примет вторую форму, приведенную выше:

$\left(p+{\frac {n^{2}a}{V^{2}}}\right)(V-nb)=nRT.$

Представляет некоторый исторический интерес отметить, что Ван дер Ваальс в своей лекции, присужденной Нобелевской премии, отдал должное Лапласу за аргумент о том, что давление уменьшается пропорционально квадрату плотности.

термодинамики

Каноническая статистическая сумма Z идеального газа, состоящего из N = nN _A одинаковых ( невзаимодействующих ) частиц, равна:

$Z={\frac {z^{N}}{N!}}\quad {\hbox{with}}\quad z={\frac {V}{\Lambda ^{3}}}$

где $\Lambda$ — тепловая длина волны де Бройля :

$\Lambda ={\sqrt {\frac {h^{2}}{2\pi mkT}}}$

с обычными определениями: h — постоянная Планка , m — масса частицы, k — и постоянная Больцмана T — абсолютная температура. В идеальном газе z статистическая сумма отдельной частицы в сосуде объёмом V. — Чтобы вывести уравнение Ван-дер-Ваальса, мы предполагаем теперь, что каждая частица движется независимо в среднем потенциальном поле, создаваемом другими частицами. Усреднение по частицам несложно, поскольку мы будем предполагать, что плотность частиц жидкости Ван-дер-Ваальса однородна.Взаимодействие между парой частиц, представляющих собой твердые сферы, принимается равным:

$u(r)={\begin{cases}\infty &{\hbox{when}}\quad r<d,\\-\epsilon \left({\frac {d}{r}}\right)^{6}&{\hbox{when}}\quad r\geq d,\end{cases}}$

r — расстояние между центрами сфер, а d — расстояние, на котором твердые сферы касаются друг друга (дважды радиус Ван-дер-Ваальса). Глубина скважины Ван-дер-Ваальса составляет $\epsilon$.

Поскольку частицы не связаны гамильтонианом среднего поля, приближение среднего поля полной статистической суммы по-прежнему факторизуется:

$Z=z^{N}/N!$,

но межмолекулярный потенциал требует двух модификаций z . Во-первых, из-за конечного размера частиц не весь V доступен , а только V − Nb ′, где (так же, как и в обычном выводе выше):

$b'=2\pi d^{3}/3$.

Во-вторых, мы вставляем фактор Больцмана exp[−Φ/2 kT ] для учета среднего межмолекулярного потенциала. Мы делим здесь потенциал на два, потому что эта энергия взаимодействия распределяется между двумя частицами. Таким образом:

$z={\frac {(V-Nb')\,e^{-\phi /(2kT)}}{\Lambda ^{3}}}.$

Полное притяжение, ощущаемое отдельной частицей, равно:

$\phi =\int _{d}^{\infty }u(r){\frac {N}{V}}4\pi r^{2}dr,$

где мы предполагали, что в оболочке толщиной d r имеются N / V 4 π r ² доктор частиц. Это приближение среднего поля; положение частиц усредняется. В действительности плотность вблизи частицы отличается от плотности вдали, что можно описать парной корреляционной функцией. При этом не учитывается, что жидкость заключена между стенками. Выполнив интеграл, получим:

$\phi =-2a'{\frac {N}{V}}\quad {\hbox{with}}\quad a'=\epsilon {\frac {2\pi d^{3}}{3}}=\epsilon b'.$

Следовательно, мы получаем:

$\ln Z=N\ln {(V-Nb')}+{\frac {N^{2}a'}{VkT}}-N\ln {(\Lambda ^{3})}-\ln {N!}$

Из статистической термодинамики мы знаем, что:

$p=kT{\frac {\partial \ln Z}{\partial V}}$,

так что нам остается только дифференцировать термины, содержащие $V$. Мы получаем:

$p={\frac {NkT}{V-Nb'}}-{\frac {N^{2}a'}{V^{2}}}\Rightarrow \left(p+{\frac {N^{2}a'}{V^{2}}}\right)(V-Nb')=NkT\Rightarrow \left(p+{\frac {n^{2}a}{V^{2}}}\right)(V-nb)=nRT.$

См. также

• Газовые законы
• Идеальный газ
• Температура инверсии
• Итерация
• Конструкция Максвелла
• настоящий газ
• Теорема о соответствующих состояниях
• Константы Ван-дер-Ваальса (страница данных)
• Уравнение состояния Редлиха – Квонга

Дальнейшее чтение

• Чендлер, Дэвид (1987). Введение в современную статистическую механику . Оксфорд: Издательство Оксфордского университета. стр. 287–295. ISBN  0195042778 .
• Кросс, Майкл (2004), «Лекция 3: Фазовые переходы первого рода» (PDF) , Физика 127: Статистическая физика, второй семестр , Пасадена, Калифорния: Отдел физики, математики и астрономии, Калифорнийский технологический институт .
• Далгарно, А.; Дэвисон, У.Д. (1966). «Расчет Ван-дер-Ваальсовых взаимодействий». Достижения атомной и молекулярной физики . 2 : 1–32. Бибкод : 1966AdAMP...2....1D . дои : 10.1016/S0065-2199(08)60216-X . ISBN  9780120038022 .
• Киттель, Чарльз; Кремер, Герберт (1980). Теплофизика (пересмотренная ред.). Нью-Йорк: Макмиллан. стр. 287–295. ISBN  0716710889 .