Распределение Больцмана

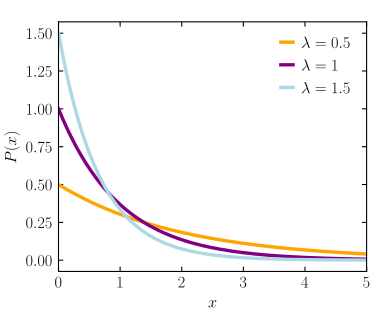
В статистической механике и математике распределение Больцмана (также называемое распределением Гиббса) ^{[ 1 ]}) — это распределение вероятностей или вероятностная мера , которая дает вероятность того, что система будет находиться в определенном состоянии , как функцию энергии этого состояния и температуры системы. Распределение выражается в виде:

p_{i}\propto \exp \left(-{\frac {\varepsilon _{i}}{kT}}\right)

где $p i$ — вероятность того, что система находится в состоянии $i$ , $exp$ — экспоненциальная функция , $ε i$ энергия этого состояния, а константа $kT$ распределения — это произведение константы Больцмана $k$ и термодинамической температуры $T.$ — Символ ${\textstyle \propto }$ обозначает пропорциональность (см . § Распределение константы пропорциональности).

Термин «система» здесь имеет широкое значение; он может варьироваться от набора «достаточного количества» атомов или одного атома. ^{[ 1 ]} в макроскопическую систему, такую как резервуар для хранения природного газа . Поэтому распределение Больцмана можно использовать для решения широкого круга задач. Распределение показывает, что состояния с более низкой энергией всегда будут иметь более высокую вероятность быть занятыми.

Отношение вероятностей двух состояний известно как фактор Больцмана и, как правило, зависит только от разности энергий состояний:

{\frac {p_{i}}{p_{j}}}=\exp \left({\frac {\varepsilon _{j}-\varepsilon _{i}}{kT}}\right)

Распределение Больцмана названо в честь Людвига Больцмана, который впервые сформулировал его в 1868 году во время исследований статистической механики газов, находящихся в тепловом равновесии . ^{[ 2 ]} Статистическая работа Больцмана подтверждается его статьей «О связи между второй основной теоремой механической теории теплоты и вероятностными расчетами условий теплового равновесия». ^{[ 3 ]} Позже это распределение в его современной общей форме было тщательно исследовано Джозайей Уиллардом Гиббсом в 1902 году. ^{[ 4 ]}

Распределение Больцмана не следует путать с распределением Максвелла-Больцмана или статистикой Максвелла-Больцмана . Распределение Больцмана дает вероятность того, что система будет находиться в определенном состоянии , как функцию энергии этого состояния. ^{[ 5 ]} в то время как распределения Максвелла-Больцмана дают вероятности скоростей или энергий частиц в идеальных газах. Однако распределение энергий в одномерном газе действительно соответствует распределению Больцмана.

Распределение

Распределение Больцмана — это распределение вероятностей , которое дает вероятность определенного состояния как функцию энергии этого состояния и температуры системы, к которой применяется это распределение. ^{[ 6 ]} Это дано как $p_{i}={\frac {1}{Q}}\exp \left(-{\frac {\varepsilon _{i}}{kT}}\right)={\frac {\exp \left(-{\tfrac {\varepsilon _{i}}{kT}}\right)}{\displaystyle \sum _{j=1}^{M}\exp \left(-{\tfrac {\varepsilon _{j}}{kT}}\right)}}$

где:

$exp()$ — показательная функция ,
$p i$ — вероятность состояния $i$ ,
$ε i$ — энергия состояния $i$ ,
$k$ — постоянная Больцмана ,
$T$ – абсолютная температура системы,
$M$ — количество всех состояний, доступных интересующей системе, ^{[ 6 ]}^{[ 5 ]}
$Q$ (обозначаемый некоторыми авторами $Z$ ) — знаменатель нормализации, который является канонической статистической суммой $Q=\sum _{j=1}^{M}\exp \left(-{\tfrac {\varepsilon _{j}}{kT}}\right)$ Это происходит из-за ограничения, согласно которому суммы вероятностей всех доступных состояний должны составлять 1.

Используя множители Лагранжа , можно доказать, что распределение Больцмана — это распределение, которое максимизирует энтропию. $S(p_{1},p_{2},\cdots ,p_{M})=-\sum _{i=1}^{M}p_{i}\log _{2}p_{i}$

при условии ограничения нормализации, которое ${\textstyle \sum p_{i}=1}$ и ограничение, которое ${\textstyle \sum {p_{i}{\varepsilon }_{i}}}$ равно определенному значению средней энергии, за исключением двух особых случаев. (Эти особые случаи возникают, когда среднее значение является минимумом или максимумом энергий $ε i$ . В этих случаях распределение, максимизирующее энтропию, является пределом распределений Больцмана, где $T$ приближается к нулю сверху или снизу соответственно.)

Статистическая сумма может быть вычислена, если мы знаем энергии состояний, доступных интересующей системе. Значения статистической суммы для атомов можно найти в базе данных атомных спектров NIST . ^{[ 7 ]}

Распределение показывает, что состояния с более низкой энергией всегда будут иметь более высокую вероятность быть занятыми, чем состояния с более высокой энергией. Это также может дать нам количественную связь между вероятностями оккупации двух состояний. Отношение вероятностей состояний $i$ и $j$ определяется как ${\frac {p_{i}}{p_{j}}}=\exp \left({\frac {\varepsilon _{j}-\varepsilon _{i}}{kT}}\right)$

где:

$p i$ — вероятность состояния $i$ ,
$p j$ вероятность состояния $j$ ,
$ε i$ — энергия состояния $i$ ,
$ε j$ — энергия состояния $j$ .

Соответствующее соотношение населенностей энергетических уровней должно учитывать и их . вырождения

Распределение Больцмана часто используется для описания распределения частиц, таких как атомы или молекулы, по доступным им связанным состояниям. Если у нас есть система, состоящая из множества частиц, вероятность того, что частица находится в состоянии $i$ , практически равна вероятности того, что, если мы выберем случайную частицу из этой системы и проверим, в каком состоянии она находится, мы обнаружим, что она находится в состоянии $i.$ . Эта вероятность равна числу частиц в состоянии $i,$ делённому на общее количество частиц в системе, то есть долю частиц, занимающих состояние $i$ .

p_{i}={\frac {N_{i}}{N}}

где $N i$ — количество частиц в состоянии $i$ , а $N$ — общее количество частиц в системе. Мы можем использовать распределение Больцмана, чтобы найти эту вероятность, которая, как мы видели, равна доле частиц, находящихся в состоянии i. Таким образом, уравнение, которое дает долю частиц в состоянии $i$ как функцию энергии этого состояния, имеет вид ^{[ 5 ]} ${\frac {N_{i}}{N}}={\frac {\exp \left(-{\frac {\varepsilon _{i}}{kT}}\right)}{\displaystyle \sum _{j=1}^{M}\exp \left(-{\tfrac {\varepsilon _{j}}{kT}}\right)}}$

Это уравнение имеет большое значение для спектроскопии . В спектроскопии мы наблюдаем спектральную линию атомов или молекул, претерпевающих переходы из одного состояния в другое. ^{[ 5 ]}^{[ 8 ]} Для того чтобы это было возможно, в первом состоянии должны находиться некоторые частицы, которые претерпят переход. Мы можем обнаружить, что это условие выполняется, найдя долю частиц в первом состоянии. Если она пренебрежимо мала, то переход, скорее всего, не наблюдается при температуре, для которой проводился расчет. В общем, большая доля молекул в первом состоянии означает большее количество переходов во второе состояние. ^{[ 9 ]} Это дает более сильную спектральную линию. Однако существуют и другие факторы, влияющие на интенсивность спектральной линии, например, вызвана ли она разрешенным или запрещенным переходом .

Функция softmax, обычно используемая в машинном обучении, связана с распределением Больцмана:

(p_{1},\ldots ,p_{M})=\operatorname {softmax} \left[-{\frac {\varepsilon _{1}}{kT}},\ldots ,-{\frac {\varepsilon _{M}}{kT}}\right]

Обобщенное распределение Больцмана

Распространение формы

\Pr \left(\omega \right)\propto \exp \left[\sum _{\eta =1}^{n}{\frac {X_{\eta }x_{\eta }^{\left(\omega \right)}}{k_{B}T}}-{\frac {E^{\left(\omega \right)}}{k_{B}T}}\right]

называют обобщенным распределением Больцмана . некоторые авторы ^{[ 10 ]}

Распределение Больцмана является частным случаем обобщенного распределения Больцмана. Обобщенное распределение Больцмана используется в статистической механике для описания канонического ансамбля , большого канонического ансамбля и изотермически-изобарического ансамбля . Обобщенное распределение Больцмана обычно выводится из принципа максимальной энтропии , но существуют и другие выводы. ^{[ 10 ]}^{[ 11 ]}

Обобщенное распределение Больцмана обладает следующими свойствами:

Это единственное распределение, для которого энтропия, определенная формулой энтропии Гиббса, совпадает с энтропией, определенной в классической термодинамике . ^{[ 10 ]}
Это единственное распределение, которое математически согласуется с фундаментальным термодинамическим соотношением , в котором функции состояния описываются средним по ансамблю. ^{[ 11 ]}

В статистической механике

Распределение Больцмана появляется в статистической механике при рассмотрении замкнутых систем фиксированного состава, находящихся в тепловом равновесии (равновесии по отношению к обмену энергией). Наиболее общим случаем является распределение вероятностей канонического ансамбля. Некоторые частные случаи (вытекающие из канонического ансамбля) демонстрируют распределение Больцмана в разных аспектах:

Канонический ансамбль (общий случай): Канонический ансамбль дает вероятности различных возможных состояний замкнутой системы фиксированного объема, находящейся в тепловом равновесии с тепловой баней . Канонический ансамбль имеет распределение вероятностей состояний с формой Больцмана.
Статистические частоты состояний подсистем (в невзаимодействующей совокупности): Когда интересующая система представляет собой набор множества невзаимодействующих копий меньшей подсистемы, иногда полезно найти статистическую частоту данного состояния подсистемы среди этой коллекции. Канонический ансамбль обладает свойством отделимости применительно к такой совокупности: пока невзаимодействующие подсистемы имеют фиксированный состав, то состояние каждой подсистемы независимо от других и также характеризуется каноническим ансамблем. В результате ожидаемое статистическое распределение частот состояний подсистемы имеет больцмановскую форму.
Статистика Максвелла – Больцмана классических газов (систем невзаимодействующих частиц): В системах частиц многие частицы делят одно и то же пространство и регулярно меняются местами друг с другом; пространство одночастичных состояний, которое они занимают, является общим пространством. Статистика Максвелла – Больцмана дает ожидаемое количество частиц, находящихся в данном одночастичном состоянии, в классическом газе невзаимодействующих частиц, находящихся в равновесии. Это ожидаемое распределение чисел имеет форму Больцмана.

Хотя эти случаи имеют большое сходство, полезно различать их, поскольку они по-разному обобщаются при изменении важнейших предположений:

Когда система находится в термодинамическом равновесии как в отношении обмена энергией, так и в отношении обмена частицами , требование фиксированного состава ослабляется и большой канонический ансамбль получается , а не канонический ансамбль. С другой стороны, если и состав, и энергия фиксированы, то вместо этого применяется микроканонический ансамбль .
Если подсистемы внутри набора взаимодействуют друг с другом, то ожидаемые частоты состояний подсистем больше не подчиняются распределению Больцмана и даже могут не иметь аналитического решения . ^{[ 12 ]} Однако канонический ансамбль все еще можно применять к коллективным состояниям всей системы, рассматриваемой как единое целое, при условии, что вся система находится в тепловом равновесии.
Когда квантовые газы невзаимодействующих частиц находятся в равновесии, количество частиц, находящихся в данном одночастичном состоянии, не соответствует статистике Максвелла – Больцмана, и не существует простого выражения в замкнутой форме для квантовых газов в каноническом ансамбле. В большом каноническом ансамбле статистика заполнения состояний квантовых газов описывается статистикой Ферми-Дирака или статистикой Бозе-Эйнштейна , в зависимости от того, являются ли частицы фермионами или бозонами соответственно.

По математике

В более общих математических терминах распределение Больцмана также известно как мера Гиббса .
В статистике и машинном обучении это называется лог-линейной моделью .
В глубоком обучении распределение Больцмана используется при распределении выборки стохастических нейронных сетей, таких как машина Больцмана , ограниченная машина Больцмана , модели на основе энергии и глубокая машина Больцмана . В глубоком обучении машина Больцмана считается одной из моделей обучения без учителя . При разработке машины Больцмана для глубокого обучения по мере увеличения количества узлов сложность реализации приложений реального времени становится критической, поэтому другой тип архитектуры, называемый ограниченной машиной Больцмана . вводится

В экономике

Распределение Больцмана может быть введено для распределения разрешений при торговле выбросами . ^{[ 13 ]}^{[ 14 ]} Новый метод распределения с использованием распределения Больцмана может описать наиболее вероятное, естественное и объективное распределение разрешений на выбросы между несколькими странами.

Распределение Больцмана имеет ту же форму, что и полиномиальная логит- модель. Как модель дискретного выбора , она очень хорошо известна в экономике с тех пор, как Дэниел Макфадден связал ее с максимизацией случайной полезности. ^{[ 15 ]}

См. также

Ссылки

^ Jump up to: ^а ^б Ландау, Лев Давидович и Лифшиц, Евгений Михайлович (1980) [1976]. Статистическая физика . Курс теоретической физики. Том. 5 (3-е изд.). Оксфорд: Пергамон Пресс. ISBN 0-7506-3372-7 . Перевод Дж. Б. Сайкса и М. Дж. Кирсли. См. раздел 28.
^ Больцман, Людвиг (1868). «Исследования баланса жизненной силы между движущимися материальными точками». Об этом сообщает Вена . 58 :517-560.
^ «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 05 марта 2021 г. Проверено 11 мая 2017 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )
^ Гиббс, Джозайя Уиллард (1902). Элементарные начала статистической механики . Нью-Йорк: Сыновья Чарльза Скрибнера .
^ Jump up to: ^а ^б ^с ^д Аткинс, PW (2010) Quanta, WH Freeman and Company, Нью-Йорк
^ Jump up to: ^а ^б МакКуорри, А. (2000). Статистическая механика . Саусалито, Калифорния: Университетские научные книги. ISBN 1-891389-15-7 .
^ Форма уровней базы данных атомных спектров NIST на nist.gov
^ Аткинс, П.В.; де Паула, Дж. (2009). Физическая химия (9-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-954337-3 .
^ Скуг, Д.А.; Холлер, Ф.Дж.; Крауч, СР (2006). Принципы инструментального анализа . Бостон, Массачусетс: Брукс/Коул. ISBN 978-0-495-12570-9 .
^ Jump up to: ^а ^б ^с Гао, Сян; Галликкио, Эмилио; Ройтберг, Адриан (2019). «Обобщенное распределение Больцмана — единственное распределение, в котором энтропия Гиббса-Шеннона равна термодинамической энтропии» . Журнал химической физики . 151 (3): 034113. arXiv : 1903.02121 . Бибкод : 2019JChPh.151c4113G . дои : 10.1063/1.5111333 . ПМИД 31325924 . S2CID 118981017 .
^ Jump up to: ^а ^б Гао, Сян (март 2022 г.). «Математика теории ансамбля» . Результаты по физике . 34 : 105230. arXiv : 2006.00485 . Бибкод : 2022ResPh..3405230G . дои : 10.1016/j.rinp.2022.105230 . S2CID 221978379 .
^ Классический пример этого — магнитное упорядочение . Системы невзаимодействующих спинов демонстрируют парамагнитное поведение, которое можно понять с помощью одночастичного канонического ансамбля (что приводит к функции Бриллюэна ). Системы взаимодействующих спинов могут демонстрировать гораздо более сложное поведение, такое как ферромагнетизм или антиферромагнетизм .
^ Парк, Дж.-В., Ким, К.У. и Айсард, В. (2012) Распределение разрешений на торговлю выбросами с использованием распределения Больцмана. Физика А 391: 4883–4890.
^ Сложная проблема справедливого распределения . Блог Technology Review . 17 августа 2011 г. Цитирует и резюмирует Пак, Ким и Айсард (2012).
^ Амемия, Такеши (1985). «Мультиномиальная логит-модель» . Продвинутая эконометрика . Оксфорд: Бэзил Блэквелл. стр. 295–299. ISBN 0-631-13345-3 .

[landau-1] Jump up to: ^а ^б Ландау, Лев Давидович и Лифшиц, Евгений Михайлович (1980) [1976]. Статистическая физика . Курс теоретической физики. Том. 5 (3-е изд.). Оксфорд: Пергамон Пресс. ISBN 0-7506-3372-7 . Перевод Дж. Б. Сайкса и М. Дж. Кирсли. См. раздел 28.

[2] Больцман, Людвиг (1868). «Исследования баланса жизненной силы между движущимися материальными точками». Об этом сообщает Вена . 58 :517-560.

[3] «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 05 марта 2021 г. Проверено 11 мая 2017 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )

[gibbs-4] Гиббс, Джозайя Уиллард (1902). Элементарные начала статистической механики . Нью-Йорк: Сыновья Чарльза Скрибнера .

[Atkins,_P._W._2010-5] Jump up to: ^а ^б ^с ^д Аткинс, PW (2010) Quanta, WH Freeman and Company, Нью-Йорк

[McQuarrie,_A._2000-6] Jump up to: ^а ^б МакКуорри, А. (2000). Статистическая механика . Саусалито, Калифорния: Университетские научные книги. ISBN 1-891389-15-7 .

[7] Форма уровней базы данных атомных спектров NIST на nist.gov

[8] Аткинс, П.В.; де Паула, Дж. (2009). Физическая химия (9-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-954337-3 .

[9] Скуг, Д.А.; Холлер, Ф.Дж.; Крауч, СР (2006). Принципы инструментального анализа . Бостон, Массачусетс: Брукс/Коул. ISBN 978-0-495-12570-9 .

[Gao2019-10] Jump up to: ^а ^б ^с Гао, Сян; Галликкио, Эмилио; Ройтберг, Адриан (2019). «Обобщенное распределение Больцмана — единственное распределение, в котором энтропия Гиббса-Шеннона равна термодинамической энтропии» . Журнал химической физики . 151 (3): 034113. arXiv : 1903.02121 . Бибкод : 2019JChPh.151c4113G . дои : 10.1063/1.5111333 . ПМИД 31325924 . S2CID 118981017 .

[Gao2022-11] Jump up to: ^а ^б Гао, Сян (март 2022 г.). «Математика теории ансамбля» . Результаты по физике . 34 : 105230. arXiv : 2006.00485 . Бибкод : 2022ResPh..3405230G . дои : 10.1016/j.rinp.2022.105230 . S2CID 221978379 .

[12] Классический пример этого — магнитное упорядочение . Системы невзаимодействующих спинов демонстрируют парамагнитное поведение, которое можно понять с помощью одночастичного канонического ансамбля (что приводит к функции Бриллюэна ). Системы взаимодействующих спинов могут демонстрировать гораздо более сложное поведение, такое как ферромагнетизм или антиферромагнетизм .

[Park,_J.-W._2012-13] Парк, Дж.-В., Ким, К.У. и Айсард, В. (2012) Распределение разрешений на торговлю выбросами с использованием распределения Больцмана. Физика А 391: 4883–4890.

[14] Сложная проблема справедливого распределения . Блог Technology Review . 17 августа 2011 г. Цитирует и резюмирует Пак, Ким и Айсард (2012).

[15] Амемия, Такеши (1985). «Мультиномиальная логит-модель» . Продвинутая эконометрика . Оксфорд: Бэзил Блэквелл. стр. 295–299. ISBN 0-631-13345-3 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]