Распределение ци

См. Также: Распределение хи-квадрат.

тратить

Функция плотности вероятности
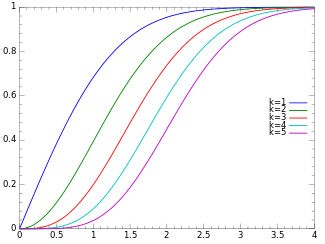
Кумулятивная функция распределения
Обозначения	$\chi (k)\;$ или $\chi _{k}\!$
Параметры	$k>0\,$ (степени свободы)
Поддерживать	$x\in [0,\infty )$
PDF	${\frac {1}{2^{(k/2)-1}\Gamma (k/2)}}\;x^{k-1}e^{-x^{2}/2}$
CDF	$P(k/2,x^{2}/2)\,$
Иметь в виду	$\mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}$
медиана	$\approx {\sqrt {k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}}}$
Режим	${\sqrt {k-1}}\,$ для $k\geq 1$
Дисперсия	$\sigma ^{2}=k-\mu ^{2}\,$
асимметрия	$\gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})$
Избыточный эксцесс	${\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})$
Энтропия	$\ln(\Gamma (k/2))+\,$ ${\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))$
МГФ	Сложный (см. текст)
CF	Сложный (см. текст)

В теории вероятностей и статистике распределение хи представляет собой непрерывное распределение вероятностей по неотрицательной действительной линии. Это распределение положительного квадратного корня из суммы квадратов независимых гауссовских случайных величин . Эквивалентно, это распределение евклидова расстояния между многомерной гауссовой случайной величиной и началом координат. Таким образом, это связано с распределением хи-квадрат , описывая распределение положительных квадратных корней переменной, подчиняющейся распределению хи-квадрат.

Если $Z_{1},\ldots ,Z_{k}$ являются $k$ независимые, нормально распределенные случайные величины со средним значением 0 и стандартным отклонением 1, то статистика

$Y={\sqrt {\sum _{i=1}^{k}Z_{i}^{2}}}$

распределяется в соответствии с распределением ци. Распределение хи имеет один положительный целочисленный параметр. $k$, который определяет степени свободы (т.е. количество случайных величин $Z_{i}$).

Наиболее известными примерами являются распределение Рэлея (распределение хи с двумя степенями свободы ) и распределение Максвелла – Больцмана скоростей молекул в идеальном газе (распределение хи с тремя степенями свободы).

Определения

плотности

Функция плотности вероятности (pdf) хи-распределения равна

$f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geq 0;\\0,&{\text{otherwise}}.\end{cases}}$

где $\Gamma (z)$ это гамма-функция .

распределения

Кумулятивная функция распределения определяется выражением:

$F(x;k)=P(k/2,x^{2}/2)\,$

где $P(k,x)$ – регуляризованная гамма-функция .

Генерирующие функции

определяется Создающая момент функция выражением:

$M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+t{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right),$

где $M(a,b,z)$ Куммера — вырожденная гипергеометрическая функция . Характеристическая функция определяется выражением:

$\varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+it{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right).$

Свойства

Моменты

Необработанные моменты тогда даются следующим образом:

$\mu _{j}=\int _{0}^{\infty }f(x;k)x^{j}\mathrm {d} x=2^{j/2}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+j)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}$

где $\ \Gamma (z)\$ это гамма-функция . Итак, первые несколько сырых моментов таковы:

$\mu _{1}={\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+1)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}$

$\mu _{2}=k\ ,$

$\mu _{3}=2{\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+3)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}=(k+1)\ \mu _{1}\ ,$

$\mu _{4}=(k)(k+2)\ ,$

$\mu _{5}=4{\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k\!+\!5)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}=(k+1)(k+3)\ \mu _{1}\ ,$

$\mu _{6}=(k)(k+2)(k+4)\ ,$

где самые правые выражения получены с использованием рекуррентного соотношения для гамма-функции:

$\Gamma (x+1)=x\ \Gamma (x)~.$

Из этих выражений мы можем вывести следующие соотношения:

Иметь в виду: $\mu ={\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+1)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}\ ,$ что близко к ${\sqrt {k-{\tfrac {1}{2}}\ }}\$ для большого k .

Разница: $V=k-\mu ^{2}\ ,$ который приближается $\ {\tfrac {1}{2}}\$ по мере увеличения k .

Асимметрия: $\gamma _{1}={\frac {\mu }{\ \sigma ^{3}\ }}\left(1-2\sigma ^{2}\right)~.$

Эксцесс эксцесса: $\gamma _{2}={\frac {2}{\ \sigma ^{2}\ }}\left(1-\mu \ \sigma \ \gamma _{1}-\sigma ^{2}\right)~.$

Энтропия

Энтропия определяется:

$S=\ln(\Gamma (k/2))+{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi ^{0}(k/2))$

где $\psi ^{0}(z)$ – полигамма-функция .

Большое n-приближение

Мы находим большое n=k+1 приближение среднего и дисперсии распределения хи. Это применимо, например, для определения распределения стандартного отклонения выборки из нормально распределенной совокупности, где n — размер выборки.

Среднее значение тогда:

$\mu ={\sqrt {2}}\,\,{\frac {\Gamma (n/2)}{\Gamma ((n-1)/2)}}$

Используя формулу дублирования Лежандра, запишем:

$2^{n-2}\,\Gamma ((n-1)/2)\cdot \Gamma (n/2)={\sqrt {\pi }}\Gamma (n-1)$,

так что:

$\mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {(\Gamma (n/2))^{2}}{\Gamma (n-1)}}$

Используя аппроксимацию Стирлинга для гамма-функции, мы получаем следующее выражение для среднего значения:

$\mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}$

$=(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]$

$={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{2n}}+O({\frac {1}{n^{2}}})\right]\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]$

$={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]$

Таким образом, дисперсия равна:

$V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}}\,\cdot \left[1+O({\frac {1}{n}})\right]$

Связанные дистрибутивы

• Если $X\sim \chi _{k}$ затем $X^{2}\sim \chi _{k}^{2}$ ( распределение хи-квадрат )
• $\chi _{1}\sim \mathrm {HN} (1)\,$ ( полунормальное распределение ), т.е. если $X\sim N(0,1)\,$ затем $|X|\sim \chi _{1}\,$, и если $Y\sim \mathrm {HN} (\sigma )\,$ для любого $\sigma >0\,$ затем ${\tfrac {Y}{\sigma }}\sim \chi _{1}\,$
• $\chi _{2}\sim \mathrm {Rayleigh} (1)\,$ ( распределение Рэлея ) и если $Y\sim \mathrm {Rayleigh} (\sigma )\,$ для любого $\sigma >0\,$ затем ${\tfrac {Y}{\sigma }}\sim \chi _{2}\,$
• $\chi _{3}\sim \mathrm {Maxwell} (1)\,$ ( распределение Максвелла ) и если $Y\sim \mathrm {Maxwell} (a)\,$ для любого $a>0\,$ затем ${\tfrac {Y}{a}}\sim \chi _{3}\,$
• $\|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|_{2}\sim \chi _{k}$, евклидова норма стандартного нормального случайного вектора с $k$ размеров, распределяется в соответствии с распределением ци с $k$ степени свободы
• Распределение ци является частным случаем обобщенного гамма-распределения , распределения Накагами или нецентрального распределения ци.
• $\lim _{k\to \infty }{\tfrac {\chi _{k}-\mu _{k}}{\sigma _{k}}}{\xrightarrow {d}}\ N(0,1)\,$ ( Нормальное распределение )
• Среднее значение распределения ци (масштабированное квадратным корнем из $n-1$) дает поправочный коэффициент при несмещенной оценке стандартного отклонения нормального распределения .

Различные распределения хи и хи-квадрат

Имя	Статистика
распределение хи-квадрат	$\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}$
нецентральное распределение хи-квадрат	$\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}$
распределение ци	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}$
нецентральное распределение ци	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}$

См. также

• Распределение Накагами

Ссылки

• Марта Л. Абелл, Джеймс П. Бразелтон, Джон Артур Рафтер, Джон А. Рафтер, Статистика в Mathematica (1999), 237f.
• Ян В. Гуч, Энциклопедический словарь полимеров, том. 1 (2010), Приложение Е, с. 972 .

Внешние ссылки

• http://mathworld.wolfram.com/ChiDistribution.html