Круговое равномерное распределение

В теории вероятностей и статистике направлений круговое равномерное распределение — это распределение вероятностей на единичном круге, плотность которого одинакова для всех углов.

Описание

Определение

Функция плотности вероятности (pdf) кругового равномерного распределения, например, с $\theta \in [0,2\pi )$ , является:

f_{UC}(\theta )={\frac {1}{2\pi }}.

Моменты относительно параметризации

Рассмотрим круговую переменную $z=e^{i\theta }$ с $z=1$ под базовым углом $\theta =0$ . В этих терминах все круговые моменты кругового равномерного распределения равны нулю, за исключением $m_{0}$ :

\langle z^{n}\rangle =\delta _{n}

где $\delta _{n}$ – символ дельты Кронекера .

Описательная статистика

Здесь средний угол не определен, а длина среднего результирующего равна нулю.

R=|\langle z^{n}\rangle |=0\,

Распределение среднего значения

Моделирование Монте-Карло по 10 000 точек распределения выборочного среднего кругового равномерного распределения для N = 3.

Выборочное среднее из набора N измерений $z_{n}=e^{i\theta _{n}}$ полученный из кругового равномерного распределения, определяется как:

{\overline {z}}={\frac {1}{N}}\sum _{n=1}^{N}z_{n}={\overline {C}}+i{\overline {S}}={\overline {R}}e^{i{\overline {\theta }}}

где средние синус и косинус равны: ^[1]

{\overline {C}}={\frac {1}{N}}\sum _{n=1}^{N}\cos(\theta _{n})\qquad \qquad {\overline {S}}={\frac {1}{N}}\sum _{n=1}^{N}\sin(\theta _{n})

и средняя результирующая длина равна:

{\overline {R}}^{2}=|{\overline {z}}|^{2}={\overline {C}}^{2}+{\overline {S}}^{2}

а средний угол:

{\overline {\theta }}=\mathrm {Arg} ({\overline {z}}).\,

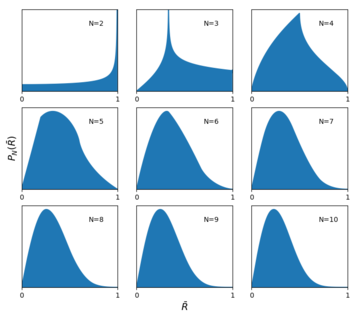
Выборочное среднее для кругового равномерного распределения будет сконцентрировано около нуля и станет более концентрированным по мере N. увеличения Распределение выборочного среднего для равномерного распределения определяется следующим образом: ^[2]

{\frac {1}{(2\pi )^{N}}}\int _{\Gamma }\prod _{n=1}^{N}d\theta _{n}=P({\overline {R}})P({\overline {\theta }})\,d{\overline {R}}\,d{\overline {\theta }}

где $\Gamma \,$ состоит из интервалов $2\pi$ в переменных, при условии, что ${\overline {R}}$ и ${\overline {\theta }}$ постоянны или, альтернативно, что ${\overline {C}}$ и ${\overline {S}}$ постоянны. Распределение угла $P({\overline {\theta }})$ является однородным

P({\overline {\theta }})={\frac {1}{2\pi }}

и распределение ${\overline {R}}$ дается: ^[2]

P_{N}({\overline {R}})=N^{2}{\overline {R}}\int _{0}^{\infty }J_{0}(N{\overline {R}}\,t)J_{0}(t)^{N}t\,dt

где $J_{0}$ – функция Бесселя нулевого порядка. Для приведенного выше интеграла не существует известного общего аналитического решения, и его трудно оценить из-за большого количества колебаний подынтегральной функции. На рисунке показано 10 000-точечное моделирование распределения среднего значения Монте-Карло для N = 3.

В некоторых особых случаях приведенный выше интеграл можно вычислить:

P_{2}({\overline {R}})={\frac {2}{\pi {\sqrt {1-{\overline {R}}^{2}}}}}.

Для больших N распределение среднего значения можно определить из центральной предельной теоремы для статистики направлений . Поскольку углы распределены равномерно, отдельные синусы и косинусы углов будут распределяться как:

P(u)du={\frac {1}{\pi }}\,{\frac {du}{\sqrt {1-u^{2}}}}

где $u=\cos \theta _{n}\,$ или $\sin \theta _{n}\,$ . Отсюда следует, что они будут иметь нулевое среднее значение и дисперсию 1/2. По центральной предельной теореме в пределе N больших ${\overline {C}}\,$ и ${\overline {S}}\,$ , являясь суммой большого количества iid , будет нормально распределяться со средним нулевым значением и дисперсией $1/2N$ . Средняя результирующая длина ${\overline {R}}\,$ , являющийся квадратным корнем суммы квадратов двух нормально распределенных независимых переменных, будет иметь Хи-распределение с двумя степенями свободы (т.е. Рэлеевское распределение ) и дисперсию $1/2N$ :

\lim _{N\rightarrow \infty }P_{N}({\overline {R}})=2N{\overline {R}}\,e^{-N{\overline {R}}^{2}}.

Энтропия

Дифференциальная информационная энтропия равномерного распределения просто

H_{U}=-\int _{\Gamma }{\frac {1}{2\pi }}\ln \left({\frac {1}{2\pi }}\right)\,d\theta =\ln(2\pi )

где $\Gamma$ любой интервал длины $2\pi$ . Это максимальная энтропия, которую может иметь любое круговое распределение.

См. также

Завернутое распространение

Ссылки

^ «Формирование луча для радиолокационных приложений с использованием случайных решеток с круговой конусностью - Публикация конференции IEEE». дои : 10.1109/RADAR.2017.7944181 . S2CID 38429370 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Jump up to: ^а ^б Джаммаламадака, С. Рао; Сенгупта, А. (2001). Темы круговой статистики . Мировое научное издательство. ISBN 978-981-02-3778-3 .

[1] «Формирование луча для радиолокационных приложений с использованием случайных решеток с круговой конусностью - Публикация конференции IEEE». дои : 10.1109/RADAR.2017.7944181 . S2CID 38429370 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[Jam-2] Jump up to: ^а ^б Джаммаламадака, С. Рао; Сенгупта, А. (2001). Темы круговой статистики . Мировое научное издательство. ISBN 978-981-02-3778-3 .

[1]

[2]