Gauss–Kuzmin distribution

Gauss–Kuzmin

Функция массы вероятности
Кумулятивная функция распределения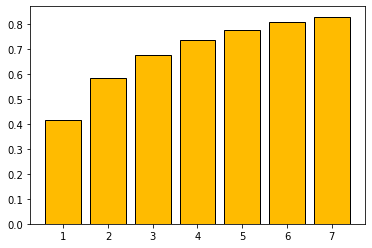
Параметры	(никто)
Поддерживать	$k\in \{1,2,\ldots \}$
ПМФ	$-\log _{2}\left[1-{\frac {1}{(k+1)^{2}}}\right]$
CDF	$1-\log _{2}\left({\frac {k+2}{k+1}}\right)$
Иметь в виду	$+\infty$
медиана	$2\,$
Режим	$1\,$
Дисперсия	$+\infty$
асимметрия	(не определено)
Избыточный эксцесс	(не определено)
Энтропия	3.432527514776...

В математике распределение Гаусса -Кузьмина представляет собой дискретное распределение вероятностей , которое возникает как предельное распределение вероятностей коэффициентов в в цепную дробь разложении случайной величины, равномерно распределенной в (0, 1). Распределение названо в честь Карла Фридриха Гаусса , который вывел его около 1800 года. и Родион Кузьмин , который дал оценку скорости конвергенции в 1929 году. Оно определяется функцией массы вероятности

$p(k)=-\log _{2}\left(1-{\frac {1}{(1+k)^{2}}}\right)~.$

Gauss–Kuzmin theorem

Позволять

$x={\cfrac {1}{k_{1}+{\cfrac {1}{k_{2}+\cdots }}}}$

— разложение в цепную дробь случайного числа x, равномерно распределенного в (0, 1). Затем

$\lim _{n\to \infty }\mathbb {P} \left\{k_{n}=k\right\}=-\log _{2}\left(1-{\frac {1}{(k+1)^{2}}}\right)~.$

Эквивалентно, пусть

$x_{n}={\cfrac {1}{k_{n+1}+{\cfrac {1}{k_{n+2}+\cdots }}}}~;$

затем

$\Delta _{n}(s)=\mathbb {P} \left\{x_{n}\leq s\right\}-\log _{2}(1+s)$

стремится к нулю, поскольку n стремится к бесконечности.

Скорость сходимости

В 1928 году Кузьмин дал привязку.

$|\Delta _{n}(s)|\leq C\exp(-\alpha {\sqrt {n}})~.$

в 1929 году Поль Леви улучшил его до

$|\Delta _{n}(s)|\leq C\,0.7^{n}~.$

Позже Эдуард Вирсинг показал что для λ = 0,30366... ​​( константа Гаусса–Кузьмина–Вирсинга ) предел

$\Psi (s)=\lim _{n\to \infty }{\frac {\Delta _{n}(s)}{(-\lambda )^{n}}}$

существует для любого s из [0, 1], а функция Ψ ( s ) аналитична и удовлетворяет условию Ψ (0) = Ψ (1) = 0. Дальнейшие оценки были доказаны К.И. Бабенко .

См. также

• постоянная Хинчина
• постоянная Леви