постоянная Хинчина

В теории чисел Александр Яковлевич Хинчин доказал, что почти для всех действительных чисел x коэффициенты a _i в цепную дробь разложения x имеют конечное среднее геометрическое , не зависящее от значения x и известное как константа Хинчина .

То есть для

x=a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{a_{3}+{\cfrac {1}{\ddots }}}}}}}}\;

это почти всегда правда, что

\lim _{n\rightarrow \infty }\left(a_{1}a_{2}...a_{n}\right)^{1/n}=K_{0}

где $K_{0}$ постоянная Хинчина

K_{0}=\prod _{r=1}^{\infty }{\left(1+{1 \over r(r+2)}\right)}^{\log _{2}r}\approx 2.6854520010\dots

(последовательность A002210 в OEIS )

(с $\prod$ обозначая произведение по всем членам последовательности ).

Хотя почти все числа удовлетворяют этому свойству, оно не было доказано ни для одного действительного числа , специально созданного для этой цели. Среди чисел, чьи разложения в цепные дроби, по-видимому, действительно обладают этим свойством (на основании численных данных), есть π , константа Эйлера-Машерони γ, константа Апери ζ(3) и сама константа Хинчина. Однако это недоказано.

Среди чисел x, разложение цепной дроби которых, как известно, не обладает этим свойством, есть рациональные числа , корни квадратных уравнений (включая золотое сечение Φ и квадратные корни целых чисел) и основание натурального логарифма e .

Хинчин в старой математической литературе иногда пишется как Хинчин (французская транслитерация русского Хинчин).

Эскиз доказательства

Представленное здесь доказательство было подготовлено Чеславом Рыль-Нардзевским. ^{[ 1 ]} и оно намного проще, чем оригинальное доказательство Хинчина, в котором не использовалась эргодическая теория .

Так как первый коэффициент а ₀ цепной дроби х не играет роли в теореме Хинчина и поскольку рациональные числа имеют меру Лебега нулевую, то мы сводимся к изучению иррациональных чисел в единичном интервале , т. е. в $I=[0,1]\setminus \mathbb {Q}$ . Эти числа находятся в биекции с бесконечными цепными дробями вида [0; a ₁ , a ₂ , ...], которые мы просто пишем [ a ₁ , a ₂ , ...], где a ₁ , a ₂ , ... — положительные целые числа . Определим преобразование T : I → I с помощью

T([a_{1},a_{2},\dots ])=[a_{2},a_{3},\dots ].\,

Преобразование T называется оператором Гаусса–Кузьмина–Вирсинга . Для каждого борелевского подмножества E из I мы также определяем Гаусса–Кузьмина меру E

\mu (E)={\frac {1}{\log 2}}\int _{E}{\frac {dx}{1+x}}.

Тогда µ — вероятностная мера на σ -алгебре борелевских подмножеств I . Мера µ эквивалентна , но мере Лебега на I обладает дополнительным свойством: преобразование T сохраняет меру µ . Более того, можно доказать, что T — эргодическое преобразование измеримого пространства I, наделенное вероятностной мерой µ (это самая трудная часть доказательства). Тогда эргодическая теорема утверждает, что для любой µ - интегрируемой функции f на I среднее значение $f\left(T^{k}x\right)$ почти у всех одинаково $x$ :

\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=0}^{n-1}(f\circ T^{k})(x)=\int _{I}fd\mu \quad {\text{for }}\mu {\text{-almost all }}x\in I.

Применяя это к функции, определяемой формулой f ([ a ₁ , a ₂ , ...]) = log( a ₁ ), мы получаем, что

\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n}\log(a_{k})=\int _{I}f\,d\mu =\sum _{r=1}^{\infty }\log(r){\frac {\log {\bigl (}1+{\frac {1}{r(r+2)}}{\bigr )}}{\log 2}}

для почти всех [ a ₁ , a ₂ , ...] в I при n → ∞.

Взяв экспоненту с обеих сторон, получим слева среднее геометрическое первых n коэффициентов цепной дроби, а справа константу Хинчина.

Выражения серии

Константу Хинчина можно выразить в виде рационального дзета-ряда в виде ^{[ 2 ]}

\log K_{0}={\frac {1}{\log 2}}\sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{n}}\sum _{k=1}^{2n-1}{\frac {(-1)^{k+1}}{k}}

или, отделив члены ряда,

\log K_{0}={\frac {1}{\log 2}}\left[-\sum _{k=2}^{N}\log \left({\frac {k-1}{k}}\right)\log \left({\frac {k+1}{k}}\right)+\sum _{n=1}^{\infty }{\frac {\zeta (2n,N+1)}{n}}\sum _{k=1}^{2n-1}{\frac {(-1)^{k+1}}{k}}\right]

где N — целое число, фиксированное, а ζ( s , n ) — комплексная дзета-функция Гурвица . Оба ряда сильно сходятся, поскольку ζ( n ) − 1 быстро приближается к нулю при больших n . Разложение также может быть дано в терминах дилогарифма :

\log K_{0}=\log 2+{\frac {1}{\log 2}}\left[{\mbox{Li}}_{2}\left({\frac {-1}{2}}\right)+{\frac {1}{2}}\sum _{k=2}^{\infty }(-1)^{k}{\mbox{Li}}_{2}\left({\frac {4}{k^{2}}}\right)\right].

Гёльдер означает

Константу Хинчина можно рассматривать как первую в ряду средних Гёльдера членов цепных дробей. Для произвольной серии { a _n } среднее Гёльдера порядка p этой серии определяется выражением

K_{p}=\lim _{n\to \infty }\left[{\frac {1}{n}}\sum _{k=1}^{n}a_{k}^{p}\right]^{1/p}.

Когда { a _n } являются членами разложения цепной дроби, константы задаются формулой

K_{p}=\left[\sum _{k=1}^{\infty }-k^{p}\log _{2}\left(1-{\frac {1}{(k+1)^{2}}}\right)\right]^{1/p}.

Это получается путем взятия p -го среднего значения в сочетании с распределением Гаусса – Кузьмина . Это конечно, когда $p<1$ .

Среднее арифметическое расходится: $\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n}a_{k}=K_{1}=+\infty$ , и поэтому коэффициенты становятся сколь угодно большими: $\limsup _{n}a_{n}=+\infty$ .

Значение K ₀ получается в пределе p → 0.

Гармоническое среднее ( p = −1) равно

K_{-1}=1.74540566240\dots

(последовательность A087491 в OEIS ).

Открытые проблемы

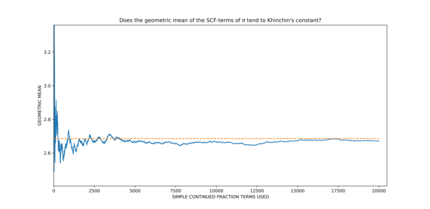
$π$ , константа Эйлера-Машерони γ и сама константа Хинчина, основанная на численных данных, ^{[ 3 ]}^{[ 4 ]} Считается, что они относятся к числам, среднее геометрическое коэффициентов которых a _i в их разложении в цепную дробь стремится к константе Хинчина. Однако ни один из этих пределов не был строго установлен.
Неизвестно, является ли константа Хинчина рациональным, алгебраическим иррациональным или трансцендентным числом. ^{[ 5 ]}

См. также

Ссылки

^ Рилл-Нардзевский, Чеслав (1951), «Об эргодических теоремах II (эргодическая теория цепных дробей)», Studia Mathematica , 12 : 74–79, doi : 10.4064/sm-12-1-74-79
^ Bailey, Borwein & Crandall, 1997. В этой статье для дзета-функции Гурвица используется немного нестандартное определение.
^ Вайсштейн, Эрик В. «Постоянная непрерывная дробь Эйлера-Машерони» . mathworld.wolfram.com . Проверено 23 марта 2020 г.
^ Вайсштейн, Эрик В. «Непрерывная дробь Пи» . mathworld.wolfram.com . Проверено 23 марта 2020 г.
^ Вайсштейн, Эрик В. «Постоянная Хинчина» . Математический мир .

Дэвид Х. Бэйли; Джонатан М. Борвейн; Ричард Э. Крэндалл (1995). «О постоянной Хинчина» (PDF) . Математика вычислений . 66 (217): 417–432. дои : 10.1090/s0025-5718-97-00800-4 .
Джонатан М. Борвейн; Дэвид М. Брэдли; Ричард Э. Крэндалл (2000). «Вычислительные стратегии для дзета-функции Римана» (PDF) . Дж. Компьютер. Прил. Математика . 121 (1–2): 11. Бибкод : 2000JCoAM.121..247B . дои : 10.1016/s0377-0427(00)00336-8 .

Томас Витинг (2007). «Последовательность Хинчина» . Труды Американского математического общества . 136 (3): 815–824. дои : 10.1090/S0002-9939-07-09202-7 .

Александр Я. Хинчин (1997). Продолжительные дроби . Нью-Йорк: Dover Publications.

Внешние ссылки

[1] Рилл-Нардзевский, Чеслав (1951), «Об эргодических теоремах II (эргодическая теория цепных дробей)», Studia Mathematica , 12 : 74–79, doi : 10.4064/sm-12-1-74-79

[2] Bailey, Borwein & Crandall, 1997. В этой статье для дзета-функции Гурвица используется немного нестандартное определение.

[3] Вайсштейн, Эрик В. «Постоянная непрерывная дробь Эйлера-Машерони» . mathworld.wolfram.com . Проверено 23 марта 2020 г.

[4] Вайсштейн, Эрик В. «Непрерывная дробь Пи» . mathworld.wolfram.com . Проверено 23 марта 2020 г.

[5] Вайсштейн, Эрик В. «Постоянная Хинчина» . Математический мир .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]