Иррациональное число

Число √ 2 иррационально.

В математике иррациональными числами ( ин- + рациональные ) являются все действительные числа , которые не являются рациональными числами . То есть иррациональные числа не могут быть выражены как отношение двух целых чисел . Когда отношение длин двух отрезков линии является иррациональным числом, отрезки линии также описываются как несоизмеримые , то есть у них нет общей «меры», то есть нет ни длины («меры»), ни длины. независимо от того, насколько он короткий, его можно использовать для выражения длин обоих данных сегментов как целых чисел, кратных самому себе.

Среди иррациональных чисел — отношение π длины окружности к ее диаметру, число Эйлера e , золотое сечение φ и квадратный корень из двух . Фактически, все квадратные корни из натуральных чисел , кроме полных квадратов , иррациональны.

Как и все действительные числа, иррациональные числа могут быть выражены в позиционных обозначениях , особенно в виде десятичных чисел. В случае иррациональных чисел десятичное разложение не заканчивается и не заканчивается повторяющейся последовательностью . Например, десятичное представление числа π начинается с 3,14159, но никакое конечное число цифр не может точно представлять число π и не повторяется. И наоборот, десятичное расширение, которое заканчивается или повторяется, должно быть рациональным числом. Это доказуемые свойства рациональных чисел и позиционных систем счисления, которые не используются в качестве определений в математике.

Иррациональные числа также можно выразить в виде бесконечных цепных дробей (которые в некоторых случаях являются периодическими ) и многими другими способами.

Из доказательства Кантора действительных чисел несчетности и счетности рациональных чисел следует, что почти все действительные числа иррациональны.

История

Набор действительных чисел (R), включающих рациональные числа (Q), включающих целые числа (Z), включающих натуральные числа (N). Действительные числа включают также иррациональные (R\Q).

Древняя Греция

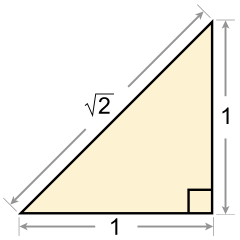
Первое доказательство существования иррациональных чисел обычно приписывают пифагорейцу ( возможно, Гиппасу из Метапонта ), который, вероятно, обнаружил их, определяя стороны пентаграммы . Метод Пифагора утверждал бы, что должна быть какая-то достаточно маленькая неделимая единица, которая могла бы равномерно вписаться как в одну из этих длин, так и в другую. Однако Гиппас в V веке до нашей эры смог прийти к выводу, что не существует общей единицы измерения и что утверждение о таком существовании является противоречием. Он сделал это, продемонстрировав, что если гипотенуза равнобедренного прямоугольного треугольника действительно соизмерима с катетом, то одна из длин, измеренных в этой единице измерения, должна быть одновременно нечетной и четной, что невозможно. Его рассуждения таковы:

• Начните с равнобедренного прямоугольного треугольника с длинами сторон целых чисел a , b и c . Отношение гипотенузы к катету обозначается как c : b .
• Предположим, что a , b и c представлены в наименьших возможных размерах ( т.е. у них нет общих множителей).
• По теореме Пифагора : c ² = а ² + б ² = б ² + б ² = 2 б ² . (Поскольку треугольник равнобедренный, a = b ).
• Поскольку c ² = 2 б ² , с ² делится на 2 и, следовательно, четно.
• Поскольку c ² четно, c должно быть четным.
• Поскольку c четно, деление c на 2 дает целое число. Пусть y будет этим целым числом ( c = 2 y ).
• Возведение в квадрат обеих частей c = 2 y дает c ² = ( 2г ) ² или с ² = 4 года ² .
• Замена 4 года ² для с ² в первом уравнении ( c ² = 2 б ² ) дает нам 4 года ² = 2 б ² .
• Деление на 2 дает 2 y ² = б ² .
• Поскольку y целое число и 2 y ² = б ² , б ² делится на 2 и, следовательно, четно.
• Поскольку б ² четно, b должно быть четным.
• Мы только что показали, что b и c должны быть четными. Следовательно, у них есть общий делитель, равный 2. Однако это противоречит предположению, что у них нет общих делителей. Это противоречие доказывает, что c и b не могут быть одновременно целыми числами и, следовательно, существование числа, которое не может быть выражено как отношение двух целых чисел.

Греческие математики называли это соотношение несоизмеримых величин alogos , или невыразимым. Гиппаса, однако, не хвалили за его усилия: согласно одной легенде, он сделал свое открытие, находясь в море, и впоследствии был выброшен за борт своими собратьями-пифагорейцами «за то, что создал во вселенной элемент, который отрицал... доктрину». что все явления во Вселенной можно свести к целым числам и их отношениям». Другая легенда гласит, что Гиппас был просто сослан за это откровение. Какими бы ни были последствия для самого Гиппаса, его открытие поставило очень серьезную проблему для пифагорейской математики, поскольку разрушило представление о нераздельности чисел и геометрии; основу их теории.

Открытие несоизмеримых отношений указывало на еще одну проблему, стоявшую перед греками: отношение дискретного к непрерывному. Это было обнаружено Зеноном Элейским , который поставил под сомнение концепцию, согласно которой величины дискретны и состоят из конечного числа единиц заданного размера. Прежние греческие концепции диктовали, что они обязательно должны быть таковыми, поскольку «целые числа представляют собой дискретные объекты, а соизмеримое соотношение представляет собой отношение между двумя наборами дискретных объектов». но Зенон обнаружил, что на самом деле «[количества] вообще не являются дискретным набором единиц; именно поэтому появляются отношения несоизмеримых [количеств]... Другими словами, [Q] величины непрерывны». Это означает, что, вопреки распространенному в то время представлению, не может быть неделимой, наименьшей единицы измерения какой-либо величины. Фактически, эти количественные деления обязательно должны быть бесконечными . Например, рассмотрим отрезок линии: этот отрезок можно разделить пополам, ту половину разделить пополам, половину половины пополам и так далее. Этот процесс может продолжаться бесконечно, поскольку всегда остается еще одна половина, которую нужно разделить. Чем больше раз отрезок делится пополам, тем ближе единица измерения приближается к нулю, но она никогда не достигает точного нуля. Именно это и стремился доказать Зенон. Он стремился доказать это, сформулировав четыре парадокса , демонстрировавшие противоречия, присущие математической мысли того времени. Хотя парадоксы Зенона точно продемонстрировали недостатки современных математических концепций, они не рассматривались как доказательство альтернативы. По мнению греков, опровержение обоснованности одной точки зрения не обязательно доказывало обоснованность другой, и поэтому необходимо было провести дальнейшее исследование.

Следующий шаг был сделан Евдоксом Книдским , который формализовал новую теорию пропорций, учитывающую как соизмеримые, так и несоизмеримые величины. Центральным в его идее было различие между величиной и числом. Величина «...не была числом, а обозначала такие сущности, как отрезки линий, углы, площади, объемы и время, которые могли меняться, как мы бы сказали, непрерывно. Величины противопоставлялись числам, которые прыгали от одного значения к другому». другой, от 4 до 5". Числа состоят из какой-то мельчайшей неделимой единицы, тогда как величины бесконечно сокращаемы. Поскольку величинам не было присвоено никаких количественных значений, Евдокс смог объяснить как соизмеримые, так и несоизмеримые отношения, определив соотношение через его величину, а пропорцию - как равенство между двумя отношениями. Исключив из уравнения количественные значения (числа), он избежал ловушки, заключающейся в необходимости выражать иррациональное число как число. «Теория Евдокса позволила греческим математикам добиться огромного прогресса в геометрии, предоставив необходимое логическое обоснование для несоизмеримых отношений». Эта несоизмеримость рассматривается в «Началах» Евклида, книга X, предложение 9. Только когда Евдокс разработал теорию пропорций, которая принимала во внимание как иррациональные, так и рациональные отношения, было создано прочное математическое обоснование иррациональных чисел.

В результате различения числа и величины геометрия стала единственным методом, способным учитывать несоизмеримые отношения. Поскольку предыдущие численные основы все еще были несовместимы с концепцией несоизмеримости, греческое внимание сместилось с числовых концепций, таких как алгебра, и сосредоточилось почти исключительно на геометрии. Фактически, во многих случаях алгебраические концепции были переформулированы в геометрические термины. Это может объяснить, почему мы до сих пор воспринимаем x ² и х ³ как x в квадрате и x в кубе вместо x во второй степени и x в третьей степени. В работе Зенона, посвященной несоизмеримым масштабам, также решающее значение имело фундаментальное внимание к дедуктивным рассуждениям, возникшее в результате фундаментального разрушения ранней греческой математики. Осознание того, что некоторые основные концепции существующей теории расходятся с реальностью, потребовало полного и тщательного исследования аксиом и предположений, лежащих в основе этой теории. Из-за этой необходимости Евдокс разработал свой метод исчерпания , своего рода доведение до абсурда , который «...установил дедуктивную организацию на основе явных аксиом...», а также «...подкрепил ранее принятое решение полагаться на о дедуктивном рассуждении для доказательства». Этот метод исчерпания является первым шагом в создании исчисления.

Теодор Киренский доказал иррациональность целых чисел до 17, но остановился на этом, вероятно, потому, что использованная им алгебра не могла быть применена к квадратному корню из 17.

Индия

Геометрические и математические проблемы, связанные с иррациональными числами, такими как квадратные корни, были решены очень рано, в ведический период в Индии. Ссылки на подобные расчеты есть в Самхитах , Брахманах и Шулба-сутрах (800 г. до н. э. или ранее).

Предполагается, что концепция иррациональности была неявно принята индийскими математиками с VII века до нашей эры, когда Манава (ок. 750–690 до н. э.) считал, что квадратные корни таких чисел, как 2 и 61, не могут быть точно определены. Историк Карл Бенджамин Бойер , однако, пишет, что «такие утверждения недостаточно обоснованы и вряд ли правдивы».

Позже в своих трактатах индийские математики писали об арифметике сурдов, включая сложение, вычитание, умножение, рационализацию, а также разделение и извлечение квадратных корней.

Такие математики, как Брахмагупта (в 628 г. н. э.) и Бхаскара I (в 629 г. н. э.), внесли вклад в эту область, как и другие математики, последовавшие за ними. В XII веке Бхаскара II оценил некоторые из этих формул и раскритиковал их, определив их ограничения.

В период с 14 по 16 века Мадхава из Сангамаграмы и школа астрономии и математики Кералы открыли бесконечный ряд для нескольких иррациональных чисел, таких как π , и некоторых иррациональных значений тригонометрических функций . Джйештхадева предоставил доказательства этих бесконечных серий в « Юктибхаше» .

Исламский мир

В средние века развитие алгебры мусульманскими математиками позволило рассматривать иррациональные числа как алгебраические объекты . Математики Ближнего Востока также объединили понятия « число » и « величина » в более общее представление о действительных числах , раскритиковали идею Евклида о пропорциях , разработали теорию сложных отношений и распространили понятие числа на отношения непрерывной величины. В своем комментарии к 10-й книге «Начал » персидский математик Аль -Махани (ум. 874/884) исследовал и классифицировал квадратичные иррациональные и кубические иррациональные числа. Он дал определения рациональным и иррациональным величинам, которые рассматривал как иррациональные числа. Он имел с ними дело свободно, но объяснял их в геометрических терминах следующим образом:

«Она будет рациональной (величиной), когда мы, например, скажем 10, 12, 3%, 6% и т. д., потому что ее значение ярко выражено и выражено количественно. То, что не рационально, то иррационально, и выговорить его невозможно. и представлять его значение количественно. Например: корни чисел, таких как 10, 15, 20, которые не являются квадратами, стороны чисел, которые не являются кубами и т. д. ».

В отличие от концепции Евклида о величинах как о линиях, Аль-Махани считал целые и дробные числа рациональными величинами, а квадратные и кубические корни - иррациональными величинами. Он также ввел арифметический подход к понятию иррациональности, приписывая иррациональным величинам следующее:

«их суммы или разности, или результаты их сложения с разумной величиной, или результаты вычитания такого рода величины из иррациональной, или разумной величины из нее».

Египетский степени математик Абу Камиль Шуджа ибн Аслам (ок. 850–930) был первым, кто принял иррациональные числа в качестве решений квадратных уравнений или в качестве коэффициентов в уравнении в виде квадратных корней и корней четвертой . В 10 веке иракский математик Аль-Хашими предоставил общие доказательства (а не геометрические демонстрации) иррациональных чисел, рассматривая умножение, деление и другие арифметические функции.

Многие из этих концепций были в конечном итоге приняты европейскими математиками спустя некоторое время после латинских переводов XII века . Аль-Хассар , марокканский математик из Феса , специализирующийся на исламском наследовании в XII веке, впервые упоминает использование дробной черты, где числители и знаменатели разделены горизонтальной чертой. В своем рассуждении он пишет: «..., например, если вам велят написать три пятых и треть пятой, напишите так: ${\frac {3\quad 1}{5\quad 3}}$." Такое же дробное обозначение вскоре появляется в работах Леонардо Фибоначчи в 13 веке.

Современный период

В 17 веке мнимые числа стали мощным инструментом в руках Авраама де Муавра и особенно Леонарда Эйлера . Завершение теории комплексных чисел в 19 веке повлекло за собой дифференциацию иррациональных чисел на алгебраические и трансцендентные числа , доказательство существования трансцендентных чисел и возрождение научного изучения теории иррациональных чисел, во многом игнорировавшегося со времен Евклида . В 1872 году были опубликованы теории Карла Вейерштрасса (его ученика Эрнста Коссака), Эдуарда Гейне ( «Журнал Крелля» , 74), Георга Кантора («Аннален», 5) и Рихарда Дедекинда . Мерэ взял в 1869 году ту же отправную точку, что и Гейне, но теорию обычно относят к 1872 году. Метод Вейерштрасса был полностью изложен Сальваторе Пинчерле в 1880 году. а книга Дедекинда получила дополнительную известность благодаря более поздним работам автора (1888 г.) и поддержке Пола Таннери (1894 г.). Вейерштрасс, Кантор и Гейне основывают свои теории на бесконечных рядах, а Дедекинд — на идее разреза (Шнитта) в системе всех рациональных чисел , разделяющего их на две группы, обладающие определёнными характеристическими свойствами. Эта тема получила более поздний вклад от рук Вейерштрасса, Леопольда Кронекера (Crelle, 101) и Шарля Мере .

Непрерывные дроби , тесно связанные с иррациональными числами (и благодаря Катальди, 1613 г.), привлекли внимание со стороны Эйлера, а в начале XIX века стали известны благодаря трудам Жозефа-Луи Лагранжа . Дирихле также внес свой вклад в общую теорию, как и многочисленные исследователи, внесшие вклад в применение этого предмета.

Иоганн Генрих Ламберт доказал (1761 г.), что π не может быть рациональным и что e ^н иррационально, если n рационально (если только n = 0). Хотя доказательство Ламберта часто называют неполным, современные оценки подтверждают его как удовлетворительное, и фактически для своего времени оно необычайно строгое. Адриен-Мари Лежандр (1794), после введения функции Бесселя – Клиффорда , предоставил доказательство того, что π ² иррационально, откуда сразу следует, что иррационально и π. Существование трансцендентных чисел впервые было установлено Лиувиллем (1844, 1851). Позже Георг Кантор (1873) доказал их существование другим методом , который показал, что каждый интервал действительных чисел содержит трансцендентные числа. Чарльз Эрмит (1873) впервые доказал трансцендентность е , а Фердинанд фон Линдеман (1882), исходя из выводов Эрмита, показал то же самое для π. Доказательство Линдеманна было значительно упрощено Вейерштрассом (1885 г.), еще больше Дэвидом Гильбертом (1893 г.) и, наконец, стало элементарным Адольфом Гурвицем. и Пол Гордан .

Примеры

Квадратные корни

Квадратный корень из 2 , вероятно, был первым числом, оказавшимся иррациональным. Золотое сечение – еще одно известное квадратичное иррациональное число. Квадратные корни всех натуральных чисел, которые не являются точными квадратами, иррациональны, и доказательство можно найти в квадратичных иррациональных числах .

Общие корни

Доказательство выше квадратный корень из двух можно обобщить, используя фундаментальную теорему арифметики . Это утверждает, что каждое целое число имеет уникальную разложение на простые числа. Используя его, мы можем показать, что если рациональное число не является целым числом, то никакая его целая степень не может быть целым числом, поскольку в самых простых терминах в знаменателе должно быть простое число , которое не делит на числитель, какую бы степень каждое из них ни возводили в степень. . Следовательно, если целое число не является точной k- й степенью другого целого числа, то k -й корень этого первого целого числа иррационален.

Логарифмы

Возможно, иррациональность чисел, которые легче всего доказать, — это определенные логарифмы . Вот доказательство от противного , что log ₂ 3 иррационально (log ₂ 3 ≈ 1,58 > 0).

Предположим, что log ₂ 3 рационален. Для некоторых натуральных чисел m и n мы имеем

$\log _{2}3={\frac {m}{n}}.$

Отсюда следует, что

$2^{m/n}=3$

$(2^{m/n})^{n}=3^{n}$

$2^{m}=3^{n}.$

Число 2, возведенное в любую положительную целую степень, должно быть четным (поскольку оно делится на 2), а число 3, возведенное в любую положительную целую степень, должно быть нечетным (поскольку ни один из его простых множителей не будет равен 2). Ясно, что целое число не может быть одновременно нечетным и четным: мы имеем противоречие. Единственное предположение, которое мы сделали, заключалось в том, что log ₂ 3 является рациональным (и поэтому выражается как частное целых чисел m / n с n ≠ 0). Противоречие означает, что это предположение должно быть ложным, т.е. log ₂ 3 иррационально и никогда не может быть выражено как частное целых чисел m / n с n ≠ 0.

Такие случаи, как log ₁₀ 2, можно рассматривать аналогично.

Типы

Иррациональное число может быть алгебраическим , то есть действительным корнем многочлена . с целыми коэффициентами Те, которые не являются алгебраическими, трансцендентны .

Алгебраический

Действительные алгебраические числа являются действительными решениями полиномиальных уравнений.

$p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0\;,$

где коэффициенты $a_{i}$ являются целыми числами и $a_{n}\neq 0$. Пример иррационального алгебраического числа: x ₀ = (2 ^1/2  + 1) ^1/3 . Очевидно, что он является алгебраическим, поскольку является корнем целочисленного многочлена ( x ³  − 1) ² = 2, что эквивалентно x ⁶ − 2 х ³ − 1 = 0. Этот многочлен не имеет рациональных корней, поскольку теорема о рациональном корне показывает, что единственные возможности — ±1, но x ₀ больше 1. Таким образом, x ₀ — иррациональное алгебраическое число. Алгебраических чисел счетно, так как целых многочленов счетно.

Трансцендентальный

Почти все иррациональные числа трансцендентны . Примеры: е  ^р и π  ^р , которые трансцендентны для всех ненулевых рациональных r.

Поскольку алгебраические числа образуют подполе действительных чисел, многие иррациональные действительные числа могут быть построены путем объединения трансцендентных и алгебраических чисел. Например, 3 π + 2, π + √ 2 и e √ 3 иррациональны (и даже трансцендентны).

Десятичные расширения

Десятичное разложение иррационального числа никогда не повторяется (это означает, что десятичное разложение не повторяет одно и то же число или последовательность чисел) и не заканчивается (это означает, что не существует конечного числа ненулевых цифр), в отличие от любого рационального числа. То же самое верно для двоичных , восьмеричных или шестнадцатеричных расширений и вообще для расширений во всех позиционных обозначениях с натуральными основаниями.

Чтобы показать это, предположим, что мы делим целые числа n на m (где m не равно нулю). Когда длинное деление применяется к делению n на m никогда не может быть , остаток больше или равен m . Если в остатке появляется 0, десятичное разложение прекращается. Если 0 никогда не встречается, то алгоритм может выполнить не более m − 1 шагов, не используя остаток более одного раза. После этого должен повториться остаток, а затем повторяется десятичное разложение.

И наоборот, предположим, что мы столкнулись с повторяющейся десятичной дробью , мы можем доказать, что она является дробью двух целых чисел. Например, рассмотрим:

$A=0.7\,162\,162\,162\,\ldots$

Здесь повторение равно 162, а длина повторения равна 3. Сначала мы умножаем на соответствующую степень 10, чтобы переместить десятичную точку вправо так, чтобы она находилась прямо перед повторением. В этом примере мы умножим на 10, чтобы получить:

$10A=7.162\,162\,162\,\ldots$

Теперь умножим это уравнение на 10. ^р где r — длина повтора. Это приводит к перемещению десятичной точки перед «следующим» повторением. В нашем примере умножьте на 10. ³ :

$10,000A=7\,162.162\,162\,\ldots$

Результат двух умножений дает два разных выражения с одинаковой «десятичной частью», то есть хвостовой конец 10 000 А соответствует хвостовому концу 10 А. точно Здесь и 10 000 А , и 10 А имеют 0,162 162 162 ... после запятой.

Следовательно, когда мы вычитаем уравнение 10 А из уравнения 10 000 А , последний конец 10 А компенсирует хвостовой конец 10 000 А, оставляя нас:

$9990A=7155.$

Затем

$A={\frac {7155}{9990}}={\frac {53}{74}}$

представляет собой отношение целых чисел и, следовательно, является рациональным числом.

Иррациональные силы

Дов Жарден дал простое неконструктивное доказательство того, что существуют два иррациональных числа a и b такие, что a ^б рационально:

Рассмотрим √ 2 ^{√ 2} ; если это рационально, то возьмем a = b = √ 2 . В противном случае примите за иррациональное число √ 2. ^{√ 2} и б знак равно √ 2 . Тогда ​ ^б = ( √ 2 ^{√ 2} ) ^{√ 2} = √ 2 ^{√ 2 · √ 2} = √ 2 ² = 2, что рационально.

Хотя приведенный выше аргумент не делает выбора между этими двумя случаями, теорема Гельфонда–Шнайдера показывает, что √ 2 ^{√ 2} трансцендентально и , следовательно, иррационально. Эта теорема утверждает, что если a и b являются алгебраическими числами , a не равно 0 или 1, а b не является рациональным числом, то любое значение a ^б может быть более одного значения в степень комплексного числа — трансцендентное число (при возведении ).

Пример, который обеспечивает простое конструктивное доказательство:

$\left({\sqrt {2}}\right)^{\log _{\sqrt {2}}3}=3.$

Основание левой части иррационально, а правая часть рациональна, поэтому необходимо доказать, что показатель степени в левой части $\log _{\sqrt {2}}3$, иррационально. Это происходит потому, что по формуле, связывающей логарифмы с разными основаниями,

$\log _{\sqrt {2}}3={\frac {\log _{2}3}{\log _{2}{\sqrt {2}}}}={\frac {\log _{2}3}{1/2}}=2\log _{2}3$

который мы можем предположить, ради установления противоречия , равным отношению m/n натуральных чисел. Затем $\log _{2}3=m/2n$ следовательно $2^{\log _{2}3}=2^{m/2n}$ следовательно $3=2^{m/2n}$ следовательно $3^{2n}=2^{m}$, что является противоречивой парой простых факторизаций и, следовательно, нарушает фундаментальную теорему арифметики (единственная простая факторизация).

Более сильный результат следующий: Каждое рациональное число в интервале $((1/e)^{1/e},\infty )$ можно записать либо как ^а для некоторого иррационального числа a или n ^н для некоторого натурального числа n . Сходным образом, каждое положительное рациональное число можно записать либо как $a^{a^{a}}$ для некоторого иррационального числа a или as $n^{n^{n}}$ для некоторого натурального числа n .

Открытые вопросы

Неизвестно, если $\pi +e$ (или $\pi -e$) иррационально. На самом деле не существует пары ненулевых целых чисел $m,n$ для которого известно, $m\pi +ne$ иррационально. Более того, неизвестно, будет ли множество $\{\pi ,e\}$ независима алгебраически над $\mathbb {Q}$.

Неизвестно, если $\pi e,\ \pi /e,\ \pi ^{e},\ \pi ^{\sqrt {2}},\ \ln \pi ,$ Константа Каталана , или постоянная Эйлера-Машерони. $\gamma$ иррациональны. Неизвестно, является ли какая-либо из тетраций $^{n}\pi$ или $^{n}e$ рационально для некоторого целого числа $n>1.$

В конструктивной математике

В конструктивной математике исключенное среднее недействительно, поэтому неверно, что каждое действительное число является рациональным или иррациональным. Таким образом, понятие иррационального числа распадается на множество различных понятий. Можно принять традиционное определение иррационального числа как действительного числа, которое не является рациональным. Однако существует второе определение иррационального числа, используемое в конструктивной математике: действительное число $r$ является иррациональным числом, если оно отделено от каждого рационального числа, или, что то же самое, если расстояние $\vert r-q\vert$ между $r$ и каждое рациональное число $q$ является положительным. Это определение сильнее традиционного определения иррационального числа. Это второе определение используется в доказательстве Эррета Бишопа , что квадратный корень из 2 иррационален .

Набор всех иррациональных

Поскольку реалы образуют несчетное число подмножеством которого являются рациональные числа множество, счетным , дополнительное множествоиррациональное неисчислимо.

При обычной ( евклидовой ) функции расстояния $d(x,y)=\vert x-y\vert$действительные числа являются метрическим пространством и, следовательно, также топологическим пространством . Ограничение функции евклидова расстояния придает иррациональным числам структуру метрического пространства. Поскольку подпространство иррациональных чисел не замкнуто,индуцированная метрика не является полной . Будучи G-дельта-множеством — т. е. счетным пересечением открытых подмножеств — в полном метрическом пространстве, пространство иррациональных чисел полностью метризуемо : то есть существует метрика на иррациональные числа, индуцирующая ту же топологию, что и ограничение евклидова числа. метрика, но относительно которой иррациональные числа полны. Это можно увидеть, не зная вышеупомянутого факта о G-дельта-множествах: разложение иррационального числа в цепную дробь определяет гомеоморфизм из пространства иррациональных чисел в пространство всех последовательностей натуральных чисел, которое, как легко видеть, полностью метризуемо.

Более того, множество всех иррациональных чисел представляет собой несвязное метризуемое пространство. Фактически, иррациональные числа, наделенные топологией подпространства, имеют базис из замкнуто-замкнутых групп, поэтому пространство нульмерно .

См. также

• Номер Брюно
• Вычислимое число
• Диофантово приближение
• Доказательство того, что e иррационально
• Доказательство того, что π иррационально
• Квадратный корень из 3
• Квадратный корень из 5
• Тригонометрическое число

Системы счисления Сложный $:\;\mathbb {C}$ Настоящий $:\;\mathbb {R}$ Рациональный $:\;\mathbb {Q}$ Целое число $:\;\mathbb {Z}$ Естественный $:\;\mathbb {N}$ Ноль : 0 Один : 1 Простые числа Составные числа Отрицательные целые числа Фракция Конечная десятичная дробь Диадический (конечный бинарный) Повторяющаяся десятичная дробь иррациональный Алгебраическая иррациональность трансцендентный Воображаемый

Дальнейшее чтение

• Адриен-Мари Лежандр , Элементы геометрии , Примечание IV, (1802), Париж
• Рольф Валлиссер, «О доказательстве Ламбертом иррациональности числа π», в книге «Алгебраическая теория чисел и диофантовый анализ» , Франц Хальтер-Кох и Роберт Ф. Тичи, (2000), Вальтер де Грюйтер

Внешние ссылки

• Парадоксы и несоизмеримость Зенона. Архивировано 13 мая 2016 г. в Wayback Machine (nd). Проверено 1 апреля 2008 г.