Квадратный корень из 3

Квадратный корень из 3
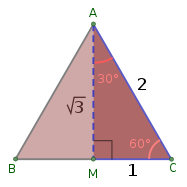
	Высота равностороннего треугольника со сторонами длиной 2 равна квадратному корню из 3.
Представительства
десятичный	1.73205 08075 68877 2935...
Непрерывная дробь

Квадратный корень из 3 — это положительное действительное число , которое при умножении само на себя дает число 3 . Математически это обозначается как ${\textstyle {\sqrt {3}}}$ или $3^{1/2}$ . Точнее, его называют главным квадратным корнем из 3, чтобы отличить его от отрицательного числа с тем же свойством. Квадратный корень из 3 — иррациональное число . Она также известна как константа Теодора , в честь Феодора Кириненского , который доказал ее иррациональность. ^{[ нужна ссылка ]}

В 2013 году его числовое значение в десятичной системе счисления было рассчитано до десяти миллиардов цифр. ^[1] Его десятичное расширение , записанное здесь до 65 десятичных знаков, дано OEIS : A002194 :

1.73205 08075 68877 29352 74463 41505 87236 69428 05253 81038 06280 55806

Фракция ${\textstyle {\frac {97}{56}}}$ ( 1,732 142 857 ...) можно использовать как хорошее приближение. Несмотря на то, что знаменатель равен всего 56, оно отличается от правильного значения менее чем на ${\textstyle {\frac {1}{10,000}}}$ (примерно ${\textstyle 9.2\times 10^{-5}}$ с относительной ошибкой ${\textstyle 5\times 10^{-5}}$ ). Округленное значение 1,732 соответствует реальному значению с точностью до 0,01%. ^{[ нужна ссылка ]}

Фракция ${\textstyle {\frac {716,035}{413,403}}}$ ( 1,732 050 807 56 ...) с точностью до ${\textstyle 1\times 10^{-11}}$ . ^{[ нужна ссылка ]}

Архимед сообщил диапазон его значений: ${\textstyle ({\frac {1351}{780}})^{2}>3>({\frac {265}{153}})^{2}}$ . ^[2]

Нижний предел ${\textstyle {\frac {1351}{780}}}$ является точным приближением для ${\sqrt {3}}$ к ${\textstyle {\frac {1}{608,400}}}$ (шесть десятичных знаков, относительная погрешность ${\textstyle 3\times 10^{-7}}$ ) и верхний предел ${\textstyle {\frac {265}{153}}}$ к ${\textstyle {\frac {2}{23,409}}}$ (четыре знака после запятой, относительная погрешность ${\textstyle 1\times 10^{-5}}$ ).

Выражения [ править ]

Ее можно выразить как непрерывную дробь [1; 1, 2, 1, 2, 1, 2, 1, …] (последовательность A040001 в OEIS ).

Так что верно сказать:

{\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}

тогда когда $n\to \infty$ :

{\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1

Его также можно выразить с помощью обобщенных цепных дробей, таких как

[2;-4,-4,-4,...]=2-{\cfrac {1}{4-{\cfrac {1}{4-{\cfrac {1}{4-\ddots }}}}}}

что есть [1; 1, 2, 1, 2, 1, 2, 1, …] оценивается на каждом втором семестре.

Геометрия и тригонометрия [ править ]

Высота длиной с равностороннего треугольника ребра 2 равна √ 3 . А также длинный катет треугольника 30-60-90 с гипотенузой 2.

А, высота правильного шестиугольника со стороной длиной 1.

Квадратный корень из 3 можно найти как длину катета равностороннего треугольника, охватывающего круг диаметром 1.

Если равносторонний треугольник прямоугольного треугольника со сторонами длиной 1 разрезать на две равные половины, разделив внутренний угол пополам, чтобы получился прямой угол с одной стороной, гипотенуза будет равна длине один, а стороны будут иметь длину ${\textstyle {\frac {1}{2}}}$ и ${\textstyle {\frac {\sqrt {3}}{2}}}$ . Из этого, ${\textstyle \tan {60^{\circ }}={\sqrt {3}}}$ , ${\textstyle \sin {60^{\circ }}={\frac {\sqrt {3}}{2}}}$ , и ${\textstyle \cos {30^{\circ }}={\frac {\sqrt {3}}{2}}}$ .

Квадратный корень из 3 также появляется в алгебраических выражениях для различных других тригонометрических констант , включая ^[3] синусы 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84° и 87. °.

Это расстояние между параллельными сторонами правильного шестиугольника со сторонами длиной 1.

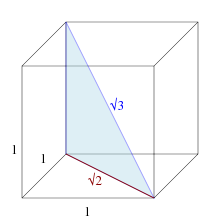
Это длина пространственной диагонали единичного куба .

vesica piscis имеет соотношение большой оси к малой оси, равное $1:{\sqrt {3}}$ . Это можно показать, построив внутри него два равносторонних треугольника.

Другое возникновение использование и

Энергетика [ править ]

В энергетике напряжение между двумя фазами в трехфазной системе равно ${\textstyle {\sqrt {3}}}$ раз напряжение между линией и нейтралью. Это связано с тем, что любые две фазы расположены на расстоянии 120° друг от друга, а две точки на окружности, находящиеся на расстоянии 120° друг от друга, разделены расстоянием ${\textstyle {\sqrt {3}}}$ раз больше радиуса (см. примеры геометрии выше). ^{[ нужна ссылка ]}

Специальные функции [ править ]

Известно, что большинство корней n- й производной $J_{\nu }^{(n)}(x)$ (где n < 18 и $J_{\nu }(x)$ — функция Бесселя первого рода порядка $\nu$ ) трансцендентны . Исключение составляют только числа $\pm {\sqrt {3}}$ , которые являются алгебраическими корнями обоих $J_{1}^{(3)}(x)$ и $J_{0}^{(4)}(x)$ . ^[4]^{[ нужны разъяснения ]}