Травяной додекаэдр

Травяной додекаэдр
Травяной додекаэдр
Тип	Параллелоэдр ; Многогранник, заполняющий пространство ; Зоноэдр
Лица	12
Края	24
Вершины	14
Группа симметрии	Д 2 часа
Характеристики	выпуклый

В геометрии додекаэдр Билинского представляет собой выпуклый многогранник с двенадцатью равными золотого ромба гранями . Он имеет ту же топологию, но другую геометрию, чем гране-транзитивный ромбический додекаэдр . Это параллелоэдр .

История

Эта форма появляется в книге Джона Лоджа Коули 1752 года , названной додекаромбом . ^[1]^[2] Он назван в честь Станко Билински , который заново открыл его в 1960 году. ^[3] Сам Билинский называл его ромбдодекаэдром второго рода . ^[4] Открытие Билинского исправило упущение 75-летней давности в Евграфа Федорова классификации выпуклых многогранников с конгруэнтными ромбическими гранями. ^[5]

Определение и свойства

Определение

Додекаэдр Билинского образуется путем склеивания двенадцати равных золотых ромбов . Это ромбы , диагонали которых находятся в золотом сечении :

\varphi ={{1+{\sqrt {5}}} \over 2}\approx 1.618~034.

График полученного многогранника изоморфен графику ромбододекаэдра , но грани ориентированы по-разному: у одной пары противоположных ромбов длинная и короткая диагонали перевернуты, относительно ориентации соответствующих ромбов в ромдодекаэдре.

Симметрия

Из-за своего переворота додекаэдр Билинского имеет более низкий порядок симметрии; его группа симметрии — это группа прямоугольного кубоида : $D 2h, [2,2], (*222)$ порядка 8. Это подгруппа октаэдрической симметрии ; его элементами являются три оси симметрии 2-го порядка, три плоскости симметрии (которые также являются осевыми плоскостями этого твердого тела) и центр инверсионной симметрии . Группа вращения додекаэдра Билинского равна $D 2, [2,2] +, (222),$ порядка 4.

Вершины

Как и ромбический додекаэдр, додекаэдр Билинского имеет восемь вершин степени 3 и шесть вершин степени 4. Он имеет две вершины на вертикальной оси и четыре вершины на каждой осевой плоскости. Но из-за переворота его невершинные вершины образуют два квадрата (красный и зеленый) и один прямоугольник (синий), а всего его четырнадцать вершин относятся к четырем разным видам:

две вершины 4-й степени, окруженные четырьмя острыми гранями (вершины вертикальной оси, черные на первом рисунке);
четыре вершины 4-й степени, окруженные тремя острыми и одним тупым гранями (вершины горизонтально-осевой плоскости, синие на первом рисунке);
четыре вершины степени 3, окруженные тремя тупыми гранями (одна вершина в вертикальной осевой плоскости, красная на первом рисунке);
четыре вершины степени 3, окруженные двумя тупыми и одним острым гранями (остальные вершины в вертикально-осевой плоскости, зеленые на первом рисунке).

Лица

Дополнительные внутренние углы золотого ромба: ^[6]

острый угол:

\alpha =\arctan 2\approx 63.434~949^{\circ };

тупой угол:

\beta =\pi -\arctan 2\approx 116.565~051^{\circ }.

Грани додекаэдра Билинского представляют собой двенадцать равных золотых ромбов; но из-за реверса они бывают трех разных видов:

восемь апикальных граней со всеми четырьмя видами вершин,
две боковые грани с чередующимися синими и красными вершинами (спереди и сзади на первом рисунке),
две боковые грани с чередующимися синими и зелеными вершинами (слева и справа на первом рисунке).

(См. также рисунок с окрашенными краями и передними гранями.)

Края

24 ребра додекаэдра Билинского имеют одинаковую длину; но из-за реверса они бывают четырех разных видов:

четыре апикальных ребра с черными и красными вершинами (на первом рисунке),
четыре апикальных ребра с черными и зелеными вершинами (на первом рисунке),
восемь боковых ребер с синими и красными вершинами (на первом рисунке),
восемь боковых ребер с синими и зелеными вершинами (на первом рисунке).

(См. также рисунок с окрашенными краями и передними гранями.)

Декартовы координаты

Вершины додекаэдра Билинского толщиной 2 имеют следующие декартовы координаты , где $φ$ — золотое сечение :

степень	цвет	координаты
3	красный	( $0, \pm1, \pm1$ )
3	зеленый	( $\pm φ, 0, \pm φ$ )
4	синий	( $\pm φ, \pm1, 0$ )
4	черный	( $0, 0, \pm φ 2$ )
Красные/зеленые/синие вершины лежат в плоскости, перпендикулярной оси того же цвета.

другие объекты недвижимости
The Bilinski dodecahedron of this size has: length of longest body diagonal (i.e. lying on opposite black degree-4 vertices): $2~\varphi ^{2}=3+{\sqrt {5}}\approx 5.236~068;$ length of shorter body diagonals (i.e. lying on opposite blue degree-4 vertices): $2{\sqrt {2+\varphi }}={\sqrt {2\left(5+{\sqrt {5}}\right)}}\approx 3.804~226;$ edge length: ${\sqrt {2+\varphi }}={\sqrt {\frac {5+{\sqrt {5}}}{2}}}\approx 1.902~113.$

В семействах многогранников

Додекаэдр Билинского — параллелоэдр ; таким образом, это также заполняющий пространство многогранник и зоноэдр .

Связь с ромбическим додекаэдром

В статье 1962 года Х.С.М. Коксетер утверждал, что додекаэдр Билинского можно получить путем аффинного преобразования из ромбического додекаэдра, но это неверно. ^[7]

В ромбододекаэдре: каждая длинная диагональ тела (т. е. лежащая в вершинах противоположной степени 4) параллельна коротким диагоналям четырех граней.

В додекаэдре Билинского: самая длинная диагональ тела (т. е. лежащая в противоположных черных вершинах степени 4) параллельна коротким диагоналям двух граней и длинным диагоналям двух других граней; более короткие диагонали тела (т.е. лежащие в противоположных синих вершинах степени 4) не параллельны диагонали какой-либо грани. ^[5]

При любом аффинном преобразовании ромбододекаэдра: каждая длинная диагональ тела (т. е. лежащая в вершинах противоположной степени 4) остается параллельной четырем диагоналям граней, и они остаются одинаковой (новой) длины.

Зоноэдры с золотыми ромбическими гранями.

Додекаэдр Билинского можно образовать из ромботриаконтаэдра (еще одного зоноэдра с тридцатью конгруэнтными золотыми ромбическими гранями) путем удаления или схлопывания двух зон или поясов из десяти и восьми золотых ромбических граней с параллельными краями. Удаление только одной зоны из десяти граней дает ромбический икосаэдр . Удаление трех зон из десяти, восьми и шести граней дает золотой ромбоэдр . ^[4]^[5] Таким образом, удаление зоны из шести граней из додекаэдра Билинского дает золотой ромбоэдр. Додекаэдр Билинского можно разрезать на четыре золотых ромбоэдра, по два каждого типа. ^[8]

Вершины зоноэдров с золотыми ромбическими гранями можно вычислить с помощью линейных комбинаций от двух до шести порождающих векторов ребер с коэффициентами 0 или 1. ^[9] Ремень n $m n$ означает пояс, представляющий $векторов направления$ и содержащий $m$ сопараллельных ребер одинаковой длины. Додекаэдр Билинского имеет четыре пояса по шесть сопараллельных ребер.

Эти зоноэдры представляют собой проекционные оболочки гиперкубов с n $-$ мерным проекционным базисом и золотым сечением ( $φ$ ). Для $n = 6$ конкретный базис:

х = (1, φ, 0,-1, φ, 0),

у = (φ, 0, 1, φ, 0,-1),

z = (0, 1, φ, 0,-1, φ).

При $n = 5$ базис тот же, но шестой столбец удален. При $n = 4$ удаляются пятый и шестой столбцы.

Зоноэдры с золотыми ромбическими гранями.
Солидное имя	Триаконтаэдр	Икосаэдр	Додекаэдр	Шестигранник (острый/тупой)	Ромб (двусторонний)
Полный симметрия	I _h (заказ 120)	Д _5д (заказ 20)	Д _{2 часа} (заказ 8)	Д _3д (заказ 12)	Д _{2 часа} (заказ 8)
n поясов из (2( n −1)) _n // ребер ^[10]	6 ремней 10 ₆ // ребра	5 поясов 8 ₅ // края	4 ремня из 6 ₄ // края	3 ремня из 4 ₃ // края	2 ремня из 2 ₂ // края
n ( n −1) Грани ^[11]	30	20 (−10)	12 (−8)	6 (−6)	2 (−4)
2 n ( n −1) Ребра ^[12]	60	40 (−20)	24 (−16)	12 (−12)	4 (−8)
n ( n −1)+2 вершины ^[13]	32	22 (−10)	14 (−8)	8 (−6)	4 (−4)
Сплошное изображение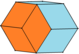
Изображение с параллельными краями
Диссекция	10 + 10	5 + 5	2 + 2
Проективный n- куб	6-куб.	5-куб	4-кубовый	3-куб	2-куб.
Проективный n- кубическое изображение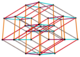

Ссылки

^ Харт, Джордж В. (2000), «Рассечение ромбического эннеаконтаэдра по цвету» , Symmetry: Culture and Science , 11 (1–4): 183–199, MR 2001417 .
^ Коули, Джон Лодж (1752), «Геометрия стала проще»; Или «Новое методическое объяснение элементов геометрии» , Лондон, лист 5, рис. 16 . Цитируется Хартом (2000) .
^ Билински, С. (1960), "Über die Rhombenisoder", Glasnik Mat. Физический. Астр. , 15 : 251–263, Збл 0099.15506 .
↑ Перейти обратно: Перейти обратно: ^а ^б Кромвель, Питер Р. (1997), Многогранники: одна из самых очаровательных глав геометрии , Кембридж: Издательство Кембриджского университета , стр. 156, ISBN 0-521-55432-2 , МР 1458063 .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Грюнбаум, Бранко (2010), «Додекаэдр Билинского и различные параллелоэдры, зоноэдры, моноэдры, изозоноэдры и другие эдры», The Mathematical Intelligencer , 32 (4): 5–15, doi : 10.1007/s00283-010-9138-7 , hdl : 1773/15593 , MR 2747698 , S2CID 120403108 .
^ Огава, Тору (январь 1987 г.), «Симметрия трехмерных квазикристаллов», Materials Science Forum , 22–24: 187–200, doi : 10.4028/www.scientific.net/msf.22-24.187 , S2CID 137677876 . См., в частности, таблицу 1, с. 188.
^ Коксетер, HSM (1962), «Классификация зоноэдров с помощью проективных диаграмм», Journal de Mathématiques Pures et Appliquées , 41 : 137–156, MR 0141004 . Перепечатано в Коксетер, HSM (1968), Двенадцать геометрических эссе , Карбондейл, Иллинойс: Издательство Южного Иллинойского университета , MR 0310745 ( Красота геометрии. Двенадцать эссе , Дувр, 1999, MR) 1717154 ).
^ «Золотые ромбоэдры» , CutOutFoldUp , получено 26 мая 2016 г.
^ Пусть V обозначает количество вершин, а e _k обозначает k -й образующий вектор ребра, где 1 ≤ k ≤ n ;
для 2 ≤ n ≤ 3, V = card(𝒫 { e ₁ ,..., e _n }) = 2 ^н;
для 4 ≤ n ≤ 6, V < 2 ^н, поскольку некоторые из линейных комбинаций из четырех-шести порождающих векторов ребер с коэффициентами 0 или 1 заканчиваются строго внутри золотого ромбического зоноэдра.
^ Пусть e _k обозначает k -й образующий вектор ребра, где 1 ≤ k ≤ n ;
пример: e ₁ и en _{соответствуют} соответствуют паре противоположных ромбов, ..., n _{−1 и} en e _другой паре противоположных ромбов; всего: e _n представлено в n −1 различных парах противоположных ромбов, то есть в 2( n −1) разных ромбах; они образуют полосу; это закрыто, иначе оно было бы бесконечным; поэтому e _n представлено в 2( n −1) различных (копараллельных) ребрах этого пояса.
^ В золотом ромбическом зоноэдре каждая пара противоположных ромбов соответствует двум из n образующих векторов ребер, поэтому он имеет:
F = 2×( ^н₂ ) = n ( n −1) граней.
^ У золотого ромбического зоноэдра каждая грань лежит на четырех гранях, а каждое ребро лежит на двух гранях, поэтому он имеет:
E = 4 F /2 = 2 F = 2 n ( n −1) ребер.
^ Золотой ромбический зоноэдр имеет:
V = E − F +2 = 2 n ( n −1) − n ( n −1)+2 = n ( n −1)+2 вершины.

Внешние ссылки

VRML Модель , Джордж Харт : www .Джорджхарт .с /виртуальные-многогранники /врмл /ромбический _додекаэдр _из _второй _добрый .wrl
анимация и координаты, Дэвид И. МакКуи: dmccooey .с /многогранники /БилинскиДодекаэдр .html
Новый ромбдодекаэдр из Хорватии! , видео на YouTube Мэтта Паркера

[1] Харт, Джордж В. (2000), «Рассечение ромбического эннеаконтаэдра по цвету» , Symmetry: Culture and Science , 11 (1–4): 183–199, MR 2001417 .

[2] Коули, Джон Лодж (1752), «Геометрия стала проще»; Или «Новое методическое объяснение элементов геометрии» , Лондон, лист 5, рис. 16 . Цитируется Хартом (2000) .

[3] Билински, С. (1960), "Über die Rhombenisoder", Glasnik Mat. Физический. Астр. , 15 : 251–263, Збл 0099.15506 .

[crom-4] Перейти обратно: Перейти обратно: ^а ^б Кромвель, Питер Р. (1997), Многогранники: одна из самых очаровательных глав геометрии , Кембридж: Издательство Кембриджского университета , стр. 156, ISBN 0-521-55432-2 , МР 1458063 .

[grun-5] Перейти обратно: Перейти обратно: ^а ^б ^с Грюнбаум, Бранко (2010), «Додекаэдр Билинского и различные параллелоэдры, зоноэдры, моноэдры, изозоноэдры и другие эдры», The Mathematical Intelligencer , 32 (4): 5–15, doi : 10.1007/s00283-010-9138-7 , hdl : 1773/15593 , MR 2747698 , S2CID 120403108 .

[ogawa-6] Огава, Тору (январь 1987 г.), «Симметрия трехмерных квазикристаллов», Materials Science Forum , 22–24: 187–200, doi : 10.4028/www.scientific.net/msf.22-24.187 , S2CID 137677876 . См., в частности, таблицу 1, с. 188.

[7] Коксетер, HSM (1962), «Классификация зоноэдров с помощью проективных диаграмм», Journal de Mathématiques Pures et Appliquées , 41 : 137–156, MR 0141004 . Перепечатано в Коксетер, HSM (1968), Двенадцать геометрических эссе , Карбондейл, Иллинойс: Издательство Южного Иллинойского университета , MR 0310745 ( Красота геометрии. Двенадцать эссе , Дувр, 1999, MR) 1717154 ).

[8] «Золотые ромбоэдры» , CutOutFoldUp , получено 26 мая 2016 г.

[9] Пусть V обозначает количество вершин, а e _k обозначает k -й образующий вектор ребра, где 1 ≤ k ≤ n ;
для 2 ≤ n ≤ 3, V = card(𝒫 { e ₁ ,..., e _n }) = 2 ^н;
для 4 ≤ n ≤ 6, V < 2 ^н, поскольку некоторые из линейных комбинаций из четырех-шести порождающих векторов ребер с коэффициентами 0 или 1 заканчиваются строго внутри золотого ромбического зоноэдра.

[10] Пусть e _k обозначает k -й образующий вектор ребра, где 1 ≤ k ≤ n ;
пример: e ₁ и en _{соответствуют} соответствуют паре противоположных ромбов, ..., n _{−1 и} en e _другой паре противоположных ромбов; всего: e _n представлено в n −1 различных парах противоположных ромбов, то есть в 2( n −1) разных ромбах; они образуют полосу; это закрыто, иначе оно было бы бесконечным; поэтому e _n представлено в 2( n −1) различных (копараллельных) ребрах этого пояса.

[11] В золотом ромбическом зоноэдре каждая пара противоположных ромбов соответствует двум из n образующих векторов ребер, поэтому он имеет:
F = 2×( ^н₂ ) = n ( n −1) граней.

[12] У золотого ромбического зоноэдра каждая грань лежит на четырех гранях, а каждое ребро лежит на двух гранях, поэтому он имеет:
E = 4 F /2 = 2 F = 2 n ( n −1) ребер.

[13] Золотой ромбический зоноэдр имеет:
V = E − F +2 = 2 n ( n −1) − n ( n −1)+2 = n ( n −1)+2 вершины.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]