Ромбический икосаэдр
| Ромбический икосаэдр | |
|---|---|
 | |
| Тип | Зоноэдр |
| Лица | соответствуют 20 золотых ромбов |
| Края | 40 |
| Вершины | 22 |
| Группа симметрии | Д 5д = Д 5в , [2 + ,10], (2*5) |
| Двойной многогранник | с неправильной гранью пятиугольный гиробикупол |
| Характеристики | выпуклый |

Ромбический икосаэдр представляет собой многогранник , имеющий форму сплюснутой сферы . Его 20 граней представляют собой конгруэнтные золотые ромбы; [1] В каждой вершине сходятся 3, 4 или 5 граней. У него пять граней (зеленые на верхнем рисунке), сходящихся на каждом из двух полюсов; эти две вершины лежат на его оси 5-кратной симметрии, которая перпендикулярна 5 осям 2-кратной симметрии, проходящим через середины противоположных экваториальных ребер (пример на верхнем рисунке: самые левые и самые правые средние ребра) . Остальные 10 его граней следуют по экватору: 5 над ним и 5 под ним; У каждого из этих 10 ромбов 2 из 4 сторон лежат на зигзагообразном косом экваторе десятиугольника . Ромбический икосаэдр имеет 22 вершины. Он имеет D 5 d , [2 + ,10], (2*5) группа симметрии порядка 20; таким образом, у него есть центр симметрии (поскольку 5 нечетно).
Несмотря на то, что все его грани конгруэнтны, ромбический икосаэдр не является транзитивным по граням , поскольку можно отличить, находится ли конкретная грань вблизи экватора или вблизи полюса, исследуя типы вершин, окружающих эту грань.
Зоноэдр
[ редактировать ]Ромбический икосаэдр представляет собой зоноэдр , двойственный пятиугольному гиробикуполу с правильными треугольными, правильными пятиугольными и неправильными четырехугольными гранями.
Ромбический икосаэдр имеет 5 наборов по 8 параллельных ребер, называемых 8 5 поясами .
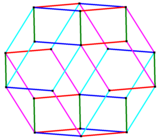 | Ребра ромбического икосаэдра можно сгруппировать в 5 параллельных наборов, как показано на этой каркасной ортогональной проекции. |
Ромбический икосаэдр образует выпуклую оболочку проекции пятимерного куба с вершиной вперед в трех измерениях. 32 вершины 5-куба отображаются в 22 внешние вершины ромбического икосаэдра, а оставшиеся 10 внутренних вершин образуют пятиугольную антипризму .
Точно так же можно получить додекаэдр Билинского из 4-куба , а — ромбический триаконтаэдр из 6-куба .
Связанные многогранники
[ редактировать ]Ромбический икосаэдр можно получить из ромботриаконтаэдра, удалив пояс из 10 средних граней.
 Ромбический триаконтаэдр можно рассматривать как вытянутый ромбический икосаэдр. | 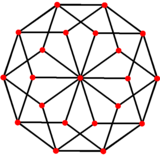 Ромбический икосаэдр и ромбический триаконтаэдр имеют одинаковую 10-кратную симметричную ортогональную проекцию. (*) |
(*) (Например, на левом рисунке):
Ортогональная проекция (вертикального) пояса из 10 средних граней ромботриаконтаэдра представляет собой всего лишь (горизонтальный) внешний правильный десятиугольник общей ортогональной проекции.
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «Ромбический икосаэдр» . mathworld.wolfram.com . Проверено 20 декабря 2019 г.