Распределение вероятностей

Чтобы узнать о других целях, см. Распространение .

В теории вероятностей и статистике распределение вероятностей — это математическая функция которая определяет вероятности возникновения различных возможных результатов эксперимента , . Это математическое описание случайного явления с точки зрения его выборочного пространства и вероятностей событий . ( подмножеств выборочного пространства)

Например, если X используется для обозначения результата подбрасывания монеты («эксперимент»), то распределение вероятностей X примет значение 0,5 (1 к 2 или 1/2) для X = орла и 0,5 для X = решка (при условии, что монета честная ). Чаще всего распределения вероятностей используются для сравнения относительного появления множества различных случайных величин.

Распределения вероятностей могут быть определены по-разному: для дискретных или для непрерывных переменных. Дистрибутивам со специальными свойствами или для особо важных приложений присваиваются особые имена.

Введение

Распределение вероятностей — это математическое описание вероятностей событий, подмножеств выборочного пространства . Пространство выборки, часто представленное в обозначениях $\ \Omega \ ,$– множество всех возможных исходов наблюдаемого случайного явления; это может быть любой набор: набор действительных чисел , набор описательных меток, набор векторов , набор произвольных нечисловых значений и т. д. Например, пространство выборки при подбрасывании монеты будет Ω = { " орел», «решка» } .

Чтобы определить распределения вероятностей для конкретного случая случайных величин (чтобы выборочное пространство можно было рассматривать как числовой набор), принято различать дискретные и абсолютно непрерывные случайные величины . В дискретном случае достаточно задать функцию массы вероятности $\ p\$ присвоение вероятности каждому возможному исходу: например, при бросании игральной кости каждая из шести цифр от «1» до «6» , соответствующих количеству точек на игральной кости, имеет вероятность $\ {\tfrac {1}{6}}~.$Затем вероятность события определяется как сумма вероятностей всех исходов, удовлетворяющих событию; например, вероятность события «на кубике выпадет четное значение» равна

$$\ p({\text{“}}2{\text{”}})+p({\text{“}}4{\text{”}})+p({\text{“}}6{\text{”}})={\tfrac {1}{6}}+{\tfrac {1}{6}}+{\tfrac {1}{6}}={\tfrac {1}{2}}~.$$

Напротив, когда случайная величина принимает значения из континуума, тогда по соглашению любому отдельному результату присваивается вероятность, равная нулю. Для таких непрерывных случайных величин только события, которые включают в себя бесконечное количество результатов, таких как интервалы, имеют вероятность больше 0.

Например, рассмотрим измерение веса куска ветчины в супермаркете и предположим, что весы могут обеспечить сколь угодно много цифр точности. Тогда вероятность того, что он весит ровно 500 г, должна быть равна нулю, поскольку независимо от того, насколько высок выбранный уровень точности, нельзя предполагать, что в оставшихся пропущенных цифрах, игнорируемых уровнем точности, нет ненулевых десятичных цифр.

Однако для того же варианта использования можно выполнить требования контроля качества, например, что упаковка ветчины «500 г» должна весить от 490 г до 510 г с вероятностью не менее 98%. Это возможно, поскольку это измерение не требует такой высокой точности от основного оборудования.

Рисунок 1: Левый график показывает функцию плотности вероятности. На правом графике показана кумулятивная функция распределения, для которой значение a равно площади под кривой плотности вероятности слева от a .

Абсолютно непрерывные распределения вероятностей можно описать несколькими способами. Функция плотности вероятности описывает бесконечно малую вероятность любого заданного значения, а вероятность того, что результат лежит в заданном интервале, может быть вычислена путем интегрирования функции плотности вероятности по этому интервалу. Альтернативное описание распределения осуществляется с помощью кумулятивной функции распределения , которая описывает вероятность того, что случайная величина не больше заданного значения (т. е. $\ {\boldsymbol {\mathcal {P}}}(X<x)\$ для некоторых $\ x\$). Кумулятивная функция распределения представляет собой площадь под функцией плотности вероятности из $\ -\infty \$ к $\ x\ ,$ как показано на рисунке 1.

вероятности

Распределение вероятностей можно описать в различных формах, например, с помощью функции массы вероятности или кумулятивной функции распределения. Одно из наиболее общих описаний, применимое к абсолютно непрерывным и дискретным переменным, осуществляется с помощью функции вероятности. $P\colon {\mathcal {A}}\to \mathbb {R}$ чье входное пространство ${\mathcal {A}}$ является σ-алгеброй и на выходе дает действительного числа вероятность , в частности, число в $[0,1]\subseteq \mathbb {R}$.

Функция вероятности $P$ может принимать в качестве аргумента подмножества самого пространства выборки, как в примере с подбрасыванием монеты, где функция $P$было определено так, что P (орёл) = 0,5 и P (решка) = 0,5 . Однако из-за широкого использования случайных величин , которые преобразуют выборочное пространство в набор чисел (например, $\mathbb {R}$, $\mathbb {N}$), чаще изучаются распределения вероятностей, аргументами которых являются подмножества этих конкретных видов множеств (множеств чисел), и все распределения вероятностей, обсуждаемые в этой статье, относятся к этому типу. Обычно обозначают как $P(X\in E)$ вероятность того, что определенное значение переменной $X$ принадлежит определенному событию $E$.

Приведенная выше функция вероятности характеризует распределение вероятностей только в том случае, если оно удовлетворяет всем аксиомам Колмогорова , то есть:

1. $P(X\in E)\geq 0\;\forall E\in {\mathcal {A}}$, поэтому вероятность неотрицательна
2. $P(X\in E)\leq 1\;\forall E\in {\mathcal {A}}$, поэтому никакая вероятность не превосходит $1$
3. $P(X\in \bigcup _{i}E_{i})=\sum _{i}P(X\in E_{i})$ для любого счетного непересекающегося семейства множеств $\{E_{i}\}$

Понятие функции вероятности становится более строгим, если определить ее как элемент вероятностного пространства. $(X,{\mathcal {A}},P)$, где $X$ это набор возможных результатов, ${\mathcal {A}}$ это набор всех подмножеств $E\subset X$ вероятность которого можно измерить, и $P$ — это функция вероятности или мера вероятности , которая присваивает вероятность каждому из этих измеримых подмножеств $E\in {\mathcal {A}}$.

Распределения вероятностей обычно относятся к одному из двух классов. Дискретное распределение вероятностей применимо к сценариям, в которых набор возможных результатов дискретен (например, подбрасывание монеты, бросок игральной кости), а вероятности кодируются дискретным списком вероятностей результатов; в этом случае дискретное распределение вероятностей известно как функция массы вероятности . С другой стороны, абсолютно непрерывные распределения вероятностей применимы к сценариям, в которых набор возможных результатов может принимать значения в непрерывном диапазоне (например, действительные числа), такие как температура в определенный день. В абсолютно непрерывном случае вероятности описываются функцией плотности вероятности , а распределение вероятностей по определению является интегралом функции плотности вероятности. Нормальное распределение — это часто встречающееся абсолютно непрерывное распределение вероятностей. Более сложные эксперименты, например эксперименты со случайными процессами, определяемыми в непрерывном времени , могут потребовать использования более общих вероятностных мер .

Распределение вероятностей, выборочное пространство которого является одномерным (например, действительные числа, список меток, упорядоченные метки или двоичные числа), называется одномерным , а распределение, выборочное пространство которого представляет собой векторное пространство размерности 2 или более, называется многомерным . Одномерное распределение дает вероятности того, что одна случайная величина принимает разные значения; многомерное распределение ( совместное распределение вероятностей ) дает вероятности случайного вектора — списка двух или более случайных величин — принимающих различные комбинации значений. Важные и часто встречающиеся одномерные распределения вероятностей включают биномиальное распределение , гипергеометрическое распределение и нормальное распределение . Часто встречающимся многомерным распределением является многомерное нормальное распределение .

Помимо функции вероятности, кумулятивная функция распределения, функция массы вероятности и функция плотности вероятности, производящая функция момента и характеристическая функция также служат для идентификации распределения вероятностей, поскольку они однозначно определяют лежащую в основе кумулятивную функцию распределения.

Рисунок 2: Функция плотности вероятности (pdf) нормального распределения , также называемая гауссовой или «гауссовой кривой», наиболее важного абсолютно непрерывного случайного распределения. Как отмечено на рисунке, вероятности интервалов значений соответствуют площади под кривой.

Терминология

Ниже перечислены некоторые ключевые понятия и термины, широко используемые в литературе по теме распределений вероятностей.

Основные термины

• Случайная переменная : принимает значения из выборочного пространства; вероятности описывают, какие значения и набор значений принимаются с большей вероятностью.
• Событие : набор возможных значений (результатов) случайной величины, происходящий с определенной вероятностью.
• Функция вероятности или мера вероятности : описывает вероятность $P(X\in E)$ что событие $E,$ имеет место.
• Кумулятивная функция распределения : функция, оценивающая вероятность того, что $X$ примет значение меньше или равное $x$ для случайной величины (только для действительных случайных величин).
• Квантильная функция : обратная кумулятивной функции распределения. дает $x$ такая, что с вероятностью $q$, $X$ не превысит $x$.

вероятностей

• Дискретное распределение вероятностей : для многих случайных величин с конечным или счетным числом значений.
• Функция массы вероятности ( pmf ): функция, которая дает вероятность того, что дискретная случайная величина равна некоторому значению.
• Распределение частот : таблица, в которой отображается частота различных результатов в выборке .
• Относительное распределение частот : распределение частот , при котором каждое значение было разделено (нормализовано) на количество результатов в выборке (т. е. размер выборки).
• Категориальное распределение : для дискретных случайных величин с конечным набором значений.

непрерывные

• Абсолютно непрерывное распределение вероятностей : для многих случайных величин с несчетным числом значений.
• Функция плотности вероятности ( pdf ) или плотность вероятности : функция, значение которой в любой заданной выборке (или точке) в выборочном пространстве (набор возможных значений, принимаемых случайной величиной) можно интерпретировать как обеспечивающую относительную вероятность того, что значение случайная величина будет равна этой выборке.

Связанные термины

• Поддержка : набор значений, которые могут быть приняты с ненулевой вероятностью (или плотностью вероятности в случае непрерывного распределения) случайной величиной. Для случайной величины $X$, его иногда обозначают как $R_{X}$.
• Хвост : области, близкие к границам случайной величины, если pmf или pdf в них относительно невелики. Обычно имеет вид $X>a$, $X<b$ или их союз.
• Голова : регион, где pmf или pdf относительно высоки. Обычно имеет вид $a<X<b$.
• Ожидаемое значение или среднее значение : средневзвешенное значение возможных значений с использованием их вероятностей в качестве весов; или его непрерывный аналог.
• Медиана : значение, при котором набор значений меньше медианы и набор значений больше медианы имеют вероятность не более половины.
• Режим : для дискретной случайной величины значение с наибольшей вероятностью; для абсолютно непрерывной случайной величины - место, в котором функция плотности вероятности имеет локальный пик.
• Квантиль : q-квантиль — это значение $x$ такой, что $P(X<x)=q$.
• Дисперсия : второй момент pmf или pdf относительно среднего значения; важная мера дисперсии распределения .
• Стандартное отклонение : квадратный корень дисперсии и, следовательно, еще одна мера дисперсии.
• Симметрия : свойство некоторых распределений, в которых часть распределения слева от определенного значения (обычно медианы) является зеркальным отражением части справа.
• Асимметрия : мера того, насколько pmf или pdf «наклоняется» в одну сторону от своего среднего значения. Третий стандартизированный момент распределения.
• Куртозис : мера «упитанности» хвостов pmf или pdf. Четвертый стандартизированный момент распределения.

распределения

В частном случае действительной случайной величины распределение вероятностей может быть эквивалентно представлено кумулятивной функцией распределения вместо вероятностной меры. Кумулятивная функция распределения случайной величины $X$ относительно распределения вероятностей $p$ определяется как

$$F(x)=P(X\leq x).$$

Кумулятивная функция распределения любой вещественной случайной величины обладает свойствами:

• $F(x)$ не убывает;
• $F(x)$ является непрерывным справа ;
• $0\leq F(x)\leq 1$;
• $\lim _{x\to -\infty }F(x)=0$ и $\lim _{x\to \infty }F(x)=1$; и
• $\Pr(a<X\leq b)=F(b)-F(a)$.

И наоборот, любая функция $F:\mathbb {R} \to \mathbb {R}$ которая удовлетворяет первым четырем свойствам, указанным выше, является кумулятивной функцией распределения некоторого распределения вероятностей действительных чисел.

Любое распределение вероятностей можно разложить как смесь дискретного , абсолютно непрерывного и сингулярного непрерывного распределений . и, таким образом, любая кумулятивная функция распределения допускает разложение в выпуклую сумму трех соответствующих кумулятивных функций распределения.

вероятностей

Основная статья: Функция массы вероятности

Рисунок 3: Функция массы вероятности (pmf) $p(S)$ задает распределение вероятностей для суммы $S$отсчетов от двух игральных костей . Например, на рисунке показано, что $p(11)=2/36=1/18$. PMF позволяет вычислять вероятности таких событий, как $P(X>9)=1/12+1/18+1/36=1/6$и все остальные вероятности в распределении.

Рисунок 4: Массовая функция вероятности дискретного распределения вероятностей. Вероятности одиночных элементов {1}, {3} и {7} равны соответственно 0,2, 0,5, 0,3. Набор, не содержащий ни одной из этих точек, имеет нулевую вероятность.

Рисунок 5: CDF дискретного распределения вероятностей,...

Рисунок 6: ... непрерывного распределения вероятностей, ...

Рисунок 7: ... распределения, которое имеет как непрерывную, так и дискретную часть.

Дискретное распределение вероятностей — это распределение вероятностей случайной величины, которая может принимать только счетное число значений. ( почти наверняка ) это означает, что вероятность любого события $E$ может быть выражено в виде (конечной или счетно бесконечной ) суммы:

$$P(X\in E)=\sum _{\omega \in A\cap E}P(X=\omega ),$$

где $A$ представляет собой счетное множество с $P(X\in A)=1$. Таким образом, дискретные случайные величины (т.е. случайные величины, распределение вероятностей которых дискретно) — это в точности те величины, у которых есть функция массы вероятности. $p(x)=P(X=x)$. В случае, когда диапазон значений счетно бесконечен, эти значения должны снижаться до нуля достаточно быстро, чтобы сумма вероятностей составила 1. Например, если $p(n)={\tfrac {1}{2^{n}}}$ для $n=1,2,...$, сумма вероятностей будет $1/2+1/4+1/8+\dots =1$.

Хорошо известные дискретные распределения вероятностей, используемые в статистическом моделировании, включают распределение Пуассона , распределение Бернулли , биномиальное распределение , геометрическое распределение , отрицательное биномиальное распределение и категориальное распределение . Когда выборка (набор наблюдений) формируется из более крупной совокупности, точки выборки имеют дискретное эмпирическое распределение , которое предоставляет информацию о распределении совокупности. Кроме того, дискретное равномерное распределение обычно используется в компьютерных программах, которые делают случайный выбор с равной вероятностью между несколькими вариантами.

распределения

Дискретную случайную величину с действительным знаком можно эквивалентно определить как случайную величину, чья кумулятивная функция распределения увеличивается только за счет скачков , то есть ее cdf увеличивается только там, где она «перескакивает» к более высокому значению, и является постоянной в интервалах без скачков. Точки, в которых происходят скачки, и есть те значения, которые может принимать случайная величина. Таким образом, кумулятивная функция распределения имеет вид

$$F(x)=P(X\leq x)=\sum _{\omega \leq x}p(\omega ).$$

Точки, в которых происходит скачок CDF, всегда образуют счетное множество; это может быть любое счетное множество и, следовательно, оно может быть даже плотным в действительных числах.

Дирака

Дискретное распределение вероятностей часто представляется мерами Дирака , распределениями вероятностей детерминированных случайных величин . Для любого результата $\omega$, позволять $\delta _{\omega }$ быть мерой Дирака, сосредоточенной в $\omega$. Учитывая дискретное распределение вероятностей, существует счетное множество $A$ с $P(X\in A)=1$ и функция вероятностной массы $p$. Если $E$ какое-либо событие, то

$$P(X\in E)=\sum _{\omega \in A}p(\omega )\delta _{\omega }(E),$$

или короче,

$$P_{X}=\sum _{\omega \in A}p(\omega )\delta _{\omega }.$$

Аналогичным образом дискретные распределения можно представить с помощью дельта-функции Дирака как обобщенной функции плотности вероятности. $f$, где

$$f(x)=\sum _{\omega \in A}p(\omega )\delta (x-\omega ),$$

что значит

$$P(X\in E)=\int _{E}f(x)\,dx=\sum _{\omega \in A}p(\omega )\int _{E}\delta (x-\omega )=\sum _{\omega \in A\cap E}p(\omega )$$

для любого мероприятия $E.$

Представление индикаторной функции

Для дискретной случайной величины $X$, позволять $u_{0},u_{1},\dots$быть значениями, которые он может принимать с ненулевой вероятностью. Обозначим

$$\Omega _{i}=X^{-1}(u_{i})=\{\omega :X(\omega )=u_{i}\},\,i=0,1,2,\dots$$

Это непересекающиеся множества , и для таких множеств

$$P\left(\bigcup _{i}\Omega _{i}\right)=\sum _{i}P(\Omega _{i})=\sum _{i}P(X=u_{i})=1.$$

Отсюда следует, что вероятность того, что $X$ принимает любое значение, кроме $u_{0},u_{1},\dots$ равно нулю, поэтому можно написать $X$ как

$$X(\omega )=\sum _{i}u_{i}1_{\Omega _{i}}(\omega )$$

за исключением набора с нулевой вероятностью, где $1_{A}$ – индикаторная функция $A$. Это может служить альтернативным определением дискретных случайных величин.

Одноточечное распределение

Особый случай — дискретное распределение случайной величины, которая может принимать только одно фиксированное значение; другими словами, это детерминированное распределение . Формально говоря, случайная величина $X$ имеет одноточечное распределение, если имеет возможный результат $x$ такой, что $P(X{=}x)=1.$ Тогда все остальные возможные исходы имеют вероятность 0. Его кумулятивная функция распределения сразу же подскакивает от 0 до 1.

непрерывное

Основная статья: Функция плотности вероятности

Абсолютно непрерывное распределение вероятностей — это распределение вероятностей действительных чисел с бесчисленным множеством возможных значений, например целым интервалом в действительной прямой, и где вероятность любого события может быть выражена в виде интеграла. Точнее, настоящая случайная величина $X$ имеет абсолютно непрерывное распределение вероятностей, если существует функция $f:\mathbb {R} \to [0,\infty ]$ такой, что для каждого интервала $I=[a,b]\subset \mathbb {R}$ вероятность $X$ принадлежащий $I$ задается интегралом от $f$ над $I$:

$$P\left(a\leq X\leq b\right)=\int _{a}^{b}f(x)\,dx.$$

Это определение функции плотности вероятности , так что абсолютно непрерывные распределения вероятностей в точности соответствуют функции плотности вероятности. В частности, вероятность $X$ принимать какое-либо одно значение $a$ (то есть, $a\leq X\leq a$) равен нулю, поскольку интеграл с совпадающими верхним и нижним пределами всегда равен нулю. Если интервал $[a,b]$ заменяется любым измеримым множеством $A$, соответствующее равенство остается в силе:

$$P(X\in A)=\int _{A}f(x)\,dx.$$

Абсолютно непрерывная случайная величина — это случайная величина, распределение вероятностей которой абсолютно непрерывно.

Существует множество примеров абсолютно непрерывных распределений вероятностей: нормальное , равномерное , хи-квадрат и другие .

распределения

Абсолютно непрерывные распределения вероятностей, определенные выше, — это те, которые имеют абсолютно непрерывную кумулятивную функцию распределения. В этом случае кумулятивная функция распределения $F$ имеет форму

$$F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt$$

где $f$ — плотность случайной величины $X$ что касается распределения $P$.

Примечание по терминологии: абсолютно непрерывные распределения следует отличать от непрерывных распределений , которые имеют непрерывную кумулятивную функцию распределения. Каждое абсолютно непрерывное распределение является непрерывным распределением, но обратное неверно: существуют сингулярные распределения , которые не являются ни абсолютно непрерывными, ни дискретными, ни их смесью и не имеют плотности. Примером может служить распределение Кантора . Однако некоторые авторы используют термин «непрерывное распределение» для обозначения всех распределений, кумулятивная функция распределения которых абсолютно непрерывна , т.е. называют абсолютно непрерывные распределения непрерывными распределениями.

Более общее определение функций плотности и эквивалентных им абсолютно непрерывных мер см в разделе «Абсолютно непрерывная мера». .

Колмогоровское определение

Основные статьи: Вероятностное пространство и Вероятностная мера

В теоретико-мерной формализации теории вероятностей случайная величина определяется как измеримая функция. $X$ из вероятностного пространства $(\Omega ,{\mathcal {F}},\mathbb {P} )$ в измеримое пространство $({\mathcal {X}},{\mathcal {A}})$. Учитывая, что вероятности событий вида $\{\omega \in \Omega \mid X(\omega )\in A\}$ удовлетворяют аксиомам вероятности Колмогорова , распределение вероятностей $X$ это мера изображения $X_{*}\mathbb {P}$ из $X$ , который является вероятностной мерой $({\mathcal {X}},{\mathcal {A}})$ удовлетворяющий $X_{*}\mathbb {P} =\mathbb {P} X^{-1}$.

Другие виды дистрибутивов

Рисунок 8: Одно из решений уравнений Рабиновича–Фабриканта . Какова вероятность наблюдения состояния на определенном месте носителя (т. е. красном подмножестве)?

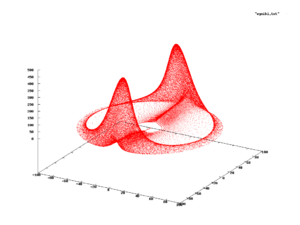
Абсолютно непрерывные и дискретные распределения с поддержкой $\mathbb {R} ^{k}$ или $\mathbb {N} ^{k}$ чрезвычайно полезны для моделирования множества явлений, поскольку большинство практических распределений поддерживаются на относительно простых подмножествах, таких как гиперкубы или шары . Однако это не всегда так, и существуют явления с опорами, которые на самом деле представляют собой сложные кривые. $\gamma :[a,b]\rightarrow \mathbb {R} ^{n}$ в некотором пространстве $\mathbb {R} ^{n}$или похожие. В этих случаях распределение вероятностей опирается на изображение такой кривой и, скорее всего, будет определено эмпирическим путем, а не поиском для него замкнутой формулы.

Один из примеров показан на рисунке справа, где показана эволюция системы дифференциальных уравнений (широко известных как уравнения Рабиновича – Фабриканта ), которые можно использовать для моделирования поведения ленгмюровских волн в плазме . Когда это явление изучается, наблюдаемые состояния из подмножества обозначены красным. Таким образом, можно было бы спросить, какова вероятность наблюдения состояния в определенной позиции красного подмножества; если такая вероятность существует, она называется вероятностной мерой системы.

Такая сложная поддержка довольно часто встречается в динамических системах . Установить, что система имеет вероятностную меру, непросто, и основная проблема заключается в следующем. Позволять $t_{1}\ll t_{2}\ll t_{3}$ быть мгновениями во времени и $O$подмножество поддержки; если для системы существует вероятностная мера, можно было бы ожидать, что частота наблюдения состояний внутри множества $O$ будет равен интервалу $[t_{1},t_{2}]$ и $[t_{2},t_{3}]$, чего может не случиться; например, он может колебаться подобно синусу, $\sin(t)$, предел которого, когда $t\rightarrow \infty$не сходится. Формально мера существует только в том случае, если предел относительной частоты сходится при наблюдении системы в бесконечное будущее. Разделом динамических систем, изучающим существование вероятностной меры, является эргодическая теория .

Обратите внимание, что даже в этих случаях распределение вероятностей, если оно существует, все равно можно было бы назвать «абсолютно непрерывным» или «дискретным» в зависимости от того, является ли носитель несчетным или счетным соответственно.

Генерация случайных чисел

Основная статья: Выборка псевдослучайных чисел

Большинство алгоритмов основаны на генераторе псевдослучайных чисел , который выдаёт числа. $X$равномерно распределенные в полуинтервале [0, 1) . Эти случайные переменные $X$затем преобразуются с помощью некоторого алгоритма для создания новой случайной величины, имеющей требуемое распределение вероятностей. С помощью этого источника однородной псевдослучайности можно генерировать реализации любой случайной величины.

Например, предположим $U$ имеет равномерное распределение между 0 и 1. Чтобы построить случайную переменную Бернулли для некоторого $0<p<1$, мы определяем

$$X={\begin{cases}1,&{\text{if }}U<p\\0,&{\text{if }}U\geq p\end{cases}}$$

так что

$$\Pr(X=1)=\Pr(U<p)=p,\quad \Pr(X=0)=\Pr(U\geq p)=1-p.$$

Эта случайная величина X имеет распределение Бернулли с параметром $p$. Это преобразование дискретной случайной величины.

Для функции распределения $F$ из абсолютно непрерывной случайной величины необходимо построить абсолютно непрерывную случайную величину. $F^{\mathit {inv}}$, обратная функция $F$, относится к единой переменной $U$:

$${U\leq F(x)}={F^{\mathit {inv}}(U)\leq x}.$$

Например, предположим, что случайная величина имеет экспоненциальное распределение. $F(x)=1-e^{-\lambda x}$ должен быть построен.

$${\begin{aligned}F(x)=u&\Leftrightarrow 1-e^{-\lambda x}=u\\[2pt]&\Leftrightarrow e^{-\lambda x}=1-u\\[2pt]&\Leftrightarrow -\lambda x=\ln(1-u)\\[2pt]&\Leftrightarrow x={\frac {-1}{\lambda }}\ln(1-u)\end{aligned}}$$

так $F^{\mathit {inv}}(u)={\frac {-1}{\lambda }}\ln(1-u)$ и если $U$ имеет $U(0,1)$ распределение, то случайная величина $X$ определяется $X=F^{\mathit {inv}}(U)={\frac {-1}{\lambda }}\ln(1-U)$. Это имеет экспоненциальное распределение $\lambda$.

Частой проблемой при статистическом моделировании ( метод Монте-Карло ) является генерация псевдослучайных чисел , которые распределяются заданным образом.

распределения вероятностей и

Более полный список см. в разделе Список распределений вероятностей .

Концепция распределения вероятностей и описываемых ими случайных величин лежит в основе математической дисциплины теории вероятностей и статистики. Существует разброс или изменчивость практически любой величины, которую можно измерить в популяции (например, рост людей, долговечность металла, рост продаж, транспортный поток и т. д.); почти все измерения производятся с некоторой основной погрешностью; В физике многие процессы описываются вероятностно, от кинетических свойств газов до квантовомеханического описания элементарных частиц . По этим и многим другим причинам простые числа часто недостаточны для описания величины, в то время как распределения вероятностей часто более подходят.

Ниже приводится список некоторых наиболее распространенных распределений вероятностей, сгруппированных по типу процесса, к которому они относятся. Более полный список см. в списке вероятностных распределений , которые группируются по характеру рассматриваемого результата (дискретные, абсолютно непрерывные, многомерные и т. д.).

Все приведенные ниже одномерные распределения имеют один пик; то есть предполагается, что значения группируются вокруг одной точки. На практике фактически наблюдаемые величины могут группироваться вокруг нескольких значений. Такие количества можно смоделировать с помощью распределения смеси .

Линейный рост (например, ошибки, смещения)

• Нормальное распределение (распределение Гаусса) для одной такой величины; наиболее часто используемое абсолютно непрерывное распределение

Экспоненциальный рост (например, цен, доходов, населения)

• Логарифмически нормальное распределение для одной такой величины, журнал которой нормально распределен .
• Распределение Парето для одной такой величины, журнал которой распределен экспоненциально ; прототипическое степенное распределение

Равномерно распределенные количества

• Дискретное равномерное распределение для конечного набора значений (например, результат игры в кости)
• Непрерывное равномерное распределение для абсолютно непрерывно распределенных значений

заданной вероятностью

• Основные дистрибутивы:
  • Распределение Бернулли для результатов одного испытания Бернулли (например, успех/неудача, да/нет)
  • Биномиальное распределение количества «положительных событий» (например, успехов, голосов «да» и т. д.) при фиксированном общем количестве независимых событий.
  • Отрицательное биномиальное распределение для наблюдений биномиального типа, но где интересующей величиной является количество неудач до того, как произойдет заданное количество успехов.
  • Геометрическое распределение для наблюдений биномиального типа, но где интересующей величиной является количество неудач до первого успеха; частный случай отрицательного биномиального распределения
• Относится к схемам выборки для конечной совокупности:
  • Гипергеометрическое распределение количества «положительных вхождений» (например, успехов, голосов «да» и т. д.) при фиксированном общем количестве вхождений с использованием выборки без замены.
  • Бета-биномиальное распределение для количества «положительных вхождений» (например, успехов, голосов «да» и т. д.) при фиксированном общем количестве вхождений, выборка с использованием модели урны Пойа (в некотором смысле «противоположность» выборке без замены )

(события с K возможными

• Категориальное распределение для одного категориального результата (например, да/нет/может быть в опросе); обобщение распределения Бернулли
• Полиномиальное распределение для количества каждого типа категориального результата при фиксированном общем количестве результатов; обобщение биномиального распределения
• Многомерное гипергеометрическое распределение , аналогичное полиномиальному распределению , но с использованием выборки без замены ; обобщение гипергеометрического распределения

происходящие независимо с заданной скоростью

• Распределение Пуассона для количества появлений события типа Пуассона за заданный период времени.
• Экспоненциальное распределение за время до наступления следующего события типа Пуассона.
• Распределение гамма-излучения за время до возникновения следующих k событий пуассоновского типа.

Абсолютные значения векторов с

• Распределение Рэлея для распределения векторных величин с гауссово распределенными ортогональными компонентами. Распределения Рэлея обнаруживаются в радиочастотных сигналах с гауссовыми действительными и мнимыми компонентами.
• Распределение Райса — обобщение распределений Рэлея для случаев, когда имеется стационарная составляющая фонового сигнала. Обнаруживается в затухании радиосигналов по Райсу из-за многолучевого распространения и в МР-изображениях с шумовым искажением ненулевых сигналов ЯМР.

суммой

• Распределение хи-квадрат — распределение суммы квадратов стандартных нормальных переменных; полезно, например, для вывода относительно выборочной дисперсии нормально распределенных выборок (см. тест хи-квадрат )
• Распределение Стьюдента , распределение отношения стандартной нормальной переменной и квадратного корня из масштабированной переменной хи-квадрат ; полезен для вывода о среднем значении нормально распределенных выборок с неизвестной дисперсией (см. t-критерий Стьюдента )
• F-распределение , распределение отношения двух масштабированных хи-квадрат переменных ; полезно, например, для выводов, которые включают сравнение дисперсий или R-квадрат (квадрат коэффициента корреляции )

сопряженные априорные распределения в

Основная статья: Сопряженный априор

• Бета-распределение для одной вероятности (действительное число от 0 до 1); сопряжено с распределением Бернулли и биномиальным распределением
• Гамма-распределение для неотрицательного параметра масштабирования; сопряжен с параметром скорости распределения Пуассона или экспоненциального распределения , точностью (обратной дисперсией ) нормального распределения и т. д.
• Распределение Дирихле для вектора вероятностей, сумма которых должна быть равна 1; сопряжено с категориальным распределением и полиномиальным распределением ; обобщение бета-распределения
• Распределение Уишарта для симметричной неотрицательно определенной матрицы; сопряжено с обратной ковариационной матрицей многомерного нормального распределения ; обобщение гамма-распределения

вероятностных

• Модели кэш-языка и другие статистические модели языка , используемые при обработке естественного языка для назначения вероятностей появления определенных слов и последовательностей слов, делают это посредством вероятностных распределений.
• В квантовой механике плотность вероятности обнаружения частицы в данной точке пропорциональна квадрату величины волновой функции частицы в этой точке (см. правило Борна ). Следовательно, функция распределения вероятностей положения частицы описывается выражением ${\textstyle P_{a\leq x\leq b}(t)=\int _{a}^{b}dx\,|\Psi (x,t)|^{2}}$, вероятность того, что положение частицы x будет находиться в интервале a ≤ x ≤ b в первом измерении, и аналогичный тройной интеграл в третьем измерении. Это ключевой принцип квантовой механики.
• Вероятностный поток нагрузки при исследовании потока мощности объясняет неопределенности входных переменных как распределение вероятностей и обеспечивает расчет потока мощности также с точки зрения распределения вероятностей.
• Прогнозирование возникновения природных явлений на основе предыдущих распределений частот , таких как тропические циклоны , град, время между событиями и т. д.

Установка

Этот раздел представляет собой отрывок из описания распределения вероятностей . [ редактировать ]

Подбор распределения вероятностей или просто подбор распределения — это подбор распределения вероятностей к ряду данных, касающихся повторных измерений переменного явления. Целью подбора распределения является частоты возникновения предсказание вероятности величины или явления в определенном интервале.

Существует множество распределений вероятностей (см. список распределений вероятностей ), из которых некоторые можно более точно подогнать к наблюдаемой частоте данных, чем другие, в зависимости от характеристик явления и распределения. Предполагается, что распределение, дающее точное соответствие, приведет к хорошим прогнозам.

Поэтому при подборе распределения необходимо выбрать распределение, которое хорошо соответствует данным.

См. также

• Условное распределение вероятностей
• Эмпирическое распределение вероятностей
• Гистограмма
• Совместное распределение вероятностей
• Вероятностная мера
• Распределение квазивероятностей
• Приложение интеграла Римана–Стилтьеса к теории вероятностей

Списки

• Список вероятностных распределений
• Список статистических тем

Ссылки

Источники

• ден Деккер, AJ; Сийберс, Дж. (2014). «Распределение данных на магнитно-резонансных изображениях: обзор». Физика Медика . 30 (7): 725–741. дои : 10.1016/j.ejmp.2014.05.002 . ПМИД   25059432 .
• Вапник, Владимир Наумович (1998). Статистическая теория обучения . Джон Уайли и сыновья.

Внешние ссылки

• «Распределение вероятностей» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Полевое руководство по непрерывным распределениям вероятностей , Гэвин Э. Крукс.
• Различение вероятностной меры, функции и распределения