Гомоскедастичность и гетероскедастичность

График со случайными данными, показывающий гомоскедастичность: при каждом значении x значение y точек имеет примерно одинаковую дисперсию .

График со случайными данными, показывающий гетероскедастичность: дисперсия значений y точек увеличивается с увеличением значений x .

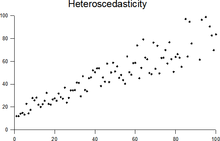
В статистике последовательность , является случайных величин гомоскедастической ( / ˌ h oʊ m oʊ s k ə ˈ d æ s t ɪ k / ) если все ее случайные величины имеют одинаковую конечную дисперсию ; это также известно как однородность дисперсии . Дополнительное понятие называется гетероскедастичностью , также известной как гетерогенность дисперсии . варианты написания homos k edasticity и гетероs k edasticity Также часто используются . Скедастичность происходит от древнегреческого слова skedánnymi, что означает «рассеивать». Предположение, что переменная гомоскедастична, тогда как на самом деле она гетероскедастична ( / ˌ h ɛ t ər oʊ s k ə ˈ d æ s t ɪ k / ) приводит к несмещенным, но неэффективным точечным оценкам и к смещенным оценкам стандартных ошибок , и может привести к переоценка степени соответствия , измеряемой коэффициентом Пирсона .

Существование гетероскедастичности является серьезной проблемой в регрессионном анализе и дисперсионном анализе , поскольку оно делает недействительными статистические тесты значимости , которые предполагают, что все ошибки моделирования имеют одинаковую дисперсию. Хотя обычная оценка методом наименьших квадратов по-прежнему несмещена при наличии гетероскедастичности, она неэффективна, а выводы, основанные на предположении о гомоскедастичности, вводят в заблуждение. В этом случае метод обобщенных наименьших квадратов (GLS). в прошлом часто использовался В настоящее время стандартной практикой в ​​​​эконометрике является включение стандартных ошибок, согласованных с гетероскедастичностью , вместо использования GLS, поскольку GLS может демонстрировать сильную погрешность в небольших выборках, если фактическая скедастическая функция неизвестна.

Поскольку гетероскедастичность касается ожиданий второго момента ошибки, ее наличие называется некорректной спецификацией второго порядка.

Эконометрист при наличии гетероскедастичности, которые привели к Роберт Энгл был удостоен Нобелевской премии по экономике 2003 года за исследования регрессионного анализа формулировке метода моделирования авторегрессионной условной гетероскедастичности (ARCH).

Определение

Рассмотрим линейной регрессии уравнение $y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,$ где зависимая случайная величина $y_{i}$ равна детерминированной переменной $x_{i}$ коэффициент умножения $\beta _{i}$ плюс случайный член возмущения $\varepsilon _{i}$ это означает ноль. Возмущения гомоскедастичны, если дисперсия $\varepsilon _{i}$ является константой $\sigma ^{2}$; в противном случае они гетероскедастичны. В частности, возмущения гетероскедастичны, если дисперсия $\varepsilon _{i}$ зависит от $i$ или от стоимости $x_{i}$. Один из способов, которым они могут быть гетероскедастическими, заключается в том, что $\sigma _{i}^{2}=x_{i}\sigma ^{2}$ (пример скедастической функции ), поэтому дисперсия пропорциональна значению $x$.

В более общем смысле, если дисперсионно-ковариационная матрица возмущения $\varepsilon _{i}$ через $i$ имеет непостоянную диагональ, возмущение гетероскедастическое. Приведенные ниже матрицы представляют собой ковариации, когда во времени имеется всего три наблюдения. Возмущение в матрице A гомоскедастично; это простой случай, когда OLS является лучшим линейным несмещенным оценщиком. Возмущения в матрицах B и C являются гетероскедастическими. В матрице B дисперсия меняется во времени и постоянно увеличивается во времени; в матрице C дисперсия зависит от значения $x$. Нарушение в матрице D является гомоскедастическим, поскольку диагональные дисперсии постоянны, даже несмотря на то, что недиагональные ковариации отличны от нуля, а обычный метод наименьших квадратов неэффективен по другой причине: серийная корреляция.

${\begin{aligned}A&=\sigma ^{2}{\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}}&B&=\sigma ^{2}{\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\\\end{bmatrix}}&C&=\sigma ^{2}{\begin{bmatrix}x_{1}&0&0\\0&x_{2}&0\\0&0&x_{3}\\\end{bmatrix}}&D&=\sigma ^{2}{\begin{bmatrix}1&\rho &\rho ^{2}\\\rho &1&\rho \\\rho ^{2}&\rho &1\\\end{bmatrix}}\end{aligned}}$

Примеры

Гетероскедастичность часто возникает, когда существует большая разница в размерах наблюдений.

Классическим примером гетероскедастичности является соотношение доходов и расходов на питание. Богатый человек может иногда есть недорогую еду, а иногда и дорогую. Бедный человек почти всегда будет есть недорогую еду. Таким образом, люди с более высокими доходами демонстрируют большую вариативность расходов на питание.

При запуске ракеты наблюдатель измеряет расстояние, пройденное ракетой, один раз в секунду. В первые пару секунд измерения могут быть точными до ближайшего сантиметра. Через пять минут точность измерений может быть хорошей только до 100 м из-за увеличения расстояния, атмосферных искажений и множества других факторов. Таким образом, измерения расстояний могут проявлять гетероскедастичность.

Последствия

Одним из предположений классической модели линейной регрессии является отсутствие гетероскедастичности. Нарушение этого предположения означает, что теорема Гаусса-Маркова неприменима, а это означает, что оценщики OLS не являются лучшими линейными несмещенными оценщиками (СИНИЙ) , а их дисперсия не является самой низкой среди всех других несмещенных оценщиков.Гетероскедастичность не приводит к смещению оценок обычных коэффициентов наименьших квадратов, хотя она может привести к смещению обычных оценок дисперсии (и, следовательно, стандартных ошибок) коэффициентов по методу наименьших квадратов, возможно, выше или ниже истинной дисперсии генеральной совокупности. Таким образом, регрессионный анализ с использованием гетероскедастических данных по-прежнему обеспечит несмещенную оценку связи между переменной-предиктором и результатом, но стандартные ошибки и, следовательно, выводы, полученные в результате анализа данных, являются подозрительными. Смещенные стандартные ошибки приводят к смещенным выводам, поэтому результаты проверки гипотез могут быть неверными. Например, если МНК выполняется на гетероскедастическом наборе данных, что дает смещенную оценку стандартной ошибки, исследователь может не отклонить нулевую гипотезу при данном уровень значимости , когда эта нулевая гипотеза фактически не характерна для реальной популяции (совершая ошибку II рода ).

При определенных предположениях оценка OLS имеет нормальное асимптотическое распределение , если она правильно нормализована и центрирована (даже если данные не получены из нормального распределения ). Этот результат используется для обоснования использования нормального распределения или распределения хи-квадрат (в зависимости от того, как статистика теста рассчитывается ) при проведении проверки гипотезы . Это справедливо даже в условиях гетероскедастичности. Точнее, оценка OLS при наличии гетероскедастичности является асимптотически нормальной, если она правильно нормирована и центрирована, с дисперсионно-ковариационной матрицей , которая отличается от случая гомоскедастичности. В 1980 году Уайт предложил непротиворечивую оценку дисперсионно-ковариационной матрицы асимптотического распределения оценки OLS. Это подтверждает использование проверки гипотез с использованием оценок OLS и оценки дисперсии-ковариации Уайта в условиях гетероскедастичности.

Гетероскедастичность также является важной практической проблемой, возникающей в задачах ANOVA . все F-тест еще можно использовать в некоторых обстоятельствах.

Однако было сказано, что студентам, изучающим эконометрику, не следует слишком остро реагировать на гетероскедастичность. Один автор написал: «Неравную дисперсию ошибок стоит исправлять только тогда, когда проблема серьезна». Кроме того, еще одно предостережение заключалось в следующем: «Гетероскедастичность никогда не была причиной отказа от хорошей в других отношениях модели». С появлением стандартных ошибок, совместимых с гетероскедастичностью, позволяющих делать выводы без указания условного второго момента ошибки, проверка условной гомоскедастичности не так важна, как в прошлом.

Однако для любой нелинейной модели (например, моделей Logit и Probit ) гетероскедастичность имеет более серьезные последствия: оценки максимального правдоподобия (MLE) параметров обычно будут смещенными, а также противоречивыми (если функция правдоподобия не будет изменена на правильно учесть точную форму гетероскедастичности или распределение является членом линейного экспоненциального семейства и правильно задана условная функция ожидания). Тем не менее, в контексте моделей бинарного выбора ( Logit или Probit ) гетероскедастичность приведет только к положительному эффекту масштабирования на асимптотическом среднем неправильно заданном MLE (т. е. модели, которая игнорирует гетероскедастичность). В результате прогнозы, основанные на неверно указанном MLE, останутся верными. Кроме того, неправильно заданные MLE Probit и Logit будут асимптотически нормально распределены, что позволяет выполнять обычные тесты значимости (с соответствующей дисперсионно-ковариационной матрицей). Однако, что касается проверки общей гипотезы, как отметил Грин , «простое вычисление устойчивой ковариационной матрицы для несовместимой в других отношениях оценки не дает ее оправдания. Следовательно, ценность устойчивой ковариационной матрицы в этой ситуации неясна».

Исправление

Существует несколько распространенных поправок на гетероскедастичность. Они есть:

• Стабилизирующее преобразование данных, например, логарифмизированных данных. Нелогарифмированные ряды, растущие экспоненциально, часто имеют увеличивающуюся изменчивость по мере увеличения ряда с течением времени. Однако изменчивость в процентном выражении может быть довольно стабильной.
• Используйте другую спецификацию модели (другие переменные X или, возможно, нелинейные преобразования переменных X ).
• Примените метод взвешенной оценки наименьших квадратов , в котором OLS применяется к преобразованным или взвешенным значениям X и Y . Веса варьируются в зависимости от наблюдений, обычно в зависимости от изменения дисперсии ошибок. В одном варианте веса напрямую связаны с величиной зависимой переменной, и это соответствует процентной регрессии по методу наименьших квадратов.
• Стандартные ошибки, согласованные с гетероскедастичностью (HCSE), хотя и являются предвзятыми, улучшают оценки OLS. HCSE — это последовательная оценка стандартных ошибок в регрессионных моделях с гетероскедастичностью. Этот метод корректирует гетероскедастичность без изменения значений коэффициентов. Этот метод может превосходить обычный МНК, поскольку, если присутствует гетероскедастичность, он ее корректирует, однако, если данные гомоскедастичны, стандартные ошибки эквивалентны обычным стандартным ошибкам, оцениваемым с помощью МНК. Несколько модификаций метода Уайта вычисления стандартных ошибок, совместимых с гетероскедастичностью, были предложены в качестве поправок с превосходными свойствами конечной выборки.
• Дикая загрузка может использоваться в качестве метода повторной выборки , который учитывает различия в условной дисперсии термина ошибки. Альтернативой является повторная выборка наблюдений вместо ошибок. Обратите внимание, что ошибки повторной выборки без учета связанных значений наблюдения приводят к гомоскедастичности и, таким образом, приводят к неверным выводам.
• Используйте MINQUE или даже обычные оценщики. ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ (для $i=1,2,...,k$ независимые образцы с $j=1,2,...,n_{i}$ наблюдений каждое), потери эффективности которых не существенны при большом числе наблюдений на выборку ( $n_{i}>5$), особенно для небольшого количества независимых выборок.

Тестирование

Абсолютное значение остатков для смоделированных гетероскедастических данных первого порядка

Остатки можно проверить на гомоскедастичность с помощью теста Бреуша-Пэгана . который выполняет вспомогательную регрессию квадратов остатков по независимым переменным. Из этой вспомогательной регрессии сохраняется объясненная сумма квадратов, деленная на два, а затем становится тестовой статистикой для распределения хи-квадрат со степенями свободы, равными числу независимых переменных. Нулевой гипотезой этого теста хи-квадрат является гомоскедастичность, а альтернативная гипотеза будет указывать на гетероскедастичность. Поскольку критерий Бреуша-Пэгана чувствителен к отклонениям от нормальности или небольшому размеру выборки, вместо него обычно используется тест Кенкера-Бассетта или «обобщенный критерий Бреуша-Пэгана». Из вспомогательной регрессии оно сохраняет значение R-квадрата, которое затем умножается на размер выборки, а затем становится тестовой статистикой для распределения хи-квадрат (и использует те же степени свободы). Хотя это не является необходимым для теста Кенкера-Бассетта, тест Бреуша-Пэгана требует, чтобы квадраты остатков также были разделены на остаточную сумму квадратов, разделенную на размер выборки. Проверка групповой гетероскедастичности может быть выполнена с помощью теста Гольдфельда-Квандта .

Из-за стандартного использования стандартных ошибок, согласованных с гетероскедастичностью , и проблемы предварительного тестирования специалисты по эконометрике в настоящее время редко используют тесты на условную гетероскедастичность.

Список тестов

Хотя тесты на гетероскедастичность между группами формально можно рассматривать как частный случай тестирования в рамках регрессионных моделей, некоторые тесты имеют структуры, специфичные для этого случая.

Тесты в регрессии

• Тест Гольдфельда – Квандта
• Парковый тест
• тест Глейзера
• Тест Харрисона-Маккейба
• Тест Бреуша – Пэгана
• Белый тест
• Тест Кука – Вейсберга

Тесты для сгруппированных данных

• F-критерий равенства дисперсий
• C-тест Кокрена
• тест Хартли
• тест Бартлетта
• тест Левена
• Тест Брауна-Форсайта

Обобщения

распределения

Два или более нормальных распределения , $N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),$ оба гомоскедастичны и не имеют серийной корреляции, если они имеют одни и те же диагонали в своей ковариационной матрице, $\Sigma _{1}{ii}=\Sigma _{2}{jj},\ \forall i=j.$ и их недиагональные элементы равны нулю. Гомоскедастические распределения особенно полезны для построения алгоритмов статистического распознавания образов и машинного обучения . Одним из популярных примеров алгоритма, предполагающего гомоскедастичность, является линейный дискриминантный анализ Фишера .Понятие гомоскедастичности можно применить к распределениям по сферам.

Многомерные данные

Изучение домашней скедастичности и гетероскедастичности было обобщено на многомерный случай, который касается ковариаций векторных наблюдений вместо дисперсии скалярных наблюдений. Один из вариантов этого заключается в использовании ковариационных матриц в качестве многомерной меры дисперсии. Некоторые авторы рассматривали тесты в этом контексте как для ситуаций регрессии, так и для ситуаций с сгруппированными данными. Тест Бартлетта на гетероскедастичность между сгруппированными данными, чаще всего используемый в одномерном случае, также был расширен для многомерного случая, но приемлемое решение существует только для двух групп. Аппроксимации существуют для более чем двух групп, и обе они называются М-тестом Бокса .

См. также

• Неоднородность
• Сферическая ошибка
• Стандартные ошибки, согласованные с гетероскедастичностью

Дальнейшее чтение

Большинство учебников по статистике будут включать по крайней мере некоторый материал по гомоскедастичности и гетероскедастичности. Некоторые примеры:

• Астериу, Димитрос; Холл, Стивен Г. (2011). Прикладная эконометрика (второе изд.). Пэлгрейв Макмиллан. стр. 109–147. ISBN  978-0-230-27182-1 .
• Дэвидсон, Рассел; Маккиннон, Джеймс Г. (1993). Оценка и вывод в эконометрике . Нью-Йорк: Издательство Оксфордского университета. стр. 547–582. ISBN  978-0-19-506011-9 .
• Догерти, Кристофер (2011). Введение в эконометрику . Нью-Йорк: Издательство Оксфордского университета. стр. 280–299. ISBN  978-0-19-956708-9 .
• Гуджарати, Дамодар Н .; Портер, Дон К. (2009). Основная эконометрика (Пятое изд.). Нью-Йорк: МакГроу-Хилл Ирвин. стр. 365–411. ISBN  978-0-07-337577-9 .
• Кмента, Ян (1986). Элементы эконометрики (второе изд.). Нью-Йорк: Макмиллан. стр. 269–298 . ISBN  978-0-02-365070-3 .
• Маддала, GS ; Лахири, Каджал (2009). Введение в эконометрику (Четвертое изд.). Нью-Йорк: Уайли. стр. 211–238. ISBN  978-0-470-01512-4 .

Внешние ссылки

• по эконометрике (тема: гетероскедастичность) на YouTube Лекция Марка Тома