Изотоническая регрессия

Пример изотонической регрессии (сплошная красная линия) по сравнению с линейной регрессией на тех же данных, оба подходят для минимизации среднеквадратической ошибки . Свойство изотонической регрессии в свободной форме означает, что линия может быть круче там, где данные круче; ограничение изотоничности означает, что линия не уменьшается.

В статистике и анализе численном изотоническая регрессия или монотонная регрессия — это метод подгонки линии произвольной формы к последовательности наблюдений так, чтобы подобранная линия не убывала (или не возрастала) повсюду и лежала как можно ближе к наблюдениям. насколько это возможно.

Приложения

Изотоническая регрессия имеет применение в статистических выводах . Например, его можно использовать для подгонки изотонической кривой к средним значениям некоторого набора экспериментальных результатов, когда ожидается увеличение этих средних в соответствии с некоторым конкретным порядком. Преимущество изотонической регрессии заключается в том, что она не ограничена какой-либо функциональной формой, такой как линейность, налагаемая линейной регрессией , пока функция монотонно возрастает.

Другое применение — неметрическое многомерное масштабирование . низкоразмерное вложение где ищется для точек данных, чтобы порядок расстояний между точками во вложении соответствовал порядку несходства между точками. Изотоническая регрессия используется итеративно для подбора идеальных расстояний и сохранения порядка относительного несходства.

Изотоническая регрессия также используется в вероятностной классификации для калибровки прогнозируемых вероятностей моделей машинного обучения с учителем .

Изотоническая регрессия для просто упорядоченного случая с одномерной $x,y$ был применен для оценки непрерывной зависимости «доза-реакция» в таких областях, как анестезиология и токсикология. Строго говоря, изотоническая регрессия дает только точечные оценки при наблюдаемых значениях $x.$ Оценка полной кривой «доза-реакция» без каких-либо дополнительных предположений обычно выполняется посредством линейной интерполяции между точечными оценками.

разработано программное обеспечение для расчета изотонной (монотонной) регрессии Для R . Стата и Питон .

Постановка задачи и алгоритмы

Позволять $(x_{1},y_{1}),\ldots ,(x_{n},y_{n})$ быть заданным набором наблюдений, где $y_{i}\in \mathbb {R}$ и $x_{i}$ попадают в некоторое частично упорядоченное множество . Для общности каждое наблюдение $(x_{i},y_{i})$ может быть присвоен вес $w_{i}\geq 0$, хотя обычно $w_{i}=1$ для всех $i$.

Изотоническая регрессия ищет взвешенную методом наименьших квадратов. аппроксимацию ${\hat {y}}_{i}\approx y_{i}$ для всех $i$, при условии, что ${\hat {y}}_{i}\leq {\hat {y}}_{j}$ в любое время $x_{i}\leq x_{j}$. Это дает следующую квадратичную программу (QP) в переменных ${\hat {y}}_{1},\ldots ,{\hat {y}}_{n}$:

$\min \sum _{i=1}^{n}w_{i}({\hat {y}}_{i}-y_{i})^{2}$ при условии ${\hat {y}}_{i}\leq {\hat {y}}_{j}{\text{ for all }}(i,j)\in E$

где $E=\{(i,j):x_{i}\leq x_{j}\}$ определяет частичный порядок наблюдаемых входных данных $x_{i}$ (и может рассматриваться как множество ребер некоторого ориентированного ациклического графа (dag) с вершинами $1,2,\ldots n$). Проблемы этой формы могут быть решены с помощью общих методов квадратичного программирования.

В обычной обстановке, когда $x_{i}$ значения попадают в полностью упорядоченный набор, такой как $\mathbb {R}$, мы можем предположить, что WLOG , что наблюдения были отсортированы так, что $x_{1}\leq x_{2}\leq \cdots \leq x_{n}$, и возьми $E=\{(i,i+1):1\leq i<n\}$. В этом случае простым итерационным алгоритмом решения квадратичной программы является алгоритм соседнего пула нарушителей . И наоборот, Бест и Чакраварти. изучил проблему как проблему идентификации активного множества и предложил простой алгоритм. Эти два алгоритма можно рассматривать как двойственные друг другу, и оба имеют вычислительную сложность $O(n)$ на уже отсортированных данных.

Чтобы выполнить задачу изотонической регрессии, мы можем выбрать любую неубывающую функцию. $f(x)$ такой, что $f(x_{i})={\hat {y}}_{i}$ для всех я. Любая такая функция, очевидно, решает

$\min _{f}\sum _{i=1}^{n}w_{i}(f(x_{i})-y_{i})^{2}$ при условии $f$ будучи неубывающим

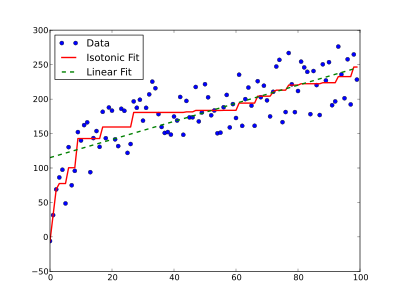
и может быть использован для прогнозирования $y$ значения для новых значений $x$. Обычный выбор, когда $x_{i}\in \mathbb {R}$ было бы линейно интерполировать между точками $(x_{i},{\hat {y}}_{i})$, как показано на рисунке, что дает непрерывную кусочно-линейную функцию:

$f(x)={\begin{cases}{\hat {y}}_{1}&{\text{if }}x\leq x_{1}\\{\hat {y}}_{i}+{\frac {x-x_{i}}{x_{i+1}-x_{i}}}({\hat {y}}_{i+1}-{\hat {y}}_{i})&{\text{if }}x_{i}\leq x\leq x_{i+1}\\{\hat {y}}_{n}&{\text{if }}x\geq x_{n}\end{cases}}$

Центрированная

Как показывает первый рисунок статьи, при наличии нарушений монотонности результирующая интерполированная кривая будет иметь пологие (постоянные) интервалы. В приложениях дозозависимого реагирования обычно известно, что $f(x)$ не только монотонно, но и гладко . Плоские интервалы несовместимы с $f(x)$принимает предполагаемую форму и может оказаться предвзятым. Простое усовершенствование для таких приложений, названное центрированной изотонической регрессией (CIR), было разработано Ороном и Флурнуа и показало, что оно существенно уменьшает ошибку оценки как для приложений, связанных с ответом на дозу, так и для приложений по определению дозы. И CIR, и стандартная изотоническая регрессия для одномерного, просто упорядоченного случая реализованы в пакете R «cir». Этот пакет также предоставляет аналитические оценки доверительного интервала.

Дальнейшее чтение

• Робертсон, Т.; Райт, FT; Дикстра, Р.Л. (1988). Заказать ограниченный статистический вывод . Нью-Йорк: Уайли. ISBN  978-0-471-91787-8 .
• Барлоу, RE; Варфоломей, диджей; Бремнер, Дж. М.; Бранк, HD (1972). Статистический вывод при ограничениях порядка; теория и применение изотонической регрессии . Нью-Йорк: Уайли. ISBN  978-0-471-04970-8 .
• Шайвли Т.С., Сагер Т.В., Уокер С.Г. (2009). «Байесовский подход к оценке непараметрической монотонной функции». Журнал Королевского статистического общества, серия B. 71 (1): 159–175. CiteSeerX   10.1.1.338.3846 . дои : 10.1111/j.1467-9868.2008.00677.x . S2CID   119761196 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Ву, ВБ ; Вудруф, М .; Ментц, Г. (2001). «Изотоническая регрессия: еще один взгляд на проблему точек перехода». Биометрика . 88 (3): 793–804. дои : 10.1093/biomet/88.3.793 .