Ковариационный анализ
Ковариационный анализ ( ANCOVA ) — это общая линейная модель , сочетающая в себе ANOVA и регрессию . ли средние значения зависимой переменной ANCOVA оценивает , равны (DV) на всех уровнях одной или нескольких категориальных независимых переменных (IV) и одной или нескольких непрерывных переменных. Например, категориальная переменная(и) может описывать лечение, а непрерывная(ые) переменная(и) может быть ковариатами или переменными, вызывающими неудобство; или наоборот. Математически ANCOVA разлагает дисперсию DV на дисперсию, объясняемую CV(s), дисперсию, объясняемую категориальным IV, и остаточную дисперсию. Интуитивно, ANCOVA можно рассматривать как «корректировку» DV с помощью групповых средств CV(ов). [1]
Модель ANCOVA предполагает линейную зависимость между ответом (DV) и ковариатой (CV):
В этом уравнении ДВ, – j-е наблюдение в i-й категориальной группе; резюме, — это j -е наблюдение ковариаты в i -й группе. Переменные в модели, полученные на основе наблюдаемых данных: (большое среднее) и (глобальное среднее значение ковариаты ). Переменные, которые необходимо подогнать: (эффект i -го уровня категориальной IV), (наклон линии) и (ассоциированный член ненаблюдаемой ошибки для j -го наблюдения в i -й группе).
Согласно этой спецификации, сумма эффектов категориальной обработки равна нулю. Также предполагается, что стандартные предположения модели линейной регрессии выполняются, как описано ниже. [2]
Использует [ править ]
Увеличить мощность [ править ]
ANCOVA можно использовать для увеличения статистической мощности (вероятности обнаружения значительной разницы ошибок внутри группы между группами, если таковая существует) за счет уменьшения дисперсии . [3] Чтобы понять это, необходимо понять тест, используемый для оценки различий между группами, F-тест . - критерий F рассчитывается путем деления объясненной дисперсии между группами (например, различий в выздоровлении) на необъяснимую дисперсию внутри групп. Таким образом,
Если это значение превышает критическое значение, мы приходим к выводу, что существует значительная разница между группами. Необъяснимая дисперсия включает в себя ошибки дисперсии (например, индивидуальные различия), а также влияние других факторов. Поэтому влияние CV сгруппировано в знаменателе. Когда мы контролируем влияние CV на DV, мы удаляем его из знаменателя, увеличивая F , тем самым увеличивая нашу способность обнаружить значительный эффект, если он вообще существует.

Корректировка ранее существовавших различий [ править ]
Другое использование ANCOVA — корректировка ранее существовавших различий в неэквивалентных (неповрежденных) группах. Это спорное заявление направлено на исправление первоначальных групповых различий (до группового распределения), которые существуют при ДВ между несколькими интактными группами. В этой ситуации участников невозможно уравнять путем случайного распределения, поэтому резюме используются для корректировки баллов и придания участникам большего сходства, чем без резюме. Однако даже при использовании ковариат не существует статистических методов, которые могли бы уравнять неравные группы. Более того, CV может быть настолько тесно связан с категориальным IV, что удаление отклонения DV, связанного с CV, устранит значительную дисперсию DV, делая результаты бессмысленными. [4]
Предположения [ править ]
Существует несколько ключевых предположений, которые лежат в основе использования ANCOVA и влияют на интерпретацию результатов. [2] Стандартные предположения линейной регрессии верны; далее мы предполагаем, что наклон ковариаты одинаков во всех группах лечения (однородность наклонов регрессии).
регрессии : линейность Предположение 1
Регрессионная связь между зависимой переменной и сопутствующими переменными должна быть линейной.
: однородность дисперсий ошибок Предположение 2
Ошибка представляет собой случайную величину с условным нулевым средним и равными дисперсиями для разных классов лечения и наблюдений.
независимость условий ошибки Допущение 3 :
Ошибки не коррелируют. То есть ковариационная матрица ошибок является диагональной.
Предположение 4: нормальность ошибок [ править ]
Остатки (члены ошибок) должны быть нормально распределены. ~ .
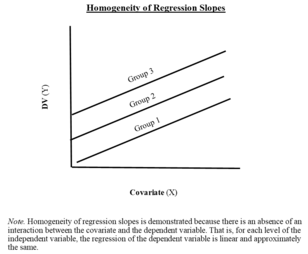
: однородность наклонов регрессии Предположение 5
Наклоны различных линий регрессии должны быть эквивалентными, т. е. линии регрессии должны быть параллельны между группами.
Пятый вопрос, касающийся однородности наклонов регрессии различных методов лечения, особенно важен при оценке приемлемости модели ANCOVA. Также обратите внимание, что нам нужно только, чтобы члены ошибок были нормально распределены. Фактически, как независимая переменная, так и сопутствующие переменные в большинстве случаев не будут иметь нормального распределения.
Проведение ANCOVA [ править ]
Проверка мультиколлинеарности [ править ]
Если CV тесно связано с другим CV (при корреляции 0,5 или более), то DV не будет корректироваться сверх другого CV. Тот или другой следует удалить, поскольку они статистически избыточны.
об однородности дисперсии предположения Проверка
Проверено с помощью теста Левена на равенство дисперсий ошибок.Это наиболее важно после внесения корректировок, но если оно у вас есть до корректировки, оно, скорее всего, будет у вас и после.
об однородности наклонов регрессии Проверьте предположение
Чтобы увидеть, значительно ли взаимодействует CV с категориальным IV, запустите модель ANCOVA, включающую как IV, так и термин взаимодействия CVxIV. Если взаимодействие CVxIV является значительным, ANCOVA не следует выполнять. Вместо этого Грин и Салкинд [5] предложить оценить групповые различия по ДВ на определенных уровнях КВ. Также рассмотрите возможность использования модерируемого регрессионного анализа , рассматривая CV и его взаимодействие как еще один IV. В качестве альтернативы можно использовать посреднический анализ , чтобы определить, учитывает ли CV влияние IV на DV. [ нужна ссылка ] .
Запустить анализ ANCOVA [ править ]
Если взаимодействие CV×IV незначительно, повторите ANCOVA без термина взаимодействия CV×IV. В этом анализе вам необходимо использовать скорректированные средства и скорректированные MSerror. Скорректированные средние значения (также называемые средними наименьшими квадратами, средними LS, оценочными маргинальными средними или EMM) относятся к групповым средним после контроля влияния CV на DV.

Последующие анализы [ править ]
Если имелся значимый главный эффект , то это означает, что существует значительная разница между уровнями одного категориального IV, игнорируя все остальные факторы. [6] Чтобы точно определить, какие уровни существенно отличаются друг от друга, можно использовать те же последующие тесты, что и для ANOVA.При наличии двух и более ИВ возможно существенное взаимодействие , то есть влияние одного ИВ на ДВ меняется в зависимости от уровня другого фактора. Простые основные эффекты можно исследовать, используя те же методы, что и в факторном дисперсионном анализе .
Соображения мощности по
В то время как включение ковариаты в дисперсионный анализ обычно увеличивает статистическую мощность за счет учета некоторой дисперсии зависимой переменной и, таким образом, увеличения отношения дисперсии, объясняемой независимыми переменными, добавление ковариаты в дисперсионный анализ также уменьшает степени свободы . Соответственно, добавление ковариаты, которая учитывает очень небольшую дисперсию зависимой переменной, может фактически снизить мощность.
См. также [ править ]
- MANCOVA (Многомерный ковариационный анализ)
Ссылки [ править ]
- ^ Кеппель, Г. (1991). Дизайн и анализ: Справочник исследователя (3-е изд.). Энглвуд Клиффс: Prentice-Hall, Inc.
- ^ Jump up to: а б Монтгомери, Дуглас К. «Планирование и анализ экспериментов» (8-е изд.). Джон Уайли и сыновья, 2012.
- ^ Табачник, Б.Г.; Фиделл, Л.С. (2007). Использование многомерной статистики (5-е изд.). Бостон: Pearson Education.
- ^ Миллер, Джорджия; Чепмен, JP (2001). «Недоразумение анализа ковариации». Журнал аномальной психологии . 110 (1): 40–48. дои : 10.1037/0021-843X.110.1.40 . ПМИД 11261398 .
- ^ Грин, С.Б., и Салкинд, Нью-Джерси (2011). Использование SPSS для Windows и Macintosh: анализ и понимание данных (6-е изд.). Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл.
- ^ Хауэлл, округ Колумбия (2009) Статистические методы психологии (7-е изд.). Бельмонт: Сенгедж Уодсворт.
Внешние ссылки [ править ]
- Примеры всех моделей ANOVA и ANCOVA с тремя факторами обработки, включая рандомизированный блок, разделенный график, повторные измерения и латинские квадраты, а также их анализ в R (Университет Саутгемптона)
- Односторонний анализ ковариации для независимых выборок
- Для чего используется ковариационный анализ?
- Использование ковариат в рандомизированных контролируемых исследованиях GJP Van Breukelen и KRA Van Dijk (2007).











