Стратифицированная выборка

В статистике , стратифицированная выборка представляет собой метод выборки из совокупности которую можно разделить на подгруппы .

Пример стратифицированной выборки

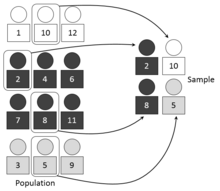
В статистических обследованиях , когда субпопуляции в общей совокупности различаются, может быть полезно выбирать каждую субпопуляцию ( страту ) независимо.

Стратификация – это процесс разделения членов совокупности на однородные подгруппы перед выборкой. Страты должны определять часть населения. То есть оно должно быть коллективно исчерпывающим и взаимоисключающим : каждый элемент совокупности должен быть отнесен к одному и только одному слою. Затем простая случайная выборка внутри каждой страты применяется . Цель состоит в том, чтобы повысить точность выборки за счет уменьшения ошибки выборки . Он может дать средневзвешенное значение , которое имеет меньшую изменчивость, чем среднее арифметическое простой случайной выборки населения.

В вычислительной статистике стратифицированная выборка — это метод уменьшения дисперсии , когда методы Монте-Карло используются для оценки статистики населения на основе известной совокупности.

Пример

Предположим, что нам нужно оценить среднее количество голосов за каждого кандидата на выборах. Предположим, что в стране есть 3 города: в городе А работает 1 миллион фабричных рабочих, в городе Б — 2 миллиона офисных работников, а в городе С — 3 миллиона пенсионеров. Мы можем выбрать случайную выборку размером 60 человек по всему населению, но есть некоторая вероятность того, что полученная случайная выборка будет плохо сбалансирована по этим городам и, следовательно, будет необъективной, что приведет к значительной ошибке в оценке (когда интересующий результат имеет различное распределение по интересующему параметру между городами). Вместо этого, если мы решим взять случайную выборку из 10, 20 и 30 человек из городов A, B и C соответственно, тогда мы сможем получить меньшую ошибку в оценке для того же общего размера выборки. Этот метод обычно используется, когда популяция не является однородной группой.

выборки

1. При пропорциональном распределении в каждой страте используется доля выборки , пропорциональная общей численности населения. Например, если популяция состоит из n особей, m из которых мужчины и f женщин (и где m + f = n ), то относительный размер двух выборок ( x ₁ = m / n мужчин, x ₂ = б / н самки) должны отражать эту пропорцию.
2. Оптимальное распределение (или непропорциональное распределение ). Доля выборки каждой страты пропорциональна как пропорции (как указано выше), так и стандартному отклонению распределения переменной. Более крупные выборки отбираются в стратах с наибольшей изменчивостью, чтобы обеспечить минимально возможную общую дисперсию выборки.

Реальным примером использования стратифицированной выборки может служить политический опрос . Если респондентам необходимо отразить разнообразие населения, исследователь специально постарается включить представителей различных групп меньшинств, таких как раса или религия, на основе их пропорциональности к общей численности населения, как упоминалось выше. Таким образом, стратифицированное обследование может считаться более репрезентативным для населения, чем обследование простой случайной выборки или систематической выборки . Как среднее значение, так и дисперсию можно скорректировать с учетом непропорциональных затрат на выборку, используя стратифицированные размеры выборки .

Преимущества

Причины использования стратифицированной выборки вместо простой случайной выборки включают:

1. Если измерения внутри слоев имеют более низкое стандартное отклонение (по сравнению с общим стандартным отклонением в совокупности), стратификация дает меньшую ошибку в оценке.
2. Для многих приложений измерения становятся более управляемыми и/или более дешевыми, когда совокупность группируется в слои.
3. Когда желательно иметь оценки параметров совокупности для групп внутри совокупности, стратифицированная выборка подтверждает, что у нас достаточно выборок из интересующих слоев.

Если плотность населения сильно варьируется внутри региона, стратифицированная выборка обеспечит возможность получения оценок с одинаковой точностью в разных частях региона и возможность проведения сравнений субрегионов с одинаковой статистической достоверностью . Например, в Онтарио при обследовании, проводимом по всей провинции, может использоваться более крупная доля выборки на менее населенном севере, поскольку неравенство в населении между севером и югом настолько велико, что доля выборки, основанная на выборке по провинции в целом, может привести к сбор лишь небольшого количества данных с севера.

Недостатки

Стратифицированная выборка бесполезна, когда совокупность нельзя полностью разделить на непересекающиеся подгруппы.Было бы неправильным применением этого метода делать размеры выборки подгрупп пропорциональными объему данных, доступных от подгрупп, вместо того, чтобы масштабировать размеры выборки до размеров подгрупп (или их дисперсий, если известно, что они значительно различаются - например, с помощью F-критерия). ). Данные, представляющие каждую подгруппу, считаются одинаково важными, если предполагаемые различия между ними требуют стратифицированной выборки. Если дисперсии подгрупп значительно различаются и данные необходимо стратифицировать по дисперсии, невозможно одновременно сделать размер выборки каждой подгруппы пропорциональным размеру подгруппы в общей совокупности. Об эффективном способе распределения ресурсов выборки между группами, которые различаются по своим средствам, дисперсии и затратам, см. «Оптимальное распределение» .Проблема стратифицированной выборки в случае неизвестных априорных значений класса (соотношение субпопуляций во всей совокупности) может оказать пагубное влияние на эффективность любого анализа набора данных, например классификации. В этом отношении можно использовать минимаксный коэффициент выборки, чтобы сделать набор данных устойчивым к неопределенности в базовом процессе генерации данных.

Объединение подслоев для обеспечения адекватного количества может привести к парадоксу Симпсона , когда тенденции, существующие в разных группах данных, исчезают или даже меняют направление при объединении групп.

и

Среднее значение и дисперсия стратифицированной случайной выборки определяются по формуле:

${\bar {x}}={\frac {1}{N}}\sum _{h=1}^{L}N_{h}{\bar {x}}_{h}$

$s_{\bar {x}}^{2}=\sum _{h=1}^{L}\left({\frac {N_{h}}{N}}\right)^{2}\left({\frac {N_{h}-n_{h}}{N_{h}-1}}\right){\frac {s_{h}^{2}}{n_{h}}}$

где

$L={}$количество слоев

$N={}$сумма всех размеров страты

$N_{h}={}$размер слоя $h$

${\bar {x}}_{h}={}$выборочное среднее страты $h$

$n_{h}={}$количество наблюдений в страте $h$

$s_{h}={}$выборочное стандартное отклонение страты $h$

Обратите внимание, что термин $(N_{h}-n_{h})/(N_{h}-1)$, что равно $1-{\frac {n_{h}-1}{N_{h}-1}}$, представляет собой конечную популяционную поправку и $N_{h}$ должны быть выражены в «единицах выборки». Вышеизложенная поправка на конечную численность дает:

$s_{\bar {x}}^{2}=\sum _{h=1}^{L}\left({\frac {N_{h}}{N}}\right)^{2}{\frac {s_{h}^{2}}{n_{h}}}$

где $w_{h}=N_{h}/N$ это вес населения слоя $h$.

Распределение размера выборки

При использовании стратегии пропорционального распределения размер выборки в каждой страте определяется пропорционально размеру страты. Предположим, что в компании есть следующий персонал:

• мужской, полная занятость: 90
• мужчины, неполная занятость: 18
• женщины, полная занятость: 9
• женщины, неполная занятость: 63
• всего: 180

и нас просят взять выборку из 40 сотрудников, стратифицированных по вышеуказанным категориям.

Первым шагом является вычисление процентной доли каждой группы от общей суммы.

• % мужчин, полный рабочий день = 90 ÷ 180 = 50 %
• % мужчин, неполный рабочий день = 18 ÷ 180 = 10%
• % женщин, полная занятость = 9 ÷ 180 = 5%
• % женщин, неполный рабочий день = 63 ÷ 180 = 35%

Это говорит нам о том, что из нашей выборки из 40 человек

• 50% (20 человек) должны быть мужчинами, работающими полный рабочий день.
• 10% (4 человека) должны быть мужчины, работающие неполный рабочий день.
• 5% (2 человека) должны быть женщинами, работающими полный рабочий день.
• 35% (14 человек) должны быть женщины, работающие неполный рабочий день.

Еще один простой способ без необходимости рассчитывать процент — это умножить размер каждой группы на размер выборки и разделить на общую численность населения (численность всего персонала):

• мужской, очная = 90 × (40 ÷ 180) = 20
• мужской, неполный рабочий день = 18 × (40 ÷ 180) = 4
• женщины, очная = 9 × (40 ÷ 180) = 2
• женщины, неполный рабочий день = 63 × (40 ÷ 180) = 14

См. также

• Опрос общественного мнения
• Многоступенчатый отбор проб
• Статистический бенчмаркинг
• Размер стратифицированной выборки
• Стратификация (клинические исследования)

Дальнейшее чтение

• Сярндал, Карл-Эрик; и др. (2003). «Стратифицированная выборка». Выборка опроса с помощью модели . Нью-Йорк: Спрингер. стр. 100–109. ISBN  0-387-40620-4 .