Максимальная апостериорная оценка

В байесовской статистике максимальная апостериорной вероятности ( MAP ) оценка — это оценка неизвестной величины, которая равна моде апостериорного распределения . MAP можно использовать для получения точечной оценки ненаблюдаемой величины на основе эмпирических данных. Он тесно связан с методом оценки максимального правдоподобия (ML), но использует расширенную цель оптимизации , которая включает в себя априорное распределение (которое количественно определяет дополнительную информацию, доступную благодаря предшествующим знаниям о связанном событии) по величине, которую необходимо оценить. Таким образом, оценку MAP можно рассматривать как регуляризацию оценки максимального правдоподобия.

Описание

Предположим, что мы хотим оценить ненаблюдаемый параметр популяции. $\theta$ на основе наблюдений $x$. Позволять $f$ быть выборочным распределением $x$, так что $f(x\mid \theta )$ это вероятность $x$ когда базовый параметр совокупности равен $\theta$. Тогда функция:

$\theta \mapsto f(x\mid \theta )\!$

известна как функция правдоподобия и оценка:

${\hat {\theta }}_{\mathrm {MLE} }(x)={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )\!$

это оценка максимального правдоподобия $\theta$.

Теперь предположим, что априорное распределение $g$ над $\theta$ существует. Это позволяет нам лечить $\theta$ как случайная величина, как в байесовской статистике . Мы можем вычислить апостериорное распределение $\theta$ используя теорему Байеса :

$\theta \mapsto f(\theta \mid x)={\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}\!$

где $g$ — функция плотности $\theta$, $\Theta$ является областью $g$.

Затем метод максимальной апостериорной оценки оценивает $\theta$ как мода апостериорного распределения этой случайной величины:

${\begin{aligned}{\hat {\theta }}_{\mathrm {MAP} }(x)&={\underset {\theta }{\operatorname {arg\,max} }}\ f(\theta \mid x)\\&={\underset {\theta }{\operatorname {arg\,max} }}\ {\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}\\&={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )\,g(\theta ).\end{aligned}}\!$

Знаменатель апостериорного распределения (так называемое предельное правдоподобие ) всегда положителен и не зависит от $\theta$ и поэтому не играет никакой роли в оптимизации. Обратите внимание, что оценка MAP $\theta$ совпадает с оценкой ML, когда априорная $g$ является однородным (т.е. $g$ является постоянной функцией ).

Когда функция потерь имеет вид

$L(\theta ,a)={\begin{cases}0,&{\text{if }}|a-\theta |<c,\\1,&{\text{otherwise}},\\\end{cases}}$

как $c$ стремится к 0, оценка Байеса приближается к оценке MAP при условии, что распределение $\theta$ он квазивогнутый. Но обычно оценка MAP не является оценкой Байеса, если только $\theta$ является дискретным .

Вычисление

Оценки MAP можно рассчитать несколькими способами:

1. Аналитически, когда мода(ы) апостериорного распределения может быть задана в замкнутой форме . Это тот случай, когда сопряженные априорные значения . используются
2. С помощью численной оптимизации, такой как метод сопряженных градиентов или метод Ньютона . Обычно для этого требуются первые или вторые производные , которые необходимо оценить аналитически или численно.
3. Через модификацию алгоритма максимизации ожидания . Для этого не требуются производные от апостериорной плотности.
4. Методом Монте-Карло с имитацией отжига.

Ограничения

Хотя для оценки MAP требуются только мягкие условия, чтобы она была предельным случаем оценки Байеса (при функции потерь 0–1), в целом он не очень репрезентативен для байесовских методов. Это связано с тем, что оценки MAP являются точечными оценками, тогда как байесовские методы характеризуются использованием распределений для суммирования данных и вывода выводов: таким образом, байесовские методы имеют тенденцию вместо этого сообщать апостериорное среднее или медиану вместе с достоверными интервалами . Это связано как с тем, что эти оценки оптимальны при потерях с квадратичной и линейной ошибкой соответственно (которые более репрезентативны для типичных функций потерь ), так и с тем, что для непрерывного апостериорного распределения не существует функции потерь, которая предполагает, что MAP является оптимальной точечной оценкой. Кроме того, апостериорное распределение часто может не иметь простой аналитической формы: в этом случае распределение можно смоделировать с использованием методов Монте-Карло для цепей Маркова , а оптимизация для нахождения его режима (мод) может быть затруднена или невозможна.

Пример плотности бимодального распределения , при котором высшая мода не характерна для большей части распределения.

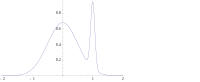
Во многих типах моделей, таких как смешанные модели , задняя часть может быть мультимодальной . В таком случае обычно рекомендуется выбирать самый высокий режим: это не всегда осуществимо ( глобальная оптимизация является сложной проблемой), а в некоторых случаях даже невозможно (например, когда возникают проблемы с идентификацией ). Более того, высшая мода может быть нехарактерна для большинства задних.

Наконец, в отличие от оценок ML, оценка MAP не является инвариантной при перепараметризации. Переход от одной параметризации к другой предполагает введение якобиана , влияющего на расположение максимума.

В качестве примера разницы между упомянутыми выше оценками Байеса (оценками среднего и медианы) и использованием оценки MAP рассмотрим случай, когда необходимо классифицировать входные данные. $x$ как положительные или отрицательные (например, кредиты как рискованные или безопасные). Предположим, что существует всего три возможных гипотезы о правильном методе классификации. $h_{1}$, $h_{2}$ и $h_{3}$ с задними 0,4, 0,3 и 0,3 соответственно. Предположим, что дан новый экземпляр, $x$, $h_{1}$ классифицирует его как положительный, тогда как два других классифицируют его как отрицательный. Использование оценки MAP для правильного классификатора $h_{1}$, $x$ классифицируется как положительный, тогда как оценки Байеса усредняют все гипотезы и классифицируют $x$ как отрицательный.

Пример

Предположим, что нам дана последовательность $(x_{1},\dots ,x_{n})$ МИР ​ $N(\mu ,\sigma _{v}^{2})$ случайные величины и априорное распределение $\mu$ дается $N(\mu _{0},\sigma _{m}^{2})$. Мы хотим найти оценку MAP $\mu$. Обратите внимание, что нормальное распределение является своим собственным сопряженным априором , поэтому мы сможем найти решение в замкнутой форме аналитически.

Тогда функция, которую необходимо максимизировать, определяется выражением

$f(\mu )f(x\mid \mu )=\pi (\mu )L(\mu )={\frac {1}{{\sqrt {2\pi }}\sigma _{m}}}\exp \left(-{\frac {1}{2}}\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}\right)\prod _{j=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma _{v}}}\exp \left(-{\frac {1}{2}}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}\right),$

что эквивалентно минимизации следующей функции $\mu$:

$\sum _{j=1}^{n}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}+\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}.$

Таким образом, мы видим, что оценка MAP для µ имеет вид

${\hat {\mu }}_{\mathrm {MAP} }={\frac {\sigma _{m}^{2}\,n}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\left({\frac {1}{n}}\sum _{j=1}^{n}x_{j}\right)+{\frac {\sigma _{v}^{2}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\,\mu _{0}={\frac {\sigma _{m}^{2}\left(\sum _{j=1}^{n}x_{j}\right)+\sigma _{v}^{2}\,\mu _{0}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}.$

которое оказывается линейной интерполяцией между априорным средним значением и выборочным средним, взвешенным по их соответствующим ковариациям.

Случай $\sigma _{m}\to \infty$ называется неинформативным априором и приводит к неправильному распределению вероятностей ; в этом случае ${\hat {\mu }}_{\mathrm {MAP} }\to {\hat {\mu }}_{\mathrm {MLE} }.$

Ссылки

• ДеГрут, М. (1970). Оптимальные статистические решения . МакГроу-Хилл. ISBN  0-07-016242-5 .
• Соренсон, Гарольд В. (1980). Оценка параметров: принципы и проблемы . Марсель Деккер. ISBN  0-8247-6987-2 .
• Хальд, Андерс (2007). «Вывод Гаусса нормального распределения и метод наименьших квадратов, 1809 г.». История параметрического статистического вывода от Бернулли до Фишера, 1713–1935 гг . Нью-Йорк: Спрингер. стр. 55–61. ISBN  978-0-387-46409-1 .