Сплайн многомерной адаптивной регрессии
В статистике многомерные адаптивные регрессионные сплайны ( MARS ) — это форма регрессионного анализа, введенная Джеромом Х. Фридманом в 1991 году. [1] Это метод непараметрической регрессии , который можно рассматривать как расширение линейных моделей , которое автоматически моделирует нелинейности и взаимодействия между переменными.
Термин «MARS» является торговой маркой и лицензирован компанией Salford Systems. Во избежание нарушений прав на товарные знаки многие реализации MARS с открытым исходным кодом называются «Земля». [2] [3]
Основы [ править ]
В этом разделе MARS представлен на нескольких примерах. Мы начинаем с набора данных: матрицы входных переменных x и вектора наблюдаемых ответов y с ответом для каждой строки в x . Например, данные могут быть:
| х | и |
|---|---|
| 10.5 | 16.4 |
| 10.7 | 18.8 |
| 10.8 | 19.7 |
| ... | ... |
| 20.6 | 77.0 |
Здесь имеется только одна независимая переменная , поэтому матрица x представляет собой всего лишь один столбец. Учитывая эти измерения, мы хотели бы построить модель, которая предсказывает ожидаемый y для данного x .
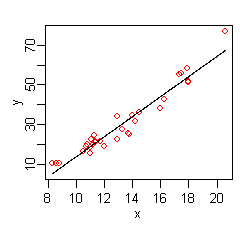
Линейная модель для приведенных выше данных:
Шляпа на указывает на то, что оценивается по данным. На рисунке справа показан график этой функции: линия, дающая предсказанное по сравнению с x , при этом исходные значения y показаны красными точками.
Данные в крайних значениях x указывают на то, что взаимосвязь между y и x может быть нелинейной (посмотрите на красные точки относительно линии регрессии при низких и высоких значениях x ). Таким образом, мы обращаемся к MARS для автоматического построения модели с учетом нелинейностей. Программное обеспечение MARS строит модель по заданным x и y следующим образом:
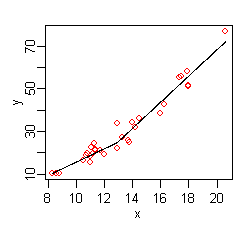
На рисунке справа показан график этой функции: предсказанное по сравнению с x , при этом исходные значения y снова показаны красными точками. Прогнозируемый ответ теперь лучше соответствует исходным значениям y .
MARS автоматически произвел излом в предсказанном y, чтобы принять во внимание нелинейность. Излом создается шарнирными функциями . Шарнирные функции — это выражения, начинающиеся с (где является если , еще ). Более подробно функции шарнира описаны ниже.
В этом простом примере мы можем легко увидеть на графике, что y имеет нелинейную связь с x (и, возможно, могли бы догадаться, что y зависит от квадрата x ). Однако, как правило, будет несколько независимых переменных , и взаимосвязь между y и этими переменными будет неясной и ее будет трудно увидеть на графике. Мы можем использовать MARS, чтобы обнаружить эту нелинейную зависимость.
Пример выражения MARS с несколькими переменными:
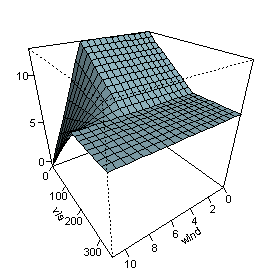
Это выражение моделирует загрязнение воздуха (уровень озона) как функцию температуры и некоторых других переменных. Обратите внимание, что последний член формулы (в последней строке) включает в себя взаимодействие между и .
На рисунке справа изображен прогнозируемый как и варьироваться, при этом остальные переменные фиксируются на своих медианных значениях. На рисунке показано, что ветер не влияет на уровень озона, если видимость низкая. Мы видим, что MARS может строить довольно гибкие поверхности регрессии, комбинируя шарнирные функции.
Для получения приведенного выше выражения процедура построения модели MARS автоматически выбирает, какие переменные использовать (некоторые переменные важны, другие нет), положения изломов в шарнирных функциях и способ объединения шарнирных функций.
Модель MARS [ править ]
MARS строит модели формы
Модель представляет собой взвешенную сумму базисных функций. .Каждый является постоянным коэффициентом.Например, каждая строка в приведенной выше формуле для озона представляет собой одну базисную функцию.умножается на его коэффициент.
Каждая базисная функция принимает одну из следующих трех форм:
1) константа 1. Такой термин есть только один — перехват.В приведенной выше формуле для озона член-член равен 5,2.
2) шарнирная функция. Шарнирная функция имеет вид или . MARS автоматически выбирает переменные и значения этих переменных для узлов шарнирных функций. Примеры таких базисных функций можно увидеть в трех средних строках формулы озона.
3) произведение двух и более шарнирных функций.Эти базисные функции могут моделировать взаимодействие между двумя или более переменными.Примером может служить последняя строка формулы озона.
Функции шарнира [ править ]
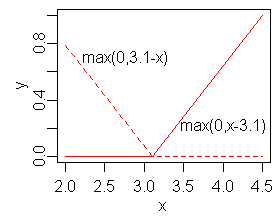
Ключевой частью моделей MARS являются шарнирные функции, имеющие вид
или
где является константой, называемой узлом .На рисунке справа показана зеркальная пара шарнирных функций с узлом 3,1.
Функция шарнира равна нулю для части своего диапазона, поэтому ее можно использовать для разделения данных на непересекающиеся области, каждую из которых можно обрабатывать независимо. Так, например, зеркальная пара шарнирных функций в выражении
создает кусочно -линейный график, показанный для простой модели MARS в предыдущем разделе.
Можно предположить, что из шарнирных функций можно образовать только кусочно-линейные функции, но шарнирные функции можно умножать вместе, образуя нелинейные функции.
Шарнирные функции также называются рампы , хоккейной клюшки или выпрямителя функциями . Вместо В обозначениях, используемых в этой статье, шарнирные функции часто представляются как где значит принять положительную сторону.
Процесс построения модели [ править ]
MARS строит модель в два этапа:пас вперед и назад.Этот двухэтапный подход аналогичен тому, который используется рекурсивное разбиение деревьев.
Пас вперед [ править ]
MARS начинается с модели, состоящей только из члена-члена.(что является средним значением ответов).
Затем MARS неоднократно добавляет в модель базисную функцию попарно. ошибки суммы квадратов На каждом шаге он находит пару базисных функций, которая дает максимальное уменьшение остаточной (это жадный алгоритм ). Две базисные функции в паре идентичны, за исключением того, что для каждой функции используется разная сторона зеркальной шарнирной функции. Каждая новая базисная функция состоит из члена, уже присутствующего в модели (который, возможно, может быть перехватывающим термином), умноженного на новую шарнирную функцию. Шарнирная функция определяется переменной и узлом, поэтому, чтобы добавить новую базисную функцию, MARS должен выполнить поиск по всем комбинациям следующих элементов:
1) существующие термины (в данном контексте называемые родительскими терминами )
2) все переменные (чтобы выбрать одну для новой базовой функции)
3) все значения каждой переменной (для узла новой шарнирной функции).
Чтобы вычислить коэффициент каждого термина, MARS применяет линейную регрессию по всем терминам.
Этот процесс добавления членов продолжается до тех пор, пока изменение остаточной ошибки не станет слишком малым для продолжения или пока не будет достигнуто максимальное количество членов. Максимальное количество терминов задается пользователем перед началом построения модели.
Поиск на каждом этапе обычно выполняется методом грубой силы , но ключевым аспектом MARS является то, что из-за характера шарнирных функций поиск может выполняться быстро с использованием метода быстрого обновления методом наименьших квадратов. Поиск методом грубой силы можно ускорить, используя эвристику , которая уменьшает количество родительских терминов, рассматриваемых на каждом этапе («Быстрый MARS» [4] ).
Обратный проход [ править ]
Прямой проход обычно не соответствует модели. Чтобы построить модель с лучшей способностью к обобщению, обратный проход сокращает модель, удаляя наименее эффективный член на каждом этапе, пока не будет найдена лучшая подмодель. Подмножества моделей сравниваются с использованием критерия обобщенной перекрестной проверки (GCV), описанного ниже.
Обратный проход имеет преимущество перед прямым проходом: на любом этапе он может выбрать любой термин для удаления, тогда как прямой проход на каждом шаге может видеть только следующую пару терминов.
При прямом проходе термины добавляются парами, но при обратном проходе обычно отбрасывается одна сторона пары, поэтому в окончательной модели термины часто не видны парами. Парный шарнир можно увидеть в уравнении для в первом примере MARS выше; в примере с озоном не сохраняется полных пар.
Обобщенная перекрестная проверка [ править ]
Обратный проход сравнивает производительность различных моделей с использованием обобщенной перекрестной проверки (GCV), второстепенного варианта информационного критерия Акаике , который аппроксимирует показатель перекрестной проверки с исключением одного в особом случае, когда ошибки являются гауссовыми или когда используется функция потерь квадратичной ошибки. GCV был представлен Крэйвеном и Вахбой и расширен Фридманом для MARS; более низкие значения GCV указывают на лучшие модели. Формула для GCV:
- GCV = RSS / ( N · (1 − (эффективное количество параметров) / N ) 2 )
где RSS — остаточная сумма квадратов, измеренная на обучающих данных, а N — количество наблюдений (количество строк в матрице x ).
Эффективное количество параметров определяется как
- (эффективное количество параметров) = (количество марсианских терминов) + (штраф) · ((количество марсианских терминов) − 1 ) / 2
где штраф обычно равен 2 (давая результаты, эквивалентные информационному критерию Акаике ), но может быть увеличен пользователем, если он того пожелает.
Обратите внимание, что
- (количество членов Марса — 1) / 2
— количество узлов шарнирной функции, поэтому формула наказывает добавление узлов. Таким образом, формула GCV корректирует (то есть увеличивает) обучающий RSS, чтобы наказать более сложные модели. Мы наказываем гибкость, потому что слишком гибкие модели будут моделировать конкретную реализацию шума в данных, а не просто систематическую структуру данных.
Ограничения [ править ]
Одно ограничение уже упоминалось: пользовательможно указать максимальное количество терминов в прямом проходе.
На прямой проход можно наложить еще одно ограничение.путем указания максимально допустимой степени взаимодействия.Обычно допускается только одна или две степени взаимодействия.но можно использовать и более высокие степени, когда данные того требуют.Максимальная степень взаимодействия в первом примере MARSвыше — один (т.е. никаких взаимодействий или аддитивной модели ); в примере с озоном это два.
Возможны и другие ограничения на прямой проход.Например, пользователь может указать, что взаимодействие разрешено. только для определенных входных переменных.Такие ограничения могут иметь смысл благодаря знаниямпроцесса, который генерировал данные.
Плюсы и минусы [ править ]
Эта статья , возможно, содержит оригинальные исследования . ( Октябрь 2016 г. ) |
Ни один метод регрессионного моделирования не является лучшим для всех ситуаций.Приведенные ниже рекомендации призваны дать представление о плюсах и минусах MARS. но из правил будут исключения.Полезно сравнить MARS с рекурсивным секционированием , и это сделано ниже.(Рекурсивное разбиение также часто называют деревьями регрессии . деревья решений , или CART ; см . в статье о рекурсивном секционировании подробности ).
- Модели MARS более гибкие, чем модели линейной регрессии .
- Модели MARS просты для понимания и интерпретации. [5] Сравните приведенное выше уравнение концентрации озона, скажем, с внутренностями обученной нейронной сети или случайного леса .
- MARS может обрабатывать как непрерывные, так и категориальные данные . [6] [7] MARS, как правило, лучше, чем рекурсивное секционирование для числовых данных, поскольку шарниры более подходят для числовых переменных, чем кусочно-постоянная сегментация, используемая при рекурсивном секционировании.
- Построение моделей MARS часто требует незначительной подготовки данных или вообще не требует ее. [5] Функции шарнира автоматически разделяют входные данные, поэтому влияние выбросов ограничивается. В этом отношении MARS похож на рекурсивное секционирование , которое также разделяет данные на непересекающиеся области, хотя и использует другой метод.
- MARS (как и рекурсивное секционирование) выполняет автоматический выбор переменных (то есть включает в модель важные переменные и исключает неважные). Однако при выборе может быть некоторая произвольность, особенно при наличии коррелирующих предикторов, и это может повлиять на интерпретируемость. [5]
- Модели MARS, как правило, имеют хороший компромисс между смещением и дисперсией. Модели достаточно гибки, чтобы моделировать нелинейность и переменные взаимодействия (таким образом, модели MARS имеют довольно низкую систематическую ошибку), однако ограниченная форма базисных функций MARS предотвращает слишком большую гибкость (таким образом, модели MARS имеют довольно низкую дисперсию).
- MARS подходит для обработки больших наборов данных, а реализация выполняется очень быстро. Однако рекурсивное секционирование может быть быстрее, чем MARS. [ нужна ссылка ] .
- В моделях MARS, как и в любой непараметрической регрессии, доверительные интервалы параметров и другие проверки модели не могут быть рассчитаны напрямую (в отличие от линейной регрессии моделей перекрестную проверку и связанные с ней методы. ). Вместо этого для проверки модели необходимо использовать
- The
earth,mda, иpolsplineреализации не допускают пропущенных значений в преикторах, но свободные реализации деревьев регрессии (таких какrpartиparty) допускают пропущенные значения, используя метод, называемый суррогатным разделением. - Модели MARS могут делать прогнозы очень быстро, поскольку они требуют только оценки линейной функции предикторов.
- Полученная подобранная функция является непрерывной, в отличие от рекурсивного разделения, которое в некоторых ситуациях может дать более реалистичную модель. (Однако модель не является гладкой или дифференцируемой).
[ править ]
- Обобщенные линейные модели (GLM) можно включить в модели MARS, применив функцию связи после построения модели MARS. Так, например, модели MARS могут включать логистическую регрессию для прогнозирования вероятностей.
- Нелинейная регрессия используется, когда известна основная форма функции, и регрессия используется только для оценки параметров этой функции. MARS, с другой стороны, оценивает сами функции, хотя и с серьезными ограничениями на природу функций. (Эти ограничения необходимы, поскольку обнаружение модели по данным — это обратная задача , которая не является корректной без ограничений на модель.)
- Рекурсивное секционирование (обычно называемое CART). MARS можно рассматривать как обобщение рекурсивного разделения, позволяющее создавать непрерывные модели, которые лучше подходят для числовых данных.
- Обобщенные аддитивные модели . В отличие от MARS, GAM соответствуют гладким лессовым или полиномиальным сплайнам, а не шарнирным функциям, и они не моделируют автоматически взаимодействия переменных. Более плавное соответствие и отсутствие членов регрессии уменьшают дисперсию по сравнению с MARS, но игнорирование взаимодействий переменных может усугубить смещение.
- ЦМАРС . Марс временных рядов — это термин, используемый, когда модели MARS применяются в контексте временных рядов. Обычно в этой настройке предикторами являются значения временных рядов с запаздыванием, приводящие к авторегрессионным сплайновым моделям. Эти модели и расширения, включающие сплайновые модели скользящего среднего, описаны в документе «Моделирование и прогнозирование одномерных временных рядов с использованием TSMARS: исследование авторегрессионных, сезонных и скользящих средних моделей пороговых временных рядов с использованием TSMARS».
- Байесовский MARS (BMARS) использует ту же форму модели, но строит модель с использованием байесовского подхода. Это может привести к различным оптимальным моделям MARS, поскольку подход к построению моделей отличается. Результатом BMARS обычно является ансамбль апостериорных выборок моделей MARS, что позволяет делать вероятностные прогнозы. [8]
См. также [ править ]
- Линейная регрессия
- Локальная регрессия
- Моделирование рациональных функций
- Сегментированная регрессия
- Сплайн-интерполяция
- Сплайн-регрессия
Ссылки [ править ]
- ^ Фридман, Дж. Х. (1991). «Многомерные сплайны адаптивной регрессии». Анналы статистики . 19 (1): 1–67. CiteSeerX 10.1.1.382.970 . дои : 10.1214/aos/1176347963 . JSTOR 2241837 . МР 1091842 . Збл 0765.62064 .
- ^ Земля пакета CRAN
- ^ Земля – сплайны многомерной адаптивной регрессии в Orange (библиотека машинного обучения Python)
- ^ Фридман, Дж. Х. (1993) Fast MARS , Статистический факультет Стэнфордского университета, Технический отчет 110
- ^ Jump up to: а б с Кун, Макс; Джонсон, Кьелл (2013). Прикладное прогнозное моделирование . Нью-Йорк, штат Нью-Йорк: Springer New York. дои : 10.1007/978-1-4614-6849-3 . ISBN 9781461468486 .
- ^ Фридман, Джером Х. (1993). «Оценка функций смешанных порядковых и категориальных переменных с использованием адаптивных сплайнов». У Стефана Моргенталера; Эльвезио Ронкетти; Вернер Стахель (ред.). Новые направления в статистическом анализе данных и их устойчивости . Биркгаузер.
- ^ Фридман, Джером Х. (1 июня 1991 г.). «Оценка функций смешанных порядковых и категориальных переменных с использованием адаптивных сплайнов» . ДТИК . Архивировано из оригинала 11 апреля 2022 года . Проверено 11 апреля 2022 г.
- ^ Денисон, DGT; Маллик, Британская Колумбия; Смит, AFM (1 декабря 1998 г.). «Байесовский МАРС» (PDF) . Статистика и вычисления . 8 (4): 337–346. дои : 10.1023/А:1008824606259 . ISSN 1573-1375 . S2CID 12570055 .
Дальнейшее чтение [ править ]
- Хасти Т., Тибширани Р. и Фридман Дж. Х. (2009) Элементы статистического обучения , 2-е издание. Спрингер, ISBN 978-0-387-84857-0 (есть раздел о МАРСе)
- Фарауэй Дж. (2005) Расширение линейной модели с помощью R , CRC, ISBN 978-1-58488-424-8 (есть пример использования MARS с R)
- Хэпин Чжан и Бертон Х. Сингер (2010) Рекурсивное секционирование и приложения , 2-е издание. Спрингер, ISBN 978-1-4419-6823-4 (есть глава о MARS и обсуждаются некоторые настройки алгоритма)
- Денисон Д.Г.Т., Холмс К.С., Маллик Б.К. и Смит А.Ф.М. (2004) Байесовские методы для нелинейной классификации и регрессии , Уайли, ISBN 978-0-471-49036-4
- Берк Р.А. (2008) Статистическое обучение с точки зрения регрессии , Спрингер, ISBN 978-0-387-77500-5
Внешние ссылки [ править ]
в этой статье Использование внешних ссылок может не соответствовать политике и рекомендациям Википедии . ( Октябрь 2016 г. ) |
Для установки моделей типа MARS доступно несколько бесплатных и коммерческих пакетов программного обеспечения.
- Бесплатное программное обеспечение
- Р -пакеты:
- Код Матлаба:
- ARESLab: набор инструментов адаптивных сплайнов регрессии для Matlab
- Код из книги Байесовские методы нелинейной классификации и регрессии [1] для байесовского МАРС.
- Питон
- Земля – сплайны многомерной адаптивной регрессии
- пи-земля
- pyBASS для байесовского MARS.
- Коммерческое программное обеспечение
- МАРС от Salford Systems. На основе реализации Фридмана.
- STATISTICA Data Miner от StatSoft
- АДАПТИВЕРЕГ от SAS.
- ^ Денисон, DGT; Холмс, CC; Маллик, Британская Колумбия; Смит, AFM (2002). Байесовские методы нелинейной классификации и регрессии . Чичестер, Англия: Уайли. ISBN 978-0-471-49036-4 .





















![{\displaystyle [\pm (x_{i}-c)]_{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4164761539b8c42b6abe93e151683852d9ec043)
![{\displaystyle [\cdot ]_{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0196f79f9c7c8c6a7777ab193018b24c6f4b1a92)