Статистика заказов

Функции плотности вероятности статистики порядка для выборки объемом n = 5 из экспоненциального распределения с параметром единичного масштаба

В статистике статистической выборки равна статистика k-го порядка k ее - му наименьшему значению. Вместе со статистикой рангов статистика порядков является одним из наиболее фундаментальных инструментов непараметрической статистики и вывода .

Важными особыми случаями порядковой статистики являются минимальное и максимальное значение выборки, а также (с некоторыми оговорками, обсуждаемыми ниже) медиана выборки и другие квантили выборки .

При использовании теории вероятностей для анализа статистики порядка случайных выборок из непрерывного распределения используется кумулятивная функция распределения , чтобы свести анализ к случаю статистики порядка равномерного распределения .

Обозначения и примеры

Например, предположим, что наблюдаются или записываются четыре числа, в результате чего получается выборка размером 4. Если значения выборки равны

6, 9, 3, 8,

статистика заказов будет обозначаться

$x_{(1)}=3,\ \ x_{(2)}=6,\ \ x_{(3)}=8,\ \ x_{(4)}=9,\,$

где индекс ( i ), заключенный в круглые скобки, указывает статистику i -го порядка выборки.

Статистика первого порядка (или статистика наименьшего порядка ) всегда является минимумом выборки, то есть

$X_{(1)}=\min\{\,X_{1},\ldots ,X_{n}\,\}$

где, следуя общепринятому соглашению, мы используем прописные буквы для обозначения случайных величин и строчные буквы (как указано выше) для обозначения их фактических наблюдаемых значений.

Аналогично, для выборки размера n статистика n- го порядка (или статистика наибольшего порядка ) является максимальной , то есть

$X_{(n)}=\max\{\,X_{1},\ldots ,X_{n}\,\}.$

Диапазон выборки — это разница между максимальным и минимальным значением. Это функция статистики заказов:

${\rm {Range}}\{\,X_{1},\ldots ,X_{n}\,\}=X_{(n)}-X_{(1)}.$

Аналогичная важная статистика в исследовательском анализе данных , которая просто связана со статистикой порядка, — это выборочный межквартильный размах .

Выборочная медиана может быть или не быть порядковой статистикой, поскольку единственное среднее значение существует только тогда, когда число n наблюдений нечетно . Точнее, если n = 2 m +1 для некоторого целого числа m , то выборочная медиана равна $X_{(m+1)}$ и такова статистика заказов. С другой стороны, когда n = 2 n четно, м и имеются два средних значения, $X_{(m)}$ и $X_{(m+1)}$, а выборочная медиана является некоторой функцией этих двух значений (обычно средней) и, следовательно, не является порядковой статистикой. Подобные замечания применимы ко всем квантилям выборки.

Вероятностный анализ

Учитывая любые случайные величины X ₁ , X ₂ ..., X _n , статистика порядка X ₍₁₎ , X ₍₂₎ , ..., X _{( n )} также является случайными величинами, определяемыми путем сортировки значений ( реализаций ) X в ₁ , ..., X _n порядке возрастания.

Когда случайные величины X ₁ , X ₂ ..., X _n образуют выборку, они независимы и одинаково распределены . Именно этот случай рассматривается ниже. В общем, случайные величины X ₁ , ..., X _n могут возникнуть в результате выборки из более чем одной совокупности. Тогда они независимы , но не обязательно одинаково распределены, а их совместное распределение вероятностей задается теоремой Бапата-Бега .

В дальнейшем мы будем предполагать, что рассматриваемые случайные величины непрерывны , а там, где это удобно, будем также предполагать, что они имеют функцию плотности вероятности (PDF), то есть абсолютно непрерывны . особенности анализа распределений, присваивающих массу точкам (в частности, дискретных распределений В конце обсуждаются ).

Кумулятивная функция распределения статистики заказов

Для случайной выборки, как указано выше, с кумулятивным распределением $F_{X}(x)$, статистика заказов для этой выборки имеет кумулятивное распределение следующим образом: (где r указывает статистику какого порядка):

$F_{X_{(r)}}(x)=\sum _{j=r}^{n}{\binom {n}{j}}[F_{X}(x)]^{j}[1-F_{X}(x)]^{n-j}$

соответствующая функция плотности вероятности может быть получена из этого результата и оказывается равной

$f_{X_{(r)}}(x)={\frac {n!}{(r-1)!(n-r)!}}f_{X}(x)[F_{X}(x)]^{r-1}[1-F_{X}(x)]^{n-r}.$

Более того, есть два особых случая, в которых CDF легко вычислить.

$F_{X_{(n)}}(x)=\operatorname {Prob} (\max\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=[F_{X}(x)]^{n}$

$F_{X_{(1)}}(x)=\operatorname {Prob} (\min\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=1-[1-F_{X}(x)]^{n}$

Что можно получить путем тщательного рассмотрения вероятностей.

статистики

распределения

В этом разделе мы показываем, что порядковая статистика равномерного распределения на единичном интервале имеет маргинальные распределения, принадлежащие семейству бета-распределений . Мы также даем простой метод получения совместного распределения любого количества статистик порядка и, наконец, переводим эти результаты в произвольные непрерывные распределения с помощью cdf .

На протяжении всего этого раздела мы предполагаем, что $X_{1},X_{2},\ldots ,X_{n}$ это случайная выборка, полученная из непрерывного распределения с помощью cdf $F_{X}$. Обозначая $U_{i}=F_{X}(X_{i})$ мы получаем соответствующую случайную выборку $U_{1},\ldots ,U_{n}$ из стандартного равномерного распределения . Обратите внимание, что статистика заказов также удовлетворяет $U_{(i)}=F_{X}(X_{(i)})$.

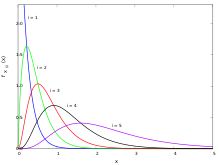
Функция плотности вероятности статистики порядка $U_{(k)}$ равно

$f_{U_{(k)}}(u)={n! \over (k-1)!(n-k)!}u^{k-1}(1-u)^{n-k}$

то есть статистика k -го порядка равномерного распределения представляет собой случайную величину с бета-распределением .

$U_{(k)}\sim \operatorname {Beta} (k,n+1\mathbf {-} k).$

Доказательство этих утверждений состоит в следующем. Для $U_{(k)}$ Чтобы находиться между u и u + du , необходимо, чтобы ровно k − 1 элементов выборки были меньше u и чтобы хотя бы один находился между u и u + d u . Вероятность того, что в этом последнем интервале окажется более одного, уже равна $O(du^{2})$, поэтому нам нужно вычислить вероятность того, что ровно k − 1, 1 и n − k наблюдений попадут в интервалы $(0,u)$, $(u,u+du)$ и $(u+du,1)$ соответственно. см. Полиномиальное распределение Это равно ( подробнее )

${n! \over (k-1)!(n-k)!}u^{k-1}\cdot du\cdot (1-u-du)^{n-k}$

и результат следующий.

Среднее значение этого распределения равно k /( n + 1).

Совместное распределение статистики заказов равномерного распределения

Аналогично, для i < j , что совместная функция плотности вероятности статистики двух порядков U _{( i )} < U _{( j )} можно показать равна

$f_{U_{(i)},U_{(j)}}(u,v)=n!{u^{i-1} \over (i-1)!}{(v-u)^{j-i-1} \over (j-i-1)!}{(1-v)^{n-j} \over (n-j)!}$

что (с точностью до членов более высокого порядка, чем $O(du\,dv)$) вероятность того, что i − 1, 1, j − 1 − i , 1 и n − j элементов выборки попадают в интервалы $(0,u)$, $(u,u+du)$, $(u+du,v)$, $(v,v+dv)$, $(v+dv,1)$ соответственно.

Совершенно аналогичным образом можно рассуждать и о выводе совместных распределений более высокого порядка. Возможно, это удивительно, но совместная плотность статистики n-го порядка оказывается постоянной :

$f_{U_{(1)},U_{(2)},\ldots ,U_{(n)}}(u_{1},u_{2},\ldots ,u_{n})=n!.$

Один из способов понять это состоит в том, что неупорядоченный образец действительно имеет постоянную плотность, равную 1, и что существует n ! разные перестановки выборки, соответствующие одной и той же последовательности статистики порядка. Это связано с тем, что 1/ n ! это объем региона $0<u_{1}<\cdots <u_{n}<1$. Это связано также с другой особенностью порядковой статистики однородных случайных величин: из BRS-неравенства следует , что максимальное ожидаемое число однородных U(0,1] случайных величин, которое можно выбрать из выборки размера n с суммой не превышающий $0<s<n/2$ ограничено сверху ${\sqrt {2sn}}$, который, таким образом, инвариантен на множестве всех $s,n$ с постоянным продуктом $sn$.

Используя приведенные выше формулы, можно вывести распределение диапазона статистики порядка, то есть распределение $U_{(n)}-U_{(1)}$, то есть максимум минус минимум. В более общем смысле для $n\geq k>j\geq 1$, $U_{(k)}-U_{(j)}$ также есть бета-дистрибутив:

$$U_{(k)}-U_{(j)}\sim \operatorname {Beta} (k-j,n-(k-j)+1)$$

Из этих формул мы можем вывести ковариацию между статистиками двух порядков:

$$\operatorname {Cov} (U_{(k)},U_{(j)})={\frac {j(n-k+1)}{(n+1)^{2}(n+2)}}$$

Формула следует из того, что

$$\operatorname {Var} (U_{(k)}-U_{(j)})=\operatorname {Var} (U_{(k)})+\operatorname {Var} (U_{(j)})-2\cdot \operatorname {Cov} (U_{(k)},U_{(j)})={\frac {k(n-k+1)}{(n+1)^{2}(n+2)}}+{\frac {j(n-j+1)}{(n+1)^{2}(n+2)}}-2\cdot \operatorname {Cov} (U_{(k)},U_{(j)})$$

и сравнивая это с

$$\operatorname {Var} (U)={\frac {(k-j)(n-(k-j)+1)}{(n+1)^{2}(n+2)}}$$

где $U\sim \operatorname {Beta} (k-j,n-(k-j)+1)$, что является фактическим распределением разницы.

заказов, полученная из

Для $X_{1},X_{2},..,X_{n}$ случайная выборка размером n из экспоненциального распределения с параметром λ , статистика порядка X _{( i )} для i = 1,2,3, ..., n имеет распределение

$X_{(i)}{\stackrel {d}{=}}{\frac {1}{\lambda }}\left(\sum _{j=1}^{i}{\frac {Z_{j}}{n-j+1}}\right)$

где Z _j — стандартные экспоненциальные случайные величины iid (т.е. с параметром скорости 1). Этот результат был впервые опубликован Альфредом Реньи .

взятая из дистрибутива

Преобразование Лапласа статистики порядка можно выбрать из распределения Эрланга с помощью метода подсчета путей. .

Совместное распределение статистики заказов абсолютно непрерывного распределения

Если F _X , абсолютно непрерывен он имеет такую ​​плотность, что $dF_{X}(x)=f_{X}(x)\,dx$, и мы можем использовать замены

$u=F_{X}(x)$

и

$du=f_{X}(x)\,dx$

чтобы получить следующие функции плотности вероятности для статистики порядка выборки размера n, взятой из распределения X :

$f_{X_{(k)}}(x)={\frac {n!}{(k-1)!(n-k)!}}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{n-k}f_{X}(x)$

$f_{X_{(j)},X_{(k)}}(x,y)={\frac {n!}{(j-1)!(k-j-1)!(n-k)!}}[F_{X}(x)]^{j-1}[F_{X}(y)-F_{X}(x)]^{k-1-j}[1-F_{X}(y)]^{n-k}f_{X}(x)f_{X}(y)$ где $x\leq y$

$f_{X_{(1)},\ldots ,X_{(n)}}(x_{1},\ldots ,x_{n})=n!f_{X}(x_{1})\cdots f_{X}(x_{n})$ где $x_{1}\leq x_{2}\leq \dots \leq x_{n}.$

: доверительные интервалы

Интересный вопрос заключается в том, насколько хорошо статистика порядка выполняет функцию оценки квантилей основного распределения.

Пример небольшого размера выборки

Самый простой случай, который следует рассмотреть, — это то, насколько хорошо медиана выборки оценивает медиану совокупности.

В качестве примера рассмотрим случайную выборку размером 6. В этом случае медиана выборки обычно определяется как середина интервала, ограниченного статистикой 3-го и 4-го порядка. Однако из предыдущего обсуждения мы знаем, что вероятность того, что этот интервал действительно содержит медиану совокупности, равна

${6 \choose 3}(1/2)^{6}={5 \over 16}\approx 31\%.$

Хотя выборочная медиана, вероятно, является одной из лучших точечных оценок медианы совокупности, не зависящих от распределения, этот пример иллюстрирует то, что она не особенно хороша в абсолютном выражении. В данном конкретном случае лучшим доверительным интервалом для медианы является интервал, ограниченный статистикой 2-го и 5-го порядка, который содержит медиану совокупности с вероятностью

$\left[{6 \choose 2}+{6 \choose 3}+{6 \choose 4}\right](1/2)^{6}={25 \over 32}\approx 78\%.$

При таком небольшом размере выборки, если кто-то хочет иметь уверенность не менее 95%, приходится говорить, что медиана находится между минимумом и максимумом из 6 наблюдений с вероятностью 31/32 или примерно 97%. Размер 6 фактически представляет собой наименьший размер выборки, при котором интервал, определяемый минимумом и максимумом, составляет как минимум 95% доверительный интервал для медианы генеральной совокупности.

Большие размеры выборки

Для равномерного распределения, когда n стремится к бесконечности, p ^й Квантиль выборки асимптотически нормально распределен , поскольку он аппроксимируется выражением

$U_{(\lceil np\rceil )}\sim AN\left(p,{\frac {p(1-p)}{n}}\right).$

Для общего распределения F с непрерывной ненулевой плотностью в F  ⁻¹ ( p ), применяется аналогичная асимптотическая нормальность:

$X_{(\lceil np\rceil )}\sim AN\left(F^{-1}(p),{\frac {p(1-p)}{n[f(F^{-1}(p))]^{2}}}\right)$

где f — функция плотности , а F  ⁻¹ — функция квантиля, с F. связанная Одним из первых, кто упомянул и доказал этот результат, был Фредерик Мостеллер в своей основополагающей статье 1946 года. Дальнейшие исследования привели в 1960-х годах к представлению Бахадура , которое предоставляет информацию о границах ошибок. Сходимость к нормальному распределению также имеет место в более сильном смысле, например, сходимость по относительной энтропии или КЛ-дивергенция .

Интересное наблюдение можно сделать в случае, когда распределение симметрично, а медиана населения равна среднему значению населения. В этом случае выборочное среднее по центральной предельной теореме также асимптотически нормально распределено, но с дисперсией σ ² /n вместо этого. Этот асимптотический анализ предполагает, что среднее значение превосходит медиану в случаях низкого эксцесса , и наоборот. Например, медиана обеспечивает лучшие доверительные интервалы для распределения Лапласа , в то время как среднее работает лучше для X , которые имеют нормальное распределение.

Доказательство

Можно показать, что

$B(k,n+1-k)\ {\stackrel {\mathrm {d} }{=}}\ {\frac {X}{X+Y}},$

где

$X=\sum _{i=1}^{k}Z_{i},\quad Y=\sum _{i=k+1}^{n+1}Z_{i},$

где Z _i являются независимыми одинаково распределенными экспоненциальными случайными величинами с частотой 1. Поскольку X / n и Y / n асимптотически нормально распределяются с помощью CLT, наши результаты получены на основе применения дельта-метода .

Непараметрическая оценка

Моменты распределения статистики первого порядка можно использовать для разработки непараметрической оценки плотности. Предположим, мы хотим оценить плотность $f_{X}$ в точку $x^{*}$. Рассмотрим случайные величины $Y_{i}=|X_{i}-x^{*}|$, которые являются iid с функцией распределения $g_{Y}(y)=f_{X}(y+x^{*})+f_{X}(x^{*}-y)$. В частности, $f_{X}(x^{*})={\frac {g_{Y}(0)}{2}}$.

Ожидаемое значение статистики первого порядка $Y_{(1)}$ дали образец $N$ общая доходность наблюдений,

$E(Y_{(1)})={\frac {1}{(N+1)g(0)}}+{\frac {1}{(N+1)(N+2)}}\int _{0}^{1}Q''(z)\delta _{N+1}(z)\,dz$

где $Q$ - функция квантиля, связанная с распределением $g_{Y}$, и $\delta _{N}(z)=(N+1)(1-z)^{N}$. Это уравнение в сочетании с методом складного ножа становится основой для следующего алгоритма оценки плотности:

  Input: A sample of $N$ observations. $\{x_{\ell }\}_{\ell =1}^{M}$ points of density evaluation. Tuning parameter $a\in (0,1)$ (usually 1/3).
  Output: $\{{\hat {f}}_{\ell }\}_{\ell =1}^{M}$ estimated density at the points of evaluation.

  1: Set $m_{N}=\operatorname {round} (N^{1-a})$
  2: Set $s_{N}={\frac {N}{m_{N}}}$
  3: Create an $s_{N}\times m_{N}$ matrix $M_{ij}$ which holds $m_{N}$ subsets with $s_{N}$ observations each.
  4: Create a vector ${\hat {f}}$ to hold the density evaluations.
  5: for $\ell =1\to M$ do
  6:     for $k=1\to m_{N}$ do
  7:         Find the nearest distance $d_{\ell k}$ to the current point $x_{\ell }$ within the $k$th subset
  8:      end for
  9:      Compute the subset average of distances to $x_{\ell }:d_{\ell }=\sum _{k=1}^{m_{N}}{\frac {d_{\ell k}}{m_{N}}}$
 10:      Compute the density estimate at $x_{\ell }:{\hat {f}}_{\ell }={\frac {1}{2(1+s_{N})d_{\ell }}}$
 11:  end for
 12: return ${\hat {f}}$

В отличие от параметров настройки на основе полосы пропускания/длины для подходов на основе гистограммы и ядра , параметром настройки для оценки плотности на основе статистики порядка является размер подмножеств выборки. Такая оценка более надежна, чем подходы, основанные на гистограмме и ядре, например, такие плотности, как распределение Коши (в котором отсутствуют конечные моменты), можно вывести без необходимости специальных модификаций, таких как пропускная способность на основе IQR . Это связано с тем, что первый момент статистики порядка всегда существует, если существует ожидаемое значение базового распределения, но обратное не обязательно верно.

Работа с дискретными переменными

Предполагать $X_{1},X_{2},\ldots ,X_{n}$ являются iid случайными величинами из дискретного распределения с кумулятивной функцией распределения $F(x)$ и функция массы вероятности $f(x)$. Чтобы найти вероятности $k^{\text{th}}$ статистика порядка, сначала нужны три значения, а именно

$p_{1}=P(X<x)=F(x)-f(x),\ p_{2}=P(X=x)=f(x),{\text{ and }}p_{3}=P(X>x)=1-F(x).$

Кумулятивная функция распределения $k^{\text{th}}$ Статистику порядка можно вычислить, отметив, что

${\begin{aligned}P(X_{(k)}\leq x)&=P({\text{there are at least }}k{\text{ observations less than or equal to }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}p_{3}^{j}(p_{1}+p_{2})^{n-j}.\end{aligned}}$

Сходным образом, $P(X_{(k)}<x)$ дается

${\begin{aligned}P(X_{(k)}<x)&=P({\text{there are at least }}k{\text{ observations less than }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than or equal to }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}(p_{2}+p_{3})^{j}(p_{1})^{n-j}.\end{aligned}}$

Обратите внимание, что функция массы вероятности $X_{(k)}$ это просто разница этих значений, то есть

${\begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}\leq x)-P(X_{(k)}<x),\\&=\sum _{j=0}^{n-k}{n \choose j}\left(p_{3}^{j}(p_{1}+p_{2})^{n-j}-(p_{2}+p_{3})^{j}(p_{1})^{n-j}\right),\\&=\sum _{j=0}^{n-k}{n \choose j}\left((1-F(x))^{j}(F(x))^{n-j}-(1-F(x)+f(x))^{j}(F(x)-f(x))^{n-j}\right).\end{aligned}}$

Вычисление статистики заказов

Основные статьи: Алгоритм отбора и выборка по порядку

Задача вычисления k -го наименьшего (или наибольшего) элемента списка называется проблемой выбора и решается с помощью алгоритма выбора. Хотя эта проблема сложна для очень больших списков, были созданы сложные алгоритмы выбора, которые могут решить эту проблему за время, пропорциональное количеству элементов в списке, даже если список совершенно неупорядочен. Если данные хранятся в определенных специализированных структурах данных, это время можно сократить до O(log n ). Во многих приложениях требуется вся статистика по порядку, и в этом случае можно использовать алгоритм сортировки , а затрачиваемое на это время составляет O( n log n ).

См. также

• Ранкит
• Коробочный сюжет
• BRS-неравенство
• Сопутствующее (статистика)
• Распределение Фишера – Типпета
• Теорема Бапата–Бега о порядковой статистике независимых, но не обязательно одинаково распределенных случайных величин.
• Полином Бернштейна
• L-оценщик - линейные комбинации статистики заказов
• Распределение по рангам
• Алгоритм выбора

Примеры статистики заказов

• Примерный максимум и минимум
• Квантиль
• процентиль
• Дециль
• Квартиль
• медиана
• Иметь в виду
• Выборочное среднее и ковариация

Внешние ссылки

• Заказать статистику на PlanetMath . Проверено 2 февраля 2005 г.
• Вайсштейн, Эрик В. «Статистика заказов» . Математический мир . Проверено 2 февраля 2005 г.
• исходного кода C++ Статистика динамического порядка