Бета-дистрибутив
Функция плотности вероятности  | |||
Кумулятивная функция распределения  | |||
| Обозначения | Бета( а , б ) | ||
|---|---|---|---|
| Параметры | α > 0 форма ( реальная ) β > 0 форма ( реальная ) | ||
| Поддерживать | или | ||
где и это гамма-функция . | |||
| CDF | ( регуляризованная неполная бета-функция ) | ||
| Иметь в виду |
| ||
| медиана | |||
| Режим | для α , β > 1 любое значение в для α , β = 1 {0, 1} (бимодальный) для α , β < 1 0 для α ≤ 1, β ≥ 1, α ≠ β 1 для α ≥ 1, β ≤ 1, α ≠ β | ||
| Дисперсия | (см. тригамма-функцию и см. раздел: Геометрическая дисперсия ) | ||
| асимметрия | |||
| Избыточный эксцесс | |||
| Энтропия | |||
| МГФ | |||
| CF | (см. Вырожденная гипергеометрическая функция ) | ||
| Информация о Фишере | см. раздел: Информационная матрица Фишера. | ||
| Метод моментов | |||
В теории вероятностей и статистике бета -распределение представляет собой семейство непрерывных распределений вероятностей , определенных на интервале [0, 1] или (0, 1) с точки зрения двух положительных параметров , обозначаемых альфа ( α ) и бета ( β ), которые появляются как показатели переменной и ее дополнения к 1 соответственно и контролируют форму распределения.
Бета-распределение применялось для моделирования поведения случайных величин, ограниченных интервалами конечной длины, в самых разных дисциплинах. Бета-распределение является подходящей моделью случайного поведения процентов и пропорций.
В байесовском выводе бета-распределение представляет собой сопряженное априорное распределение вероятностей для распределений Бернулли , биномиального , отрицательного биномиального и геометрического распределений.
Формулировка обсуждаемого здесь бета-распределения также известна как бета-распределение первого рода , тогда как бета-распределение второго рода является альтернативным названием простого бета-распределения . Обобщение на несколько переменных называется распределением Дирихле .
Определения [ править ]
плотности вероятности Функция

Функция плотности вероятности (PDF) бета-распределения для или и параметры формы , , является степенной функцией переменной и его отражение следующее:
где это гамма-функция . функция Бета- , , — константа нормализации , гарантирующая, что общая вероятность равна 1. В приведенных выше уравнениях это реализация (наблюдаемое значение, которое действительно произошло) случайной величины .
Некоторые авторы, в том числе Н. Л. Джонсон и С. Коц , [1] используйте символы и (вместо и ) для параметров формы бета-распределения, напоминающих символы, традиционно используемые для параметров распределения Бернулли , поскольку бета-распределение приближается к распределению Бернулли в пределе, когда оба параметра формы и приближаться к значению нуля.
Далее случайная величина бета-распределение с параметрами и будет обозначаться: [2] [3]
Другие обозначения случайных величин с бета-распределением, используемые в статистической литературе: [4] и . [5]
распределения Кумулятивная функция

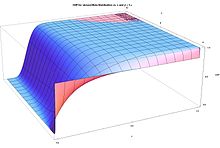
Кумулятивная функция распределения равна
где – неполная бета-функция и – регуляризованная неполная бета-функция .
Альтернативные параметризации [ править ]
Два параметра [ править ]
и размер выборки Средний размер
Бета-распределение также можно перепараметризовать с точки зрения его среднего значения µ (0 < µ < 1) и суммы двух параметров формы ν = α + β > 0 ( [3] п. 83). Обозначая через αPosterior и βPosterior параметры формы апостериорного бета-распределения, полученные в результате применения теоремы Байеса к биномиальной функции правдоподобия и априорной вероятности, интерпретация сложения обоих параметров формы как размера выборки = ν = α ·Posterior + β · Апостериорный метод верен только для априорной вероятности Холдейна Beta(0,0). В частности, для байесовской (равномерной) априорной бета-версии (1,1) правильной интерпретацией будет размер выборки = α · Posterior + β Posterior - 2 или ν = (размер выборки) + 2. Для размера выборки, намного превышающего 2, разница между этими двумя априорами становится незначительной. (Подробнее см. в разделе «Байесовский вывод ».) ν = α + β называется «размером выборки» бета-распределения, но следует помнить, что, строго говоря, это «размер выборки» биномиальной функции правдоподобия. только при использовании априорной бета-версии Холдейна (0,0) в теореме Байеса.
Эта параметризация может быть полезна при оценке байесовских параметров. Например, можно провести тест нескольким людям. Если предположить, что балл каждого человека (0 ≤ θ ≤ 1) получен из бета-распределения на уровне населения, то важной статистикой является среднее значение этого распределения на уровне населения. Параметры среднего размера и размера выборки связаны с параметрами формы α и β через [3]
- α знак равно µν , β знак равно (1 - µ ) ν
При этой параметризации можно поместить неинформативную априорную вероятность поверх среднего значения и расплывчатую априорную вероятность (например, экспоненциальное или гамма-распределение ) над положительными действительными числами для размера выборки, если они независимы, а априорные данные и/или убеждения оправдайте это.
и Режим концентрация
Вогнутые бета-распределения, которые имеют , может быть параметризован с точки зрения режима и «концентрации». Режим, и концентрация, , можно использовать для определения обычных параметров формы следующим образом: [6]
Для режима , чтобы быть четко определенным, нам нужно или эквивалентно . Если вместо этого мы определим концентрацию как , условие упрощается до и бета-плотность при и можно записать как:
где напрямую масштабирует достаточную статистику , и . Отметим также, что в пределе , распределение становится плоским.
Среднее значение и дисперсия [ править ]
Решая систему (связанных) уравнений, приведенную в предыдущих разделах как уравнения для среднего и дисперсии бета-распределения через исходные параметры α и β , можно выразить параметры α и β через среднее значение ( μ ) и дисперсия (var):
Такая параметризация бета-распределения может привести к более интуитивному пониманию, чем то, которое основано на исходных параметрах α и β . Например, выражая моду, асимметрию, избыточный эксцесс и дифференциальную энтропию через среднее значение и дисперсию:
Четыре параметра [ править ]
Бета-распределение с двумя параметрами формы α и β поддерживается в диапазоне [0,1] или (0,1). Можно изменить местоположение и масштаб распределения, введя два дополнительных параметра, представляющих минимальное a и максимальное c ( c > a ) значения распределения, [1] линейным преобразованием, заменяющим безразмерную переменную x на новую переменную y (с поддержкой [ a , c ] или ( a , c )) и параметры a и c :
Функция плотности вероятности бета-распределения с четырьмя параметрами равна распределению с двумя параметрами, масштабированному по диапазону ( c − a ) (так что общая площадь под кривой плотности равна вероятности единицы) и с «y " переменная сдвинута и масштабирована следующим образом:
То, что случайная величина Y имеет бета-распределение с четырьмя параметрами α, β, a и c, будет обозначаться:
Некоторые меры центрального расположения масштабируются (на ( c − a )) и сдвигаются (на a ) следующим образом:
Примечание. Среднее геометрическое и среднее гармоническое не могут быть преобразованы с помощью линейного преобразования так, как это могут сделать среднее, медиана и мода.
Параметры формы Y можно записать через его среднее значение и дисперсию как
Меры статистической дисперсии масштабируются (их не нужно сдвигать, поскольку они уже центрированы по среднему значению) по диапазону ( c − a ), линейно для среднего отклонения и нелинейно для дисперсии:
Поскольку асимметрия и избыточный эксцесс являются безразмерными величинами (как моменты, центрированные по среднему значению и нормированные стандартным отклонением ), они не зависят от параметров a и c и, следовательно, равны выражениям, приведенным выше через X (с поддержка [0,1] или (0,1)):
Свойства [ править ]
центральной тенденции Меры
Режим [ править ]
Мода случайной бета-распределенной величины X с α , β > 1 является наиболее вероятным значением распределения (соответствующим пику в PDF) и определяется следующим выражением: [1]
Когда оба параметра меньше единицы ( α , β <1), это антирежим: самая нижняя точка кривой плотности вероятности. [7]
Полагая α = β , выражение для моды упрощается до 1/2, показывая, что при α = β > 1 мода (соответственно антимода, когда α , β < 1 ) находится в центре распределения: это симметричны в этих случаях. См. раздел «Фигуры» в этой статье для получения полного списка режимов для произвольных значений α и β . В некоторых из этих случаев максимальное значение функции плотности приходится на один или оба конца. В некоторых случаях (максимальное) значение функции плотности, встречающееся в конце, конечно. Например, в случае α = 2, β = 1 (или α = 1, β = 2) функция плотности становится распределением прямоугольного треугольника , которое является конечным на обоих концах. В ряде других случаев на одном конце имеется особенность , где значение функции плотности приближается к бесконечности. Например, в случае α = β = 1/2 бета-распределение упрощается и становится арксинусным распределением . Среди математиков ведутся споры о некоторых из этих случаев и о том, концы ( x = 0 и x можно ли называть = 1) модами или нет. [8] [2]

- Являются ли концы частью области определения функции плотности
- Можно ли когда-нибудь сингулярность назвать модой
- Следует ли называть случаи с двумя максимумами бимодальными
Медиана [ править ]
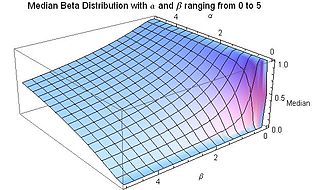

Медиана бета-распределения — это уникальное действительное число. для которой регуляризованная неполная бета-функция . Не существует общего выражения в замкнутой форме для медианы бета-распределения для произвольных значений α и β . Ниже приведены выражения в замкнутой форме для конкретных значений параметров α и β : [ нужна ссылка ]
- Для симметричных случаев α = β медиана = 1/2.
- Для α = 1 и β > 0 медиана (этот случай является зеркальным отражением распределения степенной функции [0,1])
- Для α > 0 и β = 1 медиана = (этот случай представляет собой распределение степенной функции [0,1] [8] )
- Для α = 3 и β = 2 медиана = 0,6142724318676105..., вещественное решение уравнения четвертой степени 1 − 8 x 3 + 6x 4 = 0, лежащий в [0,1].
- Для α = 2 и β = 3 медиана = 0,38572756813238945... = 1 − медиана(бета(3, 2))
Ниже приведены пределы, в которых один параметр конечен (ненулевой), а другой приближается к этим пределам: [ нужна ссылка ]
Разумное приближение значения медианы бета-распределения, как для α, так и для β, большего или равного единице, дается формулой [9]
При α, β ≥ 1 относительная ошибка ( абсолютная ошибка, деленная на медиану) в этом приближении составляет менее 4%, а как при α ≥ 2, так и при β ≥ 2 – менее 1%. Абсолютная ошибка, деленная на разницу между средним значением и модой, также мала:
Среднее [ править ]

Ожидаемое значение (среднее значение) ( μ бета-распределения ) случайной величины X с двумя параметрами α и β является функцией только отношения β / α этих параметров: [1]
Полагая α = β в приведенном выше выражении, получаем µ = 1/2 , показывая, что для α = β среднее значение находится в центре распределения: оно симметрично. Кроме того, из приведенного выше выражения можно получить следующие пределы:
Следовательно, для β / α → 0 или для α / β → ∞ среднее значение расположено на правом конце, x = 1 . Для этих предельных отношений бета-распределение становится одноточечным вырожденным распределением с пиком дельта-функции Дирака на правом конце, x = 1 , с вероятностью 1 и нулевой вероятностью везде. Существует 100% вероятность (абсолютная уверенность), сосредоточенная на правом конце, x = 1 .
Аналогично, для β / α → ∞ или для α / β → 0 среднее значение расположено на левом конце, x = 0 . Бета-распределение становится 1-точечным вырожденным распределением с пиком дельта-функции Дирака на левом конце, x = 0, с вероятностью 1 и нулевой вероятностью везде. Существует 100% вероятность (абсолютная уверенность), сконцентрированная на левом конце, x = 0. Ниже приведены пределы, в которых один параметр конечен (отличен от нуля), а другой приближается к этим пределам:
В то время как для типичных унимодальных распределений (с центрально расположенными модами, точками перегиба по обе стороны от моды и более длинными хвостами) (с Beta( α , β ) такими, что α , β > 2 ) известно, что выборочное среднее (как оценка местоположения) не так устойчива , как выборочная медиана, противоположное имеет место для однородных или «U-образных» бимодальных распределений (с Beta( α , β ) такими, что α , β ≤ 1 ), с модами, расположенными в концы распределения. Как отмечают Мостеллер и Тьюки ( [10] п. 207) «среднее значение двух крайних наблюдений использует всю выборочную информацию. Это показывает, как для распределений с коротким хвостом крайние наблюдения должны получить больший вес». Напротив, из этого следует, что медиана «U-образных» бимодальных распределений с модами на краю распределения (с Beta( α , β ) такой, что α , β ≤ 1 ) не является устойчивой, поскольку выборочная медиана снижает крайние выборочные наблюдения из рассмотрения. Практическое применение этого происходит, например, для случайных блужданий , поскольку вероятность времени последнего посещения начала координат в случайном блуждании распределяется как арксинусное распределение Beta(1/2, 1/2): [5] [11] среднее значение ряда реализаций случайного блуждания является гораздо более надежной оценкой, чем медиана (которая в данном случае является неподходящей оценкой выборочной меры).
Среднее геометрическое [ править ]



Логарифм среднего геометрического G X распределения со случайной величиной X является средним арифметическим ln( X ) или, что то же самое, его ожидаемым значением:
Для бета-распределения интеграл ожидаемого значения дает:
где ψ – дигамма-функция .
Следовательно, среднее геометрическое бета-распределения с параметрами формы α и β является экспонентой дигамм-функций α и β следующим образом:
В то время как для бета-распределения с равными параметрами формы α = β следует, что асимметрия = 0 и мода = среднее = медиана = 1/2, среднее геометрическое меньше 1/2: 0 < G X < 1/2 . Причина этого в том, что логарифмическое преобразование сильно взвешивает значения X , близкие к нулю, поскольку ln( X ) сильно стремится к отрицательной бесконечности, когда X приближается к нулю, тогда как ln( X ) выравнивается к нулю при X → 1 .
Вдоль прямой α = β применяются следующие ограничения:
Ниже приведены пределы, в которых один параметр конечен (отличен от нуля), а другой приближается к этим пределам:
Прилагаемый график показывает разницу между средним и средним геометрическим для параметров формы α и β от нуля до 2. Помимо того факта, что разница между ними приближается к нулю, когда α и β приближаются к бесконечности, и что разница становится большой для значений α и β, приближающихся к нулю, можно наблюдать очевидную асимметрию среднего геометрического относительно параметров формы α и β. Разница между средним геометрическим и средним больше для малых значений α по отношению к β, чем при обмене величинами β и α.
Н.Л.Джонсон и С.Коц [1] предложить логарифмическую аппроксимацию дигамма-функции ψ ( α ) ≈ ln( α − 1/2), что приводит к следующему приближению к среднему геометрическому:
Численные значения относительной ошибки в этом приближении следующие: [ ( α = β = 1): 9,39% ]; [ ( α = β = 2): 1,29% ]; [ ( а =2, b =3): 1,51% ]; [ ( α = 3, β = 2): 0,44% ]; [ ( α = β = 3): 0,51% ]; [ ( α = β = 4): 0,26% ]; [ ( а =3, b =4): 0,55% ]; [ ( α = 4, β = 3): 0,24% ].
Аналогично можно вычислить значение параметров формы, необходимое для того, чтобы среднее геометрическое было равно 1/2. Учитывая значение параметра β , каким будет значение другого параметра α , необходимого для того, чтобы среднее геометрическое равнялось 1/2? Ответ заключается в том, что (при β > 1 ) требуемое значение α стремится к β + 1/2 при β → ∞ . Например, все эти пары имеют одинаковое среднее геометрическое 1/2: [ β = 1, α = 1,4427 ], [ β = 2, α = 2,46958 ], [ β = 3, α = 3,47943 ], [ β = 4 , α = 4,48449 ], [ β = 5, α = 5,48756 ], [ β = 10, α = 10,4938 ], [ β = 100, α = 100,499 ].
Фундаментальное свойство среднего геометрического, ложность которого можно доказать для любого другого среднего, состоит в том, что
Это делает среднее геометрическое единственным правильным средним значением при усреднении нормализованных результатов, то есть результатов, представленных как отношения к эталонным значениям. [12] Это актуально, поскольку бета-распределение является подходящей моделью для случайного поведения процентов и особенно подходит для статистического моделирования пропорций. Среднее геометрическое играет центральную роль в оценке максимального правдоподобия, см. раздел «Оценка параметров, максимальное правдоподобие». Действительно, при выполнении оценки максимального правдоподобия, помимо среднего геометрического G X, основанного на случайной величине X, естественным образом появляется и другое среднее геометрическое: среднее геометрическое, основанное на линейном преобразовании – (1 − X ) , зеркальное отображение X , обозначается G (1− X ) :
Вдоль прямой α = β применяются следующие ограничения:
Ниже приведены пределы, в которых один параметр конечен (отличен от нуля), а другой приближается к этим пределам:
Он имеет следующую приблизительную стоимость:
Хотя и G X , и G (1- X ) асимметричны, в случае, когда оба параметра формы равны α = β , средние геометрические равны: G X = G (1- X ) . Это равенство следует из следующей симметрии, проявляемой между обоими средними геометрическими:
Гармоническое среднее [ править ]




Обратное к среднему гармоническому ( H X ) распределения со случайной величиной X является средним арифметическим 1/ X или, что то же самое, его ожидаемым значением. Следовательно, среднее гармоническое ( H X ) бета-распределения с параметрами формы α и β равно:
Среднее гармоническое ( H X ) бета-распределения с α <1 не определено, поскольку его определяющее выражение не ограничено в [0, 1] для параметра формы α меньше единицы.
Полагая α = β в приведенном выше выражении, получаем
показывая, что для α = β среднее гармоническое колеблется от 0, для α = β = 1, до 1/2, для α = β → ∞.
Ниже приведены пределы, в которых один параметр конечен (отличен от нуля), а другой приближается к этим пределам:
Среднее гармоническое играет роль в оценке максимального правдоподобия для случая четырех параметров в дополнение к среднему геометрическому. Фактически, при выполнении оценки максимального правдоподобия для случая четырех параметров, помимо гармонического среднего H X на основе случайной величины X , естественным образом появляется еще одно гармоническое среднее: гармоническое среднее, основанное на линейном преобразовании (1 − X ), зеркальное образ X , обозначаемый H 1 − X :
Среднее гармоническое ( H (1 − X ) ) бета-распределения с β <1 не определено, поскольку его определяющее выражение не ограничено в [0, 1] для параметра формы β меньше единицы.
Полагая α = β в приведенном выше выражении, получаем
показывая, что для α = β среднее гармоническое колеблется от 0, для α = β = 1, до 1/2, для α = β → ∞.
Ниже приведены пределы, в которых один параметр конечен (отличен от нуля), а другой приближается к этим пределам:
Хотя и H X , и H 1− X асимметричны, в случае, когда оба параметра формы равны α = β , гармонические средние равны: H X = H 1− X . Это равенство следует из следующей симметрии, проявляемой между обоими гармоническими средними:
Меры статистической дисперсии
Дисперсия [ править ]
Дисперсия бета-распределения с (второй момент, центрированный по среднему значению) случайной величины X параметрами α и β равна: [1] [13]
Полагая α = β в приведенном выше выражении, получаем
показывая, что при α = β дисперсия монотонно уменьшается с увеличением α = β . Полагая в этом выражении α = β = 0 , можно найти максимальную дисперсию var( X ) = 1/4. [1] что происходит только при приближении к пределу, при α = β = 0 .
Бета-распределение также может быть параметризовано с точки зрения его среднего значения ц (0 < ц < 1) и размера выборки ν = α + β ( ν > 0 ) (см. подраздел «Среднее значение и размер выборки» ):
Используя эту параметризацию , можно выразить дисперсию через среднее значение μ и размер выборки ν следующим образом:
Поскольку ν = α + β > 0 , отсюда следует, что var( X ) < µ (1 − µ ) .
Для симметричного распределения среднее значение находится в середине распределения, μ = 1/2 , и, следовательно:
Кроме того, из приведенных выше выражений можно получить следующие пределы (при этом только отмеченная переменная приближается к пределу):
и ковариация Геометрическая дисперсия


Логарифм геометрической дисперсии ln(var GX ) распределения со случайной величиной X — это второй момент логарифма X, центрированный на среднем геометрическом X , ln( G X ):
и, следовательно, геометрическая дисперсия равна:
В информационной матрице Фишера и кривизне логарифмической функции правдоподобия появляются логарифм геометрической дисперсии отражаемой переменной 1 - X и логарифм геометрической ковариации между X и 1 - X :
Для бета-распределения логарифмические моменты более высокого порядка могут быть получены путем использования представления бета-распределения как доли двух гамма-распределений и дифференцирования через интеграл. Их можно выразить через полигамма-функции более высокого порядка. См. раздел § Моменты логарифмически преобразованных случайных величин . Дисперсия ) логарифмических переменных и ковариация ln X и ln(1− X :
где тригамма-функция , обозначаемая ψ 1 (α), является второй из полигамма-функций и определяется как производная дигамма-функции :
Поэтому,
Прилагаемые графики показывают логарифмические геометрические отклонения и логарифмическую геометрическую ковариацию в зависимости от параметров формы α и β . Графики показывают, что логарифмические геометрические дисперсии и логарифмическая геометрическая ковариация близки к нулю для параметров формы α и β, превышающих 2, и что значение логарифмических геометрических дисперсий быстро возрастает для значений параметров формы α и β меньше единицы. Логарифмические геометрические отклонения положительны для всех значений параметров формы. Логарифмическая геометрическая ковариация отрицательна для всех значений параметров формы и достигает больших отрицательных значений для α и β меньше единицы.
Ниже приведены пределы, в которых один параметр конечен (отличен от нуля), а другой приближается к этим пределам:
Пределы с изменением двух параметров:
Хотя и ln(var GX ), и ln(var G (1 − X ) ) асимметричны, когда параметры формы равны, α = β, имеем: ln(var GX ) = ln(var G(1−X) ). Это равенство следует из следующей симметрии, отображаемой между обоими логарифмическими геометрическими отклонениями:
Логарифмическая геометрическая ковариация симметрична:
Среднее абсолютное отклонение от среднего [ править ]


Среднее абсолютное отклонение от среднего значения для бета-распределения с параметрами формы α и β составляет: [8]
Среднее абсолютное отклонение от среднего является более надежной оценкой статистической дисперсии с хвостами и точками перегиба на каждой стороне моды, бета- α , β распределений с , чем стандартное отклонение для бета - распределений > 2, поскольку оно зависит от линейных (абсолютных) отклонений, а не от квадратных отклонений от среднего значения. Таким образом, влияние очень больших отклонений от среднего значения не так уж сильно переоценено.
Используя приближение Стирлинга к гамма-функции , Н.Л.Джонсон и С.Коц [1] вывел следующую аппроксимацию для значений параметров формы, больших единицы (относительная погрешность этого приближения составляет всего -3,5% при α = β = 1 и уменьшается до нуля при α → ∞, β → ∞):
В пределе α → ∞, β → ∞ отношение среднего абсолютного отклонения к стандартному отклонению (для бета-распределения) становится равным отношению тех же мер для нормального распределения: . При α = β = 1 это соотношение равно , так что от α = β = 1 до α, β → ∞ отношение уменьшается на 8,5%. Для α = β = 0 стандартное отклонение точно равно среднему абсолютному отклонению от среднего значения. Следовательно, это отношение уменьшается на 15% от α = β = 0 до α = β = 1 и на 25% от α = β = 0 до α, β → ∞. Однако для асимметричных бета-распределений, таких, что α → 0 или β → 0, отношение стандартного отклонения к среднему абсолютному отклонению приближается к бесконечности (хотя каждое из них по отдельности приближается к нулю), поскольку среднее абсолютное отклонение приближается к нулю быстрее, чем стандартное отклонение.
Используя параметризацию в терминах среднего значения µ и размера выборки ν = α + β > 0:
- α = µν, β = (1−µ)ν
от среднего значения можно выразить среднее абсолютное отклонение через среднее значение μ и размер выборки ν следующим образом:
Для симметричного распределения среднее значение находится в середине распределения, μ = 1/2, и, следовательно:
Кроме того, из приведенных выше выражений можно получить следующие пределы (при этом только отмеченная переменная приближается к пределу):
Средняя абсолютная разница
Средняя абсолютная разница для бета-распределения равна:
Коэффициент Джини для бета-распределения составляет половину относительной средней абсолютной разницы:
Асимметрия [ править ]

Асимметрия (третий момент , сосредоточенный на среднем значении, нормированный на степень дисперсии 3/2) бета-распределения равна [1]
Полагая α = β в приведенном выше выражении, получаем γ 1 = 0, что еще раз показывает, что при α = β распределение симметрично и, следовательно, асимметрия равна нулю. Положительный перекос (правый) для α < β, отрицательный перекос (левосторонний) для α > β.
Используя параметризацию в терминах среднего значения µ и размера выборки ν = α + β:
асимметрию можно выразить через среднее значение µ и размер выборки ν следующим образом:
Асимметрию также можно выразить через дисперсию var и среднее значение µ следующим образом:
Прилагаемый график асимметрии как функции дисперсии и среднего показывает, что максимальная дисперсия (1/4) связана с нулевой асимметрией и условием симметрии (μ = 1/2), и что максимальная асимметрия (положительная или отрицательная бесконечность) возникает, когда среднее значение расположено на одном или другом конце, так что «масса» распределения вероятностей сосредоточена на концах (минимальная дисперсия).
Следующее выражение для квадрата асимметрии через размер выборки ν = α + β и дисперсию var полезно для метода оценки моментов четырех параметров:
Это выражение правильно дает нулевую асимметрию для α = β, поскольку в этом случае (см. § Дисперсия ): .
Для симметричного случая (α = β) асимметрия = 0 во всем диапазоне и применяются следующие ограничения:
Для асимметричных случаев (α ≠ β) из приведенных выше выражений можно получить следующие пределы (при этом только отмеченная переменная приближается к пределу):
Куртосис [ править ]

Бета-распределение применялось в акустическом анализе для оценки повреждений зубчатых колес, поскольку эксцесс бета-распределения считается хорошим индикатором состояния зубчатого колеса. [14] Куртозис также использовался, чтобы отличить сейсмический сигнал, генерируемый шагами человека, от других сигналов. Поскольку люди или другие цели, движущиеся по земле, генерируют непрерывные сигналы в виде сейсмических волн, можно разделить разные цели на основе генерируемых ими сейсмических волн. Куртозис чувствителен к импульсивным сигналам, поэтому он гораздо более чувствителен к сигналу, генерируемому человеческими шагами, чем к другим сигналам, генерируемым транспортными средствами, ветром, шумом и т. д. [15] К сожалению, обозначение эксцесса не стандартизировано. Кенни и Кепинг [16] используйте символ γ 2 для обозначения избыточного эксцесса , но Абрамовиц и Стегун [17] использовать другую терминологию. Во избежание путаницы [18] между эксцессом (четвертый момент, центрированный по среднему, нормированному на квадрат дисперсии) и избыточным эксцессом при использовании символов будут записываться следующим образом: [8] [19]
Полагая α = β в приведенном выше выражении, получаем
- .
Следовательно, для симметричных бета-распределений избыточный эксцесс отрицательен, увеличиваясь от минимального значения -2 в пределе при {α = β} → 0 и приближаясь к максимальному значению, равному нулю при {α = β} → ∞. Значение -2 — это минимальное значение избыточного эксцесса, которого может когда-либо достичь любое распределение (не только бета-распределение, но и любое распределение любого возможного вида). Это минимальное значение достигается, когда вся плотность вероятности полностью сконцентрирована на каждом конце x = 0 и x = 1, и между ними нет ничего: двухточечное распределение Бернулли с равной вероятностью 1/2 на каждом конце (подбрасывание монеты: см. раздел ниже «Куртозис, ограниченный квадратом асимметрии» для дальнейшего обсуждения). Описание эксцесса как меры «потенциальных выбросов» (или «потенциально редких, экстремальных значений») распределения вероятностей верно для всех распределений, включая бета-распределение. Если в бета-распределении могут встречаться редкие экстремальные значения, тем выше его эксцесс; в противном случае эксцесс будет ниже. Для α ≠ β, асимметричного бета-распределения, избыточный эксцесс может достигать неограниченных положительных значений (особенно для α → 0 для конечного β или для β → 0 для конечного α), поскольку сторона, находящаяся от моды, будет время от времени давать экстремальные значения. Минимальный эксцесс имеет место, когда плотность массы одинаково сконцентрирована на каждом конце (и, следовательно, среднее значение находится в центре), и между концами нет вероятностной плотности массы.
Используя параметризацию в терминах среднего значения µ и размера выборки ν = α + β:
можно выразить избыточный эксцесс через среднее значение μ и размер выборки ν следующим образом:
Избыточный эксцесс также может быть выражен через следующие два параметра: дисперсию var и размер выборки ν следующим образом:
и с точки зрения дисперсии var и среднего µ следующим образом:
График избыточного эксцесса как функции дисперсии и среднего значения показывает, что минимальное значение избыточного эксцесса (-2, которое является минимально возможным значением избыточного эксцесса для любого распределения) тесно связано с максимальным значением дисперсии ( 1/4) и условие симметрии: среднее значение, происходящее в средней точке (μ = 1/2). Это происходит для симметричного случая α = β = 0 с нулевой асимметрией. В пределе это двухточечное распределение Бернулли с равной вероятностью 1/2 на каждом дельта-функции Дирака конце x = 0 и x = 1 и нулевой вероятностью везде. (Подбрасывание монеты: одна грань монеты равна x = 0, а другая сторона равна x = 1.) Дисперсия максимальна, потому что распределение является бимодальным, и между двумя модами (пиками) на каждом конце нет ничего промежуточного. Избыточный эксцесс минимален: плотность вероятности «масса» равна нулю в среднем и сосредоточена на двух пиках на каждом конце. Избыточный эксцесс достигает минимально возможного значения (для любого распределения), когда функция плотности вероятности имеет два пика на каждом конце: она является би- «пиковой», и между ними нет ничего.
С другой стороны, график показывает, что для случаев крайнего перекоса, когда среднее значение расположено вблизи одного или другого конца (μ = 0 или μ = 1), дисперсия близка к нулю, а избыточный эксцесс быстро приближается к бесконечности, когда среднее значение распределения приближается к любому концу.
Альтернативно, избыточный эксцесс также может быть выражен через следующие два параметра: квадрат асимметрии и размер выборки ν следующим образом:
Из этого последнего выражения можно получить те же пределы, опубликованные более века назад Карлом Пирсоном. [20] для бета-распределения (см. раздел ниже под названием «Куртозис, ограниченный квадратом асимметрии»). Полагая α + β = ν = 0 в приведенном выше выражении, получаем нижнюю границу Пирсона (значения асимметрии и избыточного эксцесса ниже границы (избыточный эксцесс + 2 − асимметрия 2 = 0) не может произойти ни при каком распределении, и поэтому Карл Пирсон правильно назвал область ниже этой границы «невозможной областью»). Предел α + β = ν → ∞ определяет верхнюю границу Пирсона.
поэтому:
Значения ν = α + β, такие, что ν находится в диапазоне от нуля до бесконечности, 0 < ν < ∞, охватывают всю область бета-распределения в плоскости избыточного эксцесса по сравнению с квадратом асимметрии.
Для симметричного случая ( α = β ) применяются следующие ограничения:
Для несимметричных случаев ( α ≠ β ) из приведенных выше выражений можно получить следующие пределы (при этом только отмеченная переменная приближается к пределу):
Характеристическая функция [ править ]
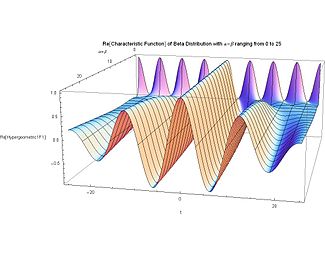




Характеристическая функция представляет собой преобразование Фурье функции плотности вероятности. Характеристической функцией бета-распределения является вырожденная гипергеометрическая функция Куммера (первого рода): [1] [17] [21]
где
— это восходящий факториал , также называемый «символом Поххаммера». Значение характеристической функции при t = 0 равно единице:
Кроме того, действительная и мнимая части характеристической функции обладают следующими симметриями относительно начала координат переменной t :
Симметричный случай α = β упрощает характеристическую функцию бета-распределения до функции Бесселя , поскольку в частном случае α + β = 2α вырожденная гипергеометрическая функция (первого рода) сводится к функции Бесселя (модифицированной функции Бесселя первый вид ), используя второе преобразование Куммера следующим образом:
На прилагаемых графиках действительная часть (Re) характеристической функции бета-распределения отображается для симметричного (α = β) и асимметричного (α ≠ β) случаев.
Другие моменты [ править ]
Функция генерации момента [ править ]
Из этого также следует [1] [8] что производящая функция момента равна
В частности, M X ( α ; β ; 0) = 1.
Высшие моменты [ править ]
Используя функцию, производящую момент , k -й необработанный момент определяется выражением [1] фактор
умножение члена (экспоненциального ряда) в ряду производящей функции момента
где ( х ) ( к ) — это символ Поххаммера, обозначающий возрастающий факториал. Его также можно записать в рекурсивной форме как
Поскольку в момент производящая функция имеет положительный радиус сходимости, бета-распределение определяется его моментами . [22]
Моменты преобразованных случайных величин [ править ]
Моменты линейно преобразованных, продуктовых и случайных инвертированных величин
Можно также показать следующие ожидания для преобразованной случайной величины: [1] где случайная величина X имеет бета-распределение с параметрами α и β : X ~ Beta( α , β ). Ожидаемое значение переменной 1 - X представляет собой зеркальную симметрию ожидаемого значения, основанного на X :
Из-за зеркальной симметрии функции плотности вероятности бета-распределения дисперсии, основанные на переменных X и 1 - X , идентичны, а ковариация по X (1 - X является отрицательной дисперсией:
Это ожидаемые значения для инвертированных переменных (они связаны со средними гармониками, см. § Среднее гармоническое ):
Следующее преобразование путем деления переменной X на ее зеркальное отображение X /(1 − X ) приводит к ожидаемому значению «перевернутого бета-распределения» или простого бета-распределения (также известного как бета-распределение второго рода или типа VI Пирсона) . ): [1]
Дисперсии этих преобразованных переменных можно получить путем интегрирования, как ожидаемые значения вторых моментов, сосредоточенных на соответствующих переменных:
Следующая дисперсия переменной X, деленная на ее зеркальное отображение ( X /(1− X ), приводит к дисперсии «перевернутого бета-распределения» или простого бета-распределения (также известного как бета-распределение второго рода или типа VI Пирсона). ): [1]
Ковариации:
Эти ожидания и отклонения появляются в четырехпараметрической информационной матрице Фишера ( § Информация Фишера .)
Моменты логарифмически преобразованных случайных величин
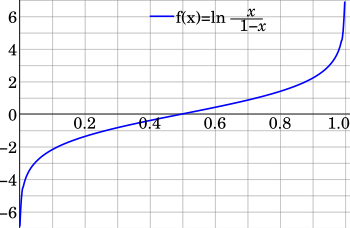
ожидаемые значения для логарифмических преобразований (полезно для оценок максимального правдоподобия , см. § Оценка параметров, Максимальное правдоподобие В этом разделе обсуждаются ). Следующие логарифмические линейные преобразования связаны со средними геометрическими G X и G (1− X ) (см. § Среднее геометрическое ):
Где дигамма-функция ψ(α) определяется как логарифмическая производная гамма -функции : [17]
Логит- преобразования интересны. [23] поскольку они обычно преобразуют различные формы (включая J-образные формы) в (обычно перекошенные) колоколообразные плотности по логит-переменной и могут удалять конечные особенности по исходной переменной:
Джонсон [24] рассмотрено распределение логит - преобразованной переменной ln( X /1 − X ), включая ее производящую функцию момента и аппроксимации для больших значений параметров формы. Это преобразование расширяет конечный носитель [0, 1] на основе исходной переменной X до бесконечного носителя в обоих направлениях вещественной линии (−∞, +∞). Логит бета-переменной имеет логистическое бета-распределение .
Логарифмические моменты более высокого порядка можно получить, используя представление бета-распределения как пропорции двух гамма-распределений и дифференцируя его через интеграл. Их можно выразить через полигамма-функции более высокого порядка следующим образом:
следовательно, дисперсия логарифмических переменных и ковариация ln( X ) и ln(1− X ) равны:
где тригамма-функция , обозначаемая ψ 1 ( α ), является второй из полигамма-функций и определяется как производная дигамма- функции:
Дисперсии и ковариации логарифмически преобразованных переменных X и (1 − X ), как правило, различны, потому что логарифмическое преобразование разрушает зеркальную симметрию исходных переменных X и (1 − X ), поскольку логарифм приближается к отрицательной бесконечности для переменная приближается к нулю.
Эти логарифмические отклонения и ковариация являются элементами информационной матрицы Фишера для бета-распределения. Они также являются мерой кривизны логарифмической функции правдоподобия (см. раздел «Оценка максимального правдоподобия»).
Дисперсии логарифмических обратных переменных идентичны дисперсиям логарифмических переменных:
Отсюда также следует, что дисперсии логит -преобразованных переменных равны
Количества информации (энтропия) [ править ]
Учитывая бета-распределенную случайную величину, ~ Beta( α , β ), дифференциальная энтропия X X равна (измеряется в натс ), [25] ожидаемое значение отрицательного логарифма функции плотности вероятности :
где f ( x ; α , β ) — функция плотности вероятности бета-распределения:
Дигамма -функция ψ появляется в формуле дифференциальной энтропии как следствие интегральной формулы Эйлера для чисел гармоник , которая следует из интеграла:
Дифференциальная энтропия бета-распределения отрицательна для всех значений α и β, больших нуля, за исключением α = β = 1 (для которых значения бета-распределения такие же, как и равномерное распределение ), где дифференциальная энтропия достигает своего максимума. значение ноль. Следует ожидать, что максимум энтропии должен иметь место тогда, когда бета-распределение становится равным равномерному распределению, поскольку неопределенность максимальна, когда все возможные события равновероятны.
Если α или β приближаются к нулю, дифференциальная энтропия приближается к минимальному значению отрицательной бесконечности. Для (или обоих) α или β , приближающихся к нулю, существует максимальная степень порядка: вся плотность вероятности сосредоточена на концах, а в точках, расположенных между концами, плотность вероятности равна нулю. Точно так же для (или обоих) α или β, стремящихся к бесконечности, дифференциальная энтропия приближается к своему минимальному значению отрицательной бесконечности и максимальной степени порядка. Если один из α или β приближается к бесконечности (а другой конечен), вся плотность вероятности сосредоточена на конце, а плотность вероятности везде равна нулю. Если оба параметра формы равны (симметричный случай), α = β , и они одновременно приближаются к бесконечности, плотность вероятности становится пиком ( дельта-функция Дирака ), сосредоточенным в середине x = 1/2, и, следовательно, существует 100% вероятность в середине x = 1/2 и нулевая вероятность везде.
(непрерывный случай) Дифференциальная энтропия была введена Шенноном в его оригинальной статье (где он назвал ее «энтропией непрерывного распределения») как заключительная часть той же статьи, где он определил дискретную энтропию . [26] С тех пор известно, что дифференциальная энтропия может отличаться от бесконечно малого предела дискретной энтропии на бесконечное смещение, поэтому дифференциальная энтропия может быть отрицательной (как и для бета-распределения). Что действительно имеет значение, так это относительная величина энтропии.
Учитывая две бета-распределенные случайные величины, X 1 ~ Beta( α , β ) и X 2 ~ Beta( α ′ , β ′ ), перекрестная энтропия (измеряется в натуральных числах) [27]
Перекрестная энтропия использовалась в качестве показателя ошибки для измерения расстояния между двумя гипотезами. [28] [29] Его абсолютное значение минимально, когда два распределения идентичны. Это информационная мера, наиболее тесно связанная с журналом максимального правдоподобия. [27] (см. раздел «Оценка параметров. Оценка максимального правдоподобия»)).
Относительная энтропия, или дивергенция Кульбака–Лейблера D KL ( X 1 || X 2 ), является мерой неэффективности предположения, что распределение X 2 ~ Beta ( α ′ , β ′ ), когда распределение действительно X 1 ~ Бета( α , β ). Он определяется следующим образом (измеряется в натс).
Относительная энтропия, или дивергенция Кульбака-Лейблера , всегда неотрицательна. Ниже приведены несколько числовых примеров:
- Х 1 ~ Бета(1, 1) и Х 2 ~ Бета(3, 3); Д КЛ ( Икс 1 || Х 2 ) = 0,598803; D КЛ ( Икс 2 || Икс 1 ) = 0,267864; час ( Икс 1 ) = 0; час ( Икс 2 ) знак равно -0,267864
- Х 1 ~ Бета(3, 0,5) и Х 2 ~ Бета(0,5, 3); Д КЛ ( Икс 1 || Икс 2 ) = 7,21574; D кл ( Икс 2 || Икс 1 ) = 7,21574; час ( Икс 1 ) = -1,10805; час ( Икс 2 ) = -1,10805.
Дивергенция Кульбака –Лейблера не является симметричной D KL ( X 1 || X 2 ) ≠ D KL ( X 2 || X 1 ) для случая, когда отдельные бета-распределения Beta(1, 1) и Beta(3, 3) ) симметричны, но имеют разную энтропию h ( X 1 ) ≠ h ( X 2 ). Значение дивергенции Кульбака зависит от направления движения: от более высокой (дифференциальной) энтропии к более низкой (дифференциальной) энтропии или наоборот. В приведенном выше числовом примере расхождение Кульбака измеряет неэффективность предположения о том, что распределение имеет форму (колокола) Beta(3, 3), а не (равномерного) Beta(1, 1). Энтропия «h» бета (1, 1) выше, чем энтропия «h» бета (3, 3), потому что равномерное распределение бета (1, 1) имеет максимальную степень беспорядка. Дивергенция Кульбака более чем в два раза выше (0,598803 вместо 0,267864) при измерении в направлении уменьшения энтропии: направлении, которое предполагает, что (равномерное) распределение Бета(1, 1) является (колокольчатым) Бета(3, 3), а не наоборот. В этом узком смысле расхождение Кульбака согласуется с второй закон термодинамики .
Дивергенция Кульбака –Лейблера симметрична D KL ( X 1 || X 2 ) = D KL ( X 2 || X 1 ) для асимметричных случаев Beta(3, 0,5) и Beta(0,5, 3), которые имеют одинаковую дифференциальную энтропию. час ( Икс 1 ) знак равно час ( Икс 2 ).
Условие симметрии:
следует из приведенных выше определений и зеркальной симметрии f ( x ; α , β ) = f (1 − x ; α , β ), которой обладает бета-распределение.
между статистическими показателями Отношения
, мода и медианная Среднее значение связь
Если 1 < α < β, то мода ≤ медиана ≤ среднее значение. [9] Выражая моду (только для α, β > 1) и среднее значение через α и β:
Если 1 < β < α, то порядок неравенств меняется на обратный. Для α, β > 1 абсолютное расстояние между средним значением и медианой составляет менее 5% расстояния между максимальным и минимальным значениями x . С другой стороны, абсолютное расстояние между средним значением и модой может достигать 50% расстояния между максимальным и минимальным значениями x для ( патологического ) случая α = 1 и β = 1, для которых значения бета распределение приближается к равномерному распределению, а дифференциальная энтропия приближается к своему максимальному значению и, следовательно, к максимальному «беспорядку».
Например, для α = 1,0001 и β = 1,00000001:
- режим = 0,9999; PDF(режим) = 1,00010
- среднее = 0,500025; PDF(среднее) = 1,00003
- медиана = 0,500035; PDF(медиана) = 1,00003
- среднее значение — режим = —0,499875
- среднее значение — медиана = —9,65538 × 10 −6
где PDF означает значение функции плотности вероятности .
Отношения среднего, среднего геометрического и среднего гармонического [ править ]

известно Из неравенства средних арифметических и геометрических , что среднее геометрическое ниже среднего. Точно так же среднее гармоническое ниже среднего геометрического. Прилагаемый график показывает, что для α = β и среднее, и медиана точно равны 1/2, независимо от значения α = β, а мода также равна 1/2 для α = β > 1, однако средние геометрические и гармонические значения ниже 1/2 и приближаются к этому значению только асимптотически при α = β → ∞.
асимметрии ограниченный квадратом , Эксцесс

Как заметил Феллер , [5] в системе Пирсона плотность вероятности бета отображается как тип I (любая разница между бета-распределением и распределением Пирсона типа I является лишь поверхностной и не имеет значения для последующего обсуждения взаимосвязи между эксцессом и асимметрией). Карл Пирсон показал на Таблице 1 своей статьи [20] опубликовал в 1916 году график с эксцессом в качестве вертикальной оси ( ордината ) и квадратом асимметрии в качестве горизонтальной оси ( абсцисса ), на котором был отображен ряд распределений. [30] Область, занимаемая бета-распределением, ограничена следующими двумя линиями в (асимметрии 2 ,эксцесс) плоскость или (асимметрия 2 ,избыточный эксцесс) плоскости :
или, что то же самое,
Во времена, когда не было мощных цифровых компьютеров, Карл Пирсон точно рассчитал дальнейшие границы, [31] [20] например, отделив «U-образные» от «J-образных» распределений. Нижняя граница (избыточный эксцесс + 2 − асимметрия 2 = 0) создается асимметричными «U-образными» бета-распределениями с обоими значениями параметров формы α и β, близкими к нулю. Верхняя граница (избыточный эксцесс − (3/2) асимметрия 2 = 0) создается крайне асимметричными распределениями с очень большими значениями одного из параметров и очень малыми значениями другого параметра. Карл Пирсон показал [20] что эта верхняя граница (избыточный эксцесс − (3/2) асимметрия 2 = 0) также является пересечением с распределением Пирсона III, которое имеет неограниченную поддержку в одном направлении (в сторону положительной бесконечности) и может иметь колоколообразную или J-образную форму. Его сын, Эгон Пирсон , показал [30] что область (в плоскости эксцесса/квадратной асимметрии), занятая бета-распределением (эквивалентно распределению Пирсона I), приближается к этой границе (избыточный эксцесс - (3/2) асимметрия 2 = 0) разделяется с нецентральным распределением хи-квадрат . Карл Пирсон [32] (Пирсон 1895, стр. 357, 360, 373–376) также показал, что гамма-распределение представляет собой распределение Пирсона типа III. Следовательно, эта граничная линия распределения Пирсона типа III известна как гамма-линия. (Это можно показать из того факта, что избыточный эксцесс гамма-распределения равен 6/ k , а квадрат асимметрии равен 4/ k , следовательно (избыточный эксцесс − (3/2) асимметрия 2 = 0) тождественно удовлетворяется гамма-распределением независимо от значения параметра «k»). Позже Пирсон заметил, что распределение хи-квадрат является частным случаем типа III Пирсона и также разделяет эту граничную линию (как это видно из того факта, что для распределения хи-квадрат избыточный эксцесс равен 12/ k , а квадрат асимметрия равна 8/ k , следовательно (избыточный эксцесс − (3/2) асимметрия 2 = 0) выполняется одинаково независимо от значения параметра «k»). Этого и следовало ожидать, поскольку распределение хи-квадрат X ~ χ 2 ( k ) является частным случаем гамма-распределения с параметризацией X ~ Γ(k/2, 1/2), где k — положительное целое число, которое определяет «количество степеней свободы» распределения хи-квадрат.
Пример бета-распределения вблизи верхней границы (избыточный эксцесс - (3/2) асимметрия 2 = 0) определяется соотношением α = 0,1, β = 1000, для которого соотношение (избыточный эксцесс)/(асимметрия 2 ) = 1,49835 приближается к верхнему пределу 1,5 снизу. Пример бета-распределения вблизи нижней границы (избыточный эксцесс + 2 − асимметрия 2 = 0) определяется как α= 0,0001, β = 0,1, для которых значения выражения (эксцесс + 2)/(асимметрия 2 ) = 1,01621 приближается к нижнему пределу 1 сверху. В бесконечно малом пределе, когда α и β симметрично приближаются к нулю, избыточный эксцесс достигает минимального значения при −2. Это минимальное значение возникает в точке, в которой нижняя граничная линия пересекает вертикальную ось ( ординату ). (Однако в исходной диаграмме Пирсона ордината представляет собой эксцесс, а не избыточный эксцесс, и она увеличивается вниз, а не вверх).
Значения асимметрии и избыточного эксцесса ниже нижней границы (избыточный эксцесс + 2 – асимметрия 2 = 0) не может произойти ни при каком распределении, и поэтому Карл Пирсон правильно назвал область ниже этой границы «невозможной областью». Граница этой «невозможной области» определяется (симметричными или асимметричными) бимодальными U-образными распределениями, для которых параметры α и β приближаются к нулю и, следовательно, вся плотность вероятности сосредоточена на концах: x = 0, 1 практически без ничего. между ними. Поскольку при α ≈ β ≈ 0 плотность вероятности сосредоточена на двух концах x = 0 и x = 1, эта «невозможная граница» определяется распределением Бернулли , где два единственно возможных результата происходят с соответствующими вероятностями p и q = 1- п . Для случаев, приближающихся к этой предельной границе с симметрией α = β, асимметрия ≈ 0, избыточный эксцесс ≈ -2 (это наименьший возможный избыточный эксцесс для любого распределения), а вероятности p ≈ q ≈ 1/2. Для случаев, приближающихся к этой предельной границе с асимметрией, избыточный эксцесс ≈ −2 + асимметрия 2 , а плотность вероятности сконцентрирована больше на одном конце, чем на другом (практически ничего между ними), с вероятностями на левом конце x = 0 и на правом конце x = 1.
Симметрия [ править ]
Все утверждения условны при α , β > 0:
- функции плотности вероятности Симметрия отражения
- Кумулятивная функция распределения, симметрия отражения плюс унитарный сдвиг
- моды Симметрия отражения плюс унитарный перевод
- Средняя симметрия отражения плюс унитарный перевод
- Каждый из геометрических средств применяется следующая симметрия: асимметричен по отдельности, между средним геометрическим, основанным на X , и средним геометрическим, основанным на его отражении (1-X),
- Гармоничное означает, что применяется следующая симметрия: каждый из них индивидуально асимметричен; между средним гармоническим значением, основанным на X , и средним гармоническим значением, основанным на его отражении (1-X),
- .
- Дисперсионная симметрия
- Каждое геометрическое отклонение применяется следующая симметрия: индивидуально асимметрично, между логарифмическим геометрическим отклонением, основанным на X, и логарифмическим геометрическим отклонением, основанным на его отражении (1-X),
- Геометрическая ковариационная симметрия
- Среднее абсолютное отклонение от средней симметрии
- асимметрия
- Избыточная симметрия эксцесса
- характеристической функции Симметрия действительной части (относительно начала координат переменной «t»)
- Характеристическая функция кососимметрии мнимой части (относительно начала координат переменной «t»)
- характеристической функции Симметрия абсолютного значения (относительно начала переменной «t»)
- Дифференциальная энтропийная симметрия
- Относительная энтропия (также называемая дивергенцией Кульбака – Лейблера ) симметрия
- информационной матрицы Фишера Симметрия
Геометрия функции плотности вероятности [ править ]
Точки перегиба [ править ]

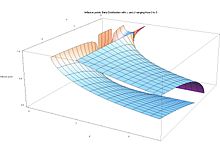
При определенных значениях параметров формы α и β функция плотности вероятности имеет точки перегиба , в которых кривизна меняет знак. Положение этих точек перегиба может быть полезно в качестве меры дисперсии или распространения распределения.
Определение следующей величины:
Возникают точки перегиба, [1] [7] [8] [19] в зависимости от значения параметров формы α и β следующим образом:
- (α > 2, β > 2) Распределение колоколообразное (симметричное при α = β и перекошенное в противном случае) с двумя точками перегиба , равноудаленными от моды:
- (α = 2, β > 2) Распределение унимодальное, положительно асимметричное, правостороннее, с одной точкой перегиба , расположенной справа от моды:
- (α > 2, β = 2) Распределение унимодальное, отрицательно асимметричное, левостороннее, с одной точкой перегиба , расположенной левее моды:
- (1 < α < 2, β > 2, α+β>2) Распределение унимодальное, положительно асимметричное, правостороннее, с одной точкой перегиба , расположенной справа от моды:
- (0 < α < 1, 1 < β < 2) Распределение имеет моду на левом конце x = 0 и имеет положительную асимметрию, правостороннюю. Есть одна точка перегиба , расположенная справа от режима:
- (α > 2, 1 < β < 2) Распределение унимодальное, отрицательно перекошенное, левостороннее, с одной точкой перегиба , расположенной слева от моды:
- (1 < α < 2, 0 < β < 1) Распределение имеет моду на правом конце x = 1 и имеет отрицательный перекос, левосторонний. Есть одна точка перегиба , расположенная слева от моды:
В остальных (симметричных и перекошенных) областях точек перегиба нет: П-образная: (α, β < 1) перевернутая-П-образная: (1 < α < 2, 1 < β < 2), обратная- J-образный (α < 1, β > 2) или J-образный: (α > 2, β < 1)
На прилагаемых графиках показаны местоположения точек перегиба (показаны вертикально в диапазоне от 0 до 1) в зависимости от α и β (горизонтальные оси в диапазоне от 0 до 5). На поверхностях, пересекающих линии α = 1, β = 1, α = 2 и β = 2, имеются большие разрезы, поскольку при этих значениях бета-распределение меняется от 2 мод к 1 моде и к отсутствию моды.
Формы [ править ]





Функция бета-плотности может принимать самые разные формы в зависимости от значений двух параметров α и β . Способность бета-распределения принимать такое большое разнообразие форм (с использованием только двух параметров) отчасти объясняет его широкое применение для моделирования реальных измерений:
Симметричный ( α = β ) [ править ]
- функция плотности симметрична примерно 1/2 (синие и бирюзовые графики).
- медиана = среднее значение = 1/2.
- асимметрия = 0.
- дисперсия = 1/(4(2α + 1))
- α = β < 1
- U-образный (синий участок).
- бимодальный: левый режим = 0, правый режим = 1, антирежим = 1/2
- 1/12 < вар( X ) < 1/4 [1]
- −2 < избыточный эксцесс ( X ) < −6/5
- α = β = 1/2 — арксинусное распределение
- вар( X ) = 1/8
- избыточный эксцесс ( X ) = -3/2
- CF = Ринк (т) [33]
- α = β → 0 представляет собой 2-точечное распределение Бернулли с равной вероятностью 1/2 на каждом дельта-функции Дирака конце x = 0 и x = 1 и нулевой вероятностью во всех остальных местах. Подбрасывание монеты: одна грань монеты равна х = 0, а другая сторона — х = 1.
- более низкое значение, чем это, невозможно достичь ни для одного распределения.
- Дифференциальная энтропия приближается к минимальному значению −∞.
- α = β = 1
- равномерное распределение [0, 1]
- нет режима
- вар( X ) = 1/12
- избыточный эксцесс ( X ) = −6/5
- (отрицательная где-либо еще) Дифференциальная энтропия достигает максимального значения, равного нулю.
- CF = Синк (т)
- α = β > 1
- симметричный унимодальный
- режим = 1/2.
- 0 <вар( X ) < 1/12 [1]
- −6/5 < избыточный эксцесс ( X ) < 0
- α = β = 3/2 — полуэллиптическое [0, 1] распределение, см.: Распределение полукруга Вигнера. [34]
- вар( X ) = 1/16.
- избыточный эксцесс ( X ) = -1
- CF = 2 Джинч (т)
- α = β = 2 — параболическое [0, 1] распределение
- где( X ) = 1/20
- избыточный эксцесс ( X ) = -6/7
- CF = 3 у меня есть (т) [35]
- α = β > 2 имеет колоколообразную форму с точками перегиба , расположенными по обе стороны от моды.
- 0 <вар( X ) < 1/20
- −6/7 < избыточный эксцесс ( X ) < 0
- α = β → ∞ представляет собой 1-точечное вырожденное распределение с пиком дельта-функции Дирака в средней точке x = 1/2 с вероятностью 1 и нулевой вероятностью во всех остальных местах. Существует 100% вероятность (абсолютная уверенность), сосредоточенная в одной точке x = 1/2.
- Дифференциальная энтропия приближается к минимальному значению −∞.
Перекошенный ( α ≠ β ) [ править ]
Функция плотности искажена . Перестановка значений параметров дает зеркальное отображение (обратное) исходной кривой, в некоторых более частных случаях:
- α < 1, β < 1
- U-образный
- Положительный перекос для α < β, отрицательный перекос для α > β.
- бимодальный: левый режим = 0, правый режим = 1, антирежим =
- 0 < медиана < 1.
- 0 <вар( X ) < 1/4
- а > 1, б > 1
- унимодальный (пурпурный и голубой графики),
- Положительный перекос для α < β, отрицательный перекос для α > β.
- 0 < медиана < 1
- 0 <вар( X ) < 1/12
- α < 1, β ≥ 1
- обратная J-образная форма с правым хвостом,
- положительно перекошенный,
- строго убывающая, выпуклая
- режим = 0
- 0 < медиана < 1/2.
- (максимальная дисперсия наблюдается для , или α = Φ сечение сопряженное золотое )
- α ≥ 1, β < 1
- J-образный с левым хвостовиком,
- отрицательно перекошенный,
- строго возрастающая, выпуклая
- режим = 1
- 1/2 < медиана < 1
- (максимальная дисперсия наблюдается для , или β = Φ сечение сопряженное золотое )
- α = 1, β > 1
- положительно перекошенный,
- строго убывающая (красный график),
- обратное (зеркальное) распределение степенной функции [0,1]
- среднее = 1/(β + 1)
- медиана = 1 - 1/2 1/б
- режим = 0
- α = 1, 1 < β < 2
- вогнутый
- 1/18 < вар( X ) < 1/12.
- а = 1, б = 2
- прямая линия с наклоном −2, право- треугольное распределение с прямым углом на левом конце, при x = 0
- где( Х ) = 1/18
- α = 1, β > 2
- обратная J-образная форма с правым хвостом,
- выпуклый
- 0 <вар( X ) < 1/18
- α > 1, β = 1
- отрицательно перекошенный,
- строго возрастающая (зеленый участок),
- распределение степенной функции [0, 1] [8]
- среднее значение = α/(α + 1)
- медиана = 1/2 1/а
- режим = 1
- 2 > а > 1, б = 1
- вогнутый
- 1/18 < вар( X ) < 1/12
- а = 2, б = 1
- прямая с наклоном +2, право- треугольное распределение с прямым углом на правом конце, при x = 1
- где( Х ) = 1/18
- а > 2, б = 1
- J-образная с левым хвостиком, выпуклая
- 0 <вар( X ) < 1/18
Связанные дистрибутивы [ править ]
Трансформации [ править ]
- Если X ~ Beta( α , β ), то 1 − X ~ Beta( β , α ) зеркальная симметрия
- Если X ~ Beta( α , β ), то . Бета -распределение простых чисел , также называемое «бета-распределением второго рода».
- Если , затем имеет обобщенное логистическое распределение с плотностью , где это логистическая сигмоида .
- Если X ~ Beta( α , β ), то .
- Если X ~ Beta( n /2, m /2), то (при условии, что n > 0 и m > 0), F-распределение Фишера-Снедекора .
- Если тогда min + X (max − min) ~ PERT(min, max, m , λ ), где PERT обозначает распределение PERT , используемое в анализе PERT , а m = наиболее вероятное значение. [36] Традиционно [37] λ = 4 в анализе PERT.
- Если X ~ Beta(1, β ), то X ~ распределение Кумарасвами с параметрами (1, β )
- Если X ~ Beta( α , 1), то X ~ распределение Кумарасвами с параметрами ( α , 1)
- Если X ~ Beta( α , 1), то −ln( X ) ~ Экспонента( α )
Особые и предельные случаи [ править ]

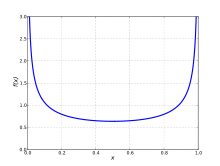
- Бета(1, 1) ~ U(0, 1) с плотностью 1 на этом интервале.
- Beta(n, 1) ~ Максимум из n независимых случайных величин. с U(0, 1) , иногда называемое стандартным распределением степенной функции с плотностью n x п –1 на этом интервале.
- Beta(1, n) ~ Минимум n независимых случайных величин. с U(0, 1) с плотностью n (1 - x ) п -1 на этом интервале.
- Если X ~ Beta(3/2, 3/2) и r > 0, то 2 rX − r ~ полукруговое распределение Вигнера .
- Бета(1/2, 1/2) эквивалентна распределению арксинуса . Это распределение также является априорной вероятностью Джеффри для распределения Бернулли и биномиального распределения . Арксинусная плотность вероятности — это распределение, которое фигурирует в нескольких фундаментальных теоремах о случайном блуждании. при честном подбрасывании монеты В случайном блуждании вероятность момента последнего посещения источника распределяется как (U-образное) арксинусное распределение . [5] [11] В игре с честным подбрасыванием монеты для двух игроков говорят, что игрок лидирует, если случайное блуждание (которое началось в начале координат) находится выше начала координат. , когда данный игрок будет лидировать в игре продолжительностью 2 N , не равно N. Наиболее вероятное количество раз Напротив, N — это наименее вероятное количество раз, когда игрок будет лидировать. Наиболее вероятное количество раз в лидерстве — 0 или 2 N (следуя арксинусному распределению ).
- экспоненциальное распределение .
- гамма -распределение .
- Для больших , нормальное распределение . Точнее, если затем сходится по распределению к нормальному распределению со средним значением 0 и дисперсией по мере увеличения n .
Получено из других дистрибутивов [ править ]
- Статистика k - го порядка выборки размера n из равномерного распределения представляет собой бета-случайную величину U ( k ) ~ Beta( k , n +1− k ). [38]
- Если X ~ Gamma(α, θ) и Y ~ Gamma(β, θ) независимы, то .
- Если и независимы, то .
- Если X ~ U(0, 1) и α > 0, то X 1/ а ~ Бета( α , 1). Распределение степенной функции.
- Если [ нужны разъяснения ] , затем [ нужны разъяснения ] для дискретных значений n и k, где и . [39]
- Если X ~ Коши(0, 1), то
Комбинация с другими дистрибутивами [ править ]
- X ~ Beta( α , β ) и Y ~ F(2 β , 2 α ), тогда для всех х > 0.
Объединение с другими дистрибутивами [ править ]
- Если p ~ Beta(α, β) и X ~ Bin( k , p ), то X ~ бета-биномиальное распределение
- Если p ~ Beta(α, β) и X ~ NB( r , p ), то X ~ бета отрицательное биномиальное распределение .
Обобщения [ править ]
- Обобщение на несколько переменных, то есть многомерное бета-распределение , называется распределением Дирихле . Одномерные маргинальные значения распределения Дирихле имеют бета-распределение. Бета-распределение сопряжено с биномиальным распределением и распределением Бернулли точно так же, как распределение Дирихле сопряжено с полиномиальным распределением и категориальным распределением .
- Распределение Пирсона типа I идентично бета-распределению (за исключением произвольного сдвига и изменения масштаба, которые также могут быть выполнены с помощью параметризации бета-распределения с четырьмя параметрами).
- Бета-распределение — это частный случай нецентрального бета-распределения , где : .
- Обобщенное бета-распределение представляет собой семейство распределений с пятью параметрами, в котором бета-распределение является частным случаем.
- — Бета-распределение матричной переменной это распределение положительно определенных матриц .
Статистический вывод
Оценка параметров [ править ]
Метод моментов [ править ]
Два неизвестных параметра [ править ]
Два неизвестных параметра ( бета-распределения, поддерживаемого в интервале [0,1]), можно оценить с помощью метода моментов с первыми двумя моментами (выборочное среднее и выборочная дисперсия) следующим образом. Позволять:
быть выборочной средней оценкой и
быть оценкой выборочной дисперсии . методом моментов Оценки параметров имеют вид
- если
- если
Если распределение требуется в известном интервале, отличном от [0, 1] со случайной величиной X , скажем, [ a , c ] со случайной величиной Y , замените с и с в приведенной выше паре уравнений для параметров формы (см. раздел «Четыре неизвестных параметра» ниже), [40] где:
Четыре неизвестных параметра [ править ]

Все четыре параметра ( бета-распределения, поддерживаемого в интервале [ a , c ], см. раздел «Альтернативные параметризации, Четыре параметра» ) можно оценить, используя метод моментов, разработанный Карлом Пирсоном , путем приравнивания выборочных и популяционных значений первых четырех центральных моментов. (среднее значение, дисперсия, асимметрия и избыточный эксцесс). [1] [41] [42] Избыточный эксцесс выражался через квадрат асимметрии и размер выборки ν = α + β (см. предыдущий раздел «Куртозис» ) следующим образом:
Это уравнение можно использовать для определения размера выборки ν = α + β с точки зрения квадрата асимметрии и избыточного эксцесса следующим образом: [41]
Это отношение (умноженное на коэффициент 3) между ранее полученными пределами границ бета-распределения в пространстве (как первоначально было сделано Карлом Пирсоном). [20] ) определяется координатами квадрата асимметрии по одной оси и избыточного эксцесса по другой оси (см. § Эксцесс, ограниченный квадратом асимметрии ):
Случай нулевой асимметрии можно решить сразу, поскольку при нулевой асимметрии α = β и, следовательно, ν = 2α = 2β, следовательно, α = β = ν/2.
(Избыточный эксцесс отрицательен для бета-распределения с нулевой асимметрией в диапазоне от -2 до 0, так что - и, следовательно, параметры формы образца - положительны и варьируются от нуля, когда параметры формы приближаются к нулю, а избыточный эксцесс приближается к -2, до бесконечности, когда параметры формы приближаются к бесконечности, а избыточный эксцесс приближается к нулю).
Для ненулевой асимметрии выборки необходимо решить систему двух связанных уравнений. Поскольку асимметрия и избыточный эксцесс не зависят от параметров , параметры может быть однозначно определена на основе асимметрии выборки и избыточного эксцесса выборки путем решения связанных уравнений с двумя известными переменными (асимметрия выборки и избыточный эксцесс выборки) и двумя неизвестными (параметрами формы):
в результате получается следующее решение: [41]
Где следует принять решения следующим образом: для (отрицательной) асимметрии выборки < 0 и для (положительной) асимметрии выборки > 0.
На прилагаемом графике эти два решения показаны как поверхности в пространстве с горизонтальными осями (эксцесс выборки) и (квадрат асимметрии выборки), а параметры формы - как вертикальная ось. Поверхности ограничены условием, что избыточный эксцесс выборки должен ограничиваться квадратом асимметрии выборки, как это предусмотрено в приведенном выше уравнении. Две поверхности встречаются у правого края, определяемого нулевой асимметрией. Вдоль этого правого края оба параметра равны, и распределение имеет симметричную U-образную форму для α = β < 1, равномерную для α = β = 1, перевернутую U-образную для 1 < α = β < 2 и колоколообразную форму. имеют форму для α = β > 2. Поверхности сходятся также у переднего (нижнего) края, определяемого линией «невозможной границы» (избыточный эксцесс + 2 – асимметрия 2 = 0). Вдоль этой передней (нижней) границы оба параметра формы приближаются к нулю, а плотность вероятности сконцентрирована больше на одном конце, чем на другом (практически ничего между ними), с вероятностями на левом конце x = 0 и на правом конце x = 1. Две поверхности становятся все дальше друг от друга по направлению к заднему краю. На этом заднем крае параметры поверхности сильно отличаются друг от друга. Как заметили, например, Боумен и Шентон, [43] выборка в окрестности линии (эксцесс выборки - (3/2)(асимметрия выборки) 2 = 0) (J-образная часть заднего края, где синий встречается с бежевым), «опасно близка к хаосу», потому что на этой линии знаменатель приведенного выше выражения для оценки ν = α + β становится нулевым и следовательно, ν приближается к бесконечности по мере приближения к этой линии. Боуман и Шентон [43] пишут, что «параметры более высокого момента (эксцесс и асимметрия) чрезвычайно хрупкие (около этой линии). Однако среднее и стандартное отклонение довольно надежны». Следовательно, проблема заключается в случае оценки четырех параметров для очень асимметричных распределений, когда избыточный эксцесс приближается к (3/2), умноженному на квадрат асимметрии. Эта граничная линия создается чрезвычайно асимметричными распределениями с очень большими значениями одного из параметров и очень маленькими значениями другого параметра. асимметрия ) Численный пример см. в § Эксцесс, ограниченный квадратом асимметрии, а также дополнительные комментарии об этой граничной линии заднего края (выборочный избыточный эксцесс - (3/2) (выборочная 2 = 0). Как заметил сам Карл Пирсон [44] этот вопрос может не иметь большого практического значения, поскольку эта проблема возникает только для очень асимметричных J-образных (или зеркальных J-образных) распределений с очень разными значениями параметров формы, которые вряд ли будут часто встречаться на практике). Обычные распределения в форме перекошенного колокола, встречающиеся на практике, не имеют этой проблемы оценки параметров.
Остальные два параметра может быть определен с использованием выборочного среднего и выборочной дисперсии с использованием различных уравнений. [1] [41] Одной из альтернатив является расчет диапазона интервала поддержки. на основе выборочной дисперсии и выборочного эксцесса. Для этого можно решить в терминах диапазона , уравнение, выражающее избыточный эксцесс через выборочную дисперсию, и размер выборки ν (см. § Эксцесс и § Альтернативные параметризации, четыре параметра ):
чтобы получить:
Другой альтернативой является расчет диапазона интервала поддержки. на основе выборочной дисперсии и асимметрии выборки. [41] Для этого можно решить в терминах диапазона , уравнение, выражающее квадрат асимметрии через выборочную дисперсию, и размер выборки ν (см. разделы «Асимметрия» и «Альтернативные параметризации, четыре параметра»):
чтобы получить: [41]
Оставшийся параметр можно определить из выборочного среднего и ранее полученных параметров: :
и, наконец, .
В приведенных выше формулах в качестве оценок выборочных моментов можно принять, например:
Оценщики G 1 для асимметрии выборки и G 2 для эксцесса выборки используются DAP / SAS , PSPP / SPSS и Excel . Однако они не используются БМДП и (по данным [45] ) они не использовались MINITAB в 1998 году. На самом деле, Джоанс и Гилл в своем исследовании 1998 года [45] пришли к выводу, что оценки асимметрии и эксцесса, используемые в BMDP и в MINITAB (на тот момент), имели меньшую дисперсию и среднеквадратическую ошибку в нормальных выборках, но оценки асимметрии и эксцесса, используемые в DAP / SAS , PSPP / SPSS , а именно G 1 и G 2 имел меньшую среднеквадратическую ошибку в выборках с очень асимметричным распределением. Именно по этой причине мы указали «асимметрию выборки» и т. д. в приведенных выше формулах, чтобы было ясно, что пользователь должен выбрать лучшую оценку в соответствии с рассматриваемой проблемой, как лучшую оценку асимметрии и эксцесса. зависит от степени асимметрии (как показали Джоэнс и Гилл [45] ).
Максимальная вероятность [ править ]
Два неизвестных параметра [ править ]

Как и в случае оценок максимального правдоподобия для гамма-распределения , оценки максимального правдоподобия для бета-распределения не имеют общего решения в замкнутой форме для произвольных значений параметров формы. Если X 1 , ..., X N являются независимыми случайными величинами, каждая из которых имеет бета-распределение, совместная логарифмическая функция правдоподобия для N iid наблюдений равна:
Нахождение максимума по параметру формы включает в себя взятие частной производной по параметру формы и установку выражения, равного нулю, что дает оценку максимального правдоподобия параметров формы:
где:
поскольку дигамма-функция, обозначаемая ψ(α), определяется как логарифмическая производная гамма -функции : [17]
Чтобы гарантировать, что значения с нулевым наклоном тангенса действительно являются максимальными (а не седловой точкой или минимумом), необходимо также удовлетворить условие, что кривизна отрицательна. Это равнозначно удовлетворению того, что вторая частная производная по параметрам формы отрицательна.
используя предыдущие уравнения, это эквивалентно:
где тригамма-функция , обозначаемая ψ 1 ( α ), является второй из полигамма-функций и определяется как производная дигамма- функции:
Эти условия эквивалентны утверждению, что дисперсии логарифмически преобразованных переменных положительны, поскольку:
Поэтому условие отрицательной кривизны в максимуме эквивалентно утверждениям:
Альтернативно, условие отрицательной кривизны в максимуме также эквивалентно утверждению, что следующие логарифмические производные средних геометрических G X и G ( 1−X) положительны, поскольку:
Хотя эти наклоны действительно положительны, другие наклоны отрицательны:
Наклоны среднего и медианы по отношению к α и β демонстрируют схожее знаковое поведение.
Из условия, что в максимуме частная производная по параметру формы равна нулю, мы получаем следующую систему связанных уравнений оценки максимального правдоподобия (для среднего логарифмического правдоподобия), которую необходимо инвертировать, чтобы получить (неизвестное) оценки параметров формы в терминах (известного) среднего логарифмов выборок X 1 , ..., X N : [1]
где мы признаем как логарифм выборочного среднего геометрического и как логарифм выборочного среднего геометрического на основе (1 - X зеркального отображения X. ) , Для , отсюда следует, что .
Эти связанные уравнения, содержащие дигамма-функции оценок параметров формы. необходимо решать численными методами, как это сделано, например, Бекманом и др. [46] Гнанадэсикан и др. дать численные решения для некоторых случаев. [47] Н.Л.Джонсон и С.Коц [1] предполагают, что для «не слишком малых» оценок параметров формы , логарифмическое приближение дигамма-функции может использоваться для получения начальных значений для итеративного решения, поскольку уравнения, полученные в результате этого приближения, могут быть решены точно:
что приводит к следующему решению для начальных значений (оценочных параметров формы в терминах выборочных средних геометрических) для итеративного решения:
Альтернативно, оценки, полученные методом моментов, могут вместо этого использоваться в качестве начальных значений для итеративного решения связанных уравнений максимального правдоподобия в терминах дигамма-функций.
Если распределение требуется в известном интервале, отличном от [0, 1] со случайной величиной X , скажем, [ a , c ] со случайной величиной Y , тогда замените ln( X i ) в первом уравнении на
- ,
и заменим ln(1− X i ) во втором уравнении на
(см. раздел «Альтернативные параметризации, четыре параметра» ниже).
Если известен один из параметров формы, задача значительно упрощается. Следующее логит- преобразование можно использовать для определения неизвестного параметра формы (для асимметричных случаев, таких как , в противном случае, если они симметричны, оба равных параметра известны, если известен один):
Это логит- преобразование представляет собой логарифм преобразования, которое делит переменную X на ее зеркальное отображение ( X /(1 - X ), что приводит к «перевернутому бета-распределению» или простому бета-распределению (также известному как бета-распределение второго рода или Тип VI Пирсона ) с носителем [0, +∞). Как обсуждалось ранее в разделе «Моменты логарифмически преобразованных случайных величин», логит- преобразование , изученный Джонсоном, [24] расширяет конечный носитель [0, 1] на основе исходной переменной X до бесконечного носителя в обоих направлениях вещественной линии (−∞, +∞).
Если, например, известен, неизвестный параметр можно получить с помощью обратного [48] дигамма-функция правой части этого уравнения:
В частности, если один из параметров формы имеет значение единицы, например для (распределение степенной функции с ограниченным носителем [0,1]), используя тождество ψ( x + 1) = ψ( x ) + 1/ x в уравнении , оценка максимального правдоподобия для неизвестного параметра является, [1] точно:
Бета-версия имеет поддержку [0, 1], поэтому , и, следовательно, , и поэтому
В заключение, оценки максимального правдоподобия параметров формы бета-распределения (в общем) являются сложной функцией выборочного среднего геометрического и выборочного среднего геометрического , основанного на (1-X) , зеркальном отображении X . Можно спросить: если дисперсия (помимо среднего) необходима для оценки двух параметров формы методом моментов, то почему (логарифмическая или геометрическая) дисперсия не необходима для оценки двух параметров формы методом максимального правдоподобия, поскольку для чего достаточно только геометрических средств? Ответ в том, что среднее значение не дает столько информации, сколько среднее геометрическое. Для бета-распределения с равными параметрами формы α = β среднее значение равно ровно 1/2, независимо от значения параметров формы и, следовательно, независимо от значения статистической дисперсии (дисперсии). С другой стороны, среднее геометрическое бета-распределения с равными параметрами формы α = β зависит от значения параметров формы и, следовательно, содержит больше информации. Кроме того, среднее геометрическое бета-распределения не удовлетворяет условиям симметрии, которым удовлетворяет среднее значение, поэтому, используя как среднее геометрическое, основанное на X и среднее геометрическое на основе (1 - X ), метод максимального правдоподобия способен обеспечить наилучшие оценки для обоих параметров α = β без необходимости использования дисперсии.
Можно выразить совместную логарифмическую вероятность на N iid наблюдений через достаточную статистику (средние геометрические выборки) следующим образом:
Мы можем построить график совместного логарифма правдоподобия на N наблюдений для фиксированных значений выборочных средних геометрических значений, чтобы увидеть поведение функции правдоподобия в зависимости от параметров формы α и β. На таком графике средства оценки параметров формы соответствуют максимумам функции правдоподобия. См. прилагаемый график, который показывает, что все функции правдоподобия пересекаются при α = β = 1, что соответствует значениям параметров формы, которые дают максимальную энтропию (максимальная энтропия возникает для параметров формы, равных единице: равномерное распределение). Из графика видно, что функция правдоподобия дает резкие пики для значений оценщиков параметров формы, близких к нулю, но что для значений оценщиков параметров формы больше единицы функция правдоподобия становится совершенно плоской с менее выраженными пиками. Очевидно, что метод оценки параметра максимального правдоподобия для бета-распределения становится менее приемлемым для больших значений оценщиков параметра формы, поскольку неопределенность в определении пика увеличивается со значением оценщиков параметра формы. К тому же выводу можно прийти, заметив, что кривизна функции правдоподобия выражается через геометрические дисперсии
Эти дисперсии (и, следовательно, кривизны) намного больше при малых значениях параметров формы α и β. Однако для значений параметров формы α, β > 1 дисперсии (и, следовательно, кривизны) выравниваются. Эквивалентно этот результат следует из границы Крамера-Рао , поскольку компоненты информационной матрицы Фишера для бета-распределения представляют собой эти логарифмические дисперсии. Граница Крамера – Рао утверждает, что дисперсия любой несмещенной оценки α ограничено обратной величиной информации Фишера :
поэтому дисперсия оценок увеличивается с увеличением α и β, поскольку логарифмические дисперсии уменьшаются.
Также можно выразить совместное логарифмическое правдоподобие на N iid наблюдений через выражения дигамма-функции для логарифмов выборочных средних геометрических значений следующим образом:
это выражение идентично отрицательному значению перекрестной энтропии (см. раздел «Количество информации (энтропия)»). Следовательно, нахождение максимума совместной логарифмической вероятности параметров формы по наблюдениям N iid идентично нахождению минимума перекрестной энтропии для бета-распределения как функции параметров формы.
с перекрестной энтропией, определяемой следующим образом:
Четыре неизвестных параметра [ править ]
Процедура аналогична той, которая применяется в случае двух неизвестных параметров. Если Y 1 , ..., Y N являются независимыми случайными величинами, каждая из которых имеет бета-распределение с четырьмя параметрами, совместная логарифмическая функция правдоподобия для N iid наблюдений равна:
Нахождение максимума по параметру формы включает в себя взятие частной производной по параметру формы и установку выражения, равного нулю, что дает оценку максимального правдоподобия параметров формы:
эти уравнения можно переформулировать в следующую систему из четырех связанных уравнений (первые два уравнения представляют собой средние геометрические, а вторые два уравнения представляют собой гармонические средние) с точки зрения оценок максимального правдоподобия для четырех параметров :
с выборочными геометрическими средними:
Параметры вложены в выражения среднего геометрического нелинейным образом (в степени 1/ N ). Это, как правило, исключает решение в замкнутой форме, даже для аппроксимации начального значения в целях итерации. Одной из альтернатив является использование в качестве начальных значений для итерации значений, полученных методом решения метода моментов для случая четырех параметров. Более того, выражения для гармонических средних четко определены только для , что исключает решение максимального правдоподобия для параметров формы меньше единицы в случае с четырьмя параметрами. Информационная матрица Фишера для случая с четырьмя параметрами положительно определена только для α, β > 2 (более подробное обсуждение см. в разделе «Информационная матрица Фишера, случай с четырьмя параметрами»), для колоколообразных (симметричных или несимметричных) бета-распределений с перегибом точки, расположенные по обе стороны от моды. Следующие информационные компоненты Фишера (которые представляют собой ожидания кривизны логарифмической функции правдоподобия) имеют особенности при следующих значениях:
(подробнее см. раздел «Информационная матрица Фишера»). Таким образом, невозможно строго выполнить оценку максимального правдоподобия для некоторых хорошо известных распределений, принадлежащих к семейству четырехпараметрических бета-распределений, таких как равномерное распределение (Beta (1, 1, a , c )) и арксинусное распределение . (Бета(1/2, 1/2, а , с )). Н.Л.Джонсон и С.Коц [1] игнорировать уравнения для гармонических средних и вместо этого предложить: «Если a и c неизвестны, и оценки максимального правдоподобия a , c требуются , α и β, описанная выше процедура (для случая двух неизвестных параметров, с X, преобразованным как X = ( Y − a )/( c − a )) можно повторить, используя последовательность пробных значений a и c , пока пара ( a , c ), для которой максимальное правдоподобие (при данных a и c ) не станет максимально возможным, достигается» (где для ясности их обозначения параметров переведены в настоящие обозначения).
матрица Информационная Фишера
Пусть случайная величина X имеет плотность вероятности f ( x ; α ). Частная производная по (неизвестному и подлежащему оценке) параметру логарифмической функции правдоподобия называется оценкой . Второй момент партитуры называется информацией Фишера :
Ожидание нулю , оценки равно поэтому информация Фишера также является вторым моментом, сосредоточенным на среднем значении оценки: дисперсии оценки .
Если логарифмическая функция правдоподобия дважды дифференцируема по параметру α и при определенных условиях регулярности: [49] тогда информацию Фишера можно также записать следующим образом (часто это более удобная форма для расчетов):
Таким образом, информация Фишера представляет собой отрицательное математическое ожидание второй производной по отношению к параметру α логарифмической функции правдоподобия . Следовательно, информация Фишера является мерой кривизны логарифмической функции правдоподобия α. Низкая кривизна (и, следовательно, большой радиус кривизны ), более плоская логарифмическая кривая функции правдоподобия имеет низкую информацию Фишера; в то время как логарифмическая кривая функции правдоподобия с большой кривизной (и, следовательно, с низким радиусом кривизны ) имеет высокую информацию Фишера. Когда информационная матрица Фишера вычисляется при оценках параметров («наблюдаемая информационная матрица Фишера»), это эквивалентно замене истинной логарифмической поверхности правдоподобия аппроксимацией ряда Тейлора, с учетом квадратичных членов. [50] Слово «информация» в контексте информации Фишера относится к информации о параметрах. Такая информация, как: оценка, достаточность и свойства дисперсий оценок. Граница Крамера -Рао утверждает, что обратная информация Фишера является нижней границей дисперсии любой оценки параметра α:
Точность, с которой можно оценить оценку параметра α, ограничена информацией Фишера логарифмической функции правдоподобия. Информация Фишера является мерой минимальной ошибки, связанной с оценкой параметра распределения, и ее можно рассматривать как меру разрешающей способности эксперимента, необходимой для различения двух альтернативных гипотез параметра. [51]
Когда есть N параметров
тогда информация Фишера принимает форму размера N × N положительной полуопределенной симметричной матрицы , информационной матрицы Фишера, с типичным элементом:
При определенных условиях регулярности [49] Информационная матрица Фишера также может быть записана в следующей форме, которая часто более удобна для вычислений:
Используя X 1 , ..., X N , случайные величины N можно построить -мерную «коробку» со сторонами X 1 , ..., X N . Коста и Кавер [52] показывают, что дифференциальная энтропия (Шеннона) h ( X ) связана с объемом типичного набора (имея энтропию выборки, близкую к истинной энтропии), тогда как информация Фишера связана с поверхностью этого типичного набора.
Два параметра [ править ]
Для независимых случайных величин X 1 , ..., X N, каждая из которых имеет бета-распределение, параметризованное параметрами формы α и β , совместная логарифмическая функция правдоподобия для N iid наблюдений равна:
следовательно, совместная логарифмическая функция правдоподобия по N iid наблюдениям равна
В случае двух параметров информация Фишера имеет 4 компонента: 2 диагональных и 2 недиагональных. Поскольку информационная матрица Фишера симметрична, один из этих недиагональных компонентов независим. Следовательно, информационная матрица Фишера имеет 3 независимых компонента (2 диагональных и 1 недиагональный).
Арьял и Надараджа [53] рассчитана информационная матрица Фишера для случая с четырьмя параметрами, из которой случай с двумя параметрами может быть получен следующим образом:
Поскольку информационная матрица Фишера симметрична
Информационные компоненты Фишера равны логарифмической геометрической дисперсии и логарифмической геометрической ковариации. Следовательно, их можно выразить в виде тригамма-функций , обозначаемых ψ 1 (α), второй из полигамма-функций , определяемой как производная дигамма- функции:
Эти производные также получены в разделе § Два неизвестных параметра , и в этом разделе также показаны графики логарифмической функции правдоподобия. § Геометрическая дисперсия и ковариация содержит графики и дальнейшее обсуждение компонентов информационной матрицы Фишера: логарифмических геометрических дисперсий и логарифмической геометрической ковариации как функции параметров формы α и β. § Моменты логарифмически преобразованных случайных величин содержит формулы для моментов логарифмически преобразованных случайных величин. Изображения для информационных компонентов Fisher и показаны в § Геометрическая дисперсия .
Представляет интерес определитель информационной матрицы Фишера (например, для расчета априорной вероятности Джеффриса). Из выражений для отдельных компонентов информационной матрицы Фишера следует, что определитель информационной матрицы Фишера (симметричной) для бета-распределения равен:
Из критерия Сильвестра (проверка того, все ли диагональные элементы положительны) следует, что информационная матрица Фишера для случая с двумя параметрами является положительно определенной (при стандартном условии, что параметры формы положительны α > 0 и β > 0).
Четыре параметра [ править ]


Если Y 1 , ..., Y N — независимые случайные величины, каждая из которых имеет бета-распределение с четырьмя параметрами: показателями α и β , а также a (минимум диапазона распределения) и c (максимум диапазона распределения) ) (раздел «Альтернативные параметризации», «Четыре параметра»), с функцией плотности вероятности :
Совместная логарифмическая функция правдоподобия по N iid наблюдениям равна:
Для случая с четырьмя параметрами информация Фишера имеет 4*4=16 компонентов. Он имеет 12 недиагональных компонентов = (всего 4 × 4 — 4 диагонали). Поскольку информационная матрица Фишера симметрична, половина этих компонентов (12/2=6) независимы. Следовательно, информационная матрица Фишера имеет 6 независимых недиагональных + 4 диагонали = 10 независимых компонентов. Арьял и Надараджа [53] рассчитал информационную матрицу Фишера для случая с четырьмя параметрами следующим образом:
В приведенных выше выражениях использование X вместо Y в выражениях var[ln( X )] = ln(var GX ) не является ошибкой . Выражения в терминах логарифмических геометрических дисперсий и логарифмической геометрической ковариации возникают как функции двухпараметрической параметризации X ~ Beta( α , β ), потому что при взятии частных производных по показателям ( α , β ) в случае с четырьмя параметрами , можно получить те же выражения, что и для случая с двумя параметрами: эти члены четырехпараметрической информационной матрицы Фишера не зависят от минимума a и максимума c диапазона распределения. Единственным ненулевым членом при двойном дифференцировании логарифмической функции правдоподобия по показателям α и β является вторая производная логарифма бета-функции: ln(B( α , β )). Этот член не зависит от минимума a и максимума c диапазона распределения. Двойное дифференцирование этого члена приводит к тригамма-функциям. Об этом также свидетельствуют разделы «Максимальное правдоподобие», «Два неизвестных параметра» и «Четыре неизвестных параметра».
Информация Фишера для N i.id образцов в N раз превышает индивидуальную информацию Фишера (уравнение 11.279, стр. 394 книги Cover and Thomas). [27] ). (Арьял и Надараджа [53] возьмите одно наблюдение, N = 1, чтобы вычислить следующие компоненты информации Фишера, что приводит к тому же результату, что и рассмотрение производных логарифма правдоподобия на N наблюдений. Более того, ниже ошибочное выражение для в Арьяле и Надарадже исправлено.)
Две нижние диагональные записи информационной матрицы Фишера относительно параметра a (минимум диапазона распределения): , а по параметру c (максимум диапазона распределения): определены только для показателей α > 2 и β > 2 соответственно. Компонент информационной матрицы Фишера для минимума a приближается к бесконечности для показателя α, приближающегося к 2 сверху, и компонента информационной матрицы Фишера для максимума c стремится к бесконечности для показателя β, приближающегося к 2 сверху.
Информационная матрица Фишера для случая четырех параметров не зависит от отдельных значений минимума a и максимума c , а только от общего диапазона ( c − a ). Более того, компоненты информационной матрицы Фишера, которые зависят от диапазона ( c − a ), зависят только через свою обратную величину (или квадрат обратной), так что информация Фишера уменьшается с увеличением диапазона ( c − a ).
На прилагаемых изображениях показаны информационные компоненты Fisher. и . Изображения для информационных компонентов Fisher и показаны в § Геометрическая дисперсия . Все эти информационные компоненты Фишера имеют вид бассейна, «стенки» которого расположены при низких значениях параметров.
Следующие компоненты информации Фишера с четырьмя параметрами бета-распределения могут быть выражены через два параметра: X ~ Beta(α, β) ожидания преобразованного отношения ((1 − X )/ X ) и его зеркального отображения. ( X /(1 − X )), масштабируемый по диапазону ( c − a ), что может быть полезно для интерпретации:
Это также ожидаемые значения «обратного бета-распределения» или простого бета-распределения (также известного как бета-распределение второго рода или тип VI Пирсона ). [1] и его зеркальное изображение, масштабированное по диапазону ( c − a ).
Кроме того, следующие компоненты информации Фишера могут быть выражены через гармонические (1/X) дисперсии или дисперсии, основанные на соотношении преобразованных переменных ((1-X)/X) следующим образом:
Эти ожидания см. в разделе «Моменты линейно преобразованных, произведенных и инвертированных случайных величин».
Определитель информационной матрицы Фишера представляет интерес (например, для расчета априорной вероятности Джеффриса). Из выражений для отдельных компонент следует, что определитель (симметричной) информационной матрицы Фишера для бета-распределения с четырьмя параметрами равен:
Используя критерий Сильвестра (проверяя, все ли диагональные элементы положительны), и поскольку диагональные компоненты и имеют особенности при α=2 и β=2, то информационная матрица Фишера для четырехпараметрического случая положительно определена при α>2 и β>2. Поскольку при α > 2 и β > 2 бета-распределение имеет (симметричную или несимметричную) колоколообразную форму, отсюда следует, что информационная матрица Фишера положительно определена только для колоколообразных (симметричных или несимметричных) бета-распределений с точками перегиба, расположенными по обе стороны режима. Таким образом, важные хорошо известные распределения, принадлежащие к семейству бета-распределений с четырьмя параметрами, такие как параболическое распределение (Бета (2,2,a,c)) и равномерное распределение (Бета (1,1,a,c)) имеют Фишера информационные компоненты ( ), которые расширяются (стремятся к бесконечности) в случае с четырьмя параметрами (хотя все их информационные компоненты Фишера определены для случая с двумя параметрами). Четырехпараметрическое полукруговое распределение Вигнера (Beta(3/2,3/2, a , c )) и арксинусное распределение (Beta(1/2,1/2, a , c )) имеют отрицательные информационные детерминанты Фишера для четырех -параметрический случай.
Байесовский вывод [ править ]

Использование бета-распределений в байесовском выводе связано с тем, что они предоставляют семейство сопряженных априорных распределений вероятностей для биномиальных (включая Бернулли ) и геометрических распределений . Область бета-распределения можно рассматривать как вероятность, и фактически бета-распределение часто используется для описания распределения значения вероятности p : [23]
Примерами бета-распределений, используемых в качестве априорных вероятностей для представления незнания априорных значений параметров в байесовском выводе, являются Бета (1,1), Бета (0,0) и Бета (1/2,1/2).
Правило наследования [ править ]
Классическим применением бета-распределения является правило преемственности , введенное в 18 веке Пьером-Симоном Лапласом. [54] в ходе лечения проблемы восхода солнца . Он утверждает, что при условии s успехов в n условно независимых испытаниях Бернулли с вероятностью p оценка ожидаемого значения в следующем испытании равна . Эта оценка представляет собой ожидаемое значение апостериорного распределения по p, а именно Beta( s +1, n − s +1), которое определяется правилом Байеса , если предположить равномерную априорную вероятность по p (т. е. Beta(1, 1)) а затем замечает, что p обеспечил s успехов в n испытаниях. Правило преемственности Лапласа подверглось критике со стороны видных ученых. Р. Т. Кокс описал применение Лапласом правила последовательности к проблеме восхода солнца ( [55] п. 89) как «пародия на правильное использование принципа». Кейнс замечает ( [56] Гл.XXX, с. 382) «действительно, это настолько глупая теорема, что принимать ее в расчет постыдно». Карл Пирсон [57] показал, что вероятность того, что следующие ( n + 1) испытания будут успешными после n успехов в n испытаниях, составляет только 50%, что было сочтено такими учеными, как Джеффрис, слишком низким и неприемлемым как представление научного процесса экспериментирования. проверить предложенный научный закон. Как отметил Джеффрис ( [58] п. 128) (с указанием CD Broad [59] ) Правило преемственности Лапласа устанавливает высокую вероятность успеха ((n+1)/(n+2)) в следующем испытании, но лишь умеренную вероятность (50%) того, что следующая выборка (n+1), сопоставимая по размеру, будет столь же успешным. Как отметил Перкс, [60] «Само правило последовательности трудно принять. Оно присваивает вероятность следующему испытанию, что подразумевает предположение, что фактический наблюдаемый период является средним и что мы всегда находимся в конце среднего цикла. Было бы, можно было бы Думаю, было бы разумнее предположить, что мы находимся в середине среднего периода. Очевидно, что для обеих вероятностей необходимо более высокое значение, если они хотят согласовываться с разумным предположением». Эти проблемы с правилом преемственности Лапласа побудили Холдейна, Перкса, Джеффриса и других искать другие формы априорной вероятности (см. следующий § Байесовский вывод ). По словам Джейнса, [51] Основная проблема с правилом преемственности заключается в том, что оно недействительно, когда s=0 или s=n (см. правило преемственности для анализа его действительности).
Априорная вероятность Байеса – Лапласа (Бета (1,1)) [ править ]
Бета-распределение достигает максимальной дифференциальной энтропии для Beta(1,1): однородной плотности вероятности, для которой все значения в области распределения имеют одинаковую плотность. Это равномерное распределение Beta(1,1) было предложено («с большим сомнением») Томасом Байесом . [61] в качестве априорного распределения вероятностей, чтобы выразить незнание правильного априорного распределения. Это предварительное распределение было принято (видимо, из его сочинений, без особых сомнений). [54] ) Пьера-Симона Лапласа , и поэтому оно было также известно как «правило Байеса-Лапласа» или «правило Лапласа» « обратной вероятности » в публикациях первой половины 20-го века. В конце 19-го века и в начале 20-го века ученые поняли, что предположение о равномерной «равной» плотности вероятности зависит от реальных функций (например, от того, является ли линейная или логарифмическая шкала наиболее подходящей) и используемых параметризаций. . поведение вблизи концов распределений с конечным носителем (например, вблизи x = 0, для распределения с начальным носителем при x В частности, особого внимания требовало = 0). Кейнс ( [56] Гл.XXX, с. 381) раскритиковал использование байесовской равномерной априорной вероятности (Бета(1,1)), согласно которой все значения от нуля до единицы равновероятны, следующим образом: «Таким образом, опыт, если он что-то и показывает, показывает, что существует очень выраженная кластеризация статистических отношений в окрестностях нуля и единицы, для положительных теорий и для корреляций между положительными качествами в окрестности нуля, и для отрицательных теорий и для корреляций между отрицательными качествами в окрестности единицы».
Априорная вероятность Холдейна (Бета(0,0)) [ править ]

Распределение Бета(0,0) было предложено Дж.Б.С. Холдейном . [62] который предположил, что априорная вероятность, представляющая полную неопределенность, должна быть пропорциональна p −1 (1- п ) −1 . Функция р −1 (1- п ) −1 можно рассматривать как предел числителя бета-распределения, поскольку оба параметра формы стремятся к нулю: α, β → 0. Бета-функция (в знаменателе бета-распределения) приближается к бесконечности, для обоих параметров, стремящихся к нулю, α, β → 0. Следовательно, p −1 (1- п ) −1 разделенное на бета-функцию, приближается к двухточечному распределению Бернулли с равной вероятностью 1/2 на каждом конце, в точках 0 и 1, и ничего между ними, поскольку α, β → 0. Подбрасывание монеты: одна грань монеты в 0, а другая грань в 1. Априорное распределение вероятностей Холдейна Beta(0,0) является « неправильным априорным », поскольку его интегрирование (от 0 до 1) не может строго сходиться к 1 из-за особенностей на каждом конце. Однако это не проблема для вычисления апостериорных вероятностей, если только размер выборки не очень мал. Кроме того, Зельнер [63] указывает, что в шкале логарифмических шансов ( логит -преобразование ln( p /1 − p )) априор Холдейна является равномерно плоским приором. Тот факт, что равномерная априорная вероятность для логит -преобразованной переменной ln( p /1 − p ) (с областью определения (−∞, ∞)) эквивалентна априорной вероятности Холдейна в области [0, 1], был указан Гарольдом Джеффрисом. в первом издании (1939 г.) его книги «Теория вероятностей» ( [58] п. 123). Джеффрис пишет: «Конечно, если мы доведем правило Байеса-Лапласа до крайности, мы придем к результатам, которые не соответствуют чьему-либо образу мышления. Правило (Холдейна) d x /( x (1 − x )) тоже подходит. Совсем наоборот. Это привело бы к выводу, что если выборка относится к одному типу по какому-то свойству, существует вероятность 1, что вся совокупность принадлежит к этому типу». Тот факт, что «равномерность» зависит от параметризации, побудил Джеффриса искать форму априора, которая была бы инвариантной при различных параметризациях.
Априорная вероятность Джеффриса (Бета (1/2,1/2) для распределения Бернулли или для распределения биномиального )




Гарольд Джеффрис [58] [64] предложил использовать неинформативную априорную вероятностную меру, которая должна быть инвариантной при перепараметризации : пропорционально квадратному корню из определителя матрицы Фишера информационной . Для распределения Бернулли это можно показать следующим образом: для монеты, которая является «орлом» с вероятностью p ∈ [0, 1] и «решкой» с вероятностью 1 − p , для заданного (H,T) ∈ { (0,1), (1,0)} вероятность равна p ЧАС (1 - п ) Т . Поскольку T = 1 − H , распределение Бернулли равно p ЧАС (1 - п ) 1 - Ч . Учитывая p как единственный параметр, отсюда следует, что логарифмическое правдоподобие для распределения Бернулли равно
Информационная матрица Фишера имеет только один компонент (он является скаляром, поскольку имеется только один параметр: p ), поэтому:
Аналогично для биномиального распределения с n испытаниями Бернулли можно показать, что
Таким образом, для распределений Бернулли и биномиального распределения априор Джеффриса пропорционален , которое оказывается пропорциональным бета-распределению с доменной переменной x = p и параметрами формы α = β = 1/2, арксинусному распределению :
В следующем разделе будет показано, что константа нормализации априорного значения Джеффриса не имеет значения для конечного результата, поскольку константа нормализации сокращается в теореме Байеса для апостериорной вероятности. Следовательно, бета(1/2,1/2) используется в качестве априора Джеффриса как для распределения Бернулли, так и для биномиального распределения. Как показано в следующем разделе, при использовании этого выражения в качестве априорной вероятности, умноженной на правдоподобие в теореме Байеса , апостериорная вероятность оказывается бета-распределением. Однако важно понимать, что априор Джеффриса пропорционален для распределения Бернулли и биномиального распределения, но не для бета-распределения. Приоритет Джеффриса для бета-распределения определяется определителем информации Фишера для бета-распределения, который, как показано в § информационной матрице Фишера , является функцией тригамма-функции ψ 1 параметров формы α и β следующим образом:
Как обсуждалось ранее, априор Джеффриса для распределений Бернулли и биномиального распределения пропорционален арксинусному распределению Beta(1/2,1/2), одномерной кривой , которая выглядит как бассейн в зависимости от параметра p распределения Бернулли и биномиальные распределения. Стенки бассейна образуются за счет приближения p к особенностям на концах p → 0 и p → 1, где Beta(1/2,1/2) стремится к бесконечности. Предпосылка Джеффриса для бета-распределения представляет собой двумерную поверхность (встроенную в трехмерное пространство), которая выглядит как бассейн, только две стенки которого сходятся в углу α = β = 0 (и две другие стенки отсутствуют), как функция параметров формы α и β бета-распределения. Две прилегающие стенки этой двумерной поверхности образованы параметрами формы α и β, приближающимися к особенностям (тригамма-функции) при α, β → 0. Она не имеет стенок при α, β → ∞, поскольку в этом случае определитель информационной матрицы Фишера для бета-распределения приближается к нулю.
В следующем разделе будет показано, что априорная вероятность Джеффриса приводит к апостериорным вероятностям (при умножении на биномиальную функцию правдоподобия), которые являются промежуточными между результатами апостериорной вероятности априорных вероятностей Холдейна и Байеса.
Априорное значение Джеффриса может быть трудно получить аналитически, а в некоторых случаях оно просто не существует (даже для простых функций распределения, таких как асимметричное треугольное распределение ). Бергер, Бернардо и Сан, в статье 2009 г. [65] определил эталонное априорное распределение вероятностей, которое (в отличие от априорного распределения Джеффриса) существует для асимметричного треугольного распределения . Они не могут получить выражение в замкнутой форме для своего эталонного априорного значения, но численные расчеты показывают, что оно почти идеально соответствует (правильному) априорному значению.
где θ — переменная вершины для асимметричного треугольного распределения с поддержкой [0, 1] (соответствует следующим значениям параметров в статье Википедии о треугольном распределении : вершина c = θ , левый конец a = 0 и правый конец b = 1). ). Бергер и др. также приведите эвристический аргумент в пользу того, что Beta(1/2,1/2) действительно может быть точной априорной ссылкой Бергера – Бернардо – Сана для асимметричного треугольного распределения. Таким образом, Beta(1/2,1/2) не только является априорным значением Джеффриса для распределений Бернулли и биномиального распределения, но также, по-видимому, является априорным эталоном Бергера–Бернардо–Сан для асимметричного треугольного распределения (для которого априорное значение Джеффриса не существует), распределение, используемое в управлении проектами и анализе PERT для описания стоимости и продолжительности задач проекта.
Кларк и Бэррон [66] Шеннона докажите, что среди непрерывных положительных априоров априор Джеффриса (если он существует) асимптотически максимизирует взаимную информацию между выборкой размера n и параметром, и, следовательно, априор Джеффриса является наиболее неинформативным априором (измеряя информацию как информацию Шеннона). Доказательство основано на исследовании расхождения Кульбака–Лейблера между функциями плотности вероятности для iid случайных величин.
Влияние различных вариантов априорной вероятности на апостериорное бета - распределение
Если выборки взяты из совокупности случайной величины X, что приводит к s успехам и f неудачам в n испытаниях Бернулли n = s + f , то функция правдоподобия для параметров s и f при условии x = p (обозначение x = p в выражения ниже подчеркнут, что область x обозначает значение параметра p в биномиальном распределении), представляет собой следующее биномиальное распределение :
Если убеждения об априорной информации о вероятности достаточно хорошо аппроксимируются бета-распределением с параметрами α Prior и β Prior, тогда:
Согласно теореме Байеса для непрерывного пространства событий, апостериорная плотность вероятности определяется произведением априорной вероятности и функции правдоподобия (с учетом доказательств s и f = n - s ), нормализованной так, что площадь под кривой равна один, а именно:
коэффициент Биномиальный
появляется как в числителе, так и в знаменателе апостериорной вероятности, и не зависит от переменной интегрирования x , следовательно, сокращается и не имеет отношения к конечному результату. Аналогично, нормирующий коэффициент для априорной вероятности, бета-функция B(αPrior,βPrior), сокращается и не имеет значения для конечного результата. Тот же результат апостериорной вероятности можно получить, если использовать ненормализованное априорное значение.
потому что все нормализующие факторы компенсируются. Таким образом, некоторые авторы (включая самого Джеффриса) используют ненормализованную априорную формулу, поскольку константа нормализации уравновешивается. Числитель апостериорной вероятности в конечном итоге оказывается просто (ненормализованным) произведением априорной вероятности и функции правдоподобия, а знаменатель — ее интегралом от нуля до единицы. Бета-функция в знаменателе B( s + α Prior, n - s + β Prior) появляется как константа нормализации, гарантирующая, что общая апостериорная вероятность интегрируется до единицы.
Отношение s / n числа успехов к общему числу испытаний является достаточной статистикой в биномиальном случае, что актуально для следующих результатов.
Для априорной вероятности Байеса (Бета (1,1)), апостериорная вероятность равна:
Для априорной вероятности Джеффриса (Бета (1/2,1/2)), апостериорная вероятность равна:
а для априорной вероятности Холдейна (Бета (0,0)) апостериорная вероятность равна:
Из приведенных выше выражений следует, что для s / n = 1/2) все три вышеуказанные априорные вероятности приводят к идентичному расположению апостериорной вероятности, среднее = мода = 1/2. Для s / n < 1/2 среднее значение апостериорных вероятностей с использованием следующих априорных значений таково: среднее значение для априора Байеса > среднее значение для априора Джеффриса > среднее значение для априора Холдейна. Для s / n > 1/2 порядок этих неравенств меняется на обратный, так что априорная вероятность Холдейна приводит к наибольшему апостериорному среднему. Априорная вероятность Холдейна s Бета(0,0) приводит к апостериорной плотности вероятности со средним значением (ожидаемое значение вероятности успеха в «следующем» испытании), идентичным отношению / n числа успехов к общему числу испытаний. Таким образом, априорный результат Холдейна дает апостериорную вероятность с ожидаемым значением в следующем испытании, равным максимальному правдоподобию. Априорная вероятность Байеса идентичной Beta(1,1) приводит к апостериорной плотности вероятности с модой, отношению s / n (максимальное правдоподобие).
В случае, если 100% испытаний были успешными s = n , априорная вероятность Байеса Beta(1,1) приводит к апостериорному ожидаемому значению, равному правилу последовательности ( n + 1)/( n + 2), в то время как априорная бета-версия Холдейна (0,0) дает апостериорное ожидаемое значение, равное 1 (абсолютная уверенность в успехе в следующем испытании). Априорная вероятность Джеффри приводит к апостериорному ожидаемому значению, равному ( n + 1/2)/( n + 1). льготы [60] (стр. 303) отмечает: «Это обеспечивает новое правило последовательности и выражает «разумную» позицию, которую следует занять, а именно, что после непрерывной серии из n успехов мы предполагаем вероятность следующего испытания, эквивалентную предположению, что мы находимся примерно на середине среднего пробега, т.е. мы ожидаем неудачу один раз в (2 n + 2) испытаниях. Правило Байеса-Лапласа подразумевает, что мы находимся примерно в конце среднего пробега или что мы ожидаем неудачу. один раз в ( n + 2) испытаниях. Сравнение явно свидетельствует в пользу нового результата (того, что теперь называется априорным Джеффрисом) с точки зрения «разумности».
И наоборот, в случае, если 100% испытаний закончились неудачей ( s = 0), априорная вероятность Байеса Beta(1,1) приводит к апостериорному ожидаемому значению успеха в следующем испытании, равному 1/( n + 2), в то время как априорная бета-версия Холдейна (0,0) приводит к апостериорному ожидаемому значению успеха в следующем испытании, равному 0 (абсолютная уверенность в неудаче в следующем испытании). Априорная вероятность Джеффриса приводит к апостериорному ожидаемому значению успеха в следующем испытании, равному (1/2)/( n + 1), что Перкс [60] (стр. 303) указывает: «это гораздо более отдаленный результат, чем результат Байеса – Лапласа 1/( n + 2)».
Джейнс [51] вопросы (для равномерного априора Beta(1,1)) использование этих формул для случаев s = 0 или s = n , поскольку интегралы не сходятся (Beta(1,1) является несобственным априором для s = 0 или s = п ). На практике условия 0<s<n, необходимые для существования режима между обоими концами для априора Байеса, обычно выполняются, и поэтому априор Байеса (пока 0 < s < n ) приводит к апостериорной моде, расположенной между обоими концы домена.
Как отмечалось в разделе о правиле последовательности, К. Пирсон показал, что после n успехов в n испытаниях апостериорная вероятность (основанная на распределении Байеса-бета(1,1) в качестве априорной вероятности) того, что следующее ( n + 1) все испытания будут успешными, ровно 1/2, независимо от значения n . На основе бета-распределения Холдейна (0,0) в качестве априорной вероятности эта апостериорная вероятность равна 1 (абсолютная уверенность в том, что после n успехов в n испытаниях все следующие ( n + 1) испытаний будут успешными). льготы [60] (стр. 303) показывает, что для того, что сейчас известно как априор Джеффриса, эта вероятность равна (( n + 1/2)/( n + 1))(( n + 3/2)/( n + 2) )...(2 n + 1/2)/(2 n + 1), что для n = 1, 2, 3 дает 15/24, 315/480, 9009/13440; быстро приближается к предельному значению поскольку n стремится к бесконечности. Перкс отмечает, что то, что сейчас известно как априор Джеффриса: «явно более «разумно», чем результат Байеса-Лапласа или результат альтернативного правила (Холдейна), отвергнутого Джеффрисом, который дает уверенность в качестве вероятности. Он явно обеспечивает гораздо лучшее соответствие процессу индукции. Вопрос о том, является ли он «абсолютно» разумным для этой цели, т. е. достаточно ли он велик, без абсурдности достижения единства, — это вопрос, который должны решить другие. результат зависит от предположения о полном безразличии и отсутствии знаний до выборочного эксперимента».
Ниже приведены дисперсии апостериорного распределения, полученные с помощью этих трех априорных распределений вероятностей:
для априорной вероятности Байеса (Бета (1,1)), апостериорная дисперсия равна:
для априорной вероятности Джеффриса (Бета (1/2,1/2)), апостериорная дисперсия равна:
а для априорной вероятности Холдейна (Бета (0,0)) апостериорная дисперсия равна:
Итак, как заметил Сильви, [49] для больших n дисперсия мала и, следовательно, апостериорное распределение сильно сконцентрировано, тогда как предполагаемое априорное распределение было очень размытым. Это соответствует тому, на что можно было бы надеяться, поскольку расплывчатое априорное знание преобразуется (посредством теоремы Байеса) в более точное апостериорное знание посредством информативного эксперимента. Для малых n априорное значение бета-версии Холдейна (0,0) приводит к наибольшей апостериорной дисперсии, тогда как априорное значение бета-версии Байеса (1,1) приводит к более концентрированному апостериорному отклонению. Предыдущая бета-версия Джеффри (1/2,1/2) приводит к апостериорному отклонению между двумя другими. По мере увеличения n дисперсия быстро уменьшается, так что апостериорная дисперсия для всех трех априорных значений сходится примерно к одному и тому же значению (приближаясь к нулевой дисперсии при n → ∞). Вспоминая предыдущий результат, что априорная вероятность Холдейна Бета(0,0) приводит к апостериорной плотности вероятности со средним (ожидаемым значением вероятности успеха в «следующем» испытании), идентичным отношению s/n числа успехов к общему числу испытаний, из приведенного выше выражения следует, что и Априорная бета-версия Холдейна (0,0) дает апостериорный результат с дисперсией , идентичной дисперсии, выраженной через макс. оценка правдоподобия s/n и размер выборки (в § Дисперсия ):
со средним значением µ = s / n и размером выборки ν = n .
В байесовском выводе использование априорного распределения Бета ( α Приор, β Приор) перед биномиальным распределением эквивалентно добавлению ( α Приор - 1) псевдонаблюдений «успеха» и ( β Приор - 1) псевдонаблюдений «успеха». неудач» до фактического количества наблюдаемых успехов и неудач, а затем оцениваю параметр p биномиального распределения по доле успехов как в реальных, так и в псевдонаблюдениях. Равномерная априорная бета(1,1) не добавляет (или вычитает) никаких псевдонаблюдений, поскольку для Beta(1,1) следует, что ( α Prior − 1) = 0 и ( β Prior − 1) = 0. Априорное бета-тестирование Холдейна (0,0) вычитает одно псевдонаблюдение из каждого, а априорное бета-наблюдение Джеффри (1/2,1/2) вычитает 1/2 псевдонаблюдения успеха и такое же количество неудач. Это вычитание приводит к сглаживанию апостериорного распределения. Если доля успешных результатов не составляет 50% ( s / n ≠ 1/2), значения α Prior и β Prior меньше 1 (и, следовательно, отрицательные ( α Prior − 1) и ( β Prior − 1)) благоприятствуют разреженности, т.е. распределения, где параметр p ближе к 0 или 1. По сути, значения α Prior и β Prior от 0 до 1 при совместной работе действуют как параметр концентрации .
Прилагаемые графики показывают апостериорные функции плотности вероятности для размеров выборки n ∈ {3,10,50}, успехов s ∈ { n /2, n /4} и Beta( α Prior, β Prior) ∈ {Beta(0,0 ),Бета(1/2,1/2),Бета(1,1)}. Также показаны случаи для n = {4,12,40}, успеха s = { n /4} и Beta( α Prior, β Prior) ∈ {Beta(0,0), Beta(1/2,1/ 2),Бета(1,1)}. На первом графике показаны симметричные случаи для успехов s ∈ {n/2} со средним значением = mode = 1/2, а на втором графике показаны асимметричные случаи s ∈ { n /4}. Изображения показывают, что разница между априорными данными для апостериорной группы незначительна при размере выборки 50 (характеризуется более выраженным пиком вблизи p = 1/2). Значительные различия появляются для очень маленьких размеров выборки (в частности, для более плоского распределения для вырожденного случая размера выборки = 3). Таким образом, асимметричные случаи с успехами s = { n /4} демонстрируют больший эффект от выбора априора при небольшом размере выборки, чем симметричные случаи. Для симметричных распределений априорное бета-распределение Байеса (1,1) приводит к наиболее «остроконечным» и самым высоким апостериорным распределениям, а априорное бета-распределение Холдейна (0,0) приводит к самому плоскому и самому низкому пиковому распределению. Предыдущая бета-версия Джеффриса (1/2,1/2) находится между ними. Для почти симметричных, не слишком асимметричных распределений эффект априорных значений аналогичен. Для очень маленького размера выборки (в данном случае для размера выборки 3) и неравномерного распределения (в этом примере для s ∈ { n /4}) априор Холдейна может привести к обратному J-образному распределению с особенностью на левом конце. Однако это происходит только в вырожденных случаях (в этом примере n = 3 и, следовательно, s = 3/4 <1, вырожденное значение, поскольку s должно быть больше единицы, чтобы апостериорная часть Холдейна до того имела моду, расположенную между концы, и поскольку s = 3/4 не является целым числом, следовательно, оно нарушает первоначальное предположение о биномиальном распределении вероятности) и не является проблемой в общих случаях разумного размера выборки (таких, что условие 1 < s < n − 1, необходимое для существования режима между обоими концами, выполняется).
В главе 12 (стр. 385) своей книги Джейнс [51] утверждает, что априорная бета-версия Холдейна (0,0) описывает априорное состояние знания при полном незнании , когда мы даже не уверены, физически возможно, что эксперимент приведет к успеху или неудаче, в то время как байесовский (равномерный) предыдущая бета(1,1) применяется, если известно, что возможны оба двоичных результата . Джейнс утверждает: « интерпретируйте априорное правило Байеса-Лапласа (Бета(1,1)) как описывающее не состояние полного невежества , а состояние знания, в котором мы наблюдали один успех и одну неудачу... однажды мы увидели хотя бы один успех и одна неудача, то мы знаем, что эксперимент является истинно бинарным в смысле физической возможности». Джейнс [51] конкретно не обсуждается предыдущая бета-версия Джеффриса (1/2,1/2) (обсуждение Джейном «предшествующей бета-версии Джеффриса» на стр. 181, 423 и в главе 12 книги Джейнса). [51] вместо этого относится к неправильному, ненормализованному предшествующему «1/ p dp », введенному Джеффрисом в издании его книги 1939 года, [58] за семь лет до этого он представил то, что сейчас известно как априорный инвариант Джеффриса: квадратный корень из определителя информационной матрицы Фишера. «1/p» — это априорный инвариант Джеффриса (1946) для экспоненциального распределения , а не для распределения Бернулли или биномиального распределения ). Однако из приведенного выше обсуждения следует, что априорная бета-версия Джеффриса (1/2,1/2) представляет собой состояние знаний, промежуточное между бета-версией Холдейна (0,0) и априорной бета-версией Байеса (1,1).
Точно так же Карл Пирсон в своей книге 1892 года «Грамматика науки» [67] [68] (стр. 144 издания 1900 года) утверждал, что единый априор Байеса (Бета (1,1) не является априором полного незнания и что его следует использовать, когда априорная информация оправдывает «равномерное распределение нашего незнания»». К. Пирсон писал: «Однако единственное предположение, которое мы, по-видимому, сделали, состоит в том, что, ничего не зная о природе, следует считать рутину и аномию (от греческого ανομία, а именно: а- «без» и nomos «закон»). такое же вероятное явление. Но даже это предположение не имело на самом деле оснований, поскольку оно предполагает знание природы, которым мы не обладаем. Мы используем наш опыт строения и действия монет в целом, чтобы утверждать, что орел и решка. одинаково вероятны, но мы не имеем права утверждать до опыта, что, поскольку мы ничего не знаем о природе, рутина и нарушение одинаково вероятны, по нашему незнанию, мы должны до опыта считать, что природа может состоять из всякой рутины, из всех аномий (безнормальности). ), или смесь того и другого в любой пропорции, и что все это одинаково вероятно. Какая из этих конституций после опыта является наиболее вероятной, очевидно, зависит от того, каким был этот опыт».
Если имеется достаточно данных выборки , а апостериорная мода вероятности не расположена на одном из крайних значений области ( x = 0 или x = 1), три априора Байеса (Бета(1,1)), Джеффриса (Бета (1/2,1/2)) и Холдейна (Бета(0,0)) должны давать аналогичные апостериорные плотности вероятности . В противном случае, как отмечают Гельман и др. [69] (стр. 65) отмечают: «если доступно так мало данных, что выбор неинформативного априорного распределения имеет значение, следует поместить соответствующую информацию в априорное распределение», или, как Бергер [4] (стр. 125) указывает, что «когда разные разумные априорные положения дают существенно разные ответы, может ли быть правильным утверждать, что существует единственный ответ? Не лучше ли было бы признать, что существует научная неопределенность, при которой вывод зависит от предшествующих убеждений?» ?».
Возникновение и применение [ править ]
Статистика заказов [ править ]
Бета-распределение имеет важное применение в теории статистики порядка . Основной результат состоит в том, что распределение k -й наименьшей выборки размера n из непрерывного равномерного распределения имеет бета-распределение. [38] Этот результат суммируется как:
Исходя из этого и применения теории, связанной с преобразованием интеграла вероятности распределение любой статистики отдельного порядка из любого непрерывного распределения . , можно получить [38]
Субъективная логика [ править ]
В стандартной логике предложения считаются либо истинными, либо ложными. Напротив, субъективная логика предполагает, что люди не могут с абсолютной уверенностью определить, является ли утверждение о реальном мире абсолютно истинным или ложным. В субъективной логике оценки апостериорные вероятности бинарных событий могут быть представлены бета-распределениями. [70]
Вейвлет-анализ [ править ]
Вейвлет , которая начинается — это волнообразное колебание с амплитудой с нуля, увеличивается, а затем снова уменьшается до нуля. Обычно его можно представить как «краткое колебание», которое быстро затухает. Вейвлеты можно использовать для извлечения информации из самых разных типов данных, включая, помимо прочего, аудиосигналы и изображения. Таким образом, вейвлеты специально создаются так, чтобы иметь определенные свойства, которые делают их полезными для обработки сигналов . Вейвлеты локализованы как по времени, так и по частоте, тогда как стандартное преобразование Фурье локализовано только по частоте. Следовательно, стандартные преобразования Фурье применимы только к стационарным процессам , а вейвлеты применимы к нестационарным процессам . Непрерывные вейвлеты могут быть построены на основе бета-распределения. Бета-вейвлеты [71] можно рассматривать как мягкую разновидность вейвлетов Хаара , форма которых точно настраивается двумя параметрами формы α и β.
генетика Популяционная
Модель Болдинга-Николса представляет собой двухпараметрическую параметризацию бета-распределения, используемую в популяционной генетике . [72] Это статистическое описание частот аллелей в компонентах подразделенной популяции:
где и ; здесь F — генетическое расстояние (Райта) между двумя популяциями.
проектами: моделирование стоимости задач и расписания Управление
Бета-распределение можно использовать для моделирования событий, которые должны происходить в интервале, определяемом минимальным и максимальным значением. По этой причине бета-распределение — наряду с треугольным распределением — широко используется в PERT , методе критического пути (CPM), совместном моделировании графика затрат (JCSM) и других системах управления/контроля проектов для описания времени завершения и стоимости. задачи. широко используются сокращенные вычисления : В управлении проектами для оценки среднего и стандартного отклонения бета-распределения [37]
где a – минимум, c – максимум, b – наиболее вероятное значение ( режим для α > 1 и β > 1).
Приведенная выше оценка среднего известна как PERT трехточечная оценка и точна для любого из следующих значений β (для произвольного α в этих диапазонах):
- β = α > 1 (симметричный случай) со стандартным отклонением , асимметрия = 0 и избыточный эксцесс =
или
- β = 6 − α для 5 > α > 1 (асимметричный случай) со стандартным отклонением
асимметрия , и избыточный эксцесс
Приведенная выше оценка стандартного отклонения σ ( X ) = ( c − a )/6 точна для любого из следующих значений α и β :
- α = β = 4 (симметричный) с асимметрией = 0 и избыточным эксцессом = −6/11.
- β = 6 − α и (правосторонний, положительный перекос) с асимметрией , и избыточный эксцесс = 0
- β = 6 − α и (левосторонний, отрицательный перекос) с асимметрией , и избыточный эксцесс = 0
В противном случае это могут быть плохие аппроксимации для бета-распределений с другими значениями α и β, демонстрирующие средние ошибки 40% в среднем и 549% в дисперсии. [73] [74] [75]
Генерация случайной переменной [ править ]
Если X и Y независимы, при этом и затем
Таким образом, один из алгоритмов генерации бета-вариантов состоит в том, чтобы сгенерировать , где X — гамма-переменная с параметрами (α, 1), а Y — независимая гамма-переменная с параметрами (β, 1). [76] На самом деле здесь и независимы, и . Если и не зависит от и , затем и не зависит от . Это показывает, что произведение независимых и случайные величины – это случайная величина.
Кроме того, статистика k -го порядка из n равномерно распределенных переменных равна , поэтому альтернативой, если α и β являются маленькими целыми числами, является создание равномерных переменных α + β − 1 и выбор α-й наименьшей. [38]
Другой способ создания бета-распределения — использование модели урны Полиа . Согласно этому методу, начинают с «урны» с α «черными» шарами и β «белыми» шарами и равномерно рисуют с заменой. В каждой попытке добавляется дополнительный шар в зависимости от цвета последнего выпавшего шара. Асимптотически пропорция черных и белых шаров будет распределяться в соответствии с бета-распределением, где каждое повторение эксперимента будет давать разное значение.
Также возможно использовать выборку обратного преобразования .
к бета - распределению Нормальное приближение
Бета-дистрибутив с α ~ β и α и β >> 1 примерно нормально со средним значением 1/2 и дисперсией 1/(4(2 α + 1)). Если α ≥ β, нормальное приближение можно улучшить, взяв кубический корень из логарифма обратной величины. [77]
История [ править ]
Томас Байес в посмертной статье [61] опубликованный в 1763 году Ричардом Прайсом , получил бета-распределение как плотность вероятности успеха в испытаниях Бернулли (см. § Приложения, Байесовский вывод ), но в статье не анализируется ни один из моментов бета-распределения и не обсуждаются какие-либо его характеристики.

Первое систематическое современное обсуждение бета-распределения принадлежит, вероятно, Карлу Пирсону . [78] [79] В бумагах Пирсона [20] [32] бета-распределение представлено как решение дифференциального уравнения: распределение Пирсона типа I , которому оно по сути идентично, за исключением произвольного сдвига и масштабирования (бета-распределение и распределение Пирсона типа I всегда можно выровнять путем правильного выбора параметров). Фактически, в нескольких английских книгах и журнальных статьях за несколько десятилетий до Второй мировой войны бета-распределение было принято называть распределением Пирсона типа I. Уильям П. Элдертон в своей монографии 1906 года «Частотные кривые и корреляция». [41] далее анализируется бета-распределение как распределение типа I Пирсона, включая полное обсуждение метода моментов для случая четырех параметров и диаграммы (то, что Элдертон называет) U-образными, J-образными, скрученными J-образными, «взведенными» -шляпной формы, горизонтальные и угловые прямолинейные корпуса. Элдертон писал: «Я главным образом в долгу перед профессором Пирсоном, но это такая задолженность, за которую невозможно выразить официальную благодарность». Элдертон в своей монографии 1906 года. [41] предоставляет впечатляющий объем информации о бета-распределении, включая уравнения происхождения распределения, выбранного в качестве моды, а также других распределений Пирсона: типов от I до VII. Элдертон также включил ряд приложений, в том числе одно приложение («II») по бета- и гамма-функциям. В более поздних изданиях Элдертон добавил уравнения происхождения распределения, выбранного в качестве среднего, и анализ распределений Пирсона с VIII по XII.
Как заметили Боумен и Шентон [43] «У Фишера и Пирсона были разногласия в подходе к оценке (параметров), в частности, в отношении моментов (метода Пирсона) и максимального правдоподобия (метода Фишера) в случае бета-распределения». Также, по мнению Боумана и Шентона, «случай, когда модель типа I (бета-распределение) оказалась в центре разногласий, был чистой случайностью. Трудно было бы найти более сложную модель с четырьмя параметрами». За длительным публичным конфликтом Фишера с Карлом Пирсоном можно следить в ряде статей в престижных журналах. Например, по поводу оценки четырех параметров бета-распределения и критики Фишером метода моментов Пирсона как произвольного см. статью Пирсона «Метод моментов и метод максимального правдоподобия». [44] (опубликовано через три года после его выхода на пенсию из Университетского колледжа в Лондоне, где его должность была разделена между Фишером и сыном Пирсона Эгоном), в которой Пирсон пишет: «Я читал (статью Кошая в Журнале Королевского статистического общества, 1933 г.), которая, насколько насколько мне известно, это единственный опубликованный в настоящее время случай применения метода профессора Фишера. К моему удивлению, этот метод основан на сначала вычислении констант частотной кривой с помощью метода моментов (Пирсона), а затем наложении на них с помощью метода моментов. то, что Фишер называет «методом максимального правдоподобия», является дальнейшим приближением для получения того, чего он придерживается, он, таким образом, получит «более эффективные значения» констант кривой».
Трактат Дэвида и Эдвардса по истории статистики [80] цитирует первую современную трактовку бета-распределения, сделанную в 1911 году: [81] используя обозначение бета, ставшее стандартным, благодаря Коррадо Джини , итальянскому статистику , демографу и социологу , разработавшему коэффициент Джини . Н.Л.Джонсон и С.Коц в своей обширной и очень информативной монографии. [82] о ведущих исторических деятелях в области статистических наук Коррадо Джини. [83] как «ранний байесианец... который занимался проблемой выявления параметров начального бета-распределения, выделяя методы, которые предвосхитили появление так называемого эмпирического байесовского подхода».
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л м н тот п д р с т в v В х и Джонсон, Норман Л.; Коц, Сэмюэл; Балакришнан, Н. (1995). «Глава 25: Бета-распределения». Непрерывные одномерные распределения Vol. 2 (2-е изд.). Уайли. ISBN 978-0-471-58494-0 .
- ↑ Перейти обратно: Перейти обратно: а б Роуз, Колин; Смит, Мюррей Д. (2002). Математическая статистика с помощью MATHEMATICA . Спрингер. ISBN 978-0387952345 .
- ↑ Перейти обратно: Перейти обратно: а б с Крушке, Джон К. (2011). Выполнение байесовского анализа данных: учебное пособие по R и BUGS . Академическая пресса / Эльзевир. п. 83. ИСБН 978-0123814852 .
- ↑ Перейти обратно: Перейти обратно: а б Бергер, Джеймс О. (2010). Статистическая теория принятия решений и байесовский анализ (2-е изд.). Спрингер. ISBN 978-1441930743 .
- ↑ Перейти обратно: Перейти обратно: а б с д Феллер, Уильям (1971). Введение в теорию вероятностей и ее приложения, Vol. 2 . Уайли. ISBN 978-0471257097 .
- ^ Крушке, Джон К. (2015). Выполнение байесовского анализа данных: руководство с R, JAGS и Stan . Академическая пресса / Эльзевир. ISBN 978-0-12-405888-0 .
- ↑ Перейти обратно: Перейти обратно: а б Уодсворт, Джордж П. и Джозеф Брайан (1960). Введение в теорию вероятности и случайных величин . МакГроу-Хилл.
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г Гупта, Арджун К., изд. (2004). Справочник по бета-дистрибутиву и его приложениям . ЦРК Пресс. ISBN 978-0824753962 .
- ↑ Перейти обратно: Перейти обратно: а б Керман, Джуни (2011). «Приближение в замкнутой форме для медианы бета-распределения». arXiv : 1111.0433 [ math.ST ].
- ^ Мостеллер, Фредерик и Джон Тьюки (1977). Анализ данных и регрессия: второй курс статистики . Паб Аддисон-Уэсли. компании Бибкод : 1977dars.book.....M . ISBN 978-0201048544 .
- ↑ Перейти обратно: Перейти обратно: а б Феллер, Уильям (1968). Введение в теорию вероятностей и ее приложения . Том. 1 (3-е изд.). ISBN 978-0471257080 .
- ^ Филип Дж. Флеминг и Джон Дж. Уоллес. Как не соврать со статистикой: как правильно обобщить результаты бенчмарков . Сообщения ACM, 29(3):218–221, март 1986 г.
- ^ «Электронный справочник NIST/SEMATECH по статистическим методам 1.3.6.6.17. Бета-распределение» . Национального института стандартов и технологий Лаборатория информационных технологий . Апрель 2012 года . Проверено 31 мая 2016 г.
- ^ Огуаманам, DCD; Мартин, HR; Хьюиссун, JP (1995). «О применении бета-распределения для анализа повреждений зубчатых передач». Прикладная акустика . 45 (3): 247–261. дои : 10.1016/0003-682X(95)00001-P .
- ^ Чжицян Лян; Цзяньмин Вэй; Цзюнь Чжао; Хайтао Лю; Баоцин Ли; Цзе Шен; Чунлей Чжэн (27 августа 2008 г.). «Статистическое значение куртозиса и его новое применение для идентификации людей по сейсмическим сигналам» . Датчики . 8 (8): 5106–5119. Бибкод : 2008Senso...8.5106L . дои : 10.3390/s8085106 . ПМЦ 3705491 . ПМИД 27873804 .
- ^ Кенни, Дж. Ф. и Э. С. Кикинг (1951). Математика статистики. Часть вторая, 2-е издание . Компания Д. Ван Ностранд, Inc.
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ↑ Перейти обратно: Перейти обратно: а б с д Абрамовиц, Милтон и Ирен А. Стегун (1965). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Дувр. ISBN 978-0-486-61272-0 .
- ^ Вайсштейн., Эрик В. «Куртосис» . MathWorld — веб-ресурс Wolfram . Проверено 13 августа 2012 г.
- ↑ Перейти обратно: Перейти обратно: а б Паник, Майкл Дж (2005). Расширенная статистика с элементарной точки зрения . Академическая пресса. ISBN 978-0120884940 .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж Пирсон, Карл (1916). «Математический вклад в теорию эволюции, XIX: Второе приложение к мемуарам о асимметрии» . Философские труды Королевского общества А. 216 (538–548): 429–457. Бибкод : 1916RSPTA.216..429P . дои : 10.1098/rsta.1916.0009 . JSTOR 91092 .
- ^ Градштейн Израиль Соломонович ; Рыжик Иосиф Моисеевич ; Героним Юрий Вениаминович ; Цейтлин Михаил Юльевич ; Джеффри, Алан (2015) [октябрь 2014 г.]. Цвиллингер, Дэниел; Молл, Виктор Гюго (ред.). Таблица интегралов, рядов и произведений . Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. ISBN 978-0-12-384933-5 . LCCN 2014010276 .
- ^ Биллингсли, Патрик (1995). «30». Вероятность и мера (3-е изд.). Уайли-Интерсайенс. ISBN 978-0-471-00710-4 .
- ↑ Перейти обратно: Перейти обратно: а б Маккей, Дэвид (2003). Теория информации, логический вывод и алгоритмы обучения . Издательство Кембриджского университета; Первое издание. Бибкод : 2003itil.book.....М . ISBN 978-0521642989 .
- ↑ Перейти обратно: Перейти обратно: а б Джонсон, Нидерланды (1949). «Системы частотных кривых, порожденные методами трансляции» (PDF) . Биометрика . 36 (1–2): 149–176. дои : 10.1093/biomet/36.1-2.149 . hdl : 10338.dmlcz/135506 . ПМИД 18132090 .
- ^ Вердуго Лазо, ACG; Рэти, ПН (1978). «Об энтропии непрерывных вероятностных распределений». IEEE Транс. Инф. Теория . 24 (1): 120–122. дои : 10.1109/TIT.1978.1055832 .
- ^ Шеннон, Клод Э. (1948). «Математическая теория связи». Технический журнал Bell System . 27 (4): 623–656. дои : 10.1002/j.1538-7305.1948.tb01338.x .
- ↑ Перейти обратно: Перейти обратно: а б с Обложка, Томас М. и Джой А. Томас (2006). Элементы теории информации, 2-е издание (Серия Wiley по телекоммуникациям и обработке сигналов) . Уайли-Интерсайенс; 2 издание. ISBN 978-0471241959 .
- ^ Планкетт, Ким и Джеффри Элман (1997). Упражнения по переосмыслению врожденности: Справочник по коннекционистскому моделированию (моделирование нейронных сетей и коннекционизм) . Книга Брэдфорда. п. 166. ИСБН 978-0262661058 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Наллапати, Рамеш (2006). Сглаженное распределение Дирихле: понимание кросс-энтропийного ранжирования при поиске информации (Диссертация). Кафедра компьютерных наук Массачусетского университета в Амхерсте.
- ↑ Перейти обратно: Перейти обратно: а б Пирсон, Эгон С. (июль 1969 г.). «Некоторые исторические размышления прослеживаются в развитии использования частотных кривых» . Программа исследований статистического анализа THEMIS, технический отчет 38 . Управление военно-морских исследований, контракт №000014-68-А-0515 (проект №042–260).
- ^ Хан, Джеральд Дж.; Шапиро, С. (1994). Статистические модели в технике (Библиотека Wiley Classics) . Уайли-Интерсайенс. ISBN 978-0471040651 .
- ↑ Перейти обратно: Перейти обратно: а б Пирсон, Карл (1895). «Вклад в математическую теорию эволюции, II: Асимметрия в однородном материале» . Философские труды Королевского общества . 186 : 343–414. Бибкод : 1895RSPTA.186..343P . дои : 10.1098/rsta.1895.0010 . JSTOR 90649 .
- ^ Бьюкенен, К.; Роквей, Дж.; Штернберг, О.; Май, НН (май 2016 г.). «Суммально-разностное формирование диаграммы направленности для радиолокационных приложений с использованием случайных решеток с круговой конусностью» . Конференция IEEE по радиолокации 2016 (RadarConf) . стр. 1–5. дои : 10.1109/RADAR.2016.7485289 . ISBN 978-1-5090-0863-6 . S2CID 32525626 .
- ^ Бьюкенен, К.; Флорес, К.; Уиланд, С.; Дженсен, Дж.; Грейсон, Д.; Хафф, Г. (май 2017 г.). «Формирование луча для радиолокационных приложений с использованием случайных решеток с круговой конусностью». Конференция IEEE по радиолокации 2017 (RadarConf) . стр. 0112–0117. дои : 10.1109/RADAR.2017.7944181 . ISBN 978-1-4673-8823-8 . S2CID 38429370 .
- ^ Райан, Бьюкенен, Кристофер (29 мая 2014 г.). «Теория и приложения апериодических (случайных) фазированных решеток» .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Эррериас-Веласко, Хосе Мануэль и Эррериас-Плегесуэло, Рафаэль и Рене ван Дорп, Йохан. (2011). Возвращаясь к среднему значению PERT и дисперсии. Европейский журнал операционных исследований (210), с. 448–451.
- ↑ Перейти обратно: Перейти обратно: а б Малькольм, генеральный директор; Роузбум, Дж. Х.; Кларк, CE; Фазар, В. (сентябрь – октябрь 1958 г.). «Применение методики оценки программ исследований и разработок». Исследование операций . 7 (5): 646–669. дои : 10.1287/opre.7.5.646 . ISSN 0030-364X .
- ↑ Перейти обратно: Перейти обратно: а б с д Дэвид, Х.А., Нагараджа, Х.Н. (2003) Статистика заказов (3-е издание). Уайли, Нью-Джерси, стр. 458. ISBN 0-471-38926-9
- ^ «Бета-распределение» . www.statlect.com .
- ^ «1.3.6.6.17. Бета-дистрибутив» . www.itl.nist.gov .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час Элдертон, Уильям Пэйлин (1906). Частотные кривые и корреляция . Чарльз и Эдвин Лейтон (Лондон).
- ^ Элдертон, Уильям Пэйлин и Норман Ллойд Джонсон (2009). Системы частотных кривых . Издательство Кембриджского университета. ISBN 978-0521093361 .
- ↑ Перейти обратно: Перейти обратно: а б с Боуман, КО ; Шентон, ЛР (2007). «Бета-распределение, метод моментов, Карл Пирсон и Р.А. Фишер» (PDF) . Дальний Восток Дж. Тео. Стат . 23 (2): 133–164.
- ↑ Перейти обратно: Перейти обратно: а б Пирсон, Карл (июнь 1936 г.). «Метод моментов и метод максимального правдоподобия». Биометрика . 28 (1/2): 34–59. дои : 10.2307/2334123 . JSTOR 2334123 .
- ↑ Перейти обратно: Перейти обратно: а б с Джоанс, Д.Н.; Калифорния Гилл (1998). «Сравнение показателей асимметрии выборки и эксцесса». Статистик . 47 (Часть 1): 183–189. дои : 10.1111/1467-9884.00122 .
- ^ Бекман, Р.Дж.; Г.Л. Титджен (1978). «Оценка максимального правдоподобия для бета-распределения». Журнал статистических вычислений и моделирования . 7 (3–4): 253–258. дои : 10.1080/00949657808810232 .
- ^ Гнанадэсикан Р., Пинкхэм и Хьюз (1967). «Оценка максимального правдоподобия параметров бета-распределения по статистике наименьшего порядка». Технометрика . 9 (4): 607–620. дои : 10.2307/1266199 . JSTOR 1266199 .
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Факлер, Пол. «Обратная дигамма-функция (Matlab)» . Школа инженерии и прикладных наук Гарвардского университета . Проверено 18 августа 2012 г.
- ↑ Перейти обратно: Перейти обратно: а б с Сильви, SD (1975). Статистический вывод . Чепмен и Хэл. п. 40. ИСБН 978-0412138201 .
- ^ Эдвардс, AWF (1992). Вероятность . Издательство Университета Джонса Хопкинса. ISBN 978-0801844430 .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж Джейнс, ET (2003). Теория вероятностей, логика науки . Издательство Кембриджского университета. ISBN 978-0521592710 .
- ^ Коста, Макс, и Ковер, Томас (сентябрь 1983 г.). О сходстве энтропийного степенного неравенства и неравенства Брунна Минковского (PDF) . Технический отчет 48, Статистический факультет Стэнфордского университета.
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ↑ Перейти обратно: Перейти обратно: а б с Арьял, Гокарна; Саралис Надараджа (2004). «Информационная матрица для бета-распределений» (PDF) . Математический журнал Сердика (Болгарская академия наук) . 30 : 513–526.
- ↑ Перейти обратно: Перейти обратно: а б Лаплас, Пьер Симон, маркиз де (1902). Философское эссе о вероятностях . Нью-Йорк: Дж. Уайли; Лондон: Чепмен и Холл. ISBN 978-1-60206-328-0 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Кокс, Ричард Т. (1961). Алгебра вероятного вывода . Издательство Университета Джонса Хопкинса. ISBN 978-0801869822 .
- ↑ Перейти обратно: Перейти обратно: а б Кейнс, Джон Мейнард (2010) [1921]. Трактат о вероятности: связь между философией и историей науки . Уайлдсайд Пресс. ISBN 978-1434406965 .
- ^ Пирсон, Карл (1907). «О влиянии прошлого опыта на ожидания будущего». Философский журнал . 6 (13): 365–378.
- ↑ Перейти обратно: Перейти обратно: а б с д Джеффрис, Гарольд (1998). Теория Вероятностей . Издательство Оксфордского университета, 3-е издание. ISBN 978-0198503682 .
- ^ Броуд, CD (октябрь 1918 г.). «О связи индукции и вероятности». РАЗУМ, Ежеквартальный обзор психологии и философии . 27 (Новая серия) (108): 389–404. дои : 10.1093/mind/XXVII.4.389 . JSTOR 2249035 .
- ↑ Перейти обратно: Перейти обратно: а б с д Перкс, Уилфред (январь 1947 г.). «Некоторые наблюдения об обратной вероятности, включая новое правило безразличия» . Журнал Института актуариев . 73 (2): 285–334. дои : 10.1017/S0020268100012270 . Архивировано из оригинала 12 января 2014 г. Проверено 19 сентября 2012 г.
- ↑ Перейти обратно: Перейти обратно: а б Байес, Томас; сообщил Ричард Прайс (1763). «Очерк решения проблемы учения о шансах» . Философские труды Королевского общества . 53 : 370–418. дои : 10.1098/rstl.1763.0053 . JSTOR 105741 .
- ^ Холдейн, JBS (1932). «Заметка об обратной вероятности». Математические труды Кембриджского философского общества . 28 (1): 55–61. Бибкод : 1932PCPS...28...55H . дои : 10.1017/s0305004100010495 . S2CID 122773707 .
- ^ Зеллнер, Арнольд (1971). Введение в байесовский вывод в эконометрике . Уайли-Интерсайенс. ISBN 978-0471169376 .
- ^ Джеффрис, Гарольд (сентябрь 1946 г.). «Инвариантная форма априорной вероятности в задачах оценки» . Труды Королевского общества . А 24. 186 (1007): 453–461. Бибкод : 1946RSPSA.186..453J . дои : 10.1098/rspa.1946.0056 . ПМИД 20998741 .
- ^ Бергер, Джеймс; Бернардо, Хосе; Сунь, Дунчу (2009). «Формальное определение эталонных априоров» . Анналы статистики . 37 (2): 905–938. arXiv : 0904.0156 . Бибкод : 2009arXiv0904.0156B . дои : 10.1214/07-AOS587 . S2CID 3221355 .
- ^ Кларк, Бертран С.; Эндрю Р. Бэррон (1994). «Приор Джеффриса асимптотически наименее благоприятен с точки зрения энтропийного риска» (PDF) . Журнал статистического планирования и выводов . 41 : 37–60. дои : 10.1016/0378-3758(94)90153-8 .
- ^ Пирсон, Карл (1892). Грамматика науки . Вальтер Скотт, Лондон.
- ^ Пирсон, Карл (2009). Грамматика науки . БиблиоЛайф. ISBN 978-1110356119 .
- ^ Гельман А., Карлин Дж. Б., Стерн Х. С. и Рубин Д. Б. (2003). Байесовский анализ данных . Чепмен и Холл/CRC. ISBN 978-1584883883 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ А. Ёсанг. Логика неопределенных вероятностей. Международный журнал неопределенности, нечеткости и систем, основанных на знаниях . 9(3), стр.279–311, июнь 2001 г. PDF [ постоянная мертвая ссылка ]
- ^ HM de Oliveira и GAA Araújo. Одноциклические вейвлеты с компактной поддержкой, полученные на основе бета-распределений. Журнал коммуникаций и информационных систем. том 20, №3, стр.27-33, 2005.
- ^ Болдинг, Дэвид Дж .; Николс, Ричард А. (1995). «Метод количественной оценки дифференциации популяций по многоаллельным локусам и его значение для исследования идентичности и отцовства». Генетика . 96 (1–2). Спрингер: 3–12. дои : 10.1007/BF01441146 . ПМИД 7607457 . S2CID 30680826 .
- ^ Кифер, Дональд Л. и Вердини, Уильям А. (1993). Лучшая оценка параметров времени активности PERT. Наука управления 39(9), с. 1086–1091.
- ^ Кифер, Дональд Л. и Бодили, Сэмюэл Э. (1983). Трехточечные аппроксимации для непрерывных случайных величин. Наука управления 29(5), с. 595–609.
- ^ «Институт управления оборонными ресурсами – Военно-морская аспирантура» . www.nps.edu .
- ^ ван дер Варден, Б.Л., «Математическая статистика», Springer, ISBN 978-3-540-04507-6 .
- ^ О нормализации неполной бета-функции для подгонки к кривым «доза-эффект» ME Wise Biometrika, том 47, № 1/2, июнь 1960 г., стр. 173–175.
- ^ Юл, ГУ ; Филон, СПГ (1936 г.). «Карл Пирсон. 1857–1936» . Некрологи членов Королевского общества . 2 (5): 72. дои : 10.1098/rsbm.1936.0007 . JSTOR 769130 .
- ^ «Библиотечно-архивный каталог» . Цифровой архив Саклера . Королевское общество. Архивировано из оригинала 25 октября 2011 г. Проверено 1 июля 2011 г.
- ^ Дэвид, HA и AWF Эдвардс (2001). Аннотированные чтения по истории статистики . Спрингер; 1 издание. ISBN 978-0387988443 .
- ^ Джини, Коррадо (1911). «Соображения апостериорной вероятности и их применение к соотношению полов при рождении человека». Экономико-правовые исследования Университета Кальяри . Год III (воспроизведено в Metron 15, 133, 171, 1949): 5–41.
- ^ Джонсон, Норман Л. и Сэмюэл Коц, изд. (1997). Ведущие деятели статистических наук: от семнадцатого века до наших дней (Серия Wiley по вероятности и статистике . Wiley. ISBN 978-0471163817 .
- ^ Журнал Метрон. «Биография Коррадо Джини» . Журнал Метрон. Архивировано из оригинала 16 июля 2012 г. Проверено 18 августа 2012 г.
Внешние ссылки [ править ]
- «Бета-распределение» , Фиона Маклахлан, Демонстрационный проект Wolfram , 2007 г.
- Бета-дистрибутив – обзор и пример , xycoon.com
- Бета-распространение , Brighton-webs.co.uk
- Видео о бета-раздаче , exstrom.com
- «Бета-распределение» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Вайсштейн, Эрик В. «Бета-распределение» . Математический мир .
- Статистика Гарвардского университета 110 Лекция 23 Бета-распределение, профессор Джо Блицштейн
![{\displaystyle x\in [0,1]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09601f74a28f3e2cad381be1a915ab0c02fe39c6)





![{\displaystyle \operatorname {E} [X]={\frac {\alpha }{\alpha +\beta }}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3905662ceed484cba5580951e29eda96f4d2605e)
![{\displaystyle \operatorname {E} [\ln X]=\psi (\alpha)-\psi (\alpha +\beta)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de67df996fa33237ab7f415e7edc9fa8e71997a0)
![{\displaystyle \operatorname {E} [X\,\ln X]= {\frac {\alpha }{\alpha +\beta }}\,\left[\psi (\alpha +1)-\psi (\ альфа +\бета +1)\вправо]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50106a787db7d72ce3066a5a3238813cffebcc2e)

![{\displaystyle {\begin{matrix}I_{\frac {1}{2}}^{[-1]}(\alpha,\beta){\text{ (в общем) }}\\[0.5em] \approx {\frac {\alpha -{\tfrac {1}{3}}}{\alpha +\beta -{\tfrac {2}{3}}}}{\text{ for }}\alpha ,\ бета >1\end{матрица}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af887ef0331cde970dad14ad670cf3592334f845)


![{\displaystyle \operatorname {var} [X]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90a6ad61b4b436749ca37a6c2a1aa077b032ce3)
![{\displaystyle \operatorname {var} [\ln X]=\psi _{1}(\alpha)-\psi _{1}(\alpha +\beta)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4941f45412823abd34d3befea7f8fbf544135e4)

![{\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\альфа +\бета +2)(\альфа +\бета +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea65a8d7c9e00ba6299b727eab679117776f41e)
![{\displaystyle {\begin{matrix}\ln \mathrm {B} (\alpha,\beta)-(\alpha -1)\psi (\alpha)-(\beta -1)\psi (\beta)\ \[0.5em]{}+(\alpha +\beta -2)\psi (\alpha +\beta )\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff4b6cc1848fe96318adb734393b701cb816f88a)


![{\displaystyle {\begin{bmatrix}\operatorname {var} [\ln X]&\operatorname {cov} [\ln X,\ln(1-X)]\\\operatorname {cov} [\ln X, \ln(1-X)]&\operatorname {var} [\ln(1-X)]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/881f91af0ab1d6bf3809a4ed6ca9e6384544292f)
}{V[X]}}-1\right)E[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b596a180ef813a0baa1d6f2063950e20da1f62)
}{V[X]}}-1\right)(1-E[X])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ace15e23f6ac9be43eea861f44c018fd3d00de)






![{\displaystyle {\begin{aligned}f(x;\alpha,\beta) &=\mathrm {constant} \cdot x^{\alpha -1}(1-x)^{\beta -1}\\ [3pt]&={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\displaystyle \int _{0}^{1}u^{\alpha -1 }(1-u)^{\beta -1}\,du}}\\[6pt]&={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\ beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\\[6pt]&={\frac {1}{\mathrm {B} (\alpha,\ бета )}}x^{\alpha -1}(1-x)^{\beta -1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc18388353b219c482e8e35ca4aae808ab1be81)































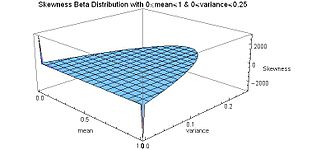

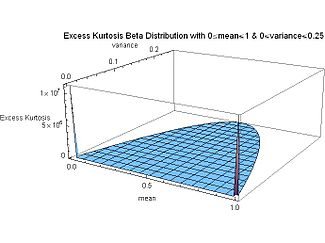





![{\displaystyle {\begin{aligned}\mu _{Y} &=\mu _{X}(ca)+a\\&=\left({\frac {\alpha }{\alpha +\beta }} \right)(ca)+a={\frac {\alpha c+\beta a}{\alpha +\beta }}\\[8pt]{\text{mode}}(Y)&={\text{mode }}(X)(ca)+a\\&=\left({\frac {\alpha -1}{\alpha +\beta -2}}\right)(ca)+a={\frac {( \alpha -1)c+(\beta -1)a}{\alpha +\beta -2}}\ ,\qquad {\text{ if }}\alpha ,\beta >1\\[8pt]{\text {медиана}}(Y)&={\text{медиана}}(X)(ca)+a\\&=\left(I_{\frac {1}{2}}^{[-1]}( \alpha ,\beta )\right)(ca)+a\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f65af6c528ca47e8838d3d5722a94f9e3f128100)





![{\displaystyle {\text{избыток эксцесса}}(Y)={\text{избыток эксцесса}}(X)={\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99ddb3577b02ee0b10163123af23c6d7f728946b)

![{\displaystyle x=I_{1/2}^{[-1]}(\альфа,\бета)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7510f94efa49f254eb3924678b527a6fd22d0fc)





![Abs[(Median-Appr.)/Median] для бета-распределения для 1 ≤ α ≤ 5 и 1 ≤ β ≤ 5](http://upload.wikimedia.org/wikipedia/commons/thumb/a/af/Relative_Error_for_Approximation_to_Median_of_Beta_Distribution_for_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg/325px-Relative_Error_for_Approximation_to_Median_of_Beta_Distribution_for_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg)
![Abs[(Mean-Appr.)/(Mean-Mode)] для бета-распределения для 1妻α可5 и 1可β可5](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e8/Error_in_Median_Apprx._relative_to_Mean-Mode_distance_for_Beta_Distribution_with_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg/325px-Error_in_Median_Apprx._relative_to_Mean-Mode_distance_for_Beta_Distribution_with_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg)
![{\displaystyle {\begin{aligned}\mu =\operatorname {E} [X]&=\int _{0}^{1}xf(x;\alpha,\beta)\,dx\\&=\ int _{0}^{1}x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha,\beta) }}\,dx\\&={\frac {\alpha }{\alpha +\beta }}\\&={\frac {1}{1+{\frac {\beta }{\alpha }}} }\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9137834d9d47360ed6c23550c6236fed5fd35f7)


![{\displaystyle \ln G_{X}=\operatorname {E} [\ln X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64b67cb73b90bc0e09ba41003b44f84b6e1d3feb)
![{\displaystyle {\begin{aligned}\operatorname {E} [\ln X]&=\int _{0}^{1}\ln x\,f(x;\alpha,\beta)\,dx\ \[4pt]&=\int _{0}^{1}\ln x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm { B} (\alpha,\beta)}}\,dx\\[4pt]&={\frac {1}{\mathrm {B} (\alpha,\beta)}}\,\int _{0} ^{1}{\frac {\partial x^{\alpha -1}(1-x)^{\beta -1}}{\partial \alpha }}\,dx\\[4pt]&={\ frac {1}{\mathrm {B} (\alpha ,\beta )}}{\frac {\partial }{\partial \alpha }}\int _{0}^{1}x^{\alpha -1 }(1-x)^{\beta -1}\,dx\\[4pt]&={\frac {1}{\mathrm {B} (\alpha,\beta )}}{\frac {\partial \mathrm {B} (\alpha,\beta)}{\partial \alpha }}\\[4pt]&={\frac {\partial \ln \mathrm {B} (\alpha,\beta)}{\ частичный \alpha }}\\[4pt]&={\frac {\partial \ln \Gamma (\alpha )}{\partial \alpha }}-{\frac {\partial \ln \Gamma (\alpha +\ beta )}{\partial \alpha }}\\[4pt]&=\psi (\alpha )-\psi (\alpha +\beta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd9db519e08e3c72cd6f9e2f0c90a7c57bdba035)
![{\displaystyle G_{X}=e^{\operatorname {E} [\ln X]}=e^{\psi (\alpha)-\psi (\alpha +\beta)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c93ffa7f0155fa3816fcb151c3eb677700aabca2)




![{\displaystyle G_{(1-X)}=e^{\operatorname {E} [\ln(1-X)]}=e^{\psi (\beta)-\psi (\alpha +\beta) }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8013e6a62bd5140a4e7919686761225dd54847e)




![{\displaystyle {\begin{aligned}H_{X}&={\frac {1}{\operatorname {E} \left[{\frac {1}{X}}\right]}}\\&={ \frac {1}{\int _{0}^{1}{\frac {f(x;\alpha ,\beta )}{x}}\,dx}}\\&={\frac {1} {\int _{0}^{1}{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{x\mathrm {B} (\alpha,\beta) }}\,dx}}\\&={\frac {\alpha -1}{\alpha +\beta -1}}{\text{ if }}\alpha >1{\text{ и }}\beta >0\\\конец{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed7d99dd7493b9c085cd5d407861730e2a2abf6c)


![{\displaystyle H_{1-X}={\frac {1}{\operatorname {E} \left[{\frac {1}{1-X}}\right]}}={\frac {\beta - 1}{\alpha +\beta -1}}{\text{ if }}\beta >1,{\text{ и }}\alpha >0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48f4fd69f20c4259cb8a50e754df8dfed5a1ddca)



![{\displaystyle \operatorname {var} (X)=\operatorname {E} [(X-\mu)^{2}]={\frac {\alpha \beta }{(\alpha +\beta)^{2 }(\альфа +\бета +1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96555f71897dc80e2f31ec71b3cbfbcf39950bc)






![{\displaystyle {\begin{aligned}\ln \operatorname {var} _{GX}&=\operatorname {E} \left[(\ln X-\ln G_{X})^{2}\right]\ \&=\operatorname {E} [(\ln X-\operatorname {E} \left[\ln X])^{2}\right]\\&=\operatorname {E} \left[(\ln X )^{2}\right]-(\operatorname {E} [\ln X])^{2}\\&=\operatorname {var} [\ln X]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5737429860855b238c6ac72ae064e4bb6d8cb772)
![{\displaystyle \operatorname {var} _{GX}=e^{\operatorname {var} [\ln X]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/524cf664ccfd5eb381fd1987926209f1c401a200)
![{\displaystyle {\begin{aligned}\ln \operatorname {var_{G(1-X)}} &=\operatorname {E} [(\ln(1-X)-\ln G_{1-X}) ^{2}]\\&=\operatorname {E} [(\ln(1-X)-\operatorname {E} [\ln(1-X)])^{2}]\\&=\operatorname {E} [(\ln(1-X))^{2}]-(\operatorname {E} [\ln(1-X)])^{2}\\&=\operatorname {var} [\ ln(1-X)]\\&\\\operatorname {var_{G(1-X)}} &=e^{\operatorname {var} [\ln(1-X)]}\\&\\ \ln \operatorname {cov_{G{X,1-X}}} &=\operatorname {E} [(\ln X-\ln G_{X})(\ln(1-X)-\ln G_{ 1-X})]\\&=\operatorname {E} [(\ln X-\operatorname {E} [\ln X])(\ln(1-X)-\operatorname {E} [\ln( 1-X)])]\\&=\operatorname {E} \left[\ln X\ln(1-X)\right]-\operatorname {E} [\ln X]\operatorname {E} [\ ln(1-X)]\\&=\operatorname {cov} [\ln X,\ln(1-X)]\\&\\\operatorname {cov} _{G{X,(1-X) }}&=e^{\operatorname {cov} [\ln X,\ln(1-X)]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9951a17fba87115b493918bfd9271c8e2193d0a8)
![{\displaystyle \operatorname {var} [\ln X]=\psi _{1}(\alpha)-\psi _{1}(\alpha +\beta)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e396e8700267735eb741f73e8906445579c43bc6)
![{\displaystyle \operatorname {var} [\ln(1-X)]=\psi _{1}(\beta)-\psi _{1}(\alpha +\beta)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70eefadef46c7d56cc13c8221aa3df1d71596b7f)
![{\displaystyle \operatorname {cov} [\ln X,\ln(1-X)]=-\psi _{1}(\alpha +\beta)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7a515ada0b9d62c5a3a7b35662b03256d66e3b9)

![{\displaystyle \ln \operatorname {var} _{GX} = \operatorname {var} [\ln X]=\psi _{1}(\alpha)-\psi _{1}(\alpha +\beta) }](https://wikimedia.org/api/rest_v1/media/math/render/svg/194b00552edda5d8d026a24872cdb27b604516c9)
![{\displaystyle \ln \operatorname {var} _{G(1-X)} = \operatorname {var} [\ln(1-X)]=\psi _{1}(\beta)-\psi _{ 1}(\альфа +\бета)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96dd82553307c025c84da68a3c373aad7467abd2)
![{\displaystyle \ln \operatorname {cov} _{GX,1-X} = \operatorname {cov} [\ln X,\ln(1-X)]=-\psi _{1}(\alpha +\ бета )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a793c0271e457f671edb0668edc15bbae8740f)




![{\displaystyle \operatorname {E} [|XE[X]|]={\frac {2\alpha ^{\alpha }\beta ^{\beta }}{\mathrm {B} (\alpha,\beta) (\alpha +\beta )^{\alpha +\beta +1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d1c6330a91df22b40cedc7903dbc70120d66cf9)
![{\displaystyle {\begin{aligned}{\frac {\text{среднее абс. разработчик от среднего}}{\text{стандартное отклонение}}}&={\frac {\operatorname {E} [|XE[X]|]}{\sqrt {\operatorname {var} (X)}}}\\ &\approx {\sqrt {\frac {2}{\pi }}}\left(1+{\frac {7}{12(\alpha +\beta )}}{}-{\frac {1}{ 12\alpha }}-{\frac {1}{12\beta }}\right),{\text{ if }}\alpha ,\beta >1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c196a5a2eb110b71471a3dc019241c6cb8c3f927)


![{\displaystyle \operatorname {E} [|XE[X]|]={\frac {2\mu ^{\mu }(1-\mu )^{(1-\mu )\nu }}{ \from \mathrm {B} (\from ,(1-\f )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027efecf8aaefea8c805194e47a1374ffcb63cb8)
![{\displaystyle {\begin{aligned}\operatorname {E} [|XE[X]|]={\frac {2^{1-\nu }}{\nu \mathrm {B} ({\tfrac {\ nu }{2}},{\tfrac {\nu }{2}})}}&={\frac {2^{1-\nu }\Gamma (\nu )}{\nu (\Gamma ({ \tfrac {\nu }{2}}))^{2}}}\\\lim _{\nu \to 0}\left(\lim _{\mu \to {\frac {1}{2} }}\operatorname {E} [|XE[X]|]\right)&={\tfrac {1}{2}}\\\lim _{\nu \to \infty }\left(\lim _{ \mu \to {\frac {1}{2}}}\operatorname {E} [|XE[X]|]\right)&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87aa0eff7a4da0f5abe2d211e2b7dda8c8fff801)
![{\displaystyle {\begin{aligned}\lim _ {\beta \to 0}\operatorname {E} [|XE[X]|]&=\lim _ {\alpha \to 0}\operatorname {E} [ |XE[X]|]=0\\\lim _{\beta \to \infty }\operatorname {E} [|XE[X]|]&=\lim _{\alpha \to \infty }\operatorname {E} [|XE[X]|]=0\\\lim _{\mu \to 0}\operatorname {E} [|XE[X]|]&=\lim _{\mu \to 1} \operatorname {E} [|XE[X]|]=0\\\lim _{\nu \to 0}\operatorname {E} [|XE[X]|]&={\sqrt {\mu (1 -\mu )}}\\\lim _{\nu \to \infty }\operatorname {E} [|XE[X]|]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87c43b4a05f8ea3acf3f15b0a16f6ee07811ac6b)


![{\displaystyle \gamma _{1}={\frac {\operatorname {E} [(X-\mu )^{3}]}{(\operatorname {var} (X))^{3/2}} }={\frac {2(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2334c6fa1e6326760870b716521460bba115a92)

![{\displaystyle \gamma _{1}={\frac {\operatorname {E} [(X-\mu )^{3}]}{(\operatorname {var} (X))^{3/2}} }={\frac {2(1-2\mu ){\sqrt {1+\nu }}}{(2+\nu ){\sqrt {\mu (1-\mu )}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d71042628a42bfedc972e01f8ba5c27f63c3fae4)
![{\displaystyle \gamma _{1}={\frac {\operatorname {E} [(X-\mu )^{3}]}{(\operatorname {var} (X))^{3/2}} }={\frac {2(1-2\mu ){\sqrt {\text{ var }}}}{\mu (1-\mu )+\operatorname {var} }}{\text{ if }} \operatorname {var} <\mu (1-\mu )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e30c818c1af07028336494d35562333ffd903f1)
![{\displaystyle (\gamma _{1})^{2}={\frac {(\operatorname {E} [(X-\mu )^{3}])^{2}}{(\operatorname {var } (X))^{3}}}={\frac {4}{(2+\nu )^{2}}}{\bigg (}{\frac {1}{\text{var}}} -4(1+\nu ){\bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d9343b5e45ab6ac483a8f0fb8efd1699e0158d)





![{\displaystyle {\begin{aligned}{\text{избыточный эксцесс}}&={\text{эксцесс}}-3\\&={\frac {\operatorname {E} [(X-\mu )^{ 4}]}{(\operatorname {var} (X))^{2}}}-3\\&={\frac {6[\alpha ^{3}-\alpha ^{2}(2\beta -1)+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}\\&={\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)] }{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed8320d4f38ba9260f8ad91c30238abc08306dc8)











![{\displaystyle {\begin{aligned}\varphi _{X}(\alpha;\beta;t)&=\operatorname {E} \left[e^{itX}\right]\\&=\int _{ 0}^{1}e^{itx}f(x;\alpha ,\beta )\,dx\\&={}_{1}F_{1}(\alpha ;\alpha +\beta ;it) \!\\&=\sum _{n=0}^{\infty }{\frac {\alpha ^{(n)}(it)^{n}}{(\alpha +\beta )^{( n)}n!}}\\&=1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha + r}{\alpha +\beta +r}}\right){\frac {(it)^{k}}{k!}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dac7a59df675d0b8758523c87e85888609a213c)


![{\displaystyle \operatorname {Re} \left[{}_{1}F_{1}(\alpha;\alpha +\beta;it)\right]=\operatorname {Re} \left[{}_{1 }F_{1}(\alpha ;\alpha +\beta ;-it)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/468f2135d76bd1b522c84092679209ff6abd5845)
![{\displaystyle \operatorname {Im} \left[{}_{1}F_{1}(\alpha;\alpha +\beta;it)\right]=-\operatorname {Im} \left[{}_{ 1}F_{1}(\alpha ;\alpha +\beta ;-it)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fca8984292cc85cb8a37ecb5a2b7c04b5596282)


![{\displaystyle {\begin{aligned}M_{X}(\alpha;\beta;t)&=\operatorname {E} \left[e^{tX}\right]\\[4pt]&=\int _ {0}^{1}e^{tx}f(x;\alpha ,\beta )\,dx\\[4pt]&={}_{1}F_{1}(\alpha ;\alpha +\ beta ;t)\\[4pt]&=\sum _{n=0}^{\infty }{\frac {\alpha ^{(n)}}{(\alpha +\beta )^{(n) }}}{\frac {t^{n}}{n!}}\\[4pt]&=1+\sum _{k=1}^{\infty }\left(\prod _{r=0 }^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}.\end{aligned} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e664dd90aeae487c19dc89c87c7d1abe47bfcf3d)


![{\displaystyle \operatorname {E} [X^{k}]={\frac {\alpha ^{(k)}}{(\alpha +\beta )^{(k)}}}=\prod _{ r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e03c03f31b903a1bc73ea8b637e3134b110a85a2)
![{\displaystyle \operatorname {E} [X^{k}]={\frac {\alpha +k-1}{\alpha +\beta +k-1}}\operatorname {E} [X^{k- 1}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/069cb373a905b1e8a5a82a0e3b028e88f63672e2)

![{\displaystyle {\begin{aligned}\operatorname {E} [1-X]&= {\frac {\beta }{\alpha +\beta }}\\\operatorname {E} [X(1-X) ]&=\operatorname {E} [(1-X)X]={\frac {\alpha \beta }{(\alpha +\beta )(\alpha +\beta +1)}}\end{aligned} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fc49b9eafccd56d39c236b26d222dde51638ce)
![{\displaystyle \operatorname {var} [(1-X)]=\operatorname {var} [X]=-\operatorname {cov} [X,(1-X)]= {\frac {\alpha \beta } {(\альфа +\бета )^{2}(\альфа +\бета +1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7273cc84a6c789724b985c34059fa75a62bce631)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[{\frac {1}{X}}\right]&={\frac {\alpha +\beta -1}{\alpha -1} }&&{\text{ if }}\alpha >1\\\operatorname {E} \left[{\frac {1}{1-X}}\right]&={\frac {\alpha +\beta - 1}{\beta -1}}&&{\text{ if }}\beta >1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972a9c1853e6991aac6666b06c0a633a0caad5b7)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[{\frac {X}{1-X}}\right]&={\frac {\alpha }{\beta -1}}&& { \text{ if }}\beta >1\\\operatorname {E} \left[{\frac {1-X}{X}}\right]&={\frac {\beta }{\alpha -1} }&&{\text{ if }}\alpha >1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db2a0928a7f906bcbe5cfd9d0c57713c9ab5cfb7)
![{\displaystyle \operatorname {var} \left[{\frac {1}{X}}\right]=\operatorname {E} \left[\left({\frac {1}{X}}-\operatorname { E} \left[{\frac {1}{X}}\right]\right)^{2}\right]=\operatorname {var} \left[{\frac {1-X}{X}}\ right]=\operatorname {E} \left[\left({\frac {1-X}{X}}-\operatorname {E} \left[{\frac {1-X}{X}}\right] \right)^{2}\right]={\frac {\beta (\alpha +\beta -1)}{(\alpha -2)(\alpha -1)^{2}}}{\text{ если }}\альфа >2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af7a7cb782c6c42658374ac45365cde388c2326a)
![{\displaystyle \operatorname {var} \left[{\frac {1}{1-X}} \right]=\operatorname {E} \left[\left({\frac {1}{1-X}} -\operatorname {E} \left[{\frac {1}{1-X}}\right]\right)^{2}\right]=\operatorname {var} \left[{\frac {X}{ 1-X}}\right]=\operatorname {E} \left[\left({\frac {X}{1-X}}-\operatorname {E} \left[{\frac {X}{1- X}}\right]\right)^{2}\right]={\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2} }}{\text{ if }}\beta >2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22dd8c7aad68227962947ad69019b01a79c41b6d)
![{\displaystyle \operatorname {cov} \left[{\frac {1}{X}}, {\frac {1}{1-X}}\right]=\operatorname {cov} \left[{\frac { 1-X}{X}},{\frac {X}{1-X}}\right]=\operatorname {cov} \left[{\frac {1}{X}},{\frac {X} {1-X}}\right]=\operatorname {cov} \left[{\frac {1-X}{X}},{\frac {1}{1-X}}\right]={\frac {\alpha +\beta -1}{(\alpha -1)(\beta -1)}}{\text{ if }}\alpha ,\beta >1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa2342c3fe24a7ed5b840fd9583c055aa5791486)
![{\displaystyle {\begin{aligned}\operatorname {E} [\ln(X)]&=\psi (\alpha)-\psi (\alpha +\beta)=-\operatorname {E} \left[\ ln \left({\frac {1}{X}}\right)\right],\\\operatorname {E} [\ln(1-X)]&=\psi (\beta )-\psi (\ альфа +\beta )=-\operatorname {E} \left[\ln \left({\frac {1}{1-X}}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6125bcdc7551c82f7451b444b941c97b83abdf20)

![{\displaystyle {\begin{aligned}\operatorname {E} \left[\ln \left({\frac {X}{1-X}}\right)\right]&=\psi (\alpha)-\ psi (\beta )=\operatorname {E} [\ln(X)]+\operatorname {E} \left[\ln \left({\frac {1}{1-X}}\right)\right] ,\\\operatorname {E} \left[\ln \left({\frac {1-X}{X}}\right)\right]&=\psi (\beta )-\psi (\alpha )= -\operatorname {E} \left[\ln \left({\frac {X}{1-X}}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/519d77a6f894b5ebc9240b813a675477194f8858)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[\ln ^{2}(X)\right]&=(\psi (\alpha)-\psi (\alpha +\beta))^ {2}+\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta ),\\\operatorname {E} \left[\ln ^{2}(1-X) \right]&=(\psi (\beta )-\psi (\alpha +\beta ))^{2}+\psi _{1}(\beta )-\psi _{1}(\alpha +\ beta ),\\\operatorname {E} \left[\ln(X)\ln(1-X)\right]&=(\psi (\alpha )-\psi (\alpha +\beta ))(\ psi (\beta )-\psi (\alpha +\beta ))-\psi _{1}(\alpha +\beta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42eb1276e349df39df3051df11e0e16afe88e2e)
![{\displaystyle {\begin{aligned}\operatorname {cov} [\ln(X),\ln(1-X)]&=\operatorname {E} \left[\ln(X)\ln(1-X) )\right]-\operatorname {E} [\ln(X)]\operatorname {E} [\ln(1-X)]=-\psi _{1}(\alpha +\beta )\\&\ \\operatorname {var} [\ln X]&=\operatorname {E} [\ln ^{2}(X)]-(\operatorname {E} [\ln(X)])^{2}\\ &=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )\\&=\psi _{1}(\alpha )+\operatorname {cov} [\ln( X),\ln(1-X)]\\&\\\operatorname {var} [\ln(1-X)]&=\operatorname {E} [\ln ^{2}(1-X)] -(\operatorname {E} [\ln(1-X)])^{2}\\&=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )\ \&=\psi _{1}(\beta )+\operatorname {cov} [\ln(X),\ln(1-X)]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e76df52180954247e1d1aa62646a20f7e3d68a36)

![{\displaystyle {\begin{aligned}\operatorname {var} \left[\ln \left({\frac {1}{X}}\right)\right]&=\operatorname {var} [\ln(X )]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta ),\\\operatorname {var} \left[\ln \left({\frac {1}{ 1-X}}\right)\right]&=\operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\ beta ),\\\operatorname {cov} \left[\ln \left({\frac {1}{X}}\right),\ln \left({\frac {1}{1-X}}\ right)\right]&=\operatorname {cov} [\ln(X),\ln(1-X)]=-\psi _{1}(\alpha +\beta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d335167cf1713083b3fb1c4d0cfadb04c1d40d43)
![{\displaystyle \operatorname {var} \left[\ln \left({\frac {X}{1-X}}\right)\right]=\operatorname {var} \left[\ln \left({\ frac {1-X}{X}}\right)\right]=-\operatorname {cov} \left[\ln \left({\frac {X}{1-X}}\right),\ln \ left({\frac {1-X}{X}}\right)\right]=\psi _{1}(\alpha )+\psi _{1}(\beta ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52585d88405196366b14e2e7183f48be9b5de874)
![{\displaystyle {\begin{aligned}h(X)&=\operatorname {E} [-\ln(f(x;\alpha,\beta))]\\[4pt]&=\int _{0} ^{1}-f(x;\alpha ,\beta )\ln(f(x;\alpha ,\beta ))\,dx\\[4pt]&=\ln(\mathrm {B} (\alpha ,\beta ))-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )+(\alpha +\beta -2)\psi (\alpha +\beta ) \end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc995dbbf41c91536ce4d0efaff554d8b0a77fe)



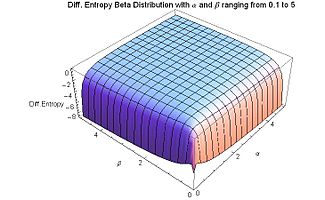
![{\displaystyle {\begin{aligned}H(X_{1},X_{2}) &=\int _{0}^{1}-f(x;\alpha,\beta)\ln(f(x) ;\alpha ',\beta '))\,dx\\[4pt]&=\ln \left(\mathrm {B} (\alpha ',\beta ')\right)-(\alpha '-1) \psi (\alpha )-(\beta '-1)\psi (\beta )+(\alpha '+\beta '-2)\psi (\alpha +\beta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711e6ef61e56ccd8ba515b8db5013d1847939ec8)
![{\displaystyle {\begin{aligned}D_{\mathrm {KL} }(X_{1}\parallel X_{2})&=\int _{0}^{1}f(x;\alpha,\beta )\ln \left({\frac {f(x;\alpha ,\beta )}{f(x;\alpha ',\beta ')}}\right)\,dx\\[4pt]&=\ left(\int _{0}^{1}f(x;\alpha ,\beta )\ln(f(x;\alpha ,\beta ))\,dx\right)-\left(\int _{ 0}^{1}f(x;\alpha ,\beta )\ln(f(x;\alpha ',\beta '))\,dx\right)\\[4pt]&=-h(X_{ 1})+H(X_{1},X_{2})\\[4pt]&=\ln \left({\frac {\mathrm {B} (\alpha ',\beta ')}{\mathrm {B} (\alpha ,\beta )}}\right)+(\alpha -\alpha ')\psi (\alpha )+(\beta -\beta ')\psi (\beta )+(\alpha ' -\alpha +\beta '-\beta )\psi (\alpha +\beta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d62cb13ae214eaa48e12d453fbae8bdd58b301a)



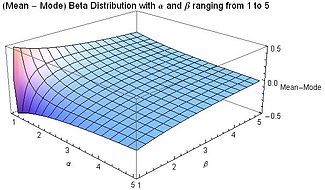














![{\displaystyle \operatorname {E} [|XE[X]|](\mathrm {B} (\alpha,\beta))=\operatorname {E} [|XE[X]|](\mathrm {B} (\бета,\альфа))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83468b7365d9095b07e04bfbb5c9cff50c64ea2d)


![{\displaystyle {\text{Re}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)]={\text{Re}}[{}_{1}F_ {1}(\альфа ;\альфа +\бета ;-it)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bbddff6ec53eb39eccc603618459ba36e10ad2)
![{\displaystyle {\text{Im}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)]=- {\text{Im}}[{}_{1} F_{1}(\альфа ;\альфа +\бета ;-it)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebb682c9915a60ef8d982340de042127ab262a0f)
![{\displaystyle {\text{Abs}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)]={\text{Abs}}[{}_{1}F_ {1}(\альфа ;\альфа +\бета ;-it)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c1c15ff4c63020b66d2404d439514d965946d0)





































































































![{\displaystyle \operatorname {var} [\ln(X)]=\operatorname {E} [\ln ^{2}(X)]-(\operatorname {E} [\ln(X)])^{2 }=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7737d681fea7490e27f8760c6bcc8fccb154904)
![{\displaystyle \operatorname {var} [\ln(1-X)]=\operatorname {E} [\ln ^{2}(1-X)]-(\operatorname {E} [\ln(1-X) )])^{2}=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f84c3747955206cf2190c61bd7875a6cd739ac04)
![{\displaystyle \operatorname {var} [\ln(X)]>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fb5a5d0db057469fb9dad8df2902fe93e3f3b0d)
![{\displaystyle \operatorname {var} [\ln(1-X)]>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c66a5aaa8362f578beb9b141b4108138b9d21e89)



![{\displaystyle {\begin{aligned}{\hat {\operatorname {E} }}[\ln(X)]&=\psi ({\hat {\alpha }})-\psi ({\hat {\ альфа }}+{\hat {\beta }})={\frac {1}{N}}\sum _{i=1}^{N}\ln X_{i}=\ln {\hat {G }}_{X}\\{\hat {\operatorname {E} }}[\ln(1-X)]&=\psi ({\hat {\beta }})-\psi ({\hat { \alpha }}+{\hat {\beta }})={\frac {1}{N}}\sum _{i=1}^{N}\ln(1-X_{i})=\ln {\hat {G}}_{(1-X)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e43bfd770a92437c9b0bbef4c7c6ead3534eba3)













![{\displaystyle {\hat {\operatorname {E} }}\left[\ln \left({\frac {X}{1-X}}\right)\right]=\psi ({\hat {\alpha }})-\psi ({\hat {\beta }})={\frac {1}{N}}\sum _{i=1}^{N}\ln {\frac {X_{i}} {1-X_{i}}}=\ln {\hat {G}}_{X}-\ln \left({\hat {G}}_{(1-X)}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d5d9a3105854f3fe65f5a72aa4418da4a50ba11)












![{\displaystyle {\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta \mid X)}{\partial \alpha ^{2}}}=-\operatorname {var } [\ln X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/517a09a3b13d22689a3e1e400cbcab3af08e130c)
![{\displaystyle {\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta \mid X)}{\partial \beta ^{2}}}=-\operatorname {var } [\ln(1-X)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1715f50fc408ceba307005a3f9e404520edd5a20)
![{\displaystyle \mathrm {var} ({\hat {\alpha }})\geq {\frac {1}{\operatorname {var} [\ln X]}}\geq {\frac {1}{\psi _{1}({\hat {\alpha }})-\psi _{1}({\hat {\alpha }}+{\hat {\beta }})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/744f1e8421337ed7a2e6cae00fccec1eaf68e3dc)
![{\displaystyle \mathrm {var} ({\hat {\beta }})\geq {\frac {1}{\operatorname {var} [\ln(1-X)]}}\geq {\frac {1 }{\psi _{1}({\hat {\beta }})-\psi _{1}({\hat {\alpha }}+{\hat {\beta }})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f01dc5c3eb614cfa71a500fd34f3fa430c183c76)















![{\displaystyle \alpha =2:\quad \operatorname {E} \left[- {\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\ альфа,\бета,а,с\середина Y)}{\partial a^{2}}}\right]={\mathcal {I}}_{a,a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53538160a2404a5d7b74ae2033fbbb2dbc1045eb)
![{\displaystyle \beta =2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\ альфа,\бета,а,с\середина Y)}{\partial c^{2}}}\right]={\mathcal {I}}_{c,c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee2c6ecfcafe60e54799ab4a16451cf478d65f7d)
![{\displaystyle \alpha =2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\ альфа,\бета,а,с\середина Y)}{\partial \alpha \partial a}}\right]={\mathcal {I}}_{\alpha,a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b8af544d7c5e0cc278aa725daba7f3de2f70d31)
![{\displaystyle \beta =1:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\ альфа,\бета,а,с\середина Y)}{\partial \beta \partial c}}\right]={\mathcal {I}}_{\beta,c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f87b32b39997964dcbc95bc64c1364e6832db1d)
![{\displaystyle {\mathcal {I}}(\alpha)=\operatorname {E} \left[\left({\frac {\partial }{\partial \alpha }}\ln {\mathcal {L}}( \alpha \mid X)\right)^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daec13972d17a073bcd447abfde55a6b0e168720)
![{\displaystyle {\mathcal {I}}(\alpha)=-\operatorname {E} \left[{\frac {\partial ^{2}}{\partial \alpha ^{2}}}\ln({ \mathcal {L}}(\alpha \mid X))\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92244569d1fab7e801097aa25a9c883ff75be5aa)
![{\displaystyle \operatorname {var} [{\hat {\alpha }}]\geq {\frac {1}{{\mathcal {I}}(\alpha )}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d93d4983a2717258c52eb47d1562e849a3a66c5c)

![{\displaystyle ({\mathcal {I}}(\theta))_{i,j}=\operatorname {E} \left[\left({\frac {\partial }{\partial \theta _{i} }}\ln {\mathcal {L}}\right)\left({\frac {\partial }{\partial \theta _{j}}}\ln {\mathcal {L}}\right)\right] .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e4390c2c908fe7a3e4f06ee9e3526df1ff20f18)
![{\displaystyle ({\mathcal {I}}(\theta))_{i,j}=-\operatorname {E} \left[{\frac {\partial ^{2}}{\partial \theta _{ i}\,\partial \theta _{j}}}\ln({\mathcal {L}})\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b7d9fd3ec7fa358ec6450f166aa89592bcc55ab)


![{\displaystyle -{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta \mid X)}{N\partial \alpha ^{2}}}=\operatorname { var} [\ln(X)]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\alpha ,\alpha } =\operatorname {E} \left[-{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\partial \alpha ^{2} }}\right]=\ln \operatorname {var} _{GX}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c90003d5bd2f6d2bcfe2c788585689726b4b7e36)
![{\displaystyle -{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta \mid X)}{N\,\partial \beta ^{2}}}=\ имя оператора {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\beta ,\beta }=\operatorname {E} \left[-{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta \mid X)}{N\partial \beta ^{2}}}\right]=\ln \operatorname {var} _{G(1-X)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59bcc31f14f1f4b3b07bd92a66426bb6ac126b1)
![{\displaystyle -{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta \mid X)}{N\,\partial \alpha \,\partial \beta }} =\operatorname {cov} [\ln X,\ln(1-X)]=-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\alpha,\beta } =\operatorname {E} \left[-{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\,\partial \alpha \, \partial \beta }}\right]=\ln \operatorname {cov} _{G{X,(1-X)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c3268da3b23c062ce981ab02d4c454a0267365)




![{\displaystyle {\begin{aligned}\det({\mathcal {I}}(\alpha,\beta)) &={\mathcal {I}} _ {\alpha,\alpha }{\mathcal {I} } _ {\beta ,\beta }-{\mathcal {I}}_{\alpha ,\beta }{\mathcal {I}}_{\alpha ,\beta }\\[4pt]&=(\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta ))(\psi _{1}(\beta )-\psi _{1}(\alpha +\beta ))- (-\psi _{1}(\alpha +\beta ))(-\psi _{1}(\alpha +\beta ))\\[4pt]&=\psi _{1}(\alpha )\ psi _{1}(\beta )-(\psi _{1}(\alpha )+\psi _{1}(\beta ))\psi _{1}(\alpha +\beta )\\[4pt ]\lim _ {\alpha \to 0}\det({\mathcal {I}}(\alpha,\beta)) &=\lim _{\beta \to 0}\det({\mathcal {I} }(\alpha,\beta ))=\infty \\[4pt]\lim _{\alpha \to \infty }\det({\mathcal {I}}(\alpha,\beta ))&=\lim _ {\beta \to \infty }\det({\mathcal {I}}(\alpha,\beta))=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2c5ccf59b05ea730fc108360c07e9ac9634e829)

![{\displaystyle -{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\ частичный \alpha ^{2}}}=\operatorname {var} [\ln(X)]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )={\ mathcal {I}}_{\alpha ,\alpha }=\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L }}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha ^{2}}}\right]=\ln(\operatorname {var_{GX}} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31be86f2c53663c6d3975bc2676806ba3e538423)
![{\displaystyle -{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\ частичный \beta ^{2}}}=\operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )= {\mathcal {I}}_{\beta ,\beta }=\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \beta ^{2}}}\right]=\ln(\operatorname {var_{G(1-X)}} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ab885119f25fae0b9919326db96395d13e3bc3)
![{\displaystyle -{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\ частичный \alpha \,\partial \beta }}=\operatorname {cov} [\ln X,(1-X)]=-\psi _{1}(\alpha +\beta )={\mathcal {I} } _ {\alpha ,\beta }=\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\ альфа ,\beta ,a,c\mid Y)}{\partial \alpha \,\partial \beta }}\right]=\ln(\operatorname {cov} _{G{X,(1-X)} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a56af746fb9315340cf382951fe0c3f3640678)

![{\displaystyle {\begin{aligned}\alpha >2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\partial a^{2}}}\right]&={\mathcal {I}}_{a,a}={\ frac {\beta (\alpha +\beta -1)}{(\alpha -2)(ca)^{2}}}\\\beta >2:\quad \operatorname {E} \left[-{\ frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\partial c^{2} }}\right]&={\mathcal {I}}_{c,c}={\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(ca)^{2 }}}\\\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta , a,c\mid Y)}{\partial a\,\partial c}}\right]&={\mathcal {I}}_{a,c}={\frac {(\alpha +\beta -1 )}{(ca)^{2}}}\\\alpha >1:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2} \ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\partial \alpha \,\partial a}}\right]&={\mathcal {I}}_{ \alpha ,a}={\frac {\beta }{(\alpha -1)(ca)}}\\\operatorname {E} \left[-{\frac {1}{N}}{\frac { \partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\partial \alpha \,\partial c}}\right]&={\mathcal {I}}_{\alpha ,c}={\frac {1}{(ca)}}\\\operatorname {E} \left[-{\frac {1}{N}}{\frac {\ частичный ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\partial \beta \,\partial a}}\right]&={\mathcal { I}}_{\beta ,a}=-{\frac {1}{(ca)}}\\\beta >1:\quad \operatorname {E} \left[-{\frac {1}{N }}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha,\beta,a,c\mid Y)}{\partial \beta \,\partial c}}\right ]&={\mathcal {I}}_{\beta ,c}=-{\frac {\alpha }{(\beta -1)(ca)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/636646f51bdb1a3193b1721483878e98f4f19c3e)




![{\displaystyle {\mathcal {I}}_{\alpha,a}={\frac {\operatorname {E} \left[{\frac {1-X}{X}}\right]}{ca}} = {\frac {\beta }{(\alpha -1)(ca)}}{\text{ if }}\alpha >1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e670565bb8d06bace69cf892864520f5c83b5449)
![{\displaystyle {\mathcal {I}}_{\beta,c}=- {\frac {\operatorname {E} \left[{\frac {X}{1-X}}\right]}{ca} }=-{\frac {\alpha }{(\beta -1)(ca)}}{\text{ if }}\beta >1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94f9b7788a4f19e1cbc765ab8fc85a7ad55dec4f)
![{\displaystyle {\begin{aligned}\alpha >2:\quad {\mathcal {I}}_{a,a}&=\operatorname {var} \left[{\frac {1}{X}}\ right]\left({\frac {\alpha -1}{ca}}\right)^{2}=\operatorname {var} \left[{\frac {1-X}{X}}\right]\ left({\frac {\alpha -1}{ca}}\right)^{2}={\frac {\beta (\alpha +\beta -1)}{(\alpha -2)(ca)^ {2}}}\\\beta >2:\quad {\mathcal {I}}_{c,c}&=\operatorname {var} \left[{\frac {1}{1-X}}\ right]\left({\frac {\beta -1}{ca}}\right)^{2}=\operatorname {var} \left[{\frac {X}{1-X}}\right]\ left({\frac {\beta -1}{ca}}\right)^{2}={\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(ca)^ {2}}}\\{\mathcal {I}}_{a,c}&=\operatorname {cov} \left[{\frac {1}{X}},{\frac {1}{1- X}}\right]{\frac {(\alpha -1)(\beta -1)}{(ca)^{2}}}=\operatorname {cov} \left[{\frac {1-X} {X}},{\frac {X}{1-X}}\right]{\frac {(\alpha -1)(\beta -1)}{(ca)^{2}}}={\ frac {(\alpha +\beta -1)}{(ca)^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f89730020364bb58791ca0eb47d0de25c896c2)








![{\displaystyle {\begin{aligned}{\sqrt {{\mathcal {I}}(p)}}&={\sqrt {\operatorname {E} \!\left[\left({\frac {d} {dp}}\ln({\mathcal {L}}(p\mid H))\right)^{2}\right]}}\\[6pt]&={\sqrt {\operatorname {E} \ !\left[\left({\frac {H}{p}}-{\frac {1-H}{1-p}}\right)^{2}\right]}}\\[6pt]& = {\sqrt {p^{1}(1-p)^{0}\left({\frac {1}{p}}-{\frac {0}{1-p}}\right)^{ 2}+p^{0}(1-p)^{1}\left({\frac {0}{p}}-{\frac {1}{1-p}}\right)^{2} }}\\&={\frac {1}{\sqrt {p(1-p)}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/324e2e5a963eed1652cf2d3a9ba95e5491b5df95)







![{\displaystyle {\begin{aligned}&{\text{апостериорная плотность вероятности}}(x=p\mid s,ns)\\[6pt]={}&{\frac {\operatorname {priorprobabilitydensity} (x= p;\alpha \operatorname {prior} ,\beta \operatorname {prior} ){\mathcal {L}}(s,f\mid x=p)}{\int _{0}^{1}{\text {априорная плотность вероятности}}(x=p;\alpha \operatorname {prior} ,\beta \operatorname {prior} ){\mathcal {L}}(s,f\mid x=p)\,dx}}\ \[6pt]={}&{\frac {{n \choose s}x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} - 1}/\mathrm {B} (\alpha \operatorname {prior} ,\beta \operatorname {prior} )}{\int _{0}^{1}\left({n \choose s}x^{s+ \alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}/\mathrm {B} (\alpha \operatorname {prior} ,\beta \operatorname { Prior} )\right)\,dx}}\\[6pt]={}&{\frac {x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}}{\int _{0}^{1}\left(x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \ имя оператора {prior} -1}\right)\,dx}}\\[6pt]={}&{\frac {x^{s+\alpha \operatorname {prior} -1}(1-x)^{n -s+\beta \operatorname {prior} -1}}{\mathrm {B} (s+\alpha \operatorname {prior} ,n-s+\beta \operatorname {prior} )}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/569ad0317cf545ff98538c8a845f216120e87c08)














![{\displaystyle {\begin{aligned}\mu (X)&={\frac {a+4b+c}{6}}\\[8pt]\sigma (X)&={\frac {ca}{6 }}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a89a68d1250ebe659be15e88edb5a9eb3e0cf87)



























