Коэффициент Джини

Не путать с примесью Джини .

Список стран, отсортированных по коэффициенту Джини, см. в разделе Список стран по коэффициенту Джини .

Карта неравенства доходов Коэффициенты Джини по странам (%). На основе данных Всемирного банка за период с 1992 по 2020 год.

•   Выше 50
•   Между 45 и 50
•   Между 40 и 45
•   Между 35 и 40
•   Между 30 и 35
•   Ниже 30
•   Нет данных

Другая карта, показывающая коэффициенты Джини богатства внутри стран на 2019 год.

Доля доходов 1% богатейших людей в отдельных развитых странах, 1975–2015 гг.

В экономике коэффициент Джини ( / ˈ dʒ iː n i / JEE -nee ), также известный как индекс Джини или коэффициент Джини , является мерой статистической дисперсии, предназначенной для представления неравенства доходов , неравенства богатства или неравенства потребления. внутри нации или социальной группы . Его разработал итальянский статистик и социолог Коррадо Джини .

Коэффициент Джини измеряет неравенство между значениями частотного распределения , такими как уровни дохода . Коэффициент Джини, равный 0, отражает идеальное равенство, при котором все значения дохода или богатства одинаковы, тогда как коэффициент Джини, равный 1 (или 100%), отражает максимальное неравенство между ценностями, ситуацию, когда один человек имеет весь доход, в то время как все остальные имеют никто.

мера неравенства доходов Коэффициент Джини был предложен Коррадо Джини как или богатства . Для стран ОЭСР в конце 20-го века, учитывая влияние налогов и трансфертных платежей , коэффициент Джини дохода колебался от 0,24 до 0,49, при этом в Словакии был самый низкий показатель, а в Мексике - самый высокий. В 2008–2009 годах в африканских странах были самые высокие коэффициенты Джини до уплаты налогов, при этом в Южной Африке был самый высокий в мире коэффициент, который оценивался от 0,63 до 0,7. Однако этот показатель падает до 0,52 после учета социальной помощи и снова падает до 0,47 после налогообложения. Страной с самым низким коэффициентом Джини является Словакия с коэффициентом Джини 0,232. Коэффициент Джини мирового дохода в 2005 году, по оценкам различных источников, составлял от 0,61 до 0,68.

Существуют некоторые проблемы с интерпретацией коэффициента Джини, поскольку одно и то же значение может быть получено из множества разных кривых распределения. Чтобы смягчить это, следует принять во внимание демографическую структуру. В странах со стареющим населением или с повышенным уровнем рождаемости коэффициент Джини до уплаты налогов увеличивается, даже если реальное распределение доходов работающего взрослого населения остается постоянным. Многие ученые разработали более десятка вариантов коэффициента Джини.

История

Коэффициент Джини был разработан итальянским статистиком Коррадо Джини и опубликован в его статье 1912 года Variabilità e mutabilità (англ.: изменчивость и изменчивость ). Опираясь на работы американского экономиста Макса Лоренца , Джини предложил использовать в качестве меры неравенства разницу между гипотетической прямой линией, изображающей совершенное равенство, и фактической линией, изображающей доходы людей. В этой статье он ввел концепцию простой средней разности как меры изменчивости.

Затем он применил простую среднюю разницу наблюдаемых переменных к неравенству доходов и богатства в своей работе «Об измерении концентрации и изменчивости характеров» в 1914 году. Здесь он представил коэффициент концентрации , который получил дальнейшее развитие в коэффициенте Джини, используемом сегодня. Во-вторых, Джини заметил, что предложенное им соотношение также может быть достигнуто путем улучшения методов, уже предложенных Лоренцем, Шатленом или Сейем.

В 1915 году Гаэтано Пьетра представил геометрическую интерпретацию предложенного Джини соотношения и соотношения между площадью наблюдаемой концентрации и максимальной концентрацией. Эта измененная версия коэффициента Джини стала наиболее часто используемым индексом неравенства в последующие годы.

По данным ОЭСР , коэффициент Джини впервые был официально использован в масштабах всей страны в Канаде в 1970-х годах. Канадский индекс неравенства доходов колебался от 0,303 до 0,284 с 1976 года до конца 1980-х годов. ОЭСР начала публиковать данные большего количества стран с начала XXI века. ^ул. век. Страны Центральной Европы Словения , Чехия и Словакия имели самый низкий индекс неравенства среди всех стран ОЭСР с 2000-х годов. Скандинавские страны также часто оказывались на вершине списка равенства в последние десятилетия.

Определение

Коэффициент Джини равен площади, обозначенной буквой A, деленной на общую площадь A и B , т.е. ${\text{Gini}}={\tfrac {A}{A+B}}$. Оси идут от 0 до 1, поэтому A и B образуют треугольник площади. ${\tfrac {1}{2}}$ и ${\text{Gini}}=2A=1-2B$.

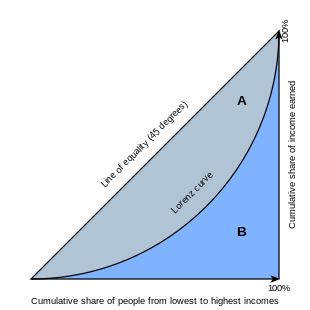
Коэффициент Джини — это индекс степени неравенства в распределении доходов/богатства, используемый для оценки того, насколько далеко богатство или распределение доходов в стране отклоняются от равного распределения.

Коэффициент Джини обычно определяется математически на основе кривой Лоренца , которая отображает долю общего дохода населения (ось Y), кумулятивно заработанную нижней частью x (см. Диаграмму). населения Таким образом, линия под углом 45 градусов представляет собой совершенное равенство доходов. Тогда коэффициент Джини можно рассматривать как отношение площади, лежащей между линией равенства и кривой Лоренца (отмеченной на диаграмме буквой A ), к общей площади под линией равенства (отмеченной A и B на диаграмме буквой ). ; т. е. G = A /( A + B ) . Если отрицательных доходов нет, то он также равен 2 A и 1 − 2 B в силу того, что A + B = 0,5 .

Предполагая неотрицательный доход или богатство для всех, теоретический диапазон коэффициента Джини составляет от 0 (полное равенство) до 1 (абсолютное неравенство). Этот показатель часто выражается в процентах от 0 до 100. Однако если учитывать отрицательные значения, как в случае долга, индекс Джини может превысить 1. Обычно мы предполагаем положительное среднее или общее значение, исключая коэффициент Джини. ниже нуля.

Альтернативный подход заключается в определении коэффициента Джини как половины относительной средней абсолютной разницы , что эквивалентно определению, основанному на кривой Лоренца . Средняя абсолютная разница — это средняя абсолютная разница всех пар элементов генеральной совокупности, а относительная средняя абсолютная разница — это средняя абсолютная разница, деленная на среднее значение . ${\bar {x}}$, чтобы нормализовать масштаб. Если x _i — это богатство или доход человека i и имеется n человек, то коэффициент Джини G определяется по формуле:

$G={\frac {\displaystyle {\sum _{i=1}^{n}\sum _{j=1}^{n}\left|x_{i}-x_{j}\right|}}{\displaystyle {2\sum _{i=1}^{n}\sum _{j=1}^{n}x_{j}}}}={\frac {\displaystyle {\sum _{i=1}^{n}\sum _{j=1}^{n}\left|x_{i}-x_{j}\right|}}{\displaystyle {2n\sum _{j=1}^{n}x_{j}}}}={\frac {\displaystyle {\sum _{i=1}^{n}\sum _{j=1}^{n}\left|x_{i}-x_{j}\right|}}{\displaystyle {2n^{2}{\bar {x}}}}}$

Когда распределение дохода (или богатства) задается как непрерывная функция плотности вероятности p ( x ), коэффициент Джини снова составляет половину относительной средней абсолютной разницы:

$G={\frac {1}{2\mu }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }p(x)p(y)\,|x-y|\,dx\,dy$

где $\textstyle \mu =\int _{-\infty }^{\infty }xp(x)\,dx$ является средним значением распределения, а нижние пределы интегрирования могут быть заменены нулем, когда все доходы положительны.

Расчет

Самая богатая часть населения (красный) имеет равную долю f от всех доходов или богатства; другие (зеленые) делят остаток поровну: G = f - u . Гладкое распределение (синее) с одинаковыми u и f всегда имеет G > f − u .

Неравенство благосостояния в крупных городах

Палатки бездомных на тротуаре в Скид-Роу, Лос-Анджелес.

Богатый дом в Холмби-Хиллз, Лос-Анджелес , примерно в 12 милях от центра города (вверху)

Хотя распределение доходов в любой конкретной стране не будет полностью соответствовать теоретическим моделям , эти модели могут дать качественное объяснение распределения доходов в стране с учетом коэффициента Джини.

Пример: Два уровня дохода

Крайние случаи представлены максимально равным обществом, в котором каждый человек получает одинаковый доход ( G = 0 ), и наиболее неравным обществом (с N индивидами), где один человек получает 100% общего дохода, а остальные N − 1 человек не получает ни одного ( G = 1 − 1/ N ).

Простой случай предполагает всего два уровня дохода: низкий и высокий. Если группа с высоким доходом составляет долю u населения и зарабатывает долю f от всех доходов, то коэффициент Джини равен f − u . Более градуированное распределение с теми же значениями u и f всегда будет иметь более высокий коэффициент Джини, чем f − u .

Например, если самые богатые u = 20% населения имеют f = 80% всех доходов (см. принцип Парето ), коэффициент Джини дохода составляет не менее 60%. В другом примере если u = 1% населения мира владеет f = 50% всего богатства, коэффициент Джини богатства составляет не менее 49%.

Альтернативные выражения

В некоторых случаях это уравнение можно применить для расчета коэффициента Джини без прямой ссылки на кривую Лоренца . Например (где y обозначает доход или богатство человека или домохозяйства):

• Для популяции из n особей со значениями $y_{1}\leq y_{2}\leq \cdots \leq y_{n}$,

$G={\frac {1}{n}}\left(n+1-2\left({\frac {\sum _{i=1}^{n}(n+1-i)y_{i}}{\sum _{i=1}^{n}y_{i}}}\right)\right).$

Это можно упростить до:

$G={\frac {2\sum _{i=1}^{n}iy_{i}}{n\sum _{i=1}^{n}y_{i}}}-{\frac {n+1}{n}}.$

Коэффициент Джини также можно рассматривать как половину относительной средней абсолютной разницы . Для случайной выборки S со значениями $y_{1}\leq y_{2}\leq \cdots \leq y_{n}$, выборочный коэффициент Джини

$G(S)={\frac {1}{n-1}}\left(n+1-2\left({\frac {\sum _{i=1}^{n}(n+1-i)y_{i}}{\sum _{i=1}^{n}y_{i}}}\right)\right)$

является последовательной оценкой коэффициента Джини населения, но в целом не является беспристрастным . В упрощенной форме:

$G(S)=1-{\frac {2}{n-1}}\left(n-{\frac {\sum _{i=1}^{n}iy_{i}}{\sum _{i=1}^{n}y_{i}}}\right).$

Не существует выборочной статистики, которая всегда давала бы несмещенную оценку коэффициента Джини населения.

вероятностей

Для дискретного распределения вероятностей с функцией вероятностной массы $f(y_{i}),$ $i=1,\ldots ,n$, где $f(y_{i})$ это доля населения с доходом или богатством $y_{i}>0$, коэффициент Джини равен:

$G={\frac {1}{2\mu }}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\,f(y_{i})f(y_{j})|y_{i}-y_{j}|$

где

$\mu =\sum \limits _{i=1}^{n}y_{i}f(y_{i}).$

Если точки с ненулевыми вероятностями пронумерованы в порядке возрастания $(y_{i}<y_{i+1})$, затем:

$G=1-{\frac {\sum _{i=1}^{n}f(y_{i})(S_{i-1}+S_{i})}{S_{n}}}$

где

$S_{i}=\sum _{j=1}^{i}f(y_{j})\,y_{j}\,$ и $S_{0}=0.$ Эти формулы применимы и в пределе, т.к. $n\rightarrow \infty .$

вероятностей

Когда население велико, распределение доходов может быть представлено непрерывной функцией плотности вероятности f ( x ), где f ( x ) dx — это доля населения с богатством или доходом в интервале dx вокруг x . Если F ( x ) — кумулятивная функция распределения для f ( x ):

$F(x)=\int _{0}^{x}f(x)\,dx$

и L ( x ) — функция Лоренца:

$L(x)={\frac {\int _{0}^{x}x\,f(x)\,dx}{\int _{0}^{\infty }x\,f(x)\,dx}}$

тогда кривая Лоренца L ( F ) может быть представлена ​​как функция, параметрическая относительно L ( x ) и F ( x ), а значение B можно найти путем интегрирования :

$B=\int _{0}^{1}L(F)\,dF.$

Коэффициент Джини также можно рассчитать непосредственно из кумулятивной функции распределения распределения F ( y ). Определив μ как среднее значение распределения и указав, что F ( y ) равно нулю для всех отрицательных значений, коэффициент Джини определяется как:

$G=1-{\frac {1}{\mu }}\int _{0}^{\infty }(1-F(y))^{2}\,dy={\frac {1}{\mu }}\int _{0}^{\infty }F(y)(1-F(y))\,dy$

Последний результат получается в результате интегрирования по частям . (Обратите внимание, что эту формулу можно применять, когда имеются отрицательные значения, если интегрирование производится от минус бесконечности до плюс бесконечности.)

Коэффициент Джини может быть выражен через функцию квантиля Q ( F ) (обратную кумулятивной функции распределения: Q (F (x)) = x)

$G={\frac {1}{2\mu }}\int _{0}^{1}\int _{0}^{1}|Q(F_{1})-Q(F_{2})|\,dF_{1}\,dF_{2}.$

Поскольку коэффициент Джини не зависит от масштаба , если функцию распределения можно выразить в форме f(x,φ,a,b,c...) , где φ — масштабный коэффициент, а , b, c... a безразмерных параметров, то коэффициент Джини будет функцией только a, b, c... . Например, для экспоненциального распределения , которое является функцией только x и параметра масштаба, коэффициент Джини является константой, равной 1/2.

Для некоторых функциональных форм индекс Джини можно рассчитать явно. Например, если y соответствует логнормальному распределению со стандартным отклонением журналов, равным $\sigma$, затем $G=\operatorname {erf} \left({\frac {\sigma }{2}}\right)$ где $\operatorname {erf}$ – функция ошибки (поскольку $G=2\Phi \left({\frac {\sigma }{\sqrt {2}}}\right)-1$, где $\Phi$ — кумулятивная функция распределения стандартного нормального распределения). В таблице ниже приведены некоторые примеры функций плотности вероятности с поддержкой $[0,\infty )$ показаны. Дельта-распределение Дирака представляет собой случай, когда все имеют одинаковое богатство (или доход); это подразумевает отсутствие различий между доходами.

Функция распределения доходов	PDF(х)	Коэффициент Джини
Дельта-функция Дирака	$\delta (x-x_{0}),\,x_{0}>0$	0
Равномерное распределение	${\begin{cases}{\frac {1}{b-a}}&a\leq x\leq b\\0&\mathrm {otherwise} \end{cases}}$	${\frac {(b-a)}{3(b+a)}}$
Экспоненциальное распределение	$\lambda e^{-x\lambda },\,\,x>0$	$1/2$
Логнормальное распределение	${\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {\ln \,(x)-\mu }{\sigma }}\right)^{2}}$	${\textrm {erf}}(\sigma /2)=2\Phi \left({\frac {\sigma }{\sqrt {2}}}\right)-1$
Распределение Парето	${\begin{cases}{\frac {\alpha k^{\alpha }}{x^{\alpha +1}}}&x\geq k\\0&x<k\end{cases}}$	${\begin{cases}1&0<\alpha <1\\{\frac {1}{2\alpha -1}}&\alpha \geq 1\end{cases}}$
Распределение ци	$f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geq 0\\0,&x<0\end{cases}}$	$(-1)^{k}\left|I_{-1}(k,{\tfrac {1}{2}})\right|$
Распределение хи-квадрат	${\frac {2^{-k/2}e^{-x/2}x^{k/2-1}}{\Gamma (k/2)}}$	${\frac {2\,\Gamma \left({\frac {1+k}{2}}\right)}{k\,\Gamma (k/2){\sqrt {\pi }}}}$
Гамма-распределение	${\frac {e^{-x/\theta }x^{k-1}\theta ^{-k}}{\Gamma (k)}}$	${\frac {\Gamma \left({\frac {2k+1}{2}}\right)}{k\,\Gamma (k){\sqrt {\pi }}}}$
Распределение Вейбулла	${\frac {k}{\lambda }}\,\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}$	$1-2^{-1/k}$
Бета-дистрибутив	${\frac {x^{\alpha -1}(1-x)^{\beta -1}}{B(\alpha ,\beta )}}$	$\left({\frac {2}{\alpha }}\right){\frac {B(\alpha +\beta ,\alpha +\beta )}{B(\alpha ,\alpha )B(\beta ,\beta )}}$
Лог-логистическая дистрибуция	${\frac {(\beta /\alpha )(x/\alpha )^{\beta -1}}{\left(1+(x/\alpha )^{\beta }\right)^{2}}}$	$1/\beta$

• $\Gamma (\,)$ это гамма-функция
• $B(\,)$ это бета-функция
• $I_{k}(\,)$ - регуляризованная неполная бета-функция

Другие подходы

Иногда вся кривая Лоренца неизвестна, и приводятся только значения через определенные интервалы. В этом случае коэффициент Джини можно аппроксимировать, используя различные методы интерполяции недостающих значений кривой Лоренца. Если ( X _k , Y _k ) — известные точки на кривой Лоренца, причем X _k пронумерованы в порядке возрастания ( X _{k – 1} < X _k ), так что:

• X _k — накопленная доля переменной совокупности для k = 0,..., n , с X ₀ = 0, X _n = 1.
• Y _k — накопленная доля переменной дохода для k = 0,..., n , с Y ₀ = 0, Y _n = 1.
• Y _k должен быть пронумерован в порядке неубывания ( Y _k > Y _{k – 1} )

Если кривую Лоренца аппроксимировать на каждом интервале линией между последовательными точками, то область B можно аппроксимировать трапециями и:

$G_{1}=1-\sum _{k=1}^{n}(X_{k}-X_{k-1})(Y_{k}+Y_{k-1})$

является результирующей аппроксимацией для G. Более точные результаты можно получить, используя другие методы аппроксимации области B, такие как аппроксимация кривой Лоренца квадратичной функцией по парам интервалов или построение достаточно гладкой аппроксимации базовой функции распределения, которая соответствует известные данные. Если также известны среднее значение генеральной совокупности и граничные значения для каждого интервала, их также часто можно использовать для повышения точности аппроксимации.

Коэффициент Джини, рассчитанный на основе выборки, является статистическим показателем, и следует указать его стандартную ошибку или доверительные интервалы для коэффициента Джини генеральной совокупности. Их можно рассчитать с помощью методов начальной загрузки , математически сложных и требовательных к вычислениям даже в эпоху быстрых компьютеров. Экономист Томсон Огванг сделал этот процесс более эффективным, создав «хитрую регрессионную модель», в которой соответствующие переменные дохода в выборке ранжируются, при этом самому низкому доходу присваивается ранг 1. Затем модель выражает ранг (зависимую переменную) как сумму константы A и нормальной ошибки, дисперсия которой обратно пропорциональна y _k :

$k=A+\ N(0,s^{2}/y_{k})$

Таким образом, G можно выразить как функцию взвешенной методом наименьших квадратов оценки константы A , и это можно использовать для ускорения расчета оценки складным ножом стандартной ошибки . Экономист Дэвид Джайлс утверждал, что стандартная ошибка оценки A может быть использована для получения оценки G напрямую, без использования складного ножа. Этот метод требует использования обычной регрессии наименьших квадратов только после упорядочивания выборочных данных. Результаты выгодно отличаются от оценок, полученных с помощью складного ножа , причем согласие улучшается с увеличением размера выборки.

Однако утверждалось, что это зависит от допущений модели о распределении ошибок и независимости членов ошибок. Эти предположения часто не справедливы для реальных наборов данных. Вокруг этой темы до сих пор продолжаются споры.

Гильермина Яссо и Ангус Дитон независимо предложил следующую формулу для коэффициента Джини:

$G={\frac {N+1}{N-1}}-{\frac {2}{N(N-1)\mu }}(\sum _{i=1}^{n}P_{i}X_{i})$

где $\mu$ — средний доход населения, P _i самый богатый человек получает ранг 1, а самый бедный — ранг N. — ранг дохода P человека i с доходом X, так что Это фактически придает больший вес более бедным людям в распределении доходов, что позволяет коэффициенту Джини соответствовать принципу трансферта . Обратите внимание, что формула Яссо-Дитона изменяет масштаб коэффициента так, что его значение равно единице, если все $X_{i}$ равны нулю, кроме единицы. Однако обратите внимание на ответ Эллисона о необходимости вместо этого разделить на N².

ФАО объясняет другую версию формулы.

неравенства

См. Также: Обобщенный индекс энтропии.

Коэффициент Джини и другие стандартные индексы неравенства приводятся к общему виду. Совершенное равенство – отсутствие неравенства – существует тогда и только тогда, когда соотношение неравенства $r_{j}=x_{j}/{\overline {x}}$, равен 1 для всех j единиц в некоторой популяции (например, существует полное равенство доходов, когда доход каждого $x_{j}$ равен среднему доходу ${\overline {x}}$, так что $r_{j}=1$ для всех). Таким образом, мерами неравенства являются меры средних отклонений $r_{j}=1$ от 1; чем больше среднее отклонение, тем больше неравенство. На основе этих наблюдений индексы неравенства имеют следующую общую форму:

${\text{Inequality}}=\sum _{j}p_{j}\,f(r_{j}),$

где p _j взвешивает единицы по их доле в численности населения, а f ( r _j ) является функцией отклонения r _j каждой единицы от 1, точки равенства. Суть этого обобщенного индекса неравенства заключается в том, что индексы неравенства различаются, поскольку они используют разные функции расстояния между коэффициентами неравенства ( ) _rj от 1.

О

Смотрите также: Список стран по равенству доходов

Вывод кривой Лоренца и коэффициента Джини для мирового дохода в 2011 г.

. .

Коэффициенты дохода Джини рассчитываются на основе рыночного дохода и располагаемого дохода. Коэффициент Джини для рыночного дохода, иногда называемый коэффициентом Джини до уплаты налогов, рассчитывается на основе дохода до уплаты налогов и трансфертов. Он измеряет неравенство в доходах без учета влияния налогов и социальных расходов, уже существующих в стране. Коэффициент Джини располагаемого дохода, иногда называемый коэффициентом Джини после уплаты налогов, рассчитывается на основе дохода после уплаты налогов и трансфертов. Он измеряет неравенство в доходах после рассмотрения влияния налогов и социальных расходов, уже существующих в стране.

Для стран ОЭСР в период 2008–2009 годов коэффициент Джини (до уплаты налогов и трансфертов) для общей численности населения колебался от 0,34 до 0,53, при этом в Южной Корее самый низкий показатель, а в Италии — самый высокий. Коэффициент Джини (после уплаты налогов и трансфертов) для всего населения колебался от 0,25 до 0,48, при этом самый низкий коэффициент был в Дании, а самый высокий в Мексике. Для Соединенных Штатов, страны с самой большой численностью населения среди стран ОЭСР, индекс Джини до уплаты налогов составлял 0,49, а индекс Джини после уплаты налогов составлял 0,38 в 2008–2009 годах. Средний показатель по ОЭСР для всего населения в странах ОЭСР составил 0,46 для индекса Джини дохода до уплаты налогов и 0,31 для индекса Джини дохода после уплаты налогов. Налоги и социальные расходы, которые действовали в период 2008–2009 годов в странах ОЭСР, значительно снизили эффективное неравенство доходов, и в целом «европейские страны, особенно скандинавские и континентальные государства всеобщего благосостояния , достигают более низкого уровня неравенства доходов, чем другие страны».

Использование индекса Джини может помочь количественно оценить различия в социального обеспечения и компенсаций политике и философии . Однако следует иметь в виду, что коэффициент Джини может вводить в заблуждение, когда он используется для политических сравнений между большими и малыми странами или странами с различной иммиграционной политикой (см. раздел «Ограничения »).

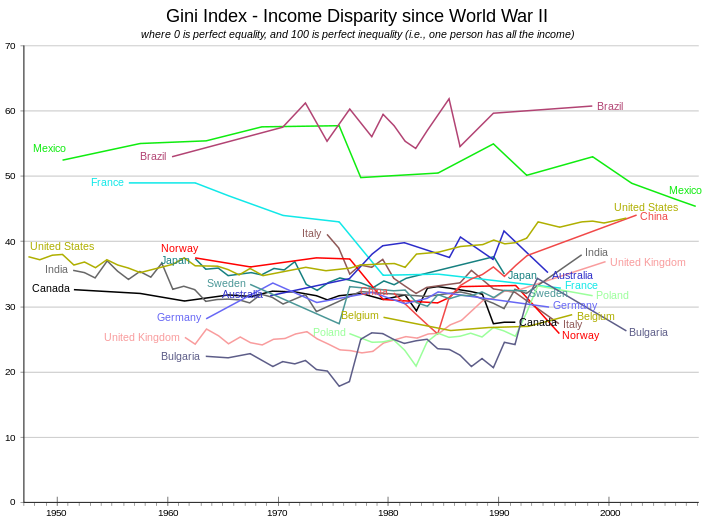
Коэффициент Джини для всего мира, по оценкам различных сторон, составляет от 0,61 до 0,68. На графике показаны значения, выраженные в процентах от их исторического развития для ряда стран.

доходов

По данным ЮНИСЕФ, в Латинской Америке и Карибском регионе был самый высокий индекс Джини чистого дохода в мире - 48,3 на невзвешенной средней основе в 2008 году. Остальными средними показателями по регионам были: Африка к югу от Сахары (44,2), Азия (40,4), Ближний Восток и Северная Африка (39,2), Восточная Европа и Центральная Азия (35,4) и страны с высоким уровнем дохода (30,9). Используя тот же метод, утверждается, что в Соединенных Штатах индекс Джини равен 36, в то время как в Южной Африке самый высокий показатель индекса Джини доходов составляет 67,8.

Индекс Джини мирового дохода с 1800

Если принять во внимание распределение доходов всех людей, то неравенство доходов во всем мире постоянно растет с начала 19 века (и будет продолжать увеличиваться с годами). В период с 1820 по 2002 год наблюдался устойчивый рост глобального неравенства доходов по шкале Джини, причем значительный рост наблюдался в период с 1980 по 2002 год. Эта тенденция, похоже, достигла своего пика и начала разворот с быстрым экономическим ростом в странах с развивающейся экономикой, особенно в больших группах населения Страны БРИК .

В таблице ниже представлены расчетные коэффициенты Джини мирового дохода за последние 200 лет, рассчитанные Милановичем.

Коэффициент Джини дохода - мир, 1820–2005 гг.

Год	Мировые коэффициенты Джини
1820	0.43
1850	0.53
1870	0.56
1913	0.61
1929	0.62
1950	0.64
1960	0.64
1980	0.66
2002	0.71
2005	0.68

Более подробные данные из аналогичных источников показывают непрерывное снижение с 1988 года. Это объясняется глобализацией, увеличивающей доходы миллиардов бедных людей, в основном в таких странах, как Китай и Индия. Развивающиеся страны, такие как Бразилия, также улучшили базовые услуги, такие как здравоохранение, образование и санитария; другие, такие как Чили и Мексика, ввели более прогрессивную налоговую политику.

Коэффициент Джини дохода – мир, 1988–2013 гг.

Год	Мировые коэффициенты Джини
1988	0.80
1993	0.76
1998	0.74
2003	0.72
2008	0.70
2013	0.65

Социального развития

Коэффициент Джини широко используется в таких разнообразных областях, как социология, экономика, здравоохранение, экология, инженерия и сельское хозяйство. Например, в социальных науках и экономике, помимо коэффициентов Джини доходов, ученые опубликовали коэффициенты Джини образования и коэффициенты Джини возможностей.

Образование

Индекс Джини в сфере образования оценивает неравенство в образовании для данного населения. Он используется для выявления тенденций в социальном развитии через уровень образования с течением времени. Исследование, проведенное тремя экономистами Всемирного банка , Винодом Томасом, Яном Вангом и Сибо Фаном, в 85 странах показало, что в 1990 году в Мали был самый высокий индекс Джини в области образования, равный 0,92 (что подразумевает очень высокое неравенство в уровне образования среди населения), в то время как в Соединенных Штатах имел самый низкий индекс неравенства в образовании Джини - 0,14. В период с 1960 по 1990 годы в Китае, Индии и Южной Корее наблюдалось самое быстрое снижение индекса Джини неравенства в образовании. Они также утверждают, что индекс Джини в сфере образования в Соединенных Штатах немного увеличился за период 1980–1990 годов.

Хотя индекс Джини в области образования в Индии падал с 1960 по 1990 годы, большая часть населения до сих пор не получила никакого образования, в то время как 10 процентов населения получили более 40% общего количества образовательных часов в стране. Это означает, что значительная часть способных детей в стране не получает поддержки, необходимой для того, чтобы они могли внести позитивный вклад в жизнь общества. Это приведет к безвозвратным потерям для национального общества, поскольку многие люди недостаточно развиты и недостаточно задействованы.

Возможность

По своей концепции аналогичный коэффициенту дохода Джини, коэффициент возможностей Джини измеряет неравенство в возможностях. Концепция основана на Амартии Сена. предложении что коэффициенты неравенства социального развития должны основываться на процессе расширения выбора людей и повышения их возможностей, а не на процессе сокращения неравенства доходов. Ковачевич в обзоре коэффициента возможностей Джини объяснил, что этот коэффициент оценивает, насколько хорошо общество позволяет своим гражданам добиваться успеха в жизни, где успех основан на выборе, усилиях и талантах человека, а не на его опыте, определяемом набором заранее определенные обстоятельства при рождении, такие как пол, раса, место рождения, доход родителя и обстоятельства, не зависящие от этого человека.

В 2003 году Ремер Сообщается, что Италия и Испания продемонстрировали самый большой индекс Джини неравенства возможностей среди стран с развитой экономикой.

дохода

В 1978 году Энтони Шоррокс представил показатель, основанный на коэффициентах Джини дохода, для оценки мобильности доходов. Эта мера, обобщенная Маасуми и Зандвакили, теперь обычно называют индексом Шоррокса , иногда индексом подвижности Шоррокса или индексом жесткости Шоррокса. Он пытается оценить, является ли коэффициент неравенства доходов Джини постоянным или временным, и в какой степени страна или регион обеспечивает экономическую мобильность своему народу, чтобы они могли перейти из одного квантиля доходов (например, 20% нижних слоев населения) в другой (например, средний уровень дохода). 20%) с течением времени. Другими словами, индекс Шоррокса сравнивает неравенство краткосрочных доходов, таких как годовой доход домохозяйств, с неравенством долгосрочных доходов, таких как общий доход за 5 или 10 лет для тех же домохозяйств.

Индекс Шоррокса рассчитывается несколькими различными способами, общий подход заключается в соотношении коэффициентов Джини доходов между краткосрочными и долгосрочными доходами для одного и того же региона или страны.

Исследование 2010 года с использованием данных о доходах на социальное обеспечение в Соединенных Штатах с 1937 года и индексов Шоррока на основе Джини пришло к выводу, что мобильность доходов в Соединенных Штатах имеет сложную историю, в первую очередь из-за массового притока женщин в американскую рабочую силу после мировой войны. II. Тенденции неравенства доходов и мобильности доходов были разными для мужчин и женщин в период с 1937 по 2000-е годы. Если рассматривать мужчин и женщин вместе, тенденции индекса Шоррокса, основанного на коэффициенте Джини, подразумевают, что долгосрочное неравенство доходов существенно сократилось среди всех работников в последние десятилетия в Соединенных Штатах. Другие ученые, используя данные только 1990-х годов или других коротких периодов, пришли к другим выводам. Например, Састре и Айала на основе своего исследования данных коэффициента Джини доходов в период с 1993 по 1998 год для шести развитых стран пришли к выводу, что Франция имела наименьшую мобильность доходов, Италия - самый высокий, а США и Германия - промежуточные уровни мобильности доходов за эти пять лет. .

Особенности

Коэффициент Джини имеет особенности, которые делают его полезным в качестве меры дисперсии населения и, в частности, неравенства. Коэффициент варьируется от 0 (полное равенство) до 1 (полное неравенство). Джини основан на сравнении совокупной доли населения с совокупной долей доходов, которые оно получает.

Ограничения

Коэффициент Джини является относительной мерой. Коэффициент Джини развивающейся страны может повыситься (из-за растущего неравенства доходов) даже тогда, когда число людей, живущих в абсолютной бедности, уменьшается. Это связано с тем, что коэффициент Джини измеряет относительное, а не абсолютное богатство. Изменение неравенства доходов, измеряемое коэффициентами Джини, может быть связано со структурными изменениями в обществе, такими как рост населения (повышение рождаемости, старение населения, увеличение количества разводов, расширенных семей разделение домохозяйств на нуклеарные семьи , эмиграция, иммиграция) и мобильность доходов. Коэффициенты Джини просты, и эта простота может привести к упущениям и затруднить сравнение различных групп населения; например, хотя и в Бангладеш (доход на душу населения 1693 доллара США), и в Нидерландах (доход на душу населения 42 183 доллара США) коэффициент Джини дохода в 2010 году составлял 0,31, качество жизни, экономические возможности и абсолютный доход в этих странах очень различаются, т.е. страны могут иметь одинаковые коэффициенты Джини, но сильно различаться по уровню благосостояния. В развитой экономике предметы первой необходимости могут быть доступны всем, в то время как в неразвитой экономике с тем же коэффициентом Джини предметы первой необходимости могут быть недоступны большинству или доступны не в равной степени из-за более низкого абсолютного богатства.

Таблица А. Различные распределения доходов при одном и том же индексе Джини

Группа домохозяйств	Страна Годовой доход ($)	Годовой доход страны Б ($)
1	20,000	9,000
2	30,000	40,000
3	40,000	48,000
4	50,000	48,000
5	60,000	55,000
Общий доход	$200,000	$200,000
Джини страны	0.2	0.2

Различные распределения доходов при одном и том же коэффициенте Джини

Даже если общий доход населения одинаков, в определенных ситуациях две страны с разным распределением доходов могут иметь один и тот же индекс Джини (например, случаи, когда кривые Лоренца дохода пересекаются). Таблица А иллюстрирует одну из таких ситуаций. В обеих странах коэффициент Джини равен 0,2, но среднее распределение доходов по группам домохозяйств различно. Другой пример: в популяции, где самые низкие 50% людей не имеют дохода, а остальные 50% имеют равный доход, коэффициент Джини равен 0,5; тогда как для другой группы населения, где 75% людей с самым низким доходом имеют 25% дохода, а 25% самых богатых людей имеют 75% дохода, индекс Джини также равен 0,5. Страны с одинаковыми доходами и коэффициентами Джини могут иметь очень разное распределение доходов. Беллу и Либерати утверждают, что ранжирование неравенства доходов между двумя группами населения не всегда возможно на основе их индексов Джини. Аналогичным образом, специалист по вычислительной социологии Фабиан Стефани показывает, что неравенство доходов внутри населения, например, в определенных социально-экономических группах одного возраста и образования, также остается незамеченным традиционными индексами Джини.

Крайнее неравенство богатства при низком коэффициенте Джини доходов

Индекс Джини не содержит информации об абсолютных национальных или личных доходах. Население может одновременно иметь индексы Джини с очень низким доходом и индексом Джини с очень высоким уровнем благосостояния. Измеряя неравенство в доходах, индекс Джини игнорирует дифференциальную эффективность использования доходов домохозяйств. Игнорируя богатство (за исключением случаев, когда оно способствует увеличению дохода), коэффициент Джини может создать видимость неравенства, когда сравниваемые люди находятся на разных этапах своей жизни. Богатые страны, такие как Швеция, могут демонстрировать низкий коэффициент Джини для располагаемого дохода, равный 0,31, тем самым казаясь равными, но при этом иметь очень высокий коэффициент Джини для богатства, составляющий от 0,79 до 0,86, что предполагает крайне неравномерное распределение богатства в их обществе. Эти факторы не оцениваются в индексе Джини, основанном на доходе.

Таблица B. Одинаковые распределения доходов, но разный индекс Джини

Номер домохозяйства	Годовой доход страны ($)	Бытовой комбинированный номер	Страна A Совокупный годовой доход ($)
1	20,000	1 и 2	50,000
2	30,000
3	40,000	3 и 4	90,000
4	50,000
5	60,000	5 и 6	130,000
6	70,000
7	80,000	7 и 8	170,000
8	90,000
9	120,000	9 и 10	270,000
10	150,000
Общий доход	$710,000		$710,000
Джини страны	0.303		0.293

Небольшая погрешность выборки – малонаселенные регионы с большей вероятностью будут иметь низкий коэффициент Джини.

Индекс Джини имеет тенденцию к снижению для небольших групп населения. Округа, штаты или страны с небольшим населением и менее разнообразной экономикой, как правило, сообщают о небольших коэффициентах Джини. Для экономически разнообразных больших групп населения ожидается гораздо более высокий коэффициент, чем для каждого из входящих в него регионов. Например, принимая во внимание мировую экономику в целом и распределение доходов среди всех людей, разные ученые оценивают глобальный индекс Джини в диапазоне от 0,61 до 0,68. Как и в случае с другими коэффициентами неравенства, на коэффициент Джини влияет степень детализации измерений. Например, пять 20%-ных квантилей (низкая степень детализации) обычно дают более низкий коэффициент Джини, чем двадцать 5%-ных квантилей (высокая степень детализации) для того же распределения. Филипп Монфор показал, что использование непоследовательной или неопределенной детализации ограничивает полезность измерений коэффициента Джини.

Коэффициент Джини дает разные результаты при применении к отдельным лицам, а не к домохозяйствам, для одной и той же экономики и одинакового распределения доходов. Если используются данные о домохозяйствах, измеренное значение дохода Джини зависит от того, как определяется домохозяйство. Сравнение не имеет смысла, если различные группы населения не оцениваются с помощью последовательных определений.

Дейнингер и Сквайр (1996) показывают, что коэффициент Джини дохода, основанный на индивидуальном доходе, а не на доходе домохозяйства, различен. Например, в США они обнаружили, что индекс Джини, основанный на индивидуальном доходе, составляет 0,35, а во Франции — 0,43. Согласно их индивидуально-ориентированному методу, в 108 странах, которые они изучали, Южная Африка имела самый высокий в мире коэффициент Джини - 0,62, Малайзия имела самый высокий коэффициент Джини в Азии - 0,5, Бразилия - самый высокий коэффициент Джини 0,57 в Латинской Америке и Карибском регионе, а также Турция. самый высокий показатель – 0,5 – в странах ОЭСР.

Таблица C. Распределение денежных доходов домохозяйств и индекс Джини, США

Группа доходов (в скорректированных долларах 2010 г.)	% населения 1979 г.	% населения 2010 г.
Менее 15 000 долларов США	14.6%	13.7%
$15,000 – $24,999	11.9%	12.0%
$25,000 – $34,999	12.1%	10.9%
$35,000 – $49,999	15.4%	13.9%
$50,000 – $74,999	22.1%	17.7%
$75,000 – $99,999	12.4%	11.4%
$100,000 – $149,999	8.3%	12.1%
$150,000 – $199,999	2.0%	4.5%
200 000 долларов и больше	1.2%	3.9%
Всего домохозяйств	80,776,000	118,682,000
Джини США до уплаты налогов	0.404	0.469

Коэффициент Джини не способен распознать последствия структурных изменений в популяции.

Развивая важность показателей продолжительности жизни, коэффициент Джини как точечная оценка равенства в определенный момент времени игнорирует изменения дохода в течение жизни. Как правило, увеличение доли молодых или пожилых членов общества приводит к очевидным изменениям в равенстве просто потому, что люди, как правило, имеют более низкие доходы и богатство в молодости, чем в пожилом возрасте. Из-за этого такие факторы, как возрастное распределение населения и мобильность внутри классов дохода, могут создать видимость неравенства, когда его нет, принимая во внимание демографические эффекты. Таким образом, данная экономика может иметь более высокий коэффициент Джини в любой момент времени по сравнению с другой, в то время как коэффициент Джини, рассчитанный на основе дохода человека в течение жизни, ниже, чем в явно более равной (в данный момент времени) экономике. По сути, важно не только неравенство в каком-либо конкретном году, но и структура распределения во времени.

Миллиардер Томас Квок заявил, что коэффициент Джини доходов в Гонконге был высоким (0,434 в 2010 г.). ), отчасти из-за структурных изменений в его населении. За последние десятилетия в Гонконге наблюдается рост числа небольших домохозяйств, пожилых семей и пожилых людей, живущих в одиночестве. Совокупный доход теперь делится на большее количество домохозяйств. Многие пожилые люди живут в Гонконге отдельно от своих детей. Эти социальные изменения привели к существенным изменениям в распределении доходов домохозяйств. Коэффициент Джини по доходам, утверждает Квок, не учитывает этих структурных изменений в обществе. Распределение денежных доходов домохозяйств в США, представленное в Таблице C этого раздела, подтверждает, что эта проблема не ограничивается только Гонконгом. По данным Бюро переписи населения США, в период с 1979 по 2010 год население Соединенных Штатов претерпело структурные изменения в домохозяйствах в целом; доход для всех категорий доходов увеличился с поправкой на инфляцию, распределение доходов домохозяйств со временем сместилось в группы с более высокими доходами, а коэффициент Джини дохода увеличился.

Еще одним ограничением коэффициента Джини является то, что он не является надлежащим показателем эгалитаризма , поскольку он измеряет лишь разброс доходов. Например, предположим, что две одинаково эгалитарные страны проводят разную иммиграционную политику. В этом случае страна, принимающая более высокую долю малообеспеченных или бедных мигрантов, сообщит о более высоком коэффициенте Джини и, следовательно, может демонстрировать большее неравенство доходов.

Неспособность оценить выгоды и доходы от неформальной экономики влияет на точность коэффициента Джини

Некоторые страны распределяют выгоды, которые трудно оценить. Страны, которые предоставляют субсидируемое жилье, медицинское обслуживание, образование или другие подобные услуги, трудно оценить объективно, поскольку это зависит от качества и размера льгот. В отсутствие свободного рынка оценка этих трансфертов дохода как дохода домохозяйств является субъективной. Теоретическая модель коэффициента Джини ограничена принятием правильных или неправильных субъективных предположений.

В условиях натуральной и неформальной экономики люди могут иметь значительный доход не только в денежной форме, но и в других формах, например, за счет натурального хозяйства или бартера . Эти доходы, как правило, достаются сегменту населения, находящемуся за чертой бедности или очень бедному в странах с формирующейся и переходной экономикой, таких как страны Африки к югу от Сахары, Латинская Америка, Азия и Восточная Европа. На неформальную экономику приходится более половины глобальной занятости и до 90 процентов занятости в некоторых беднейших странах к югу от Сахары с высокими официальными коэффициентами неравенства Джини. Шнайдер и др. в своем исследовании 162 стран, проведенном в 2010 г., Отчеты о 31,2%, или около 20 триллионов долларов мирового ВВП , являются неофициальными. В развивающихся странах неформальная экономика преобладает среди всех слоев населения, за исключением более богатых городских слоев населения с высокими доходами. Даже в развитых странах от 8% (США) до 27% (Италия) ВВП каждой страны является неформальным. Получаемый в результате неофициальный доход преобладает в качестве источника средств к существованию для людей с самыми низкими доходами. Стоимость и распределение доходов от неформальной или теневой экономики трудно определить количественно, что затрудняет оценку истинных коэффициентов Джини доходов. Различные предположения и количественные оценки этих доходов дадут разные коэффициенты Джини.

У Джини также есть некоторые математические ограничения. Он не является аддитивным, и различные группы людей не могут быть усреднены для получения коэффициента Джини для всех людей в группах.

Альтернативы

Учитывая ограничения коэффициента Джини, другие статистические методы используются в сочетании или в качестве альтернативной меры дисперсии населения. Например, меры энтропии часто используются (например, индекс Аткинсона или индекс Тейла и среднее логарифмическое отклонение как частные случаи обобщенного индекса энтропии ). Эти меры пытаются сравнить распределение ресурсов интеллектуальными агентами на рынке со максимальной энтропии случайным распределением , которое имело бы место, если бы эти агенты действовали как невзаимодействующие частицы в закрытой системе, следуя законам статистической физики.

с другими

Существует суммарная мера диагностической способности системы двоичного классификатора, которая также называется коэффициентом Джини , который определяется как удвоенная площадь между кривой рабочей характеристики приемника (ROC) и ее диагональю. Это связано с показателем производительности AUC ( площадь под кривой ROC), определяемым формулой $AUC=(G+1)/2$ и Манн-Уитни У. Хотя оба коэффициента Джини определяются как площади между определенными кривыми и обладают определенными свойствами, между коэффициентом статистической дисперсии Джини и коэффициентом Джини классификатора не существует простой прямой связи.

Индекс Джини также связан с индексом Пьетра, оба из которых измеряют статистическую неоднородность и выводятся из кривой Лоренца и диагональной линии.

В некоторых областях, таких как экология, обратный индекс Симпсона $1/\lambda$ используется для количественной оценки разнообразия, и его не следует путать с индексом Симпсона. $\lambda$. Эти показатели связаны с Джини. Обратный индекс Симпсона увеличивается с увеличением разнообразия, в отличие от индекса Симпсона и коэффициента Джини, которые уменьшаются с увеличением разнообразия. Индекс Симпсона находится в диапазоне [0, 1], где 0 означает максимальное разнообразие, а 1 — минимальное разнообразие (или гетерогенность). Поскольку индексы разнообразия обычно увеличиваются с увеличением неоднородности, индекс Симпсона часто преобразуется в обратный Симпсон или с использованием дополнения $1-\lambda$, известный как индекс Джини-Симпсона.

Кривая Лоренца — еще один метод графического представления распределения богатства. Он был разработан за 9 лет до появления коэффициента Джини, который количественно определяет степень отклонения кривой Лоренца от идеальной линии равенства (с наклоном 1). Индекс Гувера (также известный как индекс Робин Гуда) представляет собой процент совокупного дохода населения, который необходимо перераспределить, чтобы коэффициент Джини стал равным 0 (полное равенство).

досовременных обществ

В последние десятилетия исследователи пытались оценить коэффициенты Джини для обществ до 20-го века. В отсутствие обследований доходов домохозяйств и подоходного налога ученые полагались на косвенные переменные. К ним относятся налоги на богатство в средневековых европейских городах-государствах, модели землевладения в римском Египте , вариации размеров домов в обществах от древней Греции до ацтекской Мексики, а также наследование и приданое в вавилонском обществе. Другие данные не отражают напрямую изменений в богатстве или доходах, но, как известно, отражают неравенство, например, соотношение ренты к заработной плате или труда к капиталу.

Другое использование

Хотя коэффициент Джини наиболее популярен в экономике, теоретически его можно применять в любой области науки, изучающей распределение. Например, в экологии коэффициент Джини использовался как мера биоразнообразия , где совокупная доля видов отображается в зависимости от совокупной доли особей. В здравоохранении он использовался как мера неравенства качества жизни населения, связанного со здоровьем. В сфере образования он использовался как мера неравенства университетов. В химии его использовали для выражения селективности ингибиторов протеинкиназ в отношении ряда киназ. В технике он использовался для оценки справедливости, достигаемой интернет-маршрутизаторами при планировании передачи пакетов из различных потоков трафика.

Коэффициент Джини иногда используется для измерения дискриминационной силы рейтинговых систем при кредитным риском . управлении

В исследовании 2005 года были использованы данные переписи населения США для измерения владения домашними компьютерами и использован коэффициент Джини для измерения неравенства среди белых и афроамериканцев. Результаты показали, что, несмотря на общее снижение, неравенство в отношении владения домашними компьютерами было значительно меньше среди белых домохозяйств.

Рецензируемое исследование 2016 года под названием «Использование коэффициента Джини для измерения неравенства в участии в социальных сетях цифрового здравоохранения, ориентированных на лечение». продемонстрировал, что коэффициент Джини был полезен и точен при измерении изменений в неравенстве, однако в качестве отдельного показателя он не учитывал общий размер сети.

Дискриминационная сила относится к способности модели кредитного риска различать клиентов, не выполняющих свои обязательства, и клиентов, не выполняющих свои обязательства. Формула $G_{1}$, в разделе расчетов выше, может использоваться для окончательной модели и на уровне факторов отдельной модели для количественной оценки дискриминационной силы отдельных факторов. Это связано с коэффициентом точности в моделях оценки населения.

Коэффициент Джини также применялся для анализа неравенства в приложениях для знакомств .

Kaminskiy and Krivtsov распространил понятие коэффициента Джини из экономики на теорию надежности и предложил коэффициент типа Джини, который помогает оценить степень старения неремонтопригодных систем или старения и омоложения ремонтопригодных систем. Коэффициент определяется от -1 до 1 и может использоваться как в эмпирическом, так и в параметрическом распределении жизни. Он принимает отрицательные значения для класса распределений уменьшающейся интенсивности отказов и точечных процессов с уменьшающейся интенсивностью отказов и положителен для распределений возрастающей интенсивности отказов и точечных процессов с возрастающей интенсивностью отказов. Значение ноль соответствует экспоненциальному распределению жизни или однородному процессу Пуассона .

См. также

• Индекс разнообразия
• Экономическое неравенство
• Кривая Великого Гэтсби
• Индекс Херфиндаля-Хиршмана
• Индекс Гувера (он же индекс Робин Гуда)
• Индекс человеческой бедности
• Показатели неравенства доходов
• Кривая Кузнеца
• Список стран по равенству доходов
• Список стран по индексу человеческого развития с поправкой на неравенство
• Список стран по неравенству богатства
• Список штатов США по коэффициенту Джини
• Кривая Лоренца
• Эффект Мэтью
• Распределение Парето
• ROC-анализ
• Индекс костюмов
• Слоновья кривая
• утопия
• Благосостояние
• Экономика благосостояния

Дальнейшее чтение

• Амиэль, Ю.; Коуэлл, Ф.А. (1999). Думая о неравенстве . Кембридж. ISBN  978-0-521-46696-7 .
• Ананд, Судхир (1983). Неравенство и бедность в Малайзии . Нью-Йорк: Издательство Оксфордского университета. ISBN  978-0-19-520153-6 .
• Браун, Малькольм (1994). «Использование индексов в стиле Джини для оценки пространственных характеристик практикующих врачей: теоретические соображения и применение на основе данных Альберты». Социальные науки и медицина . 38 (9): 1243–1256. дои : 10.1016/0277-9536(94)90189-9 . ПМИД   8016689 .
• Чакраварти, SR (1990). Цифры этического социального индекса . Нью-Йорк: Springer-Verlag. ISBN  978-0-387-52274-6 .
• Дитон, Ангус (1997). Анализ обследований домохозяйств . Балтимор, Мэриленд: Издательство Университета Джонса Хопкинса. ISBN  978-0-585-23787-9 .
• Диксон, Филип М.; Вайнер, Джейкоб; Митчелл-Олдс, Томас; Вудли, Роберт (1987). «Создание коэффициента неравенства Джини». Экология . 68 (5): 1548–1551. дои : 10.2307/1939238 . JSTOR   1939238 . S2CID   84940050 .
• Дорфман, Роберт (1979). «Формула коэффициента Джини». Обзор экономики и статистики . 61 (1): 146–149. дои : 10.2307/1924845 . JSTOR   1924845 .
• Файербо, Гленн (2003). Новая география глобального неравенства доходов . Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN  978-0-674-01067-3 .
• Гаствирт, Джозеф Л. (1972). «Оценка кривой Лоренца и индекса Джини». Обзор экономики и статистики . 54 (3): 306–316. дои : 10.2307/1937992 . JSTOR   1937992 .
• Джайлз, Дэвид (2004). «Расчет стандартной ошибки для коэффициента Джини: некоторые дополнительные результаты» (PDF) . Оксфордский бюллетень экономики и статистики . 66 (3): 425–433. CiteSeerX   10.1.1.202.6462 . дои : 10.1111/j.1468-0084.2004.00086.x . S2CID   16972099 . Архивировано из оригинала (PDF) 5 мая 2004 года.
• Джини, Коррадо (1912). Изменчивость и изменчивость . Бибкод : 1912vamu.book.....G . Перепечатано в Пизетти, Э.; Сальвемини Т., ред. (1955). Мемуары статистической методологии . Рим: Книжный магазин Эреди Вирджилио Вески.
• Джини, Коррадо (1921). «Измерение неравенства доходов» . Экономический журнал . 31 (121): 124–126. дои : 10.2307/2223319 . JSTOR   2223319 .
• Джорджи, Джованни Мария (1990). «Библиографический портрет коэффициента концентрации Джини» (PDF) . Метрон . 48 : 183–231. Архивировано из оригинала (PDF) 4 августа 2016 года.
• Карагианнис, Э.; Ковачевич, М. (2000). «Метод расчета оценщика отклонения складного ножа для коэффициента Джини». Оксфордский бюллетень экономики и статистики . 62 : 119–122. дои : 10.1111/1468-0084.00163 .
• Миллс, Джеффри А.; Зандвакили, Суруше (1997). «Статистический вывод с помощью начальной загрузки для измерения показателей неравенства» (PDF) . Журнал прикладной эконометрики . 12 (2): 133–150. CiteSeerX   10.1.1.172.5003 . doi : 10.1002/(SICI)1099-1255(199703)12:2<133::AID-JAE433>3.0.CO;2-H . hdl : 10419/186818 . JSTOR   2284908 . Архивировано (PDF) из оригинала 18 июля 2012 года.
• Модаррес, Реза; Гаствирт, Джозеф Л. (2006). «Предостережение по оценке стандартной ошибки индекса неравенства Джини». Оксфордский бюллетень экономики и статистики . 68 (3): 385–390. дои : 10.1111/j.1468-0084.2006.00167.x . S2CID   122716409 .
• Морган, Джеймс (1962). «Анатомия распределения доходов». Обзор экономики и статистики . 44 (3): 270–283. дои : 10.2307/1926398 . JSTOR   1926398 .
• Огванг, Томсон (2000). «Удобный метод расчета индекса Джини и его стандартной ошибки». Оксфордский бюллетень экономики и статистики . 62 : 123–129. дои : 10.1111/1468-0084.00164 .
• Огванг, Томсон (2004). «Расчет стандартной ошибки для коэффициента Джини: некоторые дополнительные результаты: ответ». Оксфордский бюллетень экономики и статистики . 66 (3): 435–437. дои : 10.1111/j.1468-0084.2004.00087.x . S2CID   122160535 .
• Сюй, Куан (январь 2004 г.). «Как развивалась литература об индексе Джини за последние 80 лет?» (PDF) . Электронный журнал ССРН . Рабочий документ по экономике. Университет Далхаузи . дои : 10.2139/ssrn.423200 . Архивировано из оригинала (PDF) 28 сентября 2006 года . Проверено 1 июня 2006 г. Китайская версия этой статьи была опубликована как Сюй, Куан (2003). «Как изменилась литература об индексе Джини за последние 80 лет?». Ежеквартальный экономический журнал Китая . 2 : 757–778.
• Ицхаки, Шломо (1991). «Расчет оценок дисперсии складного ножа для параметров метода Джини». Журнал деловой и экономической статистики . 9 (2): 235–239. дои : 10.2307/1391792 . JSTOR   1391792 .

Внешние ссылки

• Deutsche Bundesbank: Диверсифицируют ли банки кредитные портфели? , 2005 (об использовании, например, коэффициента Джини для оценки риска кредитных портфелей)
• Forbes: Во славу неравенства
• Измерение рисков программного проекта с помощью коэффициента Джини — применения коэффициента Джини к программному обеспечению.
• Всемирный банк: измерение неравенства
• Трэвис Хейл, Проект неравенства Техасского университета: Теоретические основы популярных показателей неравенства , онлайн-вычисление примеров: 1A , 1B
• Статья из The Guardian, анализирующая неравенство в Великобритании в 1974–2006 гг.
• Мировая база данных неравенства доходов
• BBC News: Что такое коэффициент Джини?
• Распределение доходов и бедность в странах ОЭСР
• Распределение доходов в США: насколько неравномерно?