Кривая Лоренца

Типичная кривая Лоренца

В экономике кривая Лоренца является графическим представлением распределения доходов или богатства . Он был разработан Максом О. Лоренцем в 1905 году для отражения неравенства в распределении богатства .

Кривая представляет собой график, показывающий долю общего дохода или богатства, получаемую беднейшими слоями x населения %, хотя это не совсем верно для конечной численности населения (см. ниже). Он часто используется для представления распределения доходов , где для нижних x % домохозяйств он показывает, какой процент ( y %) от общего дохода они имеют. Процент по домохозяйств отложен по оси X , процент доходов — Y. оси Его также можно использовать для отображения распределения активов . При таком использовании многие экономисты считают его мерой социального неравенства .

Эта концепция полезна для описания неравенства в размерах особей в экологии. и в исследованиях биоразнообразия , где совокупная доля видов отображается в зависимости от совокупной доли особей. Это также полезно при бизнес-моделировании : например, в потребительском финансировании , чтобы измерить фактический процент y % просрочек, относящихся к x % людей с наихудшими показателями риска . Кривые Лоренца также применялись в эпидемиологии и общественном здравоохранении , например, для измерения пандемического неравенства как распределения общенациональной совокупной заболеваемости (y%), генерируемой населением, проживающим на территориях (x%), ранжированных по уровню местной эпидемической заболеваемости .

Объяснение

Вывод кривой Лоренца и коэффициента Джини для мирового дохода в 2011 г.

Данные за 2005 год.

Точки на кривой Лоренца представляют собой такие утверждения, как: «Низшие 20% всех домохозяйств имеют 10% общего дохода».

Совершенно равное распределение доходов будет таким, при котором каждый человек будет иметь одинаковый доход. В этом случае нижние N % общества всегда будут иметь N % дохода. Это можно изобразить прямой линией y = x ; называется «линией совершенного равенства».

Напротив, совершенно неравномерное распределение будет таким, при котором один человек будет иметь весь доход, а все остальные его не получат. В этом случае кривая будет иметь вид y = 0 % для всех x < 100 % и y = 100 %, когда x = 100 %. Эта кривая называется «линией совершенного неравенства».

Коэффициент Джини представляет собой отношение площади между линией совершенного равенства и наблюдаемой кривой Лоренца к площади между линией совершенного равенства и линией совершенного неравенства. Чем выше коэффициент, тем более неравномерным является распределение. На диаграмме справа это определяется соотношением A /( A + B ), где A и B — площади регионов, отмеченных на диаграмме.

Определение и расчет

Кривая Лоренца распределения богатства в США в 2016 году, показывающая отрицательное богатство и олигархию

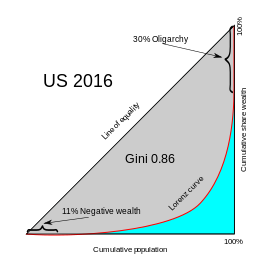
Кривая Лоренца представляет собой вероятностный график ( график P – P ), сравнивающий распределение переменной с гипотетическим равномерным распределением этой переменной. Обычно его можно представить функцией L ( F ), где F , совокупная доля населения, представлена ​​горизонтальной осью, а L , совокупная часть общего богатства или дохода, представлена ​​вертикальной осью.

Кривая L не обязательно должна быть плавно возрастающей функцией F. Для распределения богатства, например, могут существовать олигархи или люди с отрицательным богатством.

Для дискретного распределения Y, заданного значениями y ₁ , ..., y _n в неубывающем порядке ( y _i ≤ y _{i +1} ) и их вероятностей $f(y_{j}):=\Pr(Y=y_{j})$ кривая Лоренца — это непрерывная кусочно-линейная функция, соединяющая точки ( Fi _i , L _i ), i = 0, с n , где F ₀ = 0, L ₀ = 0, а для i = 1 с n : $${\begin{aligned}F_{i}&:=\sum _{j=1}^{i}f(y_{j})\\S_{i}&:=\sum _{j=1}^{i}f(y_{j})\,y_{j}\\L_{i}&:={\frac {S_{i}}{S_{n}}}\end{aligned}}$$

Когда все y _i равновероятны с вероятностями 1/ n, это упрощается до $${\begin{aligned}F_{i}&={\frac {i}{n}}\\S_{i}&={\frac {1}{n}}\sum _{j=1}^{i}\;y_{j}\\L_{i}&={\frac {S_{i}}{S_{n}}}\end{aligned}}$$

Для непрерывного распределения с функцией плотности вероятности f и кумулятивной функцией распределения F кривая Лоренца L определяется следующим образом: $$L(F(x))={\frac {\int _{-\infty }^{x}t\,f(t)\,dt}{\int _{-\infty }^{\infty }t\,f(t)\,dt}}={\frac {\int _{-\infty }^{x}t\,f(t)\,dt}{\mu }}$$где $\mu$ обозначает среднее значение. Кривую Лоренца L ( F ) можно затем построить как функцию, параметрическую по x : L ( x ) в зависимости от F ( x ). В других контекстах вычисленная здесь величина известна как распределение, смещенное по длине (или по размеру); он также играет важную роль в теории обновления.

Альтернативно, для кумулятивной функции распределения F ( x ) с обратным x ( F ) кривая Лоренца L ( F ) напрямую определяется выражением: $$L(F)={\frac {\int _{0}^{F}x(F_{1})\,dF_{1}}{\int _{0}^{1}x(F_{1})\,dF_{1}}}$$

Обратный x ( F ) может не существовать, поскольку кумулятивная функция распределения имеет интервалы постоянных значений. Однако предыдущую формулу все же можно применить, если обобщить определение x ( F ): Не удалось проанализировать (SVG (MathML можно включить через плагин браузера): неверный ответ («Расширение Math не может подключиться к Restbase.») с сервера «http://localhost:6011/en.wikipedia.org/v1/»:) : {\displaystyle x(F_1) = \inf \{y: F(y) \geq F_1\}} где inf — нижняя грань .

Пример кривой Лоренца см. в разделе Распределение Парето .

Характеристики

Практический пример кривой Лоренца: кривые Лоренца Дании, Венгрии и Намибии.

Кривая Лоренца всегда начинается в точке (0,0) и заканчивается в точке (1,1).

Кривая Лоренца не определена, если среднее значение распределения вероятностей равно нулю или бесконечно.

Кривая Лоренца для распределения вероятностей является непрерывной функцией . Однако кривые Лоренца, представляющие разрывные функции, могут быть построены как предел кривых Лоренца вероятностных распределений, примером может служить линия совершенного неравенства.

Информация на кривой Лоренца может быть суммирована коэффициентом Джини и коэффициентом асимметрии Лоренца .

Кривая Лоренца не может подняться выше линии совершенного равенства.

Кривая Лоренца, которая никогда не попадает под вторую кривую Лоренца и хотя бы один раз проходит выше нее, имеет доминирование Лоренца над второй.

Если измеряемая переменная не может принимать отрицательные значения, кривая Лоренца:

• не может опуститься ниже линии совершенного неравенства,
• увеличивается ​ .

Однако обратите внимание, что кривая Лоренца для определения собственного капитала вначале будет отрицательной из-за того, что у некоторых людей собственный капитал отрицательный из-за долгов.

Кривая Лоренца инвариантна относительно положительного масштабирования. Если X — случайная величина, для любого положительного числа c случайная величина c X имеет ту же кривую Лоренца, что X. и

Кривая Лоренца переворачивается дважды: один раз при F = 0,5 и один раз при L = 0,5 путем отрицания. Если X — случайная величина с кривой Лоренца L _X ( F ), то — X имеет кривую Лоренца:

L _{- Икс} знак равно 1 - L _Икс (1 - F )

Кривая Лоренца изменяется в результате трансляции так, что разрыв равенства F - L ( F ) изменяется пропорционально соотношению исходных и переведенных средних значений. Если X — случайная величина с кривой Лоренца L _X ( F ) и средним значением µ _X , то для любой константы c ≠ − µ _X , X + c имеет кривую Лоренца, определяемую следующим образом: $$F-L_{X+c}(F)={\frac {\mu _{X}}{\mu _{X}+c}}(F-L_{X}(F))$$

Для кумулятивной функции распределения F ( x ) со средним значением µ и (обобщенным) обратным x ( F ) тогда для любого F с 0 < F < 1 :

• Если кривая Лоренца дифференцируема: $${\frac {dL(F)}{dF}}={\frac {x(F)}{\mu }}$$
• Если кривая Лоренца дважды дифференцируема, то функция плотности вероятности f ( x ) существует в этой точке и: $${\frac {d^{2}L(F)}{dF^{2}}}={\frac {1}{\mu \,f(x(F))}}\,$$
• Если L ( F ) непрерывно дифференцируемо, то касательная к L ( F ) параллельна линии совершенного равенства в точке F ( µ ). Это также точка, в которой разрыв равенства F − L ( F ), вертикальное расстояние между кривой Лоренца и линией идеального равенства, является наибольшим. Размер разрыва равен половине относительного среднего абсолютного отклонения : $$F(\mu )-L(F(\mu ))={\frac {\text{mean absolute deviation}}{2\,\mu }}$$

См. также

• Распространение (экономика)
• Распределение богатства
• Экономика благосостояния
• Показатели неравенства доходов
• Коэффициент Джини
• Индекс Гувера (он же индекс Робин Гуда)
• ROC-анализ
• Социальное обеспечение (политология)
• Экономическое неравенство
• Закон Ципфа
• Распределение Парето
• Среднее отклонение
• Слоновья кривая

Дальнейшее чтение

• Лоренц, Миссури (1905). «Методы измерения концентрации богатства». Публикации Американской статистической ассоциации . 9 (70). Публикации Американской статистической ассоциации, Vol. 9, № 70: 209–219. Бибкод : 1905PAmSA...9..209L . дои : 10.2307/2276207 . JSTOR   2276207 . S2CID   154048722 .
• Гаствирт, Джозеф Л. (1972). «Оценка кривой Лоренца и индекса Джини». Обзор экономики и статистики . 54 (3). Обзор экономики и статистики, Vol. 54, № 3: 306–316. дои : 10.2307/1937992 . JSTOR   1937992 .
• Чакраварти, СР (1990). Цифры этического социального индекса . Нью-Йорк: Springer-Verlag. ISBN  0-387-52274-3 .
• Ананд, Судхир (1983). Неравенство и бедность в Малайзии . Нью-Йорк: Издательство Оксфордского университета. ISBN  0-19-520153-1 .

Внешние ссылки

• WIID. Архивировано 13 марта 2011 г. в Wayback Machine : World Income Inequality Database, источник информации о неравенстве, собранный WIDER (Всемирный институт исследований экономики развития, часть Университета Организации Объединенных Наций).
• glcurve : модуль Stata для построения кривой Лоренца (введите «findit glcurve» или «ssc install glcurve» в приглашении Stata для установки)
• Бесплатное дополнение к STATA для расчета показателей неравенства и бедности
• Бесплатное онлайн-программное обеспечение (калькулятор) рассчитывает коэффициент Джини, строит кривую Лоренца и вычисляет многие другие показатели концентрации для любого набора данных.
• Бесплатный калькулятор: онлайн- и загружаемые скрипты ( Python и Lua ) для неравенств Аткинсона, Джини и Гувера.
• Пользователи программного обеспечения для анализа данных R могут установить пакет «ineq», который позволяет рассчитывать различные индексы неравенства, включая Джини, Аткинсона, Тейла.
• Пакет неравенства MATLAB, заархивированный 4 октября 2008 г. в Wayback Machine , включая код для вычисления индексов Джини, Аткинсона, Тейла и для построения кривой Лоренца. Доступно множество примеров.
• Полный раздаточный материал о кривой Лоренца, включая различные приложения, включая электронную таблицу Excel с графиками кривых Лоренца и расчетом коэффициентов Джини, а также коэффициентов вариации.
• LORENZ 3.0 — это блокнот Mathematica , в котором рисуются образцы кривых Лоренца и рассчитываются коэффициенты Джини и коэффициенты асимметрии Лоренца на основе данных в листе Excel.