Математическая экономика

Математическая экономика — это применение математических методов для представления теорий и анализа проблем экономики . Часто эти прикладные методы выходят за рамки простой геометрии и могут включать дифференциальное и интегральное исчисление , разностные и дифференциальные уравнения , матричную алгебру , математическое программирование или другие вычислительные методы . Сторонники этого подхода утверждают, что он позволяет формулировать теоретические отношения со строгостью, общностью и простотой.

Математика позволяет экономистам формировать осмысленные, проверяемые положения по широкому кругу и сложным темам, которые труднее выразить неформально. Более того, язык математики позволяет экономистам делать конкретные, позитивные утверждения по спорным или спорным вопросам, которые были бы невозможны без математики. Большая часть экономической теории в настоящее время представлена ​​в виде математических экономических моделей — набора стилизованных и упрощенных математических отношений, призванных прояснить предположения и выводы.

Широкие области применения включают в себя:

• проблемы оптимизации относительно целевого равновесия, будь то домашнее хозяйство, коммерческая фирма или политик
• статический (или равновесный ) анализ, в котором экономическая единица (например, домашнее хозяйство) или экономическая система (например, рынок или экономика ) моделируется как неизменяющаяся.
• сравнительная статика относительно перехода от одного равновесия к другому, вызванного изменением одного или нескольких факторов
• динамический анализ, отслеживающий изменения в экономической системе с течением времени, например, в результате экономического роста .

Формальное экономическое моделирование началось в 19 веке с использования дифференциального исчисления для представления и объяснения экономического поведения, такого как максимизация полезности , раннее экономическое применение математической оптимизации . Экономика как дисциплина стала более математической в ​​течение первой половины 20-го века, но введение новых и обобщенных методов в период Второй мировой войны , таких как теория игр , значительно расширило бы использование математических формулировок в экономике.

Такая быстрая систематизация экономики встревожила критиков этой дисциплины, а также некоторых известных экономистов. Джон Мейнард Кейнс , Роберт Хейлбронер , Фридрих Хайек и другие критиковали широкое использование математических моделей человеческого поведения, утверждая, что некоторые человеческие решения не сводятся к математике.

История

Основная статья: История экономической мысли

Использование математики для социального и экономического анализа восходит к 17 веку. Затем, главным образом в немецких университетах, появился стиль обучения, который конкретно касался подробного представления данных, связанных с государственным управлением. Готфрид Ахенвалль читал лекции таким образом, придумав термин «статистика» . В то же время небольшая группа профессоров в Англии разработала метод «рассуждения с помощью цифр о вещах, касающихся правительства» и назвала эту практику « политической арифметикой » . Сэр Уильям Петти подробно писал о вопросах, которые позже будут волновать экономистов, таких как налогообложение, скорость обращения денег и национальный доход , но, хотя его анализ был численным, он отверг абстрактную математическую методологию. Использование Петти подробных числовых данных (вместе с Джоном Граунтом ) в течение некоторого времени будет влиять на статистиков и экономистов, хотя работы Петти в значительной степени игнорировались английскими учеными.

Математизация экономики началась всерьез в XIX веке. Большая часть экономического анализа того времени представляла собой то, что позже будет названо классической экономикой . Предметы обсуждались и обходились алгебраическими средствами, но исчисление не использовалось. Что еще более важно, до выхода книги Иоганна Генриха фон Тюнена в «Изолированное государство» 1826 году экономисты не разрабатывали явных и абстрактных моделей поведения, чтобы применять инструменты математики. Модель использования сельскохозяйственных земель Тюнена представляет собой первый пример маржинального анализа. Работа Тюнена была в основном теоретической, но он также собирал эмпирические данные, чтобы попытаться подтвердить свои обобщения. По сравнению со своими современниками, Тюнен создавал экономические модели и инструменты, а не применял предыдущие инструменты для решения новых проблем.

Тем временем новая группа ученых, обученных математическим методам физических наук, тяготела к экономике, защищая и применяя эти методы к своему предмету. и описывается сегодня как переход от геометрии к механике . В их число входил У.С. Джевонс , который в 1862 году представил статью об «общей математической теории политической экономии», предоставив схему использования теории предельной полезности в политической экономии. В 1871 году он опубликовал «Принципы политической экономии» , заявив, что предмет как наука «должен быть математическим просто потому, что он имеет дело с количествами». Джевонс ожидал, что только сбор статистических данных о ценах и количествах позволит предмету в его представлении стать точной наукой. Другие предшествовали и следовали за ними в расширении математических представлений экономических проблем .

корни неоклассической

Основная статья: Маржинализм

Равновесные количества как решение двух реакционных функций в дуополии Курно. Каждая функция реакции выражается в виде линейного уравнения, зависящего от требуемого количества.

Огюстен Курно и Леон Вальрас аксиоматически построили инструменты этой дисциплины вокруг полезности, утверждая, что люди стремятся максимизировать свою полезность при выборе способа, который можно описать математически. В то время считалось, что полезность можно измерить в единицах, известных как utils . Курно, Вальрас и Фрэнсис Исидро Эджворт считаются предшественниками современной математической экономики.

Огюстен Курно

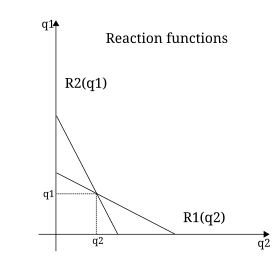
Курно, профессор математики, в 1838 году разработал математическую трактовку дуополии — состояния рынка, определяемого конкуренцией между двумя продавцами. Эта трактовка конкуренции, впервые опубликованная в «Исследованиях математических принципов богатства» , называется дуополией Курно . Предполагается, что оба продавца имели равный доступ к рынку и могли производить свои товары без затрат. Далее предполагалось, что оба товара однородны . Каждый продавец будет варьировать свой выпуск в зависимости от выпуска другого, а рыночная цена будет определяться общим объемом предложения. Прибыль каждой фирмы будет определяться путем умножения ее выпуска на рыночную цену за единицу продукции . Дифференцирование функции прибыли по объему предложения для каждой фирмы привело к получению системы линейных уравнений, одновременное решение которых дало равновесное количество, цену и прибыль. Вклад Курно в математизацию экономики десятилетиями игнорировался, но в конечном итоге оказал влияние на многих маржиналистов . Курно Модели дуополии и олигополии также представляют собой одну из первых формулировок некооперативных игр . Сегодня решение может быть дано в виде равновесия Нэша , но работа Курно опередила современную теорию игр более чем на 100 лет.

Леон Вальрас

В то время как Курно предложил решение для того, что позже будет названо частичным равновесием, Леон Вальрас попытался формализовать обсуждение экономики в целом с помощью теории общего конкурентного равновесия . Поведение каждого экономического субъекта будет рассматриваться как со стороны производства, так и со стороны потребления. Первоначально Вальрас представил четыре отдельные модели обмена, каждая из которых рекурсивно включалась в следующую. Решение полученной системы уравнений (как линейных, так и нелинейных) и есть общее равновесие. В то время невозможно было найти общее решение для системы сколь угодно большого числа уравнений, но попытки Вальраса привели к двум известным результатам в экономике. Первый — это закон Вальраса , второй — принцип tâtonnement . Метод Вальраса в то время считался в высшей степени математическим, и Эджворт подробно прокомментировал этот факт в своем обзоре «Éléments d'économie politique pure» («Элементы чистой экономики»).

Закон Вальраса был введен как теоретический ответ на проблему определения решений в условиях общего равновесия. Его обозначения отличаются от современных обозначений, но могут быть построены с использованием более современных обозначений суммирования. Вальрас предположил, что в равновесии все деньги будут потрачены на все товары: каждый товар будет продан по рыночной цене на этот товар, и каждый покупатель потратит свой последний доллар на корзину товаров. Исходя из этого предположения, Вальрас мог затем показать, что если бы было n рынков и n-1 рынков очистились (достигли состояния равновесия), то n-й рынок также очистился бы. Это проще всего представить на примере двух рынков (в большинстве текстов рассматриваемых как рынок товаров и рынок денег). Если один из двух рынков достиг состояния равновесия, никакие дополнительные товары (или, наоборот, деньги) не могут войти или выйти из второго рынка, поэтому он также должен находиться в состоянии равновесия. Вальрас использовал это утверждение, чтобы продвинуться к доказательству существования решений общего равновесия, но сегодня оно обычно используется для иллюстрации рыночного клиринга на денежных рынках на уровне бакалавриата.

Tâtonnement (примерно по-французски « нащупывание» ) должен был служить практическим выражением вальрасовского общего равновесия. Вальрас абстрагировал рынок как аукцион товаров, на котором аукционист объявлял цены, а участники рынка ждали, пока каждый из них не сможет удовлетворить свои личные резервированные цены на желаемое количество (помните, что это аукцион по всем товарам, поэтому у каждого есть резервную цену желаемой корзины товаров).

Только тогда, когда все покупатели удовлетворены данной рыночной ценой, заключаются сделки. Рынок «очистится» при этой цене — не будет ни излишка, ни дефицита. Слово tâtonnement используется для описания направлений, в которых рынок стремится к равновесию, устанавливая высокие или низкие цены на различные товары до тех пор, пока цена не будет согласована для всех товаров. Хотя этот процесс кажется динамичным, Вальрас представил лишь статическую модель, поскольку никаких транзакций не будет происходить, пока все рынки не придут в равновесие. На практике очень немногие рынки работают таким образом.

Фрэнсис

Эджворт подробно представил математические элементы в экономике в книге «Математическая психика: эссе о применении математики к моральным наукам» , опубликованной в 1881 году. Он применил Джереми Бентама к удачное исчисление экономическому поведению, позволив конвертировать результат каждого решения в изменение полезности. Используя это предположение, Эджворт построил модель обмена на трех предположениях: люди корыстны, люди действуют ради максимизации полезности и люди «свободны перезаключить договор с другим независимо от… любой третьей стороны».

Блок Эджворта, показывающий контрактную кривую экономики с двумя участниками. На современном языке это называется «ядром» экономики. На кривой кривой для экономик с двумя участниками существует бесконечно много решений.

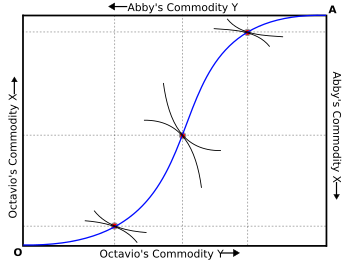
Для двух индивидуумов набор решений, при которых оба индивидуума могут максимизировать полезность, описывается контрактной кривой , которая теперь известна как ящик Эджворта . Технически конструкция решения задачи Эджворта для двух человек не была разработана графически до 1924 года Артуром Лайоном Боули . Контрактная кривая ящика Эджворта (или, в более общем плане, любого набора решений проблемы Эджворта для большего количества участников) называется ядром экономики .

Эджворт приложил значительные усилия, настаивая на том, что математические доказательства подходят для всех школ экономической мысли. Находясь у руля The Economic Journal , он опубликовал несколько статей, критикующих математическую строгость конкурирующих исследователей, в том числе Эдвина Роберта Андерсона Селигмана , известного скептика математической экономики. В статьях основное внимание уделялось вопросам налогообложения и реакции производителей. Эджворт заметил, что монополия, производящая товар, который имеет единство предложения, но не единство спроса (например, первый класс и эконом-класс в самолете, если самолет летает, оба набора сидений летают вместе с ним), может фактически снизить цену, которую видят потребители. потребитель для одного из двух товаров, если был применен налог. Здравый смысл и более традиционный численный анализ, казалось, указывали на то, что это абсурдно. Селигман настаивал на том, что результаты, достигнутые Эджвортом, были причудой его математической формулировки. Он предположил, что предположение о непрерывной функции спроса и бесконечно малом изменении налога привело к парадоксальным предсказаниям. Гарольд Хотеллинг позже показал, что Эджворт был прав и что тот же результат («уменьшение цены в результате налога») может произойти при разрывной функции спроса и больших изменениях ставки налога.

Современная математическая экономика

С конца 1930-х годов для развития экономической теории был использован ряд новых математических инструментов, таких как дифференциальное исчисление и дифференциальные уравнения, выпуклые множества и теория графов , аналогично новым математическим методам, ранее применявшимся в физике. Позднее этот процесс был описан как переход от механики к аксиоматике .

Дифференциальное исчисление

Основные статьи: Основы экономического анализа и дифференциального исчисления

См. Также: эффективность Парето и аукцион Вальраса.

Вильфредо Парето анализировал микроэкономику , рассматривая решения экономических субъектов как попытки изменить данное распределение товаров на другое, более предпочтительное распределение. Наборы распределений можно было бы тогда рассматривать как эффективные по Парето (эквивалентный термин — «оптимум по Парето»), когда между акторами не может происходить обмена, который мог бы улучшить благосостояние хотя бы одного человека, не ухудшая при этом положение другого человека. Доказательство Парето обычно путают с вальрасовским равновесием или неофициально приписывают Адама Смита » гипотезе «невидимой руки . Скорее, утверждение Парето было первым формальным утверждением того, что впоследствии стало известно как первая фундаментальная теорема экономики благосостояния . В этих моделях отсутствовали неравенства следующего поколения математической экономики.

В знаковом трактате «Основы экономического анализа» (1947) Пол Самуэльсон определил общую парадигму и математическую структуру во многих областях предмета, основываясь на предыдущей работе Альфреда Маршалла . Фонды взяли математические концепции из физики и применили их к экономическим проблемам. Этот широкий взгляд (например, сравнение принципа Ле Шателье с tâtonnement ) лежит в основе фундаментальной предпосылки математической экономики: системы экономических субъектов можно моделировать, а их поведение описывать так же, как и любую другую систему. Это расширение последовало за работой маржиналистов предыдущего столетия и значительно расширило ее. Самуэльсон подошел к проблемам применения максимизации индивидуальной полезности к совокупным группам с помощью сравнительной статики , которая сравнивает два разных равновесия состояния после экзогенного изменения переменной. Этот и другие методы, представленные в книге, легли в основу математической экономики ХХ века.

Линейные модели

См. также: Линейная алгебра , Линейное программирование и теорема Перрона – Фробениуса.

Ограниченные модели общего равновесия были сформулированы Джоном фон Нейманом в 1937 году. В отличие от более ранних версий, модели фон Неймана имели ограничения-неравенства. Для своей модели расширяющейся экономики фон Нейман доказал существование и единственность равновесия, используя свое обобщение теоремы Брауэра о неподвижной точке . Модель фон Неймана расширяющейся экономики рассматривала матричный пучок   A - λ B с неотрицательными матрицами A и B ; фон Нейман искал вероятности векторы   p и q и положительное число λ, которые позволили бы решить дополнительности уравнение .

п ^Т ( А - λ B ) q = 0,

наряду с двумя системами неравенства, выражающими экономическую эффективность. В этой модели ( транспонированный ) вектор вероятности p представляет цены на товары, а вектор вероятности q представляет «интенсивность», с которой будет работать производственный процесс. Единственное решение λ представляет темпы роста экономики, которые равны процентной ставке . Доказательство существования положительных темпов роста и доказательство того, что темпы роста равны процентной ставке, были выдающимися достижениями даже для фон Неймана. Результаты фон Неймана рассматривались как частный случай линейного программирования , где модель фон Неймана использует только неотрицательные матрицы. Исследование модели расширяющейся экономики фон Неймана продолжает интересовать экономистов-математиков, интересующихся вычислительной экономикой.

Экономика «затраты-выпуск»

Основная статья: Модель ввода-вывода

В 1936 году экономист российского происхождения Василий Леонтьев построил свою модель анализа затрат-выпуска на основе таблиц «материального баланса», построенных советскими экономистами, которые сами следовали более ранним работам физиократов . С помощью своей модели, описывающей систему процессов производства и спроса, Леонтьев описал, как изменения спроса в одном секторе экономики повлияют на производство в другом. На практике Леонтьев оценивал коэффициенты своих простых моделей для решения экономически интересных вопросов. В экономике производства «технологии Леонтьева» производят продукцию с использованием постоянных пропорций ресурсов, независимо от цены ресурсов, что снижает ценность моделей Леонтьева для понимания экономики, но позволяет относительно легко оценить их параметры. Напротив, модель фон Неймана расширяющейся экономики допускает выбор методов , но коэффициенты необходимо оценивать для каждой технологии.

Математическая оптимизация

Красная точка в направлении z как максимум для параболоидной функции входных сигналов (x, y)

Основные статьи: Математическая оптимизация и двойная задача

См. Также: Выпуклость в экономике и Невыпуклость (экономика).

В математике математическая оптимизация (или оптимизация или математическое программирование) относится к выбору лучшего элемента из некоторого набора доступных альтернатив. В простейшем случае задача оптимизации включает в себя максимизацию или минимизацию реальной функции путем выбора входных значений функции и вычисления соответствующих значений функции. Процесс решения включает в себя выполнение общих необходимых и достаточных условий оптимальности . Для задач оптимизации могут использоваться специальные обозначения функции и ее входных данных. В более общем смысле оптимизация включает в себя поиск наилучшего доступного элемента некоторой функции в заданной области и может использовать множество различных методов вычислительной оптимизации .

Экономика настолько тесно связана с оптимизацией агентов экономики , что влиятельное определение описывает экономику как науку как «изучение человеческого поведения как взаимосвязи между целями и ограниченными средствами» с альтернативными видами использования. Проблемы оптимизации пронизывают современную экономику, многие из которых имеют явные экономические или технические ограничения. В микроэкономике проблема максимизации полезности и ее двойная проблема — задача минимизации расходов для заданного уровня полезности — являются задачами экономической оптимизации. Теория утверждает, что потребители максимизируют свою полезность с учетом своих бюджетных ограничений , а фирмы максимизируют свою прибыль с учетом своих производственных функций , затрат на вводимые ресурсы и рыночного спроса .

Экономическое равновесие изучается в теории оптимизации как ключевой ингредиент экономических теорем, которые в принципе можно проверить на эмпирических данных. Новые разработки произошли в области динамического программирования и оптимизации моделирования с учетом риска и неопределенности , включая приложения к теории портфеля , экономике информации и теории поиска .

Свойства оптимальности для всей рыночной системы могут быть сформулированы в математических терминах, например, при формулировке двух фундаментальных теорем экономики благосостояния. и в Эрроу – Дебре модели общего равновесия (также обсуждаемой ниже ). Говоря конкретнее, многие задачи поддаются аналитическому (формульному) решению. Многие другие могут быть достаточно сложными, чтобы требовать численных методов решения с помощью программного обеспечения. Третьи являются сложными, но достаточно понятными, чтобы обеспечить вычислимые методы решения, в частности, вычислимые модели общего равновесия для всей экономики.

Линейное и нелинейное программирование глубоко повлияло на микроэкономику, которая ранее рассматривала только ограничения равенства. Многие экономисты-математики, получившие Нобелевскую премию по экономике, провели заметные исследования с использованием линейного программирования: Леонид Канторович , Леонид Гурвич , Тьяллинг Купманс , Кеннет Дж. Эрроу , Роберт Дорфман , Пол Самуэльсон и Роберт Солоу . И Канторович, и Купманс признали, что Джордж Б. Данциг заслужил разделить Нобелевскую премию по линейному программированию. Экономисты, проводившие исследования в области нелинейного программирования, также получили Нобелевскую премию, в частности Рагнар Фриш , а также Канторович, Гурвич, Купманс, Эрроу и Самуэльсон.

Линейная оптимизация

Основные статьи: Линейное программирование и симплексный алгоритм

Линейное программирование было разработано для облегчения распределения ресурсов на предприятиях и в отраслях в 1930-е годы в России и в 1940-е годы в США. Во время воздушной перевозки в Берлин (1948 г.) линейное программирование использовалось для планирования доставки грузов, чтобы предотвратить голод в Берлине после советской блокады.

Нелинейное программирование

См. также: Нелинейное программирование , множитель Лагранжа , условия Каруша – Куна – Такера и теневая цена.

Расширение нелинейной оптимизации с ограничениями-неравенствами было достигнуто в 1951 году Альбертом В. Такером и Гарольдом Куном , которые рассматривали проблему нелинейной оптимизации :

Свернуть $f(x)$ при условии $g_{i}(x)\leq 0$ и $h_{j}(x)=0$ где

$f(\cdot )$ это функция, которую нужно минимизировать

$g_{i}(\cdot )$ являются функциями $m$ неравенства ограничения , где $i=1,\dots ,m$

$h_{j}(\cdot )$ являются функциями $l$ ограничения равенства, где $j=1,\dots ,l$.

Допуская ограничения-неравенства, подход Куна-Такера обобщил классический метод множителей Лагранжа , который (до этого) допускал только ограничения-равенства. Подход Куна-Такера вдохновил на дальнейшие исследования лагранжевой двойственности, включая рассмотрение ограничений-неравенств. Теория двойственности нелинейного программирования особенно удовлетворительна при применении к выпуклой минимизации , в которых используется выпукло-аналитическая теория двойственности Фенчела задачам и Рокафеллара ; эта выпуклая двойственность особенно сильна для многогранных выпуклых функций , например тех, которые возникают в линейном программировании . Лагранжева двойственность и выпуклый анализ ежедневно используются при исследовании операций , при планировании работы электростанций, планировании производственных графиков заводов и составлении маршрутов авиакомпаний (маршруты, рейсы, самолеты, экипажи).

и

См. также: Вариационное исчисление , Оптимальное управление и Динамическое программирование.

Экономическая динамика допускает изменения экономических переменных с течением времени, в том числе в динамических системах . Проблема поиска оптимальных функций при таких изменениях изучается в вариационном исчислении и теории оптимального управления . Перед Второй мировой войной Фрэнк Рэмси и Гарольд Хотеллинг использовали для этой цели вариационное исчисление.

Следуя работе Ричарда Беллмана по динамическому программированию и английскому переводу 1962 года Л. Понтрягина и др ., более ранней работы теория оптимального управления более широко использовалась в экономике при решении динамических проблем, особенно в отношении равновесия экономического роста и стабильности экономических систем, хрестоматийным примером является оптимальное потребление и сбережение . Принципиальное различие существует между детерминистическими и стохастическими моделями управления. Другие приложения теории оптимального управления включают, например, области финансов, запасов и производства.

Функциональный анализ

См. также: Функциональный анализ , Выпуклое множество , Опорная гиперплоскость , Теорема Хана – Банаха , Теорема о неподвижной точке и Двойное пространство.

в ходе доказательства существования оптимального равновесия в своей модели экономического роста Именно 1937 года Джон фон Нейман представил методы функционального анализа для включения топологии в экономическую теорию, в частности, теорию фиксированной точки, посредством своего обобщения теории фиксированной точки Брауэра. точечная теорема . Следуя программе фон Неймана, Кеннет Эрроу и Жерар Дебре сформулировали абстрактные модели экономического равновесия, используя выпуклые множества и теорию фиксированной точки. Введя модель Эрроу-Дебре в 1954 году, они доказали существование (но не единственность) равновесия, а также доказали, что каждое равновесие Вальраса является эффективным по Парето ; в общем, равновесия не обязательно должны быть уникальными. В их моделях («первичное») векторное пространство представляло количества, а «двойное» векторное пространство представляло цены .

В России математик Леонид Канторович разработал экономические модели в частично упорядоченных векторных пространствах , которые подчеркивали двойственность между количествами и ценами. Канторович переименовал цены в «объективно определенные оценки», которые по-русски сокращались до «о.о.о.», намекая на сложность обсуждения цен в Советском Союзе.

Даже в конечных измерениях концепции функционального анализа пролили свет на экономическую теорию, особенно в разъяснении роли цен как нормальных векторов к гиперплоскости, поддерживающей выпуклое множество, представляющее возможности производства или потребления. Однако проблемы описания оптимизации во времени или в условиях неопределенности требуют использования бесконечномерных функциональных пространств, поскольку агенты делают выбор между функциями или случайными процессами .

и

См. также: Глобальный анализ , Категория Бэра и лемма Сарда.

Джона фон Неймана Работа по функциональному анализу и топологии открыла новые горизонты в математике и экономической теории. Это также оставило передовую математическую экономику с меньшим количеством применений дифференциального исчисления. В частности, теоретики общего равновесия использовали общую топологию , выпуклую геометрию и теорию оптимизации больше, чем дифференциальное исчисление, поскольку подход дифференциального исчисления не смог установить существование равновесия.

Однако упадок дифференциального исчисления не следует преувеличивать, поскольку дифференциальное исчисление всегда использовалось в аспирантуре и в приложениях. Более того, дифференциальное исчисление вернулось на высшие уровни математической экономики, в теорию общего равновесия (GET), практикуемую « GET-множеством » (юмористическое обозначение, данное Жаку Э. Дрезу ). Однако в 1960-х и 1970-х годах Жерар Дебре и Стивен Смейл возглавили возрождение использования дифференциального исчисления в математической экономике. В частности, они смогли доказать существование общего равновесия там, где предыдущие авторы потерпели неудачу, благодаря своей новой математике: категории Бэра из общей топологии и леммы Сарда из дифференциальной топологии . Среди других экономистов, связанных с использованием дифференциального анализа, — Эгберт Диркер, Андреу Мас-Колелл и Ив Баласко . Эти достижения изменили традиционное повествование об истории математической экономики, последовавшее за фон Нейманом, который прославлял отказ от дифференциального исчисления.

Теория игр

Основная статья: Теория игр

См. также: Теория кооперативных игр ; Теория некооперативных игр ; Джон фон Нейман ; Теория игр и экономического поведения ; и Джон Форбс Нэш-младший.

Джон фон Нейман, работая с Оскаром Моргенштерном над теорией игр , открыл новые математические основы в 1944 году, распространив методы функционального анализа, связанные с выпуклыми множествами и топологической теорией неподвижной точки, на экономический анализ. Таким образом, их работа избегала традиционного дифференциального исчисления , для которого оператор максимума не применялся к недифференцируемым функциям. Продолжая работу фон Неймана в области теории кооперативных игр , теоретики игр Ллойд С. Шепли , Мартин Шубик , Эрве Мулен , Нимрод Мегиддо , Бецалель Пелег оказали влияние на экономические исследования в области политики и экономики. Например, исследование справедливых цен в кооперативных играх и справедливой стоимости игр с голосованием привело к изменению правил голосования в законодательных органах и учета затрат в проектах общественных работ. Например, теория кооперативных игр использовалась при проектировании системы водоснабжения в Южной Швеции и при установлении тарифов на выделенные телефонные линии в США.

Ранее неоклассическая теория ограничивала только диапазон результатов переговоров и в особых случаях, например, двустороннюю монополию или контрактную кривую ящика Эджворта . Результаты фон Неймана и Моргенштерна были столь же слабыми. Однако, следуя программе фон Неймана, Джон Нэш использовал теорию неподвижной точки, чтобы доказать условия, при которых задача торга и некооперативные игры могут генерировать единственное равновесное решение. Некооперативная теория игр была принята в качестве фундаментального аспекта экспериментальной экономики . поведенческая экономика , информационная экономика , промышленная организация , и политическая экономия . Это также привело к возникновению темы проектирования механизмов (иногда называемой теорией обратной игры), которая имеет приложения в частной и государственной политике в отношении способов повышения экономической эффективности посредством стимулирования обмена информацией.

В 1994 году Нэш, Джон Харсаньи и Рейнхард Зельтен получили Нобелевскую премию по экономике за работу над некооперативными играми. Харсаньи и Зельтен были награждены за работу над повторными партиями . Более поздние работы распространили свои результаты на вычислительные методы моделирования.

вычислительная

Основная статья: Агентная вычислительная экономика

Агентно-ориентированная вычислительная экономика (ACE) как названная область возникла относительно недавно, начиная примерно с 1990-х годов по опубликованным работам. Он изучает экономические процессы, включая целую экономику , как динамические системы взаимодействующих агентов во времени. Как таковая, она попадает в парадигму систем сложных адаптивных . В соответствующих агентно-ориентированных моделях агенты — это не реальные люди, а «вычислительные объекты, смоделированные как взаимодействующие в соответствии с правилами»… «чьи взаимодействия на микроуровне создают возникающие закономерности» в пространстве и времени. Правила сформулированы для прогнозирования поведения и социальных взаимодействий на основе стимулов и информации. Теоретическое предположение о математической оптимизации рынков агентов заменяется менее ограничительным постулатом об агентах с ограниченной рациональностью , адаптирующихся к рыночным силам.

Модели ACE применяют численные методы анализа для компьютерного моделирования сложных динамических задач, для решения которых более традиционные методы, такие как формулирование теорем, не могут найти готового применения. Начиная с заданных начальных условий, вычислительная экономическая система моделируется как развивающаяся с течением времени, поскольку ее составляющие агенты неоднократно взаимодействуют друг с другом. В этом отношении ACE можно охарактеризовать как восходящий культурный подход к изучению экономики. В отличие от других стандартных методов моделирования, события ACE управляются исключительно начальными условиями, независимо от того, существуют ли равновесия или их можно вычислить. Однако моделирование ACE включает адаптацию, автономию и обучение агентов. Она имеет сходство и совпадение с теорией игр как агентным методом моделирования социальных взаимодействий. Другие аспекты подхода включают такие стандартные экономические предметы, как конкуренция и сотрудничество . структура рынка и промышленная организация , транзакционные издержки , экономика благосостояния и конструкция механизма , информация и неопределенность , и макроэкономика .

Говорят, что этот метод выигрывает от постоянного совершенствования методов моделирования в области информатики и расширения компьютерных возможностей. В число проблем входят те, которые являются общими для экспериментальной экономики в целом. и в сравнении и к разработке общей структуры для эмпирической проверки и решения открытых вопросов в агентном моделировании. Конечная научная цель метода была описана как «проверка теоретических результатов на реальных данных таким образом, чтобы позволить эмпирически подтвержденным теориям накапливаться с течением времени, при этом работа каждого исследователя должным образом основывается на предыдущей работе».

Математизация экономики

Поверхность улыбки волатильности представляет собой трехмерную поверхность, на которой текущая рыночная подразумеваемая волатильность (ось Z) для всех опционов базового актива отображается в зависимости от цены исполнения и времени до погашения (оси X и Y).

На протяжении ХХ века статьи в «основных журналах» по экономике почти исключительно написаны экономистами из академических кругов . В результате большая часть материалов, передаваемых в этих журналах, относится к экономической теории, а «сама экономическая теория постоянно становилась все более абстрактной и математической». Субъективная оценка математических методов Работающие в этих профильных журналах показали снижение количества статей, в которых не используются ни геометрические представления, ни математические обозначения, с 95% в 1892 году до 5,3% в 1990 году. Опрос десяти ведущих экономических журналов, проведенный в 2007 году, показал, что только 5,8% статей, опубликованных в 2003 и 2004 годах, не содержали статистического анализа данных и не содержали математических выражений, которые были пронумерованы цифрами на полях страницы.

Эконометрика

Основная статья: Эконометрика

В период между мировыми войнами достижения в области математической статистики и кадры экономистов с математическим образованием привели к появлению эконометрики — названия, предложенного для дисциплины, развивающей экономику с помощью математики и статистики. В экономике «эконометрика» часто использовалась для статистических методов в экономике, а не для математической экономики. Статистическая эконометрика предполагает применение линейной регрессии и анализа временных рядов к экономическим данным.

Рагнар Фриш придумал слово «эконометрика» и помог основать Эконометрическое общество в 1930 году и журнал «Эконометрика» в 1933 году. Ученик Фриша Трюгве Хаавельмо опубликовал «Вероятностный подход в эконометрике» в 1944 году, где утверждал, что точный статистический анализ может использоваться в качестве инструмента для проверки математических теорий об экономических субъектах с помощью данных из сложных источников. Эта связь статистического анализа систем с экономической теорией также пропагандировалась Комиссией Коулза (ныне Фонд Коулза ) на протяжении 1930-х и 1940-х годов.

Корни современной эконометрики можно проследить до американского экономиста Генри Л. Мура . Мур изучал продуктивность сельского хозяйства и пытался подогнать изменяющиеся значения урожайности участков кукурузы и других культур к кривой, используя различные значения эластичности. Мур допустил несколько ошибок в своей работе, некоторые из-за выбора моделей, а некоторые из-за ограничений в использовании математики. Точность моделей Мура также была ограничена плохими данными национальных счетов в Соединенных Штатах в то время. Хотя его первые модели производства были статичными, в 1925 году он опубликовал динамическую модель «движущегося равновесия», призванную объяснить бизнес-циклы — это периодическое изменение в результате чрезмерной коррекции кривых спроса и предложения теперь известно как модель паутины . Более формальный вывод этой модели был сделан позже Николасом Калдором , которому во многом приписывают ее изложение.

Приложение

Модель IS/LM представляет собой кейнсианскую макроэкономическую модель, предназначенную для прогнозирования пересечения «реальной» экономической деятельности (например, расходов, доходов , норм сбережений) и решений, принимаемых на финансовых рынках ( предпочтение денежной массы и ликвидности ). Эта модель больше не широко преподается на уровне аспирантов, но широко используется на курсах бакалавриата по макроэкономике.

Большая часть классической экономики может быть представлена ​​в простых геометрических терминах или элементарных математических обозначениях. Однако математическая экономика традиционно использует исчисление и матричную алгебру в экономическом анализе, чтобы сделать убедительные утверждения, которые были бы более трудными без таких математических инструментов. Эти инструменты являются предпосылками для формального изучения не только математической экономики, но и современной экономической теории в целом. Экономические проблемы часто включают в себя так много переменных, что математика является единственным практическим способом их решения. Альфред Маршалл утверждал, что каждую экономическую проблему, которую можно определить количественно, аналитически выразить и решить, следует решать посредством математической работы.

Экономика стала все больше зависеть от математических методов, а математические инструменты, которые она использует, стали более сложными. В результате математика стала значительно более важной для специалистов в области экономики и финансов. Программы магистратуры как по экономике, так и по финансам требуют серьезной подготовки по математике для поступления и по этой причине привлекают все большее число математиков . Прикладные математики применяют математические принципы к практическим проблемам, таким как экономический анализ и другие вопросы, связанные с экономикой, и многие экономические проблемы часто определяются как интегрированные в сферу прикладной математики.

Эта интеграция является результатом формулирования экономических проблем в виде стилизованных моделей с четкими предположениями и фальсифицируемыми прогнозами. Это моделирование может быть неформальным или прозаическим, как это было в Адама Смита » «Богатстве народов , или оно может быть формальным, строгим и математическим.

В широком смысле формальные экономические модели можно классифицировать как стохастические или детерминистические, а также как дискретные или непрерывные. На практическом уровне количественное моделирование применяется во многих областях экономики, и некоторые методологии развивались более или менее независимо друг от друга.

• Стохастические модели формулируются с использованием случайных процессов . Они моделируют экономически наблюдаемые значения с течением времени. Большая часть эконометрики основана на статистике для формулирования и проверки гипотез об этих процессах или оценки их параметров. Между мировыми войнами Герман Вольд разработал представление о стационарных случайных процессах с точки зрения моделей авторегрессии и детерминистской тенденции. Уолд и Ян Тинберген применили анализ временных рядов к экономическим данным. Современные исследования временных рядов статистики рассматривают дополнительные формулировки стационарных процессов, такие как модели авторегрессии скользящего среднего . Более общие модели включают модели авторегрессионной условной гетероскедастичности (ARCH) и обобщенные ARCH ( GARCH ). модели
• Нестохастические математические модели могут быть чисто качественными (например, модели, задействованные в каком-либо аспекте теории социального выбора ) или количественными (включающими рационализацию финансовых переменных, например, с помощью гиперболических координат и/или конкретных форм функциональных связей между переменными). В некоторых случаях экономические прогнозы модели просто утверждают направление движения экономических переменных, поэтому функциональные зависимости используются только в качественном смысле: например, если цена товара увеличивается, то спрос на этот товар уменьшится. . Для таких моделей экономисты часто используют двумерные графики вместо функций.
• качественные модели Иногда используются . Одним из примеров является качественное сценарное планирование , в котором разыгрываются возможные будущие события. Другим примером является нечисловой анализ дерева решений. Качественные модели часто страдают от недостаточной точности.

Пример: влияние снижения корпоративного налога на заработную плату

Огромная привлекательность математической экономики заключается в том, что она привносит определенную строгость в экономическое мышление, особенно в отношении острых политических тем. Например, во время обсуждения эффективности снижения корпоративного налога для повышения заработной платы работников простая математическая модель оказалась полезной для понимания рассматриваемых проблем.

поставил следующую задачу В качестве интеллектуального упражнения профессор Грег Мэнкью из Гарвардского университета :

Открытая экономика имеет производственную функцию. ${\textstyle y=f(k)}$, где ${\textstyle y}$ - выпуск на одного работника и ${\textstyle k}$ это капитал на одного работника. Запас капитала корректируется таким образом, что предельный продукт капитала после уплаты налогов равен экзогенно заданной мировой процентной ставке. ${\textstyle r}$...Насколько снижение налогов повысит зарплаты?

Чтобы ответить на этот вопрос, мы следуем за Джоном Х. Кокрейном из Гуверовского института . Предположим, открытая экономика имеет производственную функцию :

$$Y=F(K,L)=f(k)L,\quad k=K/L$$

Где переменные в этом уравнении:

• ${\textstyle Y}$ общий объем выпуска
• ${\textstyle F(K,L)}$ это производственная функция
• ${\textstyle K}$ это общий акционерный капитал
• ${\textstyle L}$ общий запас рабочей силы

Стандартным выбором производственной функции является производственная функция Кобба-Дугласа :

$$Y=AK^{\alpha }L^{1-\alpha }=Ak^{\alpha }L,\quad \alpha \in [0,1]$$

где ${\textstyle A}$ – коэффициент производительности , который считается постоянным. Снижение корпоративного налога в этой модели эквивалентно налогу на капитал. С помощью налогов фирмы стремятся максимизировать:

$$J=\max _{K,L}\;(1-\tau )\left[F(K,L)-wL\right]-rK\equiv \max _{K,L}\;(1-\tau )\left[f(k)-w\right]L-rK$$

где ${\textstyle \tau }$ - ставка налога на капитал, ${\textstyle w}$ - заработная плата на одного работника, а ${\textstyle r}$ экзогенная процентная ставка. Тогда условия оптимальности первого порядка примут вид:

$${\begin{aligned}{\frac {\partial J}{\partial K}}&=(1-\tau )f'(k)-r\\{\frac {\partial J}{\partial L}}&=(1-\tau )\left[f(k)-f'(k)k-w\right]\end{aligned}}$$

Следовательно, из условий оптимальности следует, что:

$$r=(1-\tau )f'(k),\quad w=f(k)-f'(k)k$$

Определить общую сумму налогов ${\textstyle X=\tau [F(K,L)-wL]}$. Это означает, что налоги на одного работника ${\textstyle x}$ являются:

$$x=\tau [f(k)-w]=\tau f'(k)k$$

Тогда изменение налогов на одного работника с учетом ставки налога составит:

$${dx \over {d\tau }}=\underbrace {f'(k)k} _{\text{Static}}+\underbrace {\tau \left[f'(k)+f''(k)k\right]{dk \over {d\tau }}} _{\text{Dynamic}}$$

Чтобы найти изменение заработной платы, дифференцируем второе условие оптимальности заработной платы на одного работника, чтобы получить:

$${\frac {dw}{d\tau }}=\left[f'(k)-f'(k)-f''(k)k\right]{\frac {dk}{d\tau }}=-f''(k)k{\frac {dk}{d\tau }}$$

Если предположить, что процентная ставка фиксирована на уровне ${\textstyle r}$, так что ${\textstyle dr/d\tau =0}$, мы можем дифференцировать первое условие оптимальности процентной ставки, чтобы найти:

$${dk \over {d\tau }}={f'(k) \over {(1-\tau )f''(k)}}$$

На данный момент давайте сосредоточимся только на статическом эффекте снижения налога на капитал, так что ${\textstyle dx/d\tau =f'(k)k}$. Если мы подставим это уравнение в уравнение изменения заработной платы в зависимости от ставки налога, то обнаружим, что:

$${dw \over {d\tau }}=-{\frac {f'(k)k}{1-\tau }}=-{1 \over {1-\tau }}{\frac {dx}{d\tau }}$$

Таким образом, статический эффект снижения налога на капитал на заработную плату составляет:

$${dw \over {dx}}=-{1 \over {1-\tau }}$$

Исходя из модели, кажется возможным, что мы сможем добиться повышения заработной платы работника, превышающего сумму снижения налогов. Но это учитывает только статический эффект, а мы знаем, что необходимо учитывать динамический эффект. В динамической модели мы можем переписать уравнение изменения налогов на одного работника в зависимости от ставки налога следующим образом:

$${\begin{aligned}{dx \over {d\tau }}&=f'(k)k+\tau \left[f'(k)+f''(k)k\right]{dk \over {d\tau }}\\&=f'(k)k+{\tau \over {1-\tau }}{[f'(k)]^{2}+f'(k)f''(k)k \over {f''(k)}}\\&={\tau \over {1-\tau }}{f'(k)^{2} \over {f''(k)}}+{1 \over {1-\tau }}f'(k)k\\&={f'(k) \over {1-\tau }}\left[\tau {f'(k) \over {f''(k)}}+k\right]\end{aligned}}$$

напоминая, что ${\textstyle dw/d\tau =-f'(k)k/(1-\tau )}$, у нас есть это:

$${\frac {dw}{dx}}=-{{\frac {f'(k)k}{1-\tau }} \over {{\frac {f'(k)}{1-\tau }}\left[\tau {\frac {f'(k)}{f''(k)}}+k\right]}}=-{\frac {1}{\tau {\frac {f'(k)}{kf''(k)}}+1}}$$

Используя производственную функцию Кобба-Дугласа, мы имеем:

$${f'(k) \over {kf''(k)}}=-{1 \over {1-\alpha }}$$

Таким образом, динамический эффект снижения налога на капитал на заработную плату составляет:

$${dw \over {dx}}=-{1-\alpha \over {1-\tau -\alpha }}$$

Если мы возьмем ${\textstyle \alpha =\tau =1/3}$, то динамический эффект от снижения налога на капитал на заработную плату будет даже больше, чем статический эффект. Более того, если существуют положительные внешние эффекты для накопления капитала , влияние снижения налогов на заработную плату будет больше, чем в модели, которую мы только что вывели. Важно отметить, что результат представляет собой комбинацию:

1. Стандартный результат: в небольшой открытой экономике труд несет 100% налога на доход от малого капитала.
2. Тот факт, что, начиная с положительной ставки налога, бремя повышения налога превышает сбор доходов из-за безвозвратных потерь первого порядка.

Этот результат, показывающий, что при определенных предположениях снижение корпоративного налога может повысить заработную плату работников больше, чем потерянный доход, не означает, что величина верна. Скорее, он предлагает основу для политического анализа, которая не основана на махинациях руками. Если предположения разумны, то модель является приемлемым приближением к реальности; если это не так, то следует разработать более совершенные модели.

Производственная функция CES

Теперь давайте предположим, что вместо производственной функции Кобба-Дугласа у нас есть более общая производственная функция с постоянной эластичностью замещения (CES) :

$$f(k)=A\left[\alpha k^{\rho }+(1-\alpha )\right]^{1/\rho }$$

где ${\textstyle \rho =1-\sigma ^{-1}}$; ${\textstyle \sigma }$ – эластичность замещения между капиталом и трудом. Соответствующая величина, которую мы хотим рассчитать, равна ${\textstyle f'/kf''}$, что может быть получено как:

$${f' \over {kf''}}=-{1 \over {1-\rho -{\alpha (1-\rho ) \over {\alpha +(1-\alpha )k^{-\rho }}}}}$$

Таким образом, мы можем использовать это, чтобы обнаружить, что:

$${\begin{aligned}1+\tau {f' \over {kf''}}&=1-{\tau [\alpha +(1-\alpha )k^{-\rho }] \over {(1-\rho )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho )}}\\[6pt]&={(1-\rho -\tau )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho ) \over {(1-\rho )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho )}}\end{aligned}}$$

Таким образом, согласно общей модели CES, динамическое влияние снижения налога на капитал на заработную плату составляет:

$${dw \over {dx}}=-{(1-\rho )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho ) \over {(1-\rho -\tau )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho )}}$$

Мы восстанавливаем решение Кобба-Дугласа, когда ${\textstyle \rho =0}$. Когда ${\textstyle \rho =1}$, что имеет место в случае существования совершенных заменителей, мы находим, что ${\textstyle dw/dx=0}$ - влияние изменения налогов на капитал на заработную плату отсутствует. И когда ${\textstyle \rho =-\infty }$, что имеет место в случае существования идеальных дополнений, мы находим, что ${\textstyle dw/dx=-1}$ - снижение налогов на капитал увеличивает заработную плату ровно на один доллар.

Критика и защита

математики для качественной и

Австрийская школа , выдвигая многие из тех же нормативных экономических аргументов, что и основные экономисты маржиналистских традиций, такие как чикагская школа отличается , методологически от основных неоклассических школ экономики, в частности, в их резкой критике математизации экономики. Фридрих Хайек утверждал, что использование формальных методов обеспечивает научную точность, которая не учитывает должным образом информационные ограничения, с которыми сталкиваются реальные экономические агенты.

В интервью 1999 года историк экономики Роберт Хейлбронер заявил:

Я думаю, что научный подход начал проникать и вскоре доминировать в профессии в последние двадцать-тридцать лет. Частично это произошло благодаря «изобретению» различного рода математического анализа и, более того, значительным усовершенствованиям в нем. Это эпоха, когда у нас не только больше данных, но и более сложное их использование. Таким образом, существует стойкое ощущение, что это наука, насыщенная данными, и предприятие, насыщенное данными, которое благодаря чистым цифрам, чистым уравнениям и внешнему виду журнальной страницы имеет определенное сходство с наукой. . . Этот центральный вид деятельности выглядит научным. Я это понимаю. Я думаю, что это искренне. Он приближается к универсальному закону. Но быть похожим на науку — это не то же самое, что быть наукой.

Хейлбронер заявил, что «некоторая / большая часть экономической науки не является по своей природе количественной и поэтому не поддается математическому изложению».

экономики

Философ Карл Поппер обсуждал научное положение экономики в 1940-х и 1950-х годах. Он утверждал, что математическая экономика страдает от тавтологичности. Другими словами, поскольку экономика стала математической теорией, математическая экономика перестала полагаться на эмпирические опровержения, а скорее опиралась на математические доказательства и опровержения. Согласно Попперу, фальсифицируемые предположения можно проверить экспериментом и наблюдением, тогда как нефальсифицируемые предположения можно исследовать математически на предмет их последствий и их согласованности с другими предположениями.

Разделяя обеспокоенность Поппера по поводу предположений в экономике в целом, а не только в математической экономике, Милтон Фридман заявил, что «все предположения нереалистичны». Фридман предложил оценивать экономические модели по их прогнозным характеристикам, а не по совпадению их предположений с реальностью.

Математическая экономика как форма чистой математики

См. также: Чистая математика , Прикладная математика и Инженерное дело.

Говоря о математической экономике, Дж. М. Кейнс писал в «Общей теории» :

Большим недостатком символических псевдоматематических методов формализации системы экономического анализа... является то, что они явно предполагают строгую независимость между участвующими факторами и теряют свою убедительность и авторитет, если эта гипотеза отвергается; тогда как в обычном дискурсе, когда мы не манипулируем слепо и все время знаем, что мы делаем и что означают слова, мы можем держать «в глубине души» необходимые резервы и квалификации, а также корректировки, которые у нас будут сделать это позже, таким образом, чтобы мы не могли держать сложные частные дифференциалы «в конце» нескольких страниц алгебры, предполагая, что все они исчезают. Слишком большая часть современной «математической» экономической теории представляет собой просто вымыслы, столь же неточные, как и первоначальные предположения, на которых они основаны, которые позволяют автору упускать из виду сложности и взаимозависимости реального мира в лабиринте претенциозных и бесполезных символов.

Защита математической экономики

В ответ на эту критику Пол Самуэльсон утверждал, что математика — это язык, повторяя тезис Джозайи Уилларда Гиббса . В экономике язык математики иногда необходим для представления существенных проблем. Более того, математическая экономика привела к концептуальному прогрессу в экономике. В частности, Самуэльсон привел пример микроэкономики , написав, что «немногие люди достаточно изобретательны, чтобы понять [ее] более сложные части... не прибегая к языку математики, в то время как большинство обычных людей могут сделать это довольно легко с помощью математика».

Некоторые экономисты заявляют, что математическая экономика заслуживает поддержки так же, как и другие формы математики, особенно ее соседи в области математической оптимизации и математической статистики и, все чаще, в теоретической информатике . Математическая экономика и другие математические науки имеют историю, в которой теоретические достижения регулярно способствовали реформированию более прикладных отраслей экономики. В частности, следуя программе Джона фон Неймана , теория игр теперь обеспечивает основу для описания большей части прикладной экономики, от статистической теории принятия решений (как «игры против природы») и эконометрики до теории общего равновесия и промышленной организации. В последнее десятилетие, с появлением Интернета, экономисты-математики, специалисты по оптимизации и ученые-компьютерщики работали над проблемами ценообразования на онлайн-услуги, используя математику из теории кооперативных игр, недифференцируемой оптимизации и комбинаторных игр.

Роберт М. Солоу пришел к выводу, что математическая экономика является основной « инфраструктурой » современной экономики:

Экономика больше не является подходящей темой для разговора между дамами и господами. Это стало технической темой. Как и любой технический предмет, он привлекает людей, которых больше интересует техника, чем предмет. Это очень плохо, но это может быть неизбежно. В любом случае, не обманывайте себя: техническое ядро ​​экономики — это необходимая инфраструктура политической экономии. Вот почему, если вы обратитесь к [справочному материалу по современной экономике] в поисках информации о современном мире, вас приведут к технической экономике, или истории, или вообще ни к чему.

Экономисты-математики

Выдающиеся экономисты-математики включают следующее.

19 век

• Энрико Бароне
• Антуан Огюстен Курно
• Фрэнсис Исидро Эджворт

• Ирвинг Фишер
• Уильям Стэнли Джевонс

• Вильфредо Парето
• Леон Вальрас

20 век

• Хараламбос Д. Алипрантис
• РГД Аллен
• Морис Алле
• Кеннет Дж. Эрроу
• Роберт Дж. Ауманн
• Ив Баласко
• Дэвид Блэквелл
• Лоуренс Э. Блюм
• Грасиела Чичилниски
• Джордж Б. Данциг
• Жерар Дебре
• Марио Драги
• Жак Х. Дрез
• Дэвид Гейл
• Николас Джорджеску-Роген

• Роджер Геснери
• Фрэнк Хан
• Джон К. Харсаньи
• Джон Р. Хикс
• Вернер Хильденбранд
• Гарольд Хотеллинг
• Леонид Гурвич
• Леонид Канторович
• Тьяллинг Купманс
• Дэвид М. Крепс
• Гарольд В. Кун
• Эдмон Малинво
• Андреу Мас-Колелл
• Эрик Маскин

• Нимрод Мегиддо
• Жан-Франсуа Мертенс
• Джеймс Миррлис
• Роджер Майерсон
• Джон Форбс Нэш-младший
• Джон фон Нейман
• Эдвард С. Прескотт
• Рой Рэднер
• Фрэнк Рэмси
• Дональд Джон Робертс
• Пол Самуэльсон
• Yuliy Sannikov
• Томас Сарджент
• Леонард Дж. Сэвидж
• Герберт Шарф

• Райнхард Зельтен
• Амартья Сен
• Ллойд С. Шепли
• Стивен Смейл
• Роберт Солоу
• Хьюго Ф. Саншайн
• Нэнси Л. Стоки
• Альберт В. Такер
• Хирофуми Удзава
• Роберт Б. Уилсон
• Авраам Вальд
• Герман Вольд
• Николас К. Яннелис

См. также

• Эконофизика
• Математические финансы

Дальнейшее чтение

• Альфа К. Чанг и Кевин Уэйнрайт, [1967] 2005. Фундаментальные методы математической экономики , МакГроу-Хилл Ирвин. Содержание.
• Э. Рой Вайнтрауб , 1982. Математика для экономистов , Кембридж. Содержание .
• Стивен Глейстер , 1984. Математические методы для экономистов , 3-е изд., Блэквелл. Содержание.
• Акира Такаяма, 1985. Математическая экономика , 2-е изд. Кембридж. Содержание .
• Нэнси Л. Стоки и Роберт Э. Лукас с Эдвардом Прескоттом , 1989. Рекурсивные методы в экономической динамике , издательство Гарвардского университета. на описание и просмотр глав Ссылки .
• А. К. Диксит , [1976] 1990. Оптимизация в экономической теории , 2-е изд., Оксфорд. Описание и предварительный просмотр содержимого .
• Кеннет Л. Джадд , 1998. Численные методы в экономике , MIT Press. на описание и просмотр глав Ссылки .
• Майкл Картер, 2001. Основы математической экономики , MIT Press. Содержание .
• Ференц Сидаровски и Шандор Молнар, 2002. Введение в теорию матриц: с приложениями к бизнесу и экономике , World Scientific Publishing. Описание и предварительный просмотр .
• Д. Уэйд Хэндс, 2004. Вводная математическая экономика , 2-е изд. Оксфорд. Содержание .
• Джанкарло Гандольфо, [1997] 2009. Экономическая динамика , 4-е изд., Springer. Описание и предварительный просмотр .
• Джон Стачурски, 2009. Экономическая динамика: теория и вычисления , MIT Press. Описание и предварительный просмотр .

Внешние ссылки

• журнала математической экономики Цели и сфера применения
• Математическая экономика и финансовая математика в Керли
• Магистр Erasmus Mundus QEM - Модели и методы количественной экономики , Модели и методы количественной экономики - QEM