Множитель Лагранжа
В математической оптимизации метод множителей Лагранжа представляет собой стратегию поиска локальных максимумов и минимумов функции , подчиненной ограничениям уравнения (т. е. при условии, что одно или несколько уравнений должны точно удовлетворяться выбранными значениями переменных ). ). [1] Он назван в честь математика Жозефа-Луи Лагранжа .
Резюме и обоснование [ править ]
Основная идея состоит в том, чтобы преобразовать задачу с ограничениями в такую форму, в которой по-прежнему можно будет применять тест производной задачи без ограничений. Связь между градиентом функции и градиентами ограничений вполне естественно приводит к переформулировке исходной задачи, известной как функция Лагранжа или лагранжиан. [2] В общем случае лагранжиан определяется как
В простых случаях, когда внутренний продукт определяется как скалярное произведение , лагранжиан равен
Метод можно резюмировать следующим образом: чтобы найти максимум или минимум функции подчиняется ограничению равенства , найдите стационарные точки рассматривать как функцию и множитель Лагранжа . Это означает, что все частные производные должны быть равны нулю, включая частную производную по . [3]
или эквивалентно
Решение, соответствующее исходной оптимизации с ограничениями, всегда является седловой точкой функции Лагранжа: [4] [5] которые можно выделить среди стационарных точек по определенности окаймленной матрицы Гессе . [6]
Большим преимуществом этого метода является то, что он позволяет решать оптимизацию без явной параметризации ограничений. В результате метод множителей Лагранжа широко используется для решения сложных задач оптимизации с ограничениями. Далее метод множителей Лагранжа обобщается условиями Каруша–Куна–Таккера , которые также могут учитывать ограничения-неравенства вида для заданной константы .
Заявление [ править ]
Следующее утверждение известно как теорема о множителе Лагранжа. [7]
Позволять быть целевой функцией, быть функцией ограничений, обе принадлежащие (то есть иметь непрерывные первые производные). Позволять — оптимальное решение следующей задачи оптимизации такое, что для матрицы частных производных , :
Тогда существует единственный множитель Лагранжа такой, что (Обратите внимание, что это несколько традиционная вещь, когда явно рассматривается как вектор-столбец, чтобы гарантировать совпадение размеров. Но с таким же успехом мы могли бы сделать это просто вектором-строкой, не прибегая к транспонированию).
Теорема о множителе Лагранжа утверждает, что в любом локальном максимуме (или минимуме) функции, оцениваемой при ограничениях равенства, если применяется квалификация ограничения (поясняется ниже), то градиент функции (в этой точке) может быть выражен как линейная комбинация градиентов ограничений (в этой точке), при этом множители Лагранжа действуют как коэффициенты . [8] Это эквивалентно утверждению, что любое направление, перпендикулярное всем градиентам ограничений, также перпендикулярно градиенту функции. Или еще сказать, что по направлению производная функции равна 0 во всех возможных направлениях.
Единственное ограничение [ править ]
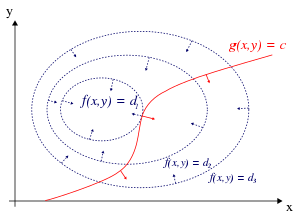
Для случая только одного ограничения и только двух переменных выбора (как показано на рисунке 1) рассмотрим задачу оптимизации
Метод множителей Лагранжа основан на интуитивном понимании того, что в максимуме f ( x , y ) не может увеличиваться в направлении любой такой соседней точки, которая также имеет g = 0 . Если бы это было так, мы могли бы идти по g = 0 , чтобы подняться выше, а это означало бы, что отправная точка на самом деле не была максимальной. С этой точки зрения, это точный аналог проверки того, равна ли производная неограниченной функции 0 , то есть мы проверяем, что производная по направлению равна 0 в любом соответствующем (жизнеспособном) направлении.
Мы можем визуализировать контуры f , заданные как f ( x , y ) = d для различных значений d , и контур g , заданный g ( x , y ) = c .
Предположим, мы идем по контурной линии с g = c . Нас интересует поиск точек, в которых f почти не меняется при ходьбе, поскольку эти точки могут быть максимумами.
Это может произойти двумя способами:
- Мы могли бы прикоснуться к контурной линии f , поскольку по определению f не меняется, когда мы идем по ее контурным линиям. Это означало бы, что касательные к контурным линиям f и g здесь параллельны.
- Мы достигли «ровной» части f , что означает, что f не меняется ни в каком направлении.
Чтобы проверить первую возможность (мы касаемся контурной линии f ), обратите внимание, что, поскольку градиент функции перпендикулярен контурным линиям, касательные к контурным линиям f и g параллельны тогда и только тогда, когда градиенты f и g параллельны. Таким образом, нам нужны точки ( x , y ) , где g ( x , y ) = c и
где
Обратите внимание, что этот метод также решает вторую возможность, что f является уровнем: если f является уровнем, то его градиент равен нулю, и установка является решением независимо от .
Чтобы объединить эти условия в одно уравнение, введем вспомогательную функцию
Обратите внимание, что это равносильно решению трех уравнений с тремя неизвестными. Это метод множителей Лагранжа.
Обратите внимание, что подразумевает как частная производная относительно является
Подводя итог
Метод легко обобщается на функции переменные
Ограниченные экстремумы f являются критическими точками лагранжиана , но они не обязательно являются локальными экстремумами (см. § Пример 2 ниже).
Можно переформулировать лагранжиан как гамильтониан , и в этом случае решения являются локальными минимумами для гамильтониана. Это сделано в теории оптимального управления в форме принципа минимума Понтрягина .
Тот факт, что решения метода множителей Лагранжа не обязательно являются экстремумами лагранжиана, также создает трудности для численной оптимизации. Эту проблему можно решить, минимизировав величину градиента лагранжиана, поскольку эти минимумы совпадают с нулями величины, как показано в Примере 5: Численная оптимизация .
Множественные ограничения [ править ]


Метод множителей Лагранжа можно расширить для решения задач с несколькими ограничениями, используя аналогичный аргумент. Рассмотрим параболоид , на который наложены два ограничения на линии, пересекающиеся в одной точке. Поскольку это единственное возможное решение, эта точка, очевидно, является ограниченным экстремумом. Однако набора уровень явно не параллелен ни одному из ограничений в точке пересечения (см. рисунок 3); вместо этого это линейная комбинация градиентов двух ограничений. В случае множественных ограничений именно это мы и ищем в целом: метод Лагранжа ищет точки, не в которых градиент обязательно кратно градиенту любого отдельного ограничения, но в котором оно представляет собой линейную комбинацию градиентов всех ограничений.
Конкретно, предположим, что у нас есть ограничений и движемся по множеству точек, удовлетворяющих Каждая точка на контуре заданной ограничительной функции имеет пространство допустимых направлений: пространство векторов, перпендикулярных Таким образом, набор направлений, разрешенных всеми ограничениями, представляет собой пространство направлений, перпендикулярных всем градиентам ограничений. Обозначим это пространство допустимых ходов через и обозначим диапазон градиентов ограничений через Затем пространство векторов, перпендикулярных каждому элементу
Нас по-прежнему интересует поиск точек, где не меняется по мере нашего продвижения, поскольку эти точки могут быть (ограниченными) экстремумами. Поэтому мы ищем так, что любое допустимое направление движения в сторону от перпендикулярен (иначе мы могли бы увеличить двигаясь в этом допустимом направлении). Другими словами, Таким образом, существуют скаляры такой, что
Эти скаляры являются множителями Лагранжа. Теперь у нас есть из них по одному на каждое ограничение.
Как и раньше, введем вспомогательную функцию
Допущение квалификации ограничения при наличии нескольких ограничений заключается в том, что градиенты ограничений в соответствующей точке линейно независимы.
формулировка с помощью дифференцируемых многообразий Современная
Задачу поиска локальных максимумов и минимумов с учетом ограничений можно обобщить до поиска локальных максимумов и минимумов на дифференцируемом многообразии. [14] В дальнейшем не обязательно, чтобы быть евклидовым пространством или даже римановым многообразием. Все проявления градиента (который зависит от выбора римановой метрики) можно заменить внешней производной
Единственное ограничение [ править ]
Позволять быть гладким многообразием размерности Предположим, что мы хотим найти стационарные точки гладкой функции при ограничении подмногообразия определяется где — гладкая функция, для которой 0 — регулярное значение .
Позволять и быть внешними производными от и . Стационарность для ограничения в означает Аналогично, ядро содержит Другими словами, и являются пропорциональными 1-формами. Для этого необходимо и достаточно, чтобы следующая система уравнения имеют место:
В этой формулировке нет необходимости явно находить множитель Лагранжа, число такой, что
Множественные ограничения [ править ]
Позволять и быть таким же, как в приведенном выше разделе в отношении случая одного ограничения. Вместо функции описано там, теперь рассмотрим гладкую функцию с функциями компонентов для чего это обычное значение . Позволять быть подмногообразием определяется
является стационарной точкой тогда и только тогда, когда содержит Для удобства пусть и где обозначает касательное отображение или якобиан Подпространство имеет размерность меньшую, чем у , а именно и принадлежит тогда и только тогда, когда принадлежит образу С вычислительной точки зрения условие состоит в том, что принадлежит пространству строк матрицы или, что эквивалентно, пространство столбцов матрицы (транспонирование). Если обозначает внешнее произведение столбцов матрицы стационарное состояние для в становится
множителей Интерпретация Лагранжа
В этом разделе мы модифицируем уравнения ограничений в виде в форму где — m вещественных констант, которые считаются дополнительными аргументами выражения Лагранжа .
Часто множители Лагранжа интерпретируются как некоторая процентная величина. Например, параметризовав контурную линию ограничения, то есть, если выражение Лагранжа равно
Итак, λ k — скорость изменения оптимизируемой величины в зависимости от параметра ограничения.Например, в лагранжевой механике уравнения движения выводятся путем нахождения стационарных точек действия , интеграла по времени от разницы между кинетической и потенциальной энергией. Таким образом, силу, действующую на частицу вследствие скалярного потенциала, F = −∇ V , можно интерпретировать как множитель Лагранжа, определяющий изменение действия (переход потенциала в кинетическую энергию) после изменения ограниченной траектории частицы. В теории управления это формулируется вместо этого как уравнения стоимости .
Более того, согласно теореме о конверте оптимальное значение множителя Лагранжа интерпретируется как предельное влияние соответствующей константы ограничения на оптимально достижимое значение исходной целевой функции: Если мы обозначим оптимальные значения звездочкой ( ), то можно показать, что
Например, в экономике оптимальная прибыль игрока рассчитывается при условии ограниченного пространства действий, где множитель Лагранжа — это изменение оптимального значения целевой функции (прибыли) вследствие ослабления заданного ограничения (например, за счет изменение дохода); в таком контексте — это предельная стоимость ограничения, называемая теневой ценой . [15]
Достаточные условия [ править ]
Достаточные условия для ограниченного локального максимума или минимума могут быть сформулированы в терминах последовательности главных миноров (определителей выровненных в верхнем левом углу подматриц) граничной матрицы Гессе вторых производных выражения Лагранжа. [6] [16]
Примеры [ править ]
Пример 1 [ править ]

Предположим, мы хотим максимизировать с учетом ограничения является Допустимым множеством единичный круг, а множествами уровня f являются диагональные линии (с наклоном −1), поэтому мы можем видеть графически, что максимум возникает при и что минимум происходит при
Для метода множителей Лагранжа ограничение имеет вид
Теперь мы можем рассчитать градиент:
Обратите внимание, что последнее уравнение является исходным ограничением.
Первые два уравнения дают
Оценка целевой функции f в этих точках дает
Таким образом, ограниченный максимум равен и ограниченный минимум равен .
Пример 2 [ править ]

Теперь мы модифицируем целевую функцию примера 1 так, чтобы минимизировать вместо снова по кругу Теперь наборы уровней по-прежнему являются линиями наклона −1, а точки на окружности, касающиеся этих наборов уровней, снова становятся и Эти точки касания являются максимумами
С другой стороны, минимумы происходят на уровне, установленном для (поскольку по своей конструкции не может принимать отрицательные значения), при и где кривые уровня не касаются ограничения. Условие, которое правильно определяет все четыре точки как экстремумы; минимумы характеризуются и максимумы по
Пример 3 [ править ]

В этом примере рассматриваются более сложные вычисления, но это по-прежнему проблема с одним ограничением.
Предположим, кто-то хочет найти максимальные значения
Поскольку существует только одно ограничение, существует один множитель, скажем
Ограничение тождественно равен нулю на окружности радиуса Любое кратное может быть добавлен в уход неизменным в интересующей области (на круге, где выполняется наше исходное ограничение).
Применение обычного метода множителей Лагранжа дает
Оценивая цель в этих точках, можно обнаружить, что
Следовательно, целевая функция достигает глобального максимума (с учетом ограничений) при и глобальный минимум в Суть представляет собой локальный минимум и является локальным максимумом что можно определить путем рассмотрения Гессе матрицы
Обратите внимание, что пока является критической точкой это не локальный экстремум У нас есть
Учитывая любую окрестность можно выбрать небольшой позитив и маленький любого знака, чтобы получить значения как больше, так и меньше Это также можно увидеть из матрицы Гессе оценивается в этой точке (или даже в любой из критических точек), которая представляет собой неопределенную матрицу . Каждая из критических точек является седловой точкой [4]
Пример 4 – Энтропия [ править ]
Предположим, мы хотим найти дискретное распределение вероятностей в точках с максимальной информационной энтропией . Это то же самое, что сказать, что мы хотим найти наименее структурированное распределение вероятностей в точках Другими словами, мы хотим максимизировать уравнение энтропии Шеннона :
Чтобы это было распределение вероятностей, сумма вероятностей в каждой точке должно равняться 1, поэтому наше ограничение:
Мы используем множители Лагранжа, чтобы найти точку максимальной энтропии: по всем дискретным распределениям вероятностей на Мы требуем, чтобы:
Проведя дифференцирование этих n уравнений, получим
Это показывает, что все равны (так как зависят только от λ ). Используя ограничение
Следовательно, равномерное распределение — это распределение с наибольшей энтропией среди распределений по n точкам.
Пример 5 – Численная оптимизация [ править ]

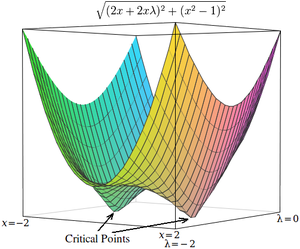
Критические точки лагранжиана возникают в седловых точках , а не в локальных максимумах (или минимумах). [4] [17] К сожалению, многие методы численной оптимизации, такие как восхождение на холм , градиентный спуск , некоторые квазиньютоновские методы и другие, предназначены для поиска локальных максимумов (или минимумов), а не седловых точек. По этой причине необходимо либо изменить формулировку, чтобы гарантировать, что это задача минимизации (например, путем экстремизации квадрата градиента лагранжиана , как показано ниже), либо использовать метод оптимизации, который находит стационарные точки (например, метод Ньютона без экстремума поиск строки ) и не обязательно экстремумов.
В качестве простого примера рассмотрим задачу нахождения значения x , которое минимизирует ограничено так, что (Эта проблема несколько нетипична, поскольку этому ограничению удовлетворяют только два значения, но она полезна для иллюстративных целей, поскольку соответствующую функцию без ограничений можно визуализировать в трех измерениях.)
Используя множители Лагранжа, эту задачу можно преобразовать в задачу неограниченной оптимизации:
Две критические точки возникают в седловых точках, где x = 1 и x = −1 .
Чтобы решить эту проблему с помощью метода численной оптимизации, мы должны сначала преобразовать эту проблему так, чтобы критические точки находились в локальных минимумах. Это делается путем вычисления величины градиента задачи неограниченной оптимизации.
Сначала мы вычисляем частную производную задачи без ограничений по каждой переменной:
Если целевая функция не является легко дифференцируемой, дифференциал по каждой переменной можно аппроксимировать как
Далее мы вычисляем величину градиента, которая представляет собой квадратный корень из суммы квадратов частных производных:
(Поскольку величина всегда неотрицательна, оптимизация по квадрату величины эквивалентна оптимизации по величине. Таким образом, «квадратный корень» можно опустить в этих уравнениях без ожидаемой разницы в результатах оптимизации.)
Критические точки h встречаются в точках x = 1 и x = −1 , как и в В отличие от критических точек однако критические точки h возникают в локальных минимумах, поэтому для их поиска можно использовать методы численной оптимизации.
Приложения [ править ]
Теория управления [ править ]
В теории оптимального управления множители Лагранжа интерпретируются как переменные стоимости , а множители Лагранжа переформулируются как минимизация гамильтониана в принципе минимума Понтрягина .
Нелинейное программирование [ править ]
Метод множителей Лагранжа имеет несколько обобщений. В нелинейном программировании существует несколько правил множителей, например правило множителей Каратеодори – Джона и правило выпуклых множителей, для ограничений-неравенств. [18]
Энергетические системы [ править ]
Методы, основанные на множителях Лагранжа, находят применение в энергосистемах , например, при размещении распределенных энергетических ресурсов (DER) и сбросе нагрузки. [19]
обучение подкреплением с Безопасное
Метод множителей Лагранжа применяется к марковским процессам принятия решений с ограничениями . [20] Естественно, он создает основанные на градиенте первичные двойственные алгоритмы в безопасном обучении с подкреплением. [21]
См. также [ править ]
- Корректировка наблюдений
- Двойственность
- Индекс Гиттинса
- Условия Каруша – Куна – Такера : обобщение метода множителей Лагранжа
- Множители Лагранжа в банаховых пространствах : еще одно обобщение метода множителей Лагранжа
- Тест множителя Лагранжа при оценке максимального правдоподобия
- Лагранжева релаксация
Ссылки [ править ]
- ^ Хоффманн, Лоуренс Д.; Брэдли, Джеральд Л. (2004). Исчисление для бизнеса, экономики, социальных и биологических наук (8-е изд.). стр. 575–588. ISBN 0-07-242432-Х .
- ^ Бивис, Брайан; Доббс, Ян М. (1990). «Статическая оптимизация» . Теория оптимизации и устойчивости для экономического анализа . Нью-Йорк: Издательство Кембриджского университета. п. 40. ИСБН 0-521-33605-8 .
- ^ Проттер, Мюррей Х .; Морри, Чарльз Б. младший. (1985). Промежуточное исчисление (2-е изд.). Нью-Йорк, штат Нью-Йорк: Спрингер. п. 267. ИСБН 0-387-96058-9 .
- ^ Jump up to: Перейти обратно: а б с Уолш, Г. Р. (1975). «Свойство перевала функции Лагранжа» . Методы оптимизации . Нью-Йорк, штат Нью-Йорк: Джон Уайли и сыновья. стр. 39–44. ISBN 0-471-91922-5 .
- ^ Кальман, Дэн (2009). «Выравнивание с помощью Лагранжа: альтернативный взгляд на оптимизацию с ограничениями». Журнал «Математика» . 82 (3): 186–196. дои : 10.1080/0025570X.2009.11953617 . JSTOR 27765899 . S2CID 121070192 .
- ^ Jump up to: Перейти обратно: а б Зильберберг, Юджин; Суен, Винг (2001). Структура экономики: математический анализ (Третье изд.). Бостон: Ирвин МакГроу-Хилл. стр. 134–141. ISBN 0-07-234352-4 .
- ^ де ла Фуэнте , Анхель (2000). Математические методы и модели для экономистов . Кембридж: Издательство Кембриджского университета. п. 285 . дои : 10.1017/CBO9780511810756 . ISBN 978-0-521-58512-5 .
- ^ Люенбергер, Дэвид Г. (1969). Оптимизация методами векторного пространства . Нью-Йорк: Джон Уайли и сыновья. стр. 188–189.
- ^ Берцекас, Дмитрий П. (1999). Нелинейное программирование (Второе изд.). Кембридж, Массачусетс: Athena Scientific. ISBN 1-886529-00-0 .
- ^ Вапнярский, И.Б. (2001) [1994], «Множители Лагранжа» , Энциклопедия математики , EMS Press .
- ^ Ласдон, Леон С. (2002) [1970]. Теория оптимизации для больших систем (переиздание). Минеола, Нью-Йорк, Нью-Йорк: Дувр. ISBN 0-486-41999-1 . МР 1888251 .
- ^ Хириар-Уррути, Жан-Батист; Лемарешаль, Клод (1993). «Глава XII: Абстрактная двойственность для практиков». Алгоритмы выпуклого анализа и минимизации . Фундаментальные принципы математических наук. Том 306. Берлин, Германия: Springer-Verlag. стр. 136–193 (и библиографические комментарии, стр. 334–335). ISBN 3-540-56852-2 . МР 1295240 . Том II: Расширенная теория и пакетные методы.
- ^ Лемарешаль, Клод (15–19 мая 2000 г.). «Лагранжева релаксация». В Юнгере, Майкл; Наддеф, Денис (ред.). Вычислительная комбинаторная оптимизация: статьи весенней школы, проходившей в замке Дагштуль . Весенняя школа прошла в замке Дагштуль, 15–19 мая 2000 г. Конспекты лекций по информатике. Том. 2241. Берлин, Германия: Springer-Verlag (опубликовано в 2001 г.). стр. 112–156. дои : 10.1007/3-540-45586-8_4 . ISBN 3-540-42877-1 . МР 1900016 . S2CID 9048698 .
- ^ Лафонтен, Жак (2015). Введение в дифференциальные многообразия . Спрингер. п. 70. ИСБН 978-3-319-20735-3 .
- ^ Диксит, Авинаш К. (1990). «Теневые цены» . Оптимизация в экономической теории (2-е изд.). Нью-Йорк: Издательство Оксфордского университета. стр. 40–54. ISBN 0-19-877210-6 .
- ^ Чан, Альфа К. (1984). Фундаментальные методы математической экономики (Третье изд.). МакГроу-Хилл. п. 386 . ISBN 0-07-010813-7 .
- ^ Хит, Майкл Т. (2005). Научные вычисления: вводный обзор . МакГроу-Хилл. п. 203. ИСБН 978-0-07-124489-3 .
- ^ Пурсио, Брюс Х. (1980). «Современные правила мультипликатора» . Американский математический ежемесячник . 87 (6): 433–452. дои : 10.2307/2320250 . JSTOR 2320250 .
- ^ Гаутам, Мукеш; Бхусал, Нараян; Бенидрис, Мохаммед (2020). Подход, основанный на чувствительности, к адаптивному отключению нагрузки при пониженной частоте . Техасская конференция по энергетике и энергетике IEEE 2020 (TPEC). Институт инженеров электроники и электротехники . стр. 1–5. дои : 10.1109/TPEC48276.2020.9042569 .
- ^ Альтман, Эйтан (2021). Марковские процессы принятия решений с ограничениями . Рутледж .
- ^ Дин, Дуншэн; Чжан, Кайцин; Йованович, Михайло; Басар, Тамер (2020). Первично-двойственный метод градиента естественной политики для марковских процессов принятия решений с ограничениями . Достижения в области нейронных систем обработки информации.
Дальнейшее чтение [ править ]
- Бивис, Брайан; Доббс, Ян М. (1990). «Статическая оптимизация» . Теория оптимизации и устойчивости для экономического анализа . Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. стр. 32–72. ISBN 0-521-33605-8 .
- Берцекас, Дмитрий П. (1982). Оптимизация с ограничениями и методы множителей Лагранжа . Нью-Йорк, штат Нью-Йорк: Academic Press. ISBN 0-12-093480-9 .
- Беверидж, Гордон С.Г.; Шехтер, Роберт С. (1970). «Множители Лагранжа» . Оптимизация: теория и практика . Нью-Йорк, штат Нью-Йорк: МакГроу-Хилл. стр. 244–259. ISBN 0-07-005128-3 .
- Бингер, Брайан Р.; Хоффман, Элизабет (1998). «Ограниченная оптимизация». Микроэкономика с исчислением (2-е изд.). Чтение: Аддисон-Уэсли. стр. 56–91. ISBN 0-321-01225-9 .
- Картер, Майкл (2001). «Ограничения равенства» . Основы математической экономики . Кембридж, Массачусетс: MIT Press. стр. 516–549. ISBN 0-262-53192-5 .
- Хестенес, Магнус Р. (1966). «Минимумы функций, на которые распространяются ограничения равенства». Вариационное исчисление и теория оптимального управления . Нью-Йорк, штат Нью-Йорк: Уайли. стр. 29–34.
- Уайли, К. Рэй; Барретт, Луи К. (1995). «Экстремумы интегралов при ограничении». Высшая инженерная математика (Шестое изд.). Нью-Йорк, штат Нью-Йорк: МакГроу-Хилл. стр. 1096–1103. ISBN 0-07-072206-4 .
Внешние ссылки [ править ]
Экспозиция [ править ]
- Стюард. «Концептуальное введение» . slimy.com . - плюс краткое обсуждение множителей Лагранжа в вариационном исчислении , используемых в физике.
- Карпентер, Кеннет Х. «Множители Лагранжа для квадратичных форм с линейными ограничениями» (PDF) . Канзасский государственный университет .
Дополнительные текстовые и интерактивные апплеты [ править ]
- Резник. «Простое объяснение на примере того, как правительства используют налоги в качестве множителей Лагранжа» . umiacs.umd.edu . Университет Мэриленда .
- Кляйн, Дэн. «Множители Лагранжа без постоянных рубцов] Объяснение с акцентом на интуицию» (PDF) . nlp.cs.berkeley.edu . Калифорнийский университет в Беркли .
- Сатьянараяна, Шаши. «Геометрическое представление метода множителей Лагранжа» . wolfram.com ( Mathematica демонстрация ). Вольфрам Исследования .
Требуется Internet Explorer/Firefox/Safari.
— Обеспечивает убедительное представление в двух измерениях о том, что в точке минимизации направление наибольшего спуска должно быть перпендикулярно касательной кривой ограничения в этой точке. - «Множители Лагранжа – две переменные» . Открытые курсы MIT (ocw.mit.edu) (Applet). Массачусетский технологический институт .
- «Множители Лагранжа» . Открытые курсы MIT (ocw.mit.edu) (видеолекция). Математика 18-02: Многомерное исчисление. Массачусетский технологический институт . Осень 2007 года.
- Берцекас. «Подробнее о множителях Лагранжа» (PDF) . athenasc.com (слайды/лекции курса). Нелинейное программирование. — Слайды курса, сопровождающие текст по нелинейной оптимизации.
- Вятт, Джон (7 апреля 2004 г.) [19 ноября 2002 г.]. «Множители Легранжа, оптимизация с ограничениями и принцип максимальной энтропии» (PDF) . www-mtl.mit.edu . Elec E & CS / Mech E 6.050 – Информация, энтропия и вычисления. — Геометрическая идея, лежащая в основе множителей Лагранжа.
- «Использование множителей Лагранжа в оптимизации» . matlab.cheme.cmu.edu (пример MATLAB). Питтсбург, Пенсильвания: Университет Карнеги-Меллона. 24 декабря 2011 г.



















![{\displaystyle {\Bigl [}\operatorname {D} g(x_{\star }){\Bigr ]}_{j,k}={\frac {\ \partial g_{j}\ }{\partial x_ {к}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64847aaf74c536fcbdd35ff935281fda73117f3)





































































































![{\displaystyle {\begin{aligned}&{\mathcal {L}}(x_{1},x_{2},\ldots ;\lambda _{1},\lambda _{2},\ldots ;c_{ 1},c_{2},\ldots )\\[4pt]={}&f(x_{1},x_{2},\ldots )+\lambda _{1}(c_{1}-g_{1 }(x_{1},x_{2},\ldots ))+\lambda _{2}(c_{2}-g_{2}(x_{1},x_{2},\dots ))+\ cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1867ddf9118c757c322a3d5c0c94965c64a65d0a)









![{\displaystyle {\begin{aligned}{\mathcal {L}}(x,y,\lambda)&=f(x,y)+\lambda \cdot g(x,y)\\[4pt]&= x+y+\lambda (x^{2}+y^{2}-1)\ ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69623e2b0ffebabe351b9e7ed58a76751601bf66)


![{\displaystyle {\begin{aligned}\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda) &=\left({\frac {\partial {\mathcal { L}}}{\partial x}},{\frac {\partial {\mathcal {L}}}{\partial y}},{\frac {\partial {\mathcal {L}}}{\partial \ лямбда }}\right)\\[4pt]&=\left(1+2\lambda x,1+2\lambda y,x^{2}+y^{2}-1\right)\ \color { серый}{,}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf9c05227cba7a2024d2ef806cf55712c1a3073)









































































![{\displaystyle {\begin{aligned}&{\frac {\partial {\mathcal {L}}}{\partial x}}=2x+2x\lambda \\[5pt]&{\frac {\partial {\ mathcal {L}}}{\partial \lambda }}=x^{2}-1~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498e5f0200a9e684456385a4d6b121c2274c2737)
![{\displaystyle {\begin{aligned}{\frac {\ \partial {\mathcal {L}}\ }{\partial x}}\approx {\frac {{\mathcal {L}}(x+\varepsilon,\ лямбда )-{\mathcal {L}}(x,\lambda )}{\varepsilon }},\\[5pt]{\frac {\ \partial {\mathcal {L}}\ }{\partial \lambda } }\approx {\frac {{\mathcal {L}}(x,\lambda +\varepsilon )-{\mathcal {L}}(x,\lambda )}{\varepsilon }},\end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0de4bda576fdb293b9e0b1f0ebe3f93d57c84f06)

![{\displaystyle {\begin{aligned}h(x,\lambda) &={\sqrt {(2x+2x\lambda)^{2}+(x^{2}-1)^{2}\ }} \\[4pt]&\approx {\sqrt {\left({\frac {\ {\mathcal {L}}(x+\varepsilon,\lambda)-{\mathcal {L}}(x,\lambda)\ }{\varepsilon }}\right)^{2}+\left({\frac {\ {\mathcal {L}}(x,\lambda +\varepsilon )-{\mathcal {L}}(x,\ лямбда )\ }{\varepsilon }}\right)^{2}\ }}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19179451d91b7f354ff6326de2c76749c3e9f0f)

