Списки тем по математике

Списки тем по математике охватывают множество тем, связанных с математикой . Некоторые из этих списков ссылаются на сотни статей; некоторые ссылки только на некоторых. Шаблон справа содержит ссылки на алфавитные списки всех математических статей. В этой статье собран тот же контент, организованный таким образом, который лучше подходит для просмотра.Списки охватывают аспекты базовой и продвинутой математики, методологии, математических утверждений, интегралов, общих понятий, математических объектов и справочных таблиц.Они также охватывают уравнения, названные в честь людей, обществ, математиков, журналов и метасписков.

Цель этого списка не аналогична цели Классификации предметов математики, сформулированной Американским математическим обществом . Многие математические журналы просят авторов исследовательских работ и разъяснительных статей перечислять в своих статьях коды предметов из Классификации предметов математики. Перечисленные таким образом коды предметов используются двумя основными рецензирующими базами данных: Mathematical Reviews и Zentralblatt MATH . В этом списке есть некоторые элементы, которые не вписываются в такую классификацию, например список экспоненциальных тем и список факториальных и биномиальных тем , которые могут удивить читателя разнообразием их охвата.

Базовая математика [ править ]

Эту отрасль обычно преподают в средней школе или на первом курсе университета.

Области высшей математики [ править ]

В качестве приблизительного ориентира этот список разделен на чистые и прикладные разделы, хотя на самом деле эти ветви пересекаются и переплетаются.

Чистая математика [ править ]

Алгебра [ править ]

Алгебра включает изучение алгебраических структур, которые представляют собой множества и операции, определенные на этих множествах и удовлетворяющие определенным аксиомам. Область алгебры далее делится в зависимости от того, какая структура изучается; например, теория групп касается алгебраической структуры, называемой группой .

Исчисление и анализ [ править ]

Исчисление изучает вычисление пределов, производных и интегралов функций действительных чисел и, в частности, изучает мгновенные скорости изменения. Анализ развился из исчисления.

Геометрия и топология [ править ]

Геометрия изначально представляет собой изучение пространственных фигур, таких как круги и кубы, хотя она была значительно обобщена. Топология, разработанная на основе геометрии; он рассматривает те свойства, которые не меняются, даже когда фигуры деформируются путем растяжения и изгиба, например, размерность.

Комбинаторика [ править ]

Комбинаторика занимается изучением дискретных (и обычно конечных ) объектов. Аспекты включают «подсчет» объектов, удовлетворяющих определенным критериям ( перечислительная комбинаторика ), принятие решения о том, когда критерии могут быть выполнены, а также построение и анализ объектов, отвечающих критериям (как в комбинаторных проектах и матроидов теории ), поиск «самых больших», «наименьших», или «оптимальные» объекты ( экстремальная комбинаторика и комбинаторная оптимизация ) и нахождение алгебраических структур, которые могут иметь эти объекты ( алгебраическая комбинаторика ).

Логика [ править ]

Логика — это основа, лежащая в основе математической логики и всей остальной математики. Он пытается формализовать действительные рассуждения. В частности, он пытается определить, что представляет собой доказательство.

Теория чисел [ править ]

Раздел математики занимается свойствами и отношениями чисел, особенно положительных целых чисел. Теория чисел — это раздел чистой математики, посвященный в основном изучению целых чисел и целочисленных функций. Немецкий математик Карл Фридрих Гаусс сказал: «Математика — царица наук, а теория чисел — царица математики».Теория чисел также изучает натуральные или целые числа. Одним из центральных понятий теории чисел является понятие простого числа , и существует множество вопросов о простых числах, которые кажутся простыми, но решение которых продолжает ускользать от математиков.

Список тем по теории алгебраических чисел
Список тем по теории чисел
Список развлекательных тем по теории чисел
Словарь арифметики и диофантовой геометрии
Список простых чисел — не просто таблица, а список различных видов простых чисел (каждое с сопроводительной таблицей).
Список дзета-функций

Прикладная математика [ править ]

и дифференциальные уравнения Динамические системы

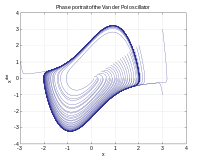
Фазовый портрет динамической системы с непрерывным временем — генератора Ван дер Поля .

Дифференциальное уравнение – это уравнение, содержащее неизвестную функцию и ее производные.

В динамической системе фиксированное правило описывает зависимость точки геометрического пространства от времени. Математические модели, используемые для описания качания маятника часов, течения воды в трубе или количества рыбы каждую весну в озере, являются примерами динамических систем.

Математическая физика [ править ]

Математическая физика занимается «применением математики к физическим задачам и разработкой математических методов, подходящих для таких приложений и для формулирования физических теорий». ¹

Теория вычислений [ править ]

Области математики и информатики пересекаются как в информатике , изучении алгоритмов и структур данных, так и в научных вычислениях , изучении алгоритмических методов решения задач в математике, естественных науках и технике.

Теория информации и обработка сигналов [ править ]

Теория информации — это раздел прикладной математики и социальных наук, занимающийся количественной оценкой информации . Исторически теория информации была разработана для обнаружения фундаментальных ограничений на сжатие и надежную передачу данных.

Обработка сигналов — это анализ, интерпретация и манипулирование сигналами . Сигналы, представляющие интерес, включают звук , изображения , биологические сигналы, такие как ЭКГ , сигналы радара и многие другие. Обработка таких сигналов включает в себя фильтрацию , хранение и реконструкцию, отделение информации от шума , сжатие и извлечение признаков .

Вероятность и статистика [ править ]

Теория вероятностей — это формализация и изучение математики неопределенных событий или знаний. Смежная область математической статистики развивает статистическую теорию вместе с математикой. Статистика , наука, занимающаяся сбором и анализом данных, является автономной дисциплиной (а не подразделом прикладной математики ).

Теория игр [ править ]

Теория игр — это раздел математики , который использует модели для изучения взаимодействия с формализованными структурами стимулов («играми»). Он имеет применение в различных областях, включая экономику , антропологию , политологию , социальную психологию и военную стратегию .

Исследование операций [ править ]

Исследование операций — это изучение и использование математических моделей, статистики и алгоритмов для помощи в принятии решений, обычно с целью улучшения или оптимизации производительности реальных систем.

Методология [ править ]

Математические утверждения [ править ]

Математическое утверждение представляет собой предложение или утверждение некоторого математического факта, формулы или конструкции. К таким утверждениям относятся аксиомы и теоремы, которые можно доказать на их основе, гипотезы, которые могут быть недоказанными или даже недоказуемыми, а также алгоритмы вычисления ответов на вопросы, которые можно выразить математически.

Общие понятия [ править ]

Математические объекты [ править ]

Среди математических объектов — числа, функции, множества, множество вещей, называемых « пространствами » того или иного рода, алгебраические структуры, такие как кольца, группы или поля, и многое другое.

названные в честь людей , Уравнения

Научные уравнения, названные в честь людей

О математике [ править ]

Математики [ править ]

Математики изучают и исследуют все различные области математики. Публикация новых открытий в математике продолжается огромными темпами в сотнях научных журналов, многие из которых посвящены математике, а многие посвящены предметам, к которым математика применяется (таким как теоретическая информатика и теоретическая физика ).

Работы отдельных математиков [ править ]

Справочные таблицы [ править ]

Интегралы [ править ]

В исчислении интеграл функции представляет собой обобщение площади, массы, объема, суммы и суммы. На следующих страницах перечислены интегралы от множества различных функций.

Журналы [ править ]

Мета-списки [ править ]

См. также [ править ]

Другие [ править ]

Примечания [ править ]

^ Примечание 1 : Определение из журнала математической физики [1] .

Внешние ссылки и ссылки [ править ]

Классификация предметов математики 2000 г. от Американского математического общества . Авторы схем обнаруживают, что многие журналы математических исследований просят их использовать их для классификации своих материалов; опубликованные затем включают эти классификации.
Математический атлас
Математическая формула

связанных с математикой В эту статью включен список списков, .

v т и Основные математики области
History Timeline Future Lists Glossary
Foundations	Category theory Information theory Mathematical logic Philosophy of mathematics Set theory Type theory
Algebra	Abstract Commutative Elementary Group theory Linear Multilinear Universal Homological
Analysis	Calculus Real analysis Complex analysis Hypercomplex analysis Differential equations Functional analysis Harmonic analysis Measure theory
Discrete	Combinatorics Graph theory Order theory
Geometry	Algebraic Analytic Arithmetic Differential Discrete Euclidean Finite
Number theory	Arithmetic Algebraic number theory Analytic number theory Diophantine geometry
Topology	General Algebraic Differential Geometric Homotopy theory
Applied	Engineering mathematics Mathematical biology Mathematical chemistry Mathematical economics Mathematical finance Mathematical physics Mathematical psychology Mathematical sociology Mathematical statistics Probability Statistics Systems science Control theory Game theory Operations research
Computational	Computer science Theory of computation Computational complexity theory Numerical analysis Optimization Computer algebra
Related topics	Mathematicians lists Informal mathematics Films about mathematicians Recreational mathematics Mathematics and art Mathematics education
Mathematics portal Category Commons WikiProject