Список моментов инерции
Момент инерции , обозначаемый I , измеряет степень, в которой объект сопротивляется вращательному ускорению вокруг определенной оси . Это вращательный аналог массы (которая определяет сопротивление объекта линейному ускорению ). Моменты инерции массы имеют единицы измерения . ML 2 ([масса] × [длина] 2 ). Его не следует путать со вторым моментом площади , который имеет единицы измерения L. 4 ([длина] 4 ) и используется в расчетах балок. Момент инерции массы часто также называют инерцией вращения , а иногда и угловой массой .
Для простых объектов с геометрической симметрией часто можно определить момент инерции в точном выражении в замкнутой форме . Обычно это происходит, когда плотность массы постоянна, но в некоторых случаях плотность может меняться и по всему объекту. В общем, может быть непросто символически выразить момент инерции форм с более сложным распределением массы и отсутствием симметрии. При расчете моментов инерции полезно помнить, что это аддитивная функция, и использовать параллельной и теоремы о перпендикулярной оси .
В этой статье в основном рассматриваются симметричные распределения массы с постоянной плотностью по всему объекту, а ось вращения проходит через центр масс, если не указано иное.
Моменты инерции [ править ]
Ниже приведены скалярные моменты инерции. В общем случае момент инерции представляет собой тензор , см. ниже.
| Описание | Фигура | Момент(ы) инерции |
|---|---|---|
| Точка массы М на расстоянии г от оси вращения. Точечная масса не имеет момента инерции вокруг своей оси, но с помощью теоремы о параллельности оси достигается момент инерции вокруг удаленной оси вращения. | 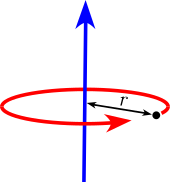 | |
| Две точечные массы, m 1 и m 2 , с приведенной массой µ и разделенные расстоянием x вокруг оси, проходящей через центр масс системы и перпендикулярной линии, соединяющей две частицы. |  | |
| Тонкий стержень длиной L и массой m , перпендикулярный оси вращения, вращающийся вокруг своего центра. Это выражение предполагает, что стержень представляет собой бесконечно тонкую (но жесткую) проволоку. Это частный случай тонкой прямоугольной пластины с осью вращения в центре пластины, с w = L и h = 0. | 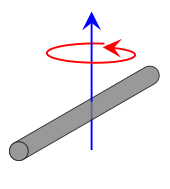 | [1] |
| Тонкий стержень длиной L и массой m , перпендикулярный оси вращения, вращающийся вокруг одного конца. Это выражение предполагает, что стержень представляет собой бесконечно тонкую (но жесткую) проволоку. Это также частный случай тонкой прямоугольной пластины с осью вращения на конце пластины, с h = L и w = 0. |  | [1] |
| Тонкая круглая петля радиуса r и массы m . Это частный случай тора при a = 0 (см. ниже), а также толстостенной цилиндрической трубки с открытыми концами при r 1 = r 2 и h = 0. |  | |
| Тонкий твердый диск радиуса r и массы m . Это частный случай сплошного цилиндра с h = 0. Это является следствием теоремы о перпендикулярной оси . | 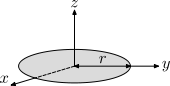 | |
| Однородное кольцо (диск с концентрическим отверстием) массы m , внутреннего радиуса r 1 и внешнего радиуса r 2. | 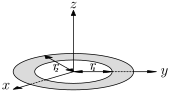 | |
| Кольцевое пространство с постоянной плотностью площади | ||
| Тонкая цилиндрическая оболочка с открытыми концами радиуса r и массы m . Это выражение предполагает, что толщина оболочки незначительна. Это частный случай толстостенной цилиндрической трубы при r 1 = r 2 .Кроме того, точечная масса m на конце стержня длиной r имеет тот же момент инерции, и значение r называется радиусом вращения . |  | [1] |
| Сплошной цилиндр радиуса r , высоты h и массы m . Это частный случай толстостенной цилиндрической трубы с r 1 = 0. |  | [1] |
| Толстостенная цилиндрическая трубка с открытыми концами внутреннего радиуса r 1 , внешнего радиуса r 2 , длины h и массы m . |  | [1] [2] |
| С плотностью ρ и той же геометрией | ||
| Правильный тетраэдр со стороной s и массой m с осью вращения, проходящей через вершину тетраэдра и его центр масс. |  | |
| Правильный октаэдр со стороной s и массой m |  | [3] [3] |
| Правильный додекаэдр со стороной s и массой m | (где ) [3] | |
| Правильный икосаэдр со стороной s и массой m. | ||
| Полая сфера радиуса r и массы m . |  | [1] |
| Твердая сфера (шар) радиуса r и массы m . |  | [1] |
| Сфера (оболочка) радиуса r 2 и массы m с центрированной сферической полостью радиуса r 1 . Когда радиус полости r 1 = 0, объект представляет собой сплошной шар (вверху). Когда r 1 = r 2 , , а объект представляет собой полую сферу. | 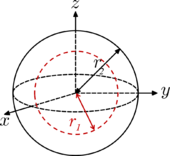 | [1] |
| Прямой круглый конус радиусом r , высотой h и массой m. |  | [4] Об оси, проходящей через наконечник: |
| Прямой круглый полый конус радиусом r , высотой h и массой m. |  | [4] [4] |
| Тор с малым радиусом a , большим радиусом b и массой m . |  | Вокруг оси, проходящей через центр и перпендикулярной диаметру: [5] О диаметре: [5] |
| Эллипсоид (сплошной) полуосей a , b и c массой m |  | [6] |
| Тонкая прямоугольная пластина высотой h , шириной w и массой m. (Ось вращения на конце пластины) | 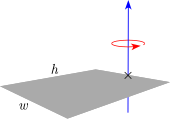 | |
| Тонкая прямоугольная пластина высотой h , шириной w и массой m. (Ось вращения в центре) |  | [1] |
| Тонкая прямоугольная пластина массы m, длина стороны, прилегающей к стороне, содержащей ось вращения, равна r. [а] (Ось вращения вдоль боковой стороны пластины) | ||
| Твердый прямоугольный кубоид высотой h , шириной w , глубиной d и массой m . [7] Для одинаково ориентированного куба со сторонами длиной , |  | |
| Твердый кубоид высотой D , шириной W и длиной L и массой m , вращающийся вокруг самой длинной диагонали. Для куба с гранями , . |  | |
| Наклоненный сплошной кубоид глубины d , ширины w и длины l и массы m , вращающийся вокруг вертикальной оси (ось y, как показано на рисунке). Для куба с гранями , . | 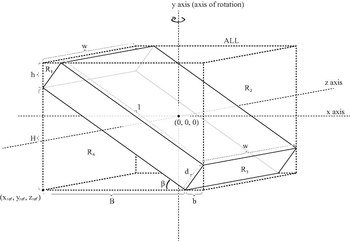 | [8] |
| Треугольник с вершинами в начале координат, а также в точках P и Q , с массой m , вращающийся вокруг оси, перпендикулярной плоскости и проходящей через начало координат. | ||
| Плоский многоугольник с вершинами P 1 , P 2 , P 3 , ..., P N и массой m, равномерно распределенными внутри него, вращающийся вокруг оси, перпендикулярной плоскости и проходящей через начало координат. | 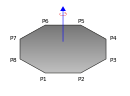 | |
| Плоский правильный многоугольник с n -вершинами и массой m, равномерно распределенными внутри, вращающийся вокруг оси, перпендикулярной плоскости и проходящей через ее барицентр . R — радиус описанной окружности . | [9] | |
| Равнобедренный треугольник массы M , угла при вершине 2β и длины общей стороны L (ось, проходящая через вершину, перпендикулярно плоскости) |  | [9] |
| Бесконечный диск с массой, распределенной в двумерном гауссовском распределении по двум осям вокруг оси вращения, с плотностью массы как функцией вектора положения. | 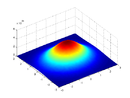 |
Список 3D тензоров инерции [ править ]
Этот список тензоров момента инерции приведен для главных осей каждого объекта.
Чтобы получить скалярные моменты инерции I, приведенные выше, тензорный момент инерции I проецируется вдоль некоторой оси, определяемой единичным вектором n, согласно формуле:
где точки указывают на сокращение тензора и соглашение Эйнштейна о суммировании используется . В приведенной выше таблице n будет единичным декартовым базисом ex e , e y , z y для получения I x , I z , I соответственно .
| Описание | Фигура | Тензор момента инерции |
|---|---|---|
| Твердая сфера радиуса r и массы m | 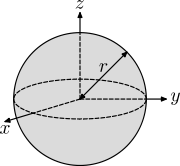 | |
| Полая сфера радиуса r и массы m |  | |
| Твердый эллипсоид полуосей a , b , c и массы m |  | |
| Прямой круглый конус радиусом r , высотой h и массой m около вершины. | 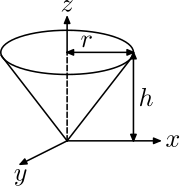 | |
| Твердый кубоид шириной w , высотой h , глубиной d и массой m. |  | |
| Тонкий стержень вдоль оси Y длиной l и массой m на конце. | 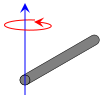 | |
| Тонкий стержень вдоль оси Y длиной l и массой m относительно центра. |  | |
| Сплошной цилиндр радиуса r , высоты h и массы m. | 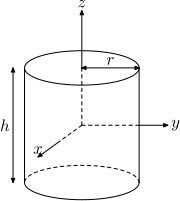 | |
| Толстостенная цилиндрическая трубка с открытыми концами внутреннего радиуса r 1 , наружного радиуса r 2 , длины h и массы m. | 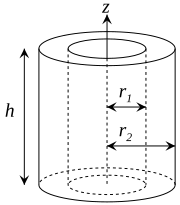 |
См. также [ править ]
Примечания [ править ]
- ^ Ширина перпендикулярно оси вращения (сторона пластины); высота (параллельно оси) не имеет значения.
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б с д и ж г час я Раймонд А. Сервей (1986). Физика для ученых и инженеров (2-е изд.). Издательство Колледжа Сондерса. п. 202 . ISBN 0-03-004534-7 .
- ^ Классическая механика — Момент инерции однородного полого цилиндра. Архивировано 7 февраля 2008 г. в Wayback Machine . LivePhysics.com. Проверено 31 января 2008 г.
- ^ Jump up to: Перейти обратно: а б с д и Саттерли, Джон (1958). «Моменты инерции некоторых многогранников». Математический вестник . 42 (339). Математическая ассоциация: 11–13. дои : 10.2307/3608345 . JSTOR 3608345 . S2CID 125538455 .
- ^ Jump up to: Перейти обратно: а б с д Фердинанд П. Бир и Э. Рассел Джонстон-младший (1984). Векторная механика для инженеров, четвертое изд . МакГроу-Хилл. п. 911. ИСБН 0-07-004389-2 .
- ^ Jump up to: Перейти обратно: а б Эрик В. Вайсштейн . «Момент инерции — Кольцо» . Вольфрам Исследования . Проверено 14 декабря 2016 г.
- ^ Джереми Татум. «2.20: Эллипсы и эллипсоиды» . phys.libretexts.org . Проверено 1 мая 2023 г.
- ^ см., например «Формула расчета момента инерции J» . www.mikipulley.co.jp . Проверено 30 апреля 2023 г.
- ^ А. Панагопулос и Г. Халкиадакис. Момент инерции потенциально наклоненных кубоидов. Технический отчет, Университет Саутгемптона, 2015 г.
- ^ Jump up to: Перейти обратно: а б Дэвид Морин (2010). Введение в классическую механику: с проблемами и решениями; первое издание (8 января 2010 г.) . Издательство Кембриджского университета. п. 320 . ISBN 978-0521876223 .








































































