Список вторых моментов площади
Ниже приводится список вторых моментов площади некоторых фигур. Второй момент площади , также известный как момент инерции площади, представляет собой геометрическое свойство площади, которое отражает, как ее точки распределены относительно произвольной оси. Единицей измерения второго момента площади является длина в четвертой степени, L. 4 , и не следует путать с моментом инерции массы . Однако если деталь тонкая, момент инерции массы равен плотности площади , умноженной на момент инерции площади.
Вторые моменты площади
[ редактировать ]Обратите внимание, что для второго момента уравнений площади в таблице ниже: и
| Описание | Фигура | Второй момент площади | Комментарий |
|---|---|---|---|
| Заполненная круглая область радиуса r |  | [1] | — второй полярный момент площади . |
| Кольцевое пространство внутреннего радиуса r 1 и внешнего радиуса r 2 |  | Для тонких трубок и и так для первого заказа в , . Итак, для тонкой трубки и . | |
| Заполненный круговой сектор с углом θ в радианах и радиусом r относительно оси, проходящей через центр тяжести сектора и центр круга. |  | Эта формула справедлива только для 0 ≤ ≤ | |
| Заполненный полукруг радиусом r относительно горизонтальной линии, проходящей через центр тяжести области. |  | [2] | |
| Заполненный полукруг, как указано выше, но относительно оси, коллинеарной основанию. | 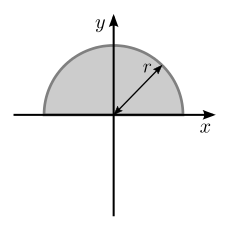 | [2] | : Это следствие теоремы о параллельности осей и того факта, что расстояние между осями X предыдущего и этого составляет |
| Заполненная четверть круга радиуса r с осями, проходящими через основания. |  | [3] | |
| Заполненная четверть круга радиуса r с осями, проходящими через центр тяжести. |  | [3] | Это следствие теоремы о параллельных осях и того факта, что расстояние между этими двумя осями равно |
| Заполненный эллипс , радиус которого по оси x равен a , а радиус по оси y равен b. |  | ||
| Заполненная прямоугольная область с базовой шириной b и высотой h. | 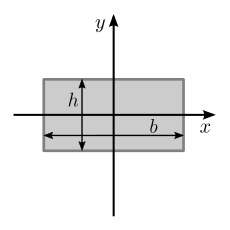 | [4] | |
| Заполненная прямоугольная область, как указано выше, но относительно оси, коллинеарной основанию. |  | [4] | Это результат теоремы о параллельной оси. |
| Полый прямоугольник с внутренним прямоугольником, ширина которого равна b 1 , а высота h 1. |  | ||
| Заполненная треугольная область с шириной основания b , высотой h и смещением верхней вершины a относительно оси, проходящей через центроид. |  | [5] | |
| Заполненная треугольная область, как указано выше, но относительно оси, коллинеарной основанию. |  | [5] | Это следствие теоремы о параллельной оси. |
| Равносторонний угол, обычно встречающийся в инженерных приложениях. |  | это часто неиспользуемый «второй момент площади произведения», используемый для определения главных осей. |
| Правильные многоугольники | |||
|---|---|---|---|
| Описание | Фигура | Второй момент площади | Комментарий |
| Заполненный правильный (равнобуквенный) треугольник со стороной a. |  | [6] | Результат действителен как для горизонтальной, так и для вертикальной оси, проходящей через центр тяжести, и, следовательно, также действителен для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников . |
| Заполненный квадрат со стороной a |  | [6] | Результат действителен как для горизонтальной, так и для вертикальной оси, проходящей через центр тяжести, и, следовательно, также действителен для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников . |
| Заполненный правильный шестиугольник со стороной a. |  | [6] | Результат действителен как для горизонтальной, так и для вертикальной оси, проходящей через центр тяжести, и, следовательно, также действителен для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников . |
| Заполненный правильный восьмиугольник со стороной длиной a. |  | [6] | Результат действителен как для горизонтальной, так и для вертикальной оси, проходящей через центр тяжести, и, следовательно, также действителен для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников . |
Теорема о параллельной оси
[ редактировать ]
Теорему о параллельной оси можно использовать для определения второго момента площади твердого тела относительно любой оси, учитывая второй момент площади тела относительно параллельной оси, проходящей через центр тяжести тела, площадь поперечного сечения и расстояние по перпендикуляру ( г ) между осями.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ "Круг" . еФунда . Проверено 30 декабря 2006 г.
- ^ Jump up to: а б «Круглая половина» . еФунда . Проверено 30 декабря 2006 г.
- ^ Jump up to: а б «Четверть круга» . еФунда . Проверено 30 декабря 2006 г.
- ^ Jump up to: а б «Прямоугольная площадь» . еФунда . Проверено 30 декабря 2006 г.
- ^ Jump up to: а б «Треугольная площадка» . еФунда . Проверено 30 декабря 2006 г.
- ^ Jump up to: а б с д Янг, Уоррен С; Будинас, Ричард Г. «Приложение A: Свойства плоской площади». Формулы Рорка для стресса и напряжения. Седьмое издание (PDF) . стр. 802–812 . Проверено 23 декабря 2022 г.
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )


![{\displaystyle {\begin{aligned}I_{x}&={\frac {\pi }{4}}r^{4}\\[3pt]I_{y}&={\frac {\pi } 4}}r^{4}\\[3pt]I_{z}&={\frac {\pi }{2}}r^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/278e00f090677da6ac3cd226e78a98bf21e3e8ad)

![{\displaystyle {\begin{aligned}I_{x}&={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4} \right)\\[3pt]I_{y}&={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\ right)\\[3pt]I_{z}&={\frac {\pi }{2}}\left({r_{2}}^{4}-{r_{1}}^{4}\right )\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2c0dc505866915f275ecd4962638f82248bf853)









![{\displaystyle {\begin{aligned}I_{x}&=\left({\frac {\pi }{8}}-{\frac {8}{9\pi }}\right)r^{4} \approx 0,1098r^{4}\\[3pt]I_{y}&={\frac {\pi r^{4}}{8}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddc0a8acc04324651c3bc2579b1cb8452e1ef66d)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {\pi r^{4}}{8}}\\[3pt]I_{y}&={\frac {\pi r^ {4}}{8}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/277b9ec1de780c3a576a1007c4d2458360987062)


![{\displaystyle {\begin{aligned}I_{x}&={\frac {\pi r^{4}}{16}}\\[3pt]I_{y}&={\frac {\pi r^ {4}}{16}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/764c8723a3141ac5d7ad49ca7abd6d69ef13984b)
![{\displaystyle {\begin{aligned}I_{x}&=\left({\frac {\pi }{16}}-{\frac {4}{9\pi }}\right)r^{4} \approx 0,0549r^{4}\\[3pt]I_{y}&=\left({\frac {\pi }{16}}-{\frac {4}{9\pi }}\right)r ^{4}\приблизительно 0,0549r^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa80a92550ec7bef1d6b8d5acc4ed7a04ec84bfa)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {\pi }{4}}ab^{3}\\[3pt]I_{y}&={\frac {\pi } 4}}a^{3}b\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e07bb49e05192b23a5e658bfb015da92b15cb4b)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {bh^{3}}{12}}\\[3pt]I_{y}&={\frac {b^{3}h }{12}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21d0bddcf815ee4746396673832c2d9458d131f5)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {bh^{3}}{3}}\\[3pt]I_{y}&={\frac {b^{3}h }{3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9900f74a013e4b660eebfcf99ea54f3e2a42320a)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {bh^{3}-b_{1}{h_{1}}^{3}}{12}}\\[3pt]I_ {y}&={\frac {b^{3}h-{b_{1}}^{3}h_{1}}{12}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e3784d81914f238868aec3ea913cc280a599e7c)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {bh^{3}}{36}}\\[3pt]I_{y}&={\frac {b^{3}hb ^{2}ha+bha^{2}}{36}}\\[3pt]I_{xy}&=-{\frac {bh^{2}}{72}}(b-2a)\end{ выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/779393bd3a378cb18b44f551ad3e88c325584e00)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {bh^{3}}{12}}\\[3pt]I_{y}&={\frac {b^{3}h +b^{2}ха+бха^{2}}{12}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bc71985a387580b8666b40ce5cdcb6ad7869cd0)
![{\displaystyle {\begin{aligned}I_{x}=I_{y}&={\frac {t(5L^{2}-5Lt+t^{2})(L^{2}-Lt+t ^{2})}{12(2L-t)}}\\[3pt]I_{(xy)}&={\frac {L^{2}t(Lt)^{2}}{4(t -2L)}}\\[3pt]I_{a}&={\frac {t(2L-t)(2L^{2}-2Lt+t^{2})}{12}}\\[3pt ]I_{b}&={\frac {t(2L^{4}-4L^{3}t+8L^{2}t^{2}-6Lt^{3}+t^{4})} {12(2L-t)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a62f26c9790cae3a20588fa574b3d34f268216ec)

![{\displaystyle {\begin{aligned}I_{x}&={\frac {a^{4}}{32{\sqrt {3}}}}\approx 0,01804a^{4}\\[3pt]I_ {y}&={\frac {a^{4}}{32{\sqrt {3}}}}\approx 0,01804a^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04f1cdf57241346ae708bb33fa7f172beea6b06e)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {a^{4}}{12}}\\[3pt]I_{y}&={\frac {a^{4}} {12}}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b6c0c9bede7b5176e57a93204ce52d9bcdea033)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {5{\sqrt {3}}}{16}}a^{4}\approx 0,54126a^{4}\\[3pt] I_{y}&={\frac {5{\sqrt {3}}}{16}}a^{4}\approx 0.54126a^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/accebf245f55a7b16ced477e55c60c7059d407cb)
![{\displaystyle {\begin{aligned}I_{x}&={\frac {11+8{\sqrt {2}}}{12}}a^{4}\approx 1,85947a^{4}\\[ 3pt]I_{y}&={\frac {11+8{\sqrt {2}}}{12}}a^{4}\approx 1.85947a^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1de48b68d2c6b13a938881757f6df6daa2dbbd3d)
