Второй полярный момент площади

Второй полярный момент площади , также известный (неверно, в просторечии) как «полярный момент инерции» или даже «момент инерции», представляет собой величину, используемую для описания сопротивления крутильной деформации ( прогибу ) в объектах (или сегментах объекта). объект) с неизменным поперечным сечением и без значительного коробления или деформации вне плоскости. ^[1] Это составляющая второго момента площади , связанного теоремой о перпендикулярной оси . Если плоский второй момент площади описывает сопротивление объекта отклонению ( изгибу ), когда он подвергается воздействию силы, приложенной к плоскости, параллельной центральной оси, то полярный второй момент площади описывает сопротивление объекта отклонению, когда он подвергается воздействию момента, приложенного в плоскость, перпендикулярная центральной оси объекта (т.е. параллельная поперечному сечению). Аналогично планарному второму моменту расчета площади ( $I_{x}$ , $I_{y}$ , и $I_{xy}$ ), полярный второй момент площади часто обозначается как $I_{z}$ . Хотя в некоторых учебниках по инженерному делу и академических публикациях это также обозначается как $J$ или $J_{z}$ этому обозначению следует уделить пристальное внимание, чтобы его не спутать с постоянной кручения , $J_{t}$ , используется для нецилиндрических объектов.

Проще говоря, полярный момент площади — это сопротивление вала или балки искажению при кручении в зависимости от его формы. Жесткость зависит только от площади поперечного сечения объекта и не зависит от состава его материала или модуля сдвига . Чем больше величина второго полярного момента площади, тем больше крутильная жесткость объекта.

Определение

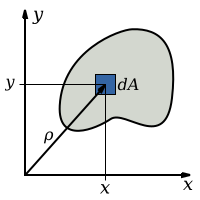
Уравнение, описывающее полярный момент площади, представляет собой кратный интеграл по площади поперечного сечения: $A$ , объекта.

$J=\iint _{A}r^{2}\,dA$ где $r$ расстояние до элемента $dA$ .

Подставляя $x$ и $y$ компоненты, используя теорему Пифагора : $J=\iint _{A}\left(x^{2}+y^{2}\right)dx\,dy$ $J=\iint _{A}x^{2}\,dx\,dy+\iint _{A}y^{2}\,dx\,dy$

Учитывая плоские вторые моменты уравнений площади, где: $I_{x}=\iint _{A}y^{2}dx\,dy$ $I_{y}=\iint _{A}x^{2}dx\,dy$

Показано, что полярный момент площади можно описать как сумму $x$ и $y$ плоские моменты площади, $I_{x}$ и $I_{y}$ $\therefore J=I_{z}=I_{x}+I_{y}$

Это также показано в теореме о перпендикулярной оси . ^[2] Для объектов, обладающих вращательной симметрией, ^[3] например, цилиндр или полая трубка, уравнение можно упростить до: $J=2I_{x}$ или $J=2I_{y}$

Для круглого сечения радиусом $R$ : $I_{z}=\int _{0}^{2\pi }\int _{0}^{R}r^{2}(r\,dr\,d\phi )={\frac {\pi R^{4}}{2}}$

Единица

Единицей СИ для полярного второго момента площади , как и планарного второго момента площади , являются метры в четвертой степени ( м ⁴), и дюймы в четвертой степени ( в ⁴) в обычных и имперских единицах США .

Ограничения

Полярного второго момента площади может быть недостаточно для использования для анализа балок и валов с некруглым поперечным сечением из-за их склонности к короблению при скручивании, вызывая деформации вне плоскости. В таких случаях следует заменить константу кручения , в которую включена соответствующая константа деформации, чтобы компенсировать эффект деформации. В рамках этого есть статьи, которые различают полярный второй момент площади , $I_{z}$ , и постоянная кручения , $J_{t}$ , больше не пользуюсь $J$ для описания полярного второго момента площади. ^[4]

Для объектов со значительным изменением поперечного сечения (вдоль оси приложенного крутящего момента), которые невозможно анализировать по сегментам, возможно, придется использовать более сложный подход. См. 3-D эластичность .

Приложение

Хотя полярный второй момент площади чаще всего используется для расчета углового смещения объекта, подвергающегося действию момента ( крутящего момента ), приложенного параллельно поперечному сечению, указанное значение жесткости не имеет никакого отношения к сопротивлению скручиванию, обеспечиваемому Объект как функция составляющих его материалов. Жесткость, обеспечиваемая материалом объекта, является характеристикой его модуля сдвига . $G$ . Сочетая эти две особенности с длиной вала, $L$ , можно рассчитать угловое отклонение вала, $\theta$ , из-за приложенного крутящего момента, $T$ : $\theta ={\frac {TL}{JG}}$

Как показано, чем больше модуль сдвига материала и полярный второй момент площади (т.е. больше площадь поперечного сечения), тем выше сопротивление крутильному отклонению.

Полярный второй момент площади появляется в формулах, описывающих напряжение кручения и угловое смещение.

Крутильные напряжения: $\tau ={\frac {T\,r}{J_{z}}}$ где $\tau$ - напряжение скручивания, $T$ - приложенный крутящий момент, $r$ расстояние от центральной оси, а $J_{z}$ – полярный второй момент площади.

Примечание. В круглом валу напряжение сдвига максимально на поверхности вала.

Пример расчета

Расчет радиуса вала паровой турбины турбоагрегата:

Предположения:

Мощность, передаваемая по валу, составляет 1000 МВт ; это типично для крупной атомной электростанции.
Предел текучести стали, из которой изготовлен вал ( τ _{текучесть} ): 250 × 10 ⁶ Н/м ².
Электричество имеет частоту 50 Гц ; это типичная частота в Европе. В Северной Америке частота составляет 60 Гц. Это предполагает, что существует корреляция 1:1 между скоростью вращения турбины и частотой сети.

Угловую частоту можно рассчитать по следующей формуле: $\omega =2\pi f$

Крутящий момент, передаваемый валом, связан с мощностью следующим уравнением: $P=T\omega$

Таким образом, угловая частота равна 314,16 рад / с , а крутящий момент 3,1831 × 10. ⁶ Н·м .

Максимальный крутящий момент: $T_{\max }={\frac {\tau _{\max }J_{z}}{r}}$

После замены полярного второго момента площади получается следующее выражение: $r={\sqrt[{3}]{\frac {2T_{\max }}{\pi \tau _{\max }}}}$

Радиус диаметр r м = =0,200 200 мм, или 400 мм . Если добавить коэффициент запаса 5 и пересчитать радиус с допустимым напряжением, равным τ _adm = τ, _{получим} /5, то в результате получится радиус 0,343 м или диаметр 690 мм, приблизительный размер Вал турбореактивной установки на атомной электростанции.

Сравнение полярных вторых моментов площади и моментов инерции (вторых моментов массы)

Полый цилиндр

Полярный второй момент площади: $I_{z}={\frac {\pi \left(D^{4}-d^{4}\right)}{32}}$

Момент инерции: $I_{c}=I_{z}\rho l={\frac {\pi \rho l\left(D^{4}-d^{4}\right)}{64}}$

Твердый цилиндр

Полярный второй момент площади $I_{z}={\frac {\pi D^{4}}{32}}$

Момент инерции $I_{c}=I_{z}\rho l={\frac {\pi \rho lD^{4}}{64}}$ где:

$d$ внутренний диаметр в метрах (м)
$D$ внешний диаметр в метрах (м)
$I_{c}$ момент инерции в кг·м ²
$I_{z}$ - полярный второй момент площади в метрах в четвертой степени (м ⁴)
$l$ длина цилиндра в метрах (м)
$\rho$ - удельная масса в кг/м ³

См. также

Ссылки

^ Угурал AC, Фенстер СК. Повышенная прочность и прикладная эластичность. 3-е изд. Prentice-Hall Inc. Энглвуд Клиффс, Нью-Джерси. 1995. ISBN 0-13-137589-X .
^ «Момент инерции; Определение с примерами» . www.efunda.com .
^ Обрегон, Хоакин (2012). Механическая симметрия . Авторский дом. ISBN 978-1-4772-3372-6 .
^ галтор. «В чем разница между полярным вторым моментом площади («Полярный момент инерции»), IPIP, и постоянной крутильного движения JTJT поперечного сечения?» .

Внешние ссылки

Кручение валов - Engineeringtoolbox.com
Упругие свойства и модуль Юнга некоторых материалов
База данных свойств материалов — matweb.com

[ugural-1] Угурал AC, Фенстер СК. Повышенная прочность и прикладная эластичность. 3-е изд. Prentice-Hall Inc. Энглвуд Клиффс, Нью-Джерси. 1995. ISBN 0-13-137589-X .

[2] «Момент инерции; Определение с примерами» . www.efunda.com .

[3] Обрегон, Хоакин (2012). Механическая симметрия . Авторский дом. ISBN 978-1-4772-3372-6 .

[4] галтор. «В чем разница между полярным вторым моментом площади («Полярный момент инерции»), IPIP, и постоянной крутильного движения JTJT поперечного сечения?» .

[1]

[2]

[3]

[4]