Прогиб (инженерия)

В технике строительной прогиб — это степень, в которой часть длинного элемента конструкции (например, балки ) деформируется вбок (в направлении, поперечном его продольной оси) под нагрузкой . Его можно выразить количественно в терминах угла ( угловое смещение ) или расстояния (линейное смещение ).Продольная деформация (в направлении оси) называется удлинением .

Расстояние отклонения элемента под нагрузкой можно рассчитать путем интегрирования функции, которая математически описывает наклон изогнутой формы элемента под этой нагрузкой. Существуют стандартные формулы для отклонения балок обычных конфигураций и случаев нагрузки в отдельных местах. такие методы, как виртуальная работа , прямое интегрирование , метод Кастильяно , метод Маколея или метод прямой жесткости В противном случае используются . Прогиб балочных элементов обычно рассчитывается на основе уравнения балки Эйлера – Бернулли, а прогиб пластинчатого или оболочечного элемента рассчитывается с использованием теории пластины или оболочки .

Примером использования прогиба в этом контексте является строительство зданий. Архитекторы и инженеры выбирают материалы для различных применений.

Прогиб балки под различные нагрузки и опоры

Балки могут сильно различаться по своей геометрии и составу. Например, балка может быть прямой или изогнутой. Он может иметь постоянное поперечное сечение или сужаться. Он может быть полностью изготовлен из одного и того же материала (гомогенный) или состоять из разных материалов (композитный). Некоторые из этих вещей затрудняют анализ, но многие инженерные приложения включают в себя не такие сложные случаи. Анализ упрощается, если:

Балка изначально прямая, любое сужение незначительно.
Балка испытывает только линейную упругую деформацию.
Балка тонкая (отношение ее длины к высоте больше 10)
Учитываются только небольшие прогибы (максимальный прогиб менее 1/10 пролета ) .

В этом случае уравнение, определяющее прогиб балки ( $w$ ) можно аппроксимировать как: ${\frac {\mathrm {d} ^{2}w(x)}{\mathrm {d} x^{2}}}={\frac {M(x)}{E(x)I(x)}}$ где вторая производная его отклоненной формы относительно $x$ ( $x$ горизонтальное положение по длине балки) интерпретируется как ее кривизна, $E$ – модуль Юнга , $I$ - момент инерции площади поперечного сечения, а $M$ – внутренний изгибающий момент балки.

Если, кроме того, балка неконическая, однородная и на нее действует распределенная нагрузка $q$ , приведенное выше выражение можно записать как : $EI~{\frac {\mathrm {d} ^{4}w(x)}{\mathrm {d} x^{4}}}=q(x)$

Это уравнение можно решить для различных нагрузок и граничных условий. Ниже приведен ряд простых примеров. Выраженные формулы представляют собой приближения, разработанные для длинных, тонких, однородных призматических балок с небольшими отклонениями и линейными упругими свойствами. При этих ограничениях аппроксимации должны давать результаты в пределах 5% от фактического отклонения.

Консольные балки

Консольные балки имеют один конец фиксированным, поэтому наклон и прогиб на этом конце должны быть равны нулю.

Схема прогиба консольной балки.

Консольные балки с торцевой нагрузкой

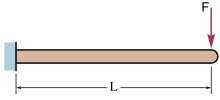
Упругий прогиб $\delta$ и угол отклонения $\phi$ (в радианах ) на свободном конце на изображении в качестве примера: Консольную балку (невесомую) с концевой нагрузкой можно рассчитать (на свободном конце B) с помощью: ^[1] ${\begin{aligned}\delta _{B}&={\frac {FL^{3}}{3EI}}\\[1ex]\phi _{B}&={\frac {FL^{2}}{2EI}}\end{aligned}}$ где

$F$ = сила, действующая на кончик балки
$L$ = длина балки (пролет)
$E$ = модуль упругости
$I$ = момент инерции площади поперечного сечения балки

Обратите внимание, что если пролет увеличивается вдвое, прогиб увеличивается в восемь раз. Отклонение в любой точке, $x$ , вдоль пролета консольной балки, нагруженной на конце, можно рассчитать с помощью: ^[1] ${\begin{aligned}\delta _{x}&={\frac {Fx^{2}}{6EI}}(3L-x)\\[1ex]\phi _{x}&={\frac {Fx}{2EI}}(2L-x)\end{aligned}}$

Примечание: В $x=L$ (конец балки), $\delta _{x}$ и $\phi _{x}$ уравнения идентичны $\delta _{B}$ и $\phi _{B}$ уравнения выше.

Консольные балки с равномерной нагрузкой

Прогиб свободного конца B консольной балки под действием равномерной нагрузки определяется по формуле: ^[1] ${\begin{aligned}\delta _{B}&={\frac {qL^{4}}{8EI}}\\[1ex]\phi _{B}&={\frac {qL^{3}}{6EI}}\end{aligned}}$ где

$q$ = равномерная нагрузка на балку (сила на единицу длины)
$L$ = длина балки
$E$ = модуль упругости
$I$ = момент инерции площади поперечного сечения

Отклонение в любой точке, $x$ , вдоль пролета равномерно нагруженной консольной балки можно рассчитать по формуле: ^[1] ${\begin{aligned}\delta _{x}&={\frac {qx^{2}}{24EI}}\left(6L^{2}-4Lx+x^{2}\right)\\[1ex]\phi _{x}&={\frac {qx}{6EI}}\left(3L^{2}-3Lx+x^{2}\right)\end{aligned}}$

Просто опертые балки

Просто опертые балки имеют под концами опоры, допускающие вращение, но не прогибание.

Схема прогиба свободно опертой балки.

Простые балки с центральной нагрузкой

Отклонение в любой точке, $x$ , вдоль пролета свободно опертой балки с центральной нагрузкой можно рассчитать по формуле: ^[1] $\delta _{x}={\frac {Fx}{48EI}}\left(3L^{2}-4x^{2}\right)$ для $0\leq x\leq {\frac {L}{2}}$

Особый случай упругого прогиба в средней точке C балки, нагруженной в ее центре и поддерживаемой двумя простыми опорами, определяется следующим образом: ^[1] $\delta _{C}={\frac {FL^{3}}{48EI}}$ где

$F$ = сила, действующая на центр балки
$L$ = длина балки между опорами
$E$ = модуль упругости
$I$ = момент инерции площади поперечного сечения

Простые балки со смещенной от центра нагрузкой

Максимальный упругий прогиб балки, опирающейся на две простые опоры, нагруженные на расстоянии $a$ от ближайшей поддержки, предоставляется: ^[1] $\delta _{\text{max}}={\frac {Fa\left(L^{2}-a^{2}\right)^{3/2}}{9{\sqrt {3}}LEI}}$ где

$F$ = сила, действующая на балку
$L$ = длина балки между опорами
$E$ = модуль упругости
$I$ = момент инерции площади поперечного сечения
$a$ = расстояние от груза до ближайшей опоры

Максимальное отклонение происходит на расстоянии $x_{1}$ от ближайшей поддержки и предоставляется: ^[1] $x_{1}={\sqrt {\frac {L^{2}-a^{2}}{3}}}$

Равномерно нагруженные простые балки

Упругий прогиб (в средней точке C) балки, поддерживаемой двумя простыми опорами, под действием равномерной нагрузки (как показано на рисунке) определяется по формуле: ^[1] $\delta _{C}={\frac {5qL^{4}}{384EI}}$ где

$q$ = равномерная нагрузка на балку (сила на единицу длины)
$L$ = длина балки
$E$ = модуль упругости
$I$ = момент инерции площади поперечного сечения

Отклонение в любой точке, $x$ , вдоль пролета равномерно нагруженной свободно опертой балки можно рассчитать по формуле: ^[1] $\delta _{x}={\frac {qx}{24EI}}\left(L^{3}-2Lx^{2}+x^{3}\right)$

Комбинированные нагрузки

Прогиб балок при сочетании простых нагрузок можно рассчитать по принципу суперпозиции .

Изменение длины

Изменение длины $\Delta L$ балки в конструкциях обычно незначительна, но ее можно рассчитать путем интегрирования уклона $\theta _{x}$ функция, если функция отклонения $\delta _{x}$ известен всем $x$ .

Где:

$\Delta L$ = изменение длины (всегда отрицательное)
$\theta _{x}$ = функция наклона (первая производная $\delta _{x}$ )
$\Delta L=-{\frac {1}{2}}\int _{0}^{L}(\theta (x))^{2}dx$ ^[2]

Если балка однородна и известен прогиб в любой точке, его можно рассчитать, не зная других свойств балки.

Единицы

Приведенные выше формулы требуют использования согласованного набора единиц. Большинство расчетов будет производиться в Международной системе единиц (СИ) или обычных единицах измерения США, хотя существует множество других систем единиц.

Международная система (СИ)

Сила: Ньютоны ( $\mathrm {N}$ )
Длина: метры ( $\mathrm {m}$ )
Модуль упругости: $\mathrm {\frac {N}{m^{2}}} =\mathrm {Pa}$
Момент инерции: $\mathrm {m^{4}}$

Обычные единицы США (США)

Сила: фунты силы ( $\mathrm {lbf}$ )
Длина: дюймы ( $\mathrm {in}$ )
Модуль упругости: $\mathrm {\frac {lbf}{in^{2}}}$
Момент инерции: $\mathrm {in^{4}}$

Другие

Могут использоваться и другие единицы, если они непротиворечивы. Например, иногда килограмм-сила ( $\mathrm {kgf}$ ) единица измерения нагрузок. В таком случае модуль упругости необходимо преобразовать в $\mathrm {\frac {kgf}{m^{2}}}$ .

Структурный прогиб

Строительные нормы и правила определяют максимальный прогиб, обычно как долю пролета, например 1/400 или 1/600. Минимальные требуемые размеры элемента могут определяться либо предельным состоянием прочности (допустимое напряжение), либо предельным состоянием эксплуатационной пригодности (среди прочего, соображениями прогиба).

Прогиб необходимо учитывать с точки зрения конструкции. При проектировании стальной рамы для удержания застекленной панели допускается лишь минимальное отклонение, чтобы предотвратить разрушение стекла.

Отклоненную форму балки можно представить интегрированной диаграммой моментов (дважды повернутой и перенесенной для обеспечения условий опоры).

См. также

Метод отклонения уклона

Ссылки

^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Гир, Джеймс М.; Гудно, Барри Дж. (январь 2012 г.). Механика материалов (Восьмое изд.). стр. 1083–1087. ISBN 978-1-111-57773-5 .
^ Формулы Рорка для стресса и деформации, 8-е издание, уравнения 8.1-14.

Внешние ссылки

[gere-1] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Гир, Джеймс М.; Гудно, Барри Дж. (январь 2012 г.). Механика материалов (Восьмое изд.). стр. 1083–1087. ISBN 978-1-111-57773-5 .

[2] Формулы Рорка для стресса и деформации, 8-е издание, уравнения 8.1-14.

[1]

[2]