Метод Кастильяно

Метод Кастильяно названный в честь Карло Альберто Кастильяно , — это метод определения перемещений линейно-упругой системы на основе частных производных энергии , . Он известен своими двумя теоремами. Основную концепцию можно легко понять, если вспомнить, что изменение энергии равно вызвавшей силе, умноженной на результирующее смещение. Следовательно, вызывающая сила равна изменению энергии, разделенному на результирующее смещение. Альтернативно, результирующее смещение равно изменению энергии, разделенному на вызывающую силу. Частные производные необходимы, чтобы связать вызывающие силы и результирующие смещения с изменением энергии.

Первая теорема Кастильяно - для сил в упругой конструкции

Метод Кастильяно для расчета сил представляет собой применение его первой теоремы, которая гласит:

Если энергию деформации упругой конструкции можно выразить как функцию обобщенного смещения q _i, то частная производная энергии деформации по обобщенному смещению дает обобщенную силу Q _i .

В форме уравнения $Q_{i}={\frac {\partial U}{\partial q_{i}}}$ где $U$ – энергия деформации.
Если кривая сила-перемещение нелинейна, то вместо энергии деформации необходимо использовать дополнительную энергию деформации. ^{[ 1 ]}
Вторая теорема Кастильяно – для перемещений в линейно упругой конструкции.

Метод Кастильяно для расчета перемещений представляет собой применение его второй теоремы, которая гласит:

Если энергию деформации линейно упругой конструкции можно выразить как функцию обобщенной силы Q _i, то частная производная энергии деформации по обобщенной силе дает обобщенное смещение q _i в направлении Q _i .

Как указано выше, это также может быть выражено как:
$q_{i}={\frac {\partial U}{\partial Q_{i}}}.$

Примеры

Для тонкой прямой консольной балки с нагрузкой P на конце смещение $\delta$ в конце можно найти по второй теореме Кастильяно:

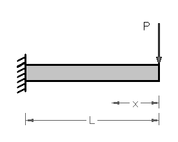
$\delta ={\frac {\partial U}{\partial P}}$ $\delta ={\frac {\partial }{\partial P}}\int _{0}^{L}{{\frac {M^{2}(x)}{2EI}}dx}={\frac {\partial }{\partial P}}\int _{0}^{L}{{\frac {(Px)^{2}}{2EI}}dx}$ где $E$ – модуль Юнга , $I$ - второй момент площади поперечного сечения, а $M(x)=Px$ является выражением внутреннего момента в точке на расстоянии $x$ с конца. Интеграл оценивается как: ${\begin{aligned}\delta &=\int _{0}^{L}{{\frac {Px^{2}}{EI}}dx}\\&={\frac {PL^{3}}{3EI}}.\end{aligned}}$

В результате получается стандартная формула для консольных балок, испытывающих концевые нагрузки.

Теоремы Кастильяно применимы, если энергия деформации конечна. Это верно, если $m-i>n/2$ . ^{[ 2 ]} Это $m=1,2$ порядок энергии (= высшая производная по энергии), $i=0,1,2,3$ , — индекс дельты Дирака (одинарная сила, $i=0$ ) и $n=1,2,3$ это размерность пространства. Для уравнений второго порядка $m=1$ , принадлежат двум дельтам Дирака, $i=0$ , сила и $i=1$ , дислокации и уравнениям четвертого порядка, $m=2$ , четыре дельты Дирака, $i=0$ сила, $i=1$ момент, $i=2$ сгибать, $i=3$ дислокация.

Пример: Если тарелка, $m=1,n=2$ , нагружен одной силой, $i=0$ , неравенство неверно, $1-0\ngtr 2/2$ , тоже не в $3-D$ , $m=1,n=3,1-0\ngtr 3/2$ . Это не применимо и к мембране (Лаплас). $m=1,n=2,i=0$ или пластинка Рейсснера-Миндлина, $m=1,n=2,i=0$ . В общем случае теоремы Кастильяно неприменимы к $2-D$ и $3-D$ проблемы. Исключение составляет пластинка Кирхгофа. $m=2,n=2,i=0$ , с $2-0>2/2$ . Но мгновение, $i=1$ , вызывает переполнение энергии пластины Кирхгофа, $2-1\ngtr 2/2$ . В $1-D$ задачи энергия деформации конечна, если $m-i>1/2$ .

На теорему Менабреа распространяется то же ограничение. Это нужно $m-i>n/$ 2 действителен. Это $i$ порядок реакции опоры, одиночная сила $i=0$ , момент $i=1$ . За исключением пластины Кирхгофа и $i=0$ (одиночная сила как опорная реакция), как правило, она недействительна в $2-D$ и $3-D$ потому что наличие точечных опор приводит к бесконечно большой энергии.

Внешние ссылки

Карло Альберто Кастильяно
Метод Кастильяно: некоторые примеры (на немецком языке)

Ссылки

^ История сопротивления материалов, Стивен П. Тимошенко, 1993, Dover Publications, Нью-Йорк.
^ Статика и функции влияния с современной точки зрения, Хартманн, Ян, глава 1.35. Теорема вложения Соболева, 2-е изд. 2021, Спрингер, с. 71

[1] История сопротивления материалов, Стивен П. Тимошенко, 1993, Dover Publications, Нью-Йорк.

[2] Статика и функции влияния с современной точки зрения, Хартманн, Ян, глава 1.35. Теорема вложения Соболева, 2-е изд. 2021, Спрингер, с. 71

[ 1 ]

[ 2 ]