Виртуальная работа

В механике виртуальная работа возникает при применении принципа наименьшего действия к изучению сил и движения механической системы . Работа , силы, действующей на частицу при ее движении вдоль перемещения различна для разных перемещений. Среди всех возможных смещений, за которыми может следовать частица, называемых виртуальными смещениями , одно действие будет минимизировано. Таким образом, это смещение представляет собой смещение, за которым следует частица в соответствии с принципом наименьшего действия.

Работа силы над частицей вдоль виртуального перемещения называется виртуальной работой.

Исторически виртуальная работа и связанное с ней вариационное исчисление были сформулированы для анализа систем твердых тел. ^[1] но они были разработаны и для изучения механики деформируемых тел. ^[2]

История [ править ]

Принцип виртуальной работы всегда использовался в той или иной форме, начиная с античности, при изучении статики. Его использовали греки, средневековые арабы и латиняне, а также итальянцы эпохи Возрождения как «закон рычага». ^[3] Идея виртуальной работы в разной степени общности использовалась многими известными физиками 17 века, такими как Галилей, Декарт, Торричелли, Уоллис и Гюйгенс, при решении задач статики. ^[3]Работая с концепциями Лейбница, Иоганн Бернулли систематизировал принцип виртуальной работы и подробно изложил концепцию бесконечно малого перемещения. Он мог решать задачи как для твердых тел, так и для жидкостей. Версия виртуального закона работы Бернулли появилась в его письме Пьеру Вариньону в 1715 году, которое позже было опубликовано во втором томе книги Вариньона «Новая механика или статистика» в 1725 году. Эта формулировка принципа сегодня известна как принцип виртуальных скоростей и обычно считается как прообраз современных принципов виртуальной работы. ^[3]В 1743 году Даламбер опубликовал свой «Трактат о динамике» , в котором применил принцип виртуальной работы, основанный на работах Бернулли, для решения различных задач динамики. Его идея заключалась в том, чтобы преобразовать динамическую задачу в статическую путем введения силы инерции . ^[4]В 1768 году Лагранж представил принцип виртуальной работы в более эффективной форме, введя обобщенные координаты, и представил его как альтернативный принцип механики, с помощью которого можно решить все проблемы равновесия. Систематическое изложение программы Лагранжа применения этого подхода ко всей механике, как статической, так и динамической, по сути, принципа Даламбера , было дано в его «Аналитической механике» 1788 года. ^[3] Хотя Лагранж представил свою версию принципа наименьшего действия еще до этой работы, он признал принцип виртуальной работы более фундаментальным, главным образом потому, что его можно было рассматривать как основу всей механики, в отличие от современного понимания, согласно которому наименьшее действие не учитывает неконсервативные силы. ^[3]

Обзор [ править ]

Если сила действует на частицу при ее движении из точки $A$ В точку $B$ , тогда для каждой возможной траектории, которую может пройти частица, можно вычислить полную работу, совершаемую силой на этом пути. Принцип виртуальной работы , представляющий собой форму принципа наименьшего действия, применяемого к этим системам, гласит, что путь, по которому фактически следует частица, — это тот путь, для которого разница между работой по этому пути и другими близкими путями равна нулю ( до первого заказа). Формальная процедура вычисления разности функций, оцениваемых на соседних путях, представляет собой обобщение производной, известной из дифференциального исчисления, и называется вариационным исчислением .

Рассмотрим точечную частицу, движущуюся по траектории, описываемой функцией $\mathbf {r} (t)$ из точки $A$ , где $\mathbf {r} (t=t_{0})$ , В точку $B$ , где $\mathbf {r} (t=t_{1})$ . Возможно, частица движется от $A$ к $B$ по близлежащей тропе, описанной $\mathbf {r} (t)+\delta \mathbf {r} (t)$ , где $\delta \mathbf {r} (t)$ называется вариацией $\mathbf {r} (t)$ . Вариант $\delta \mathbf {r} (t)$ удовлетворяет требованию $\delta \mathbf {r} (t_{0})=\delta \mathbf {r} (t_{1})=0$ . Скалярные компоненты вариации $\delta r_{1}(t)$ , $\delta r_{2}(t)$ и $\delta r_{3}(t)$ называются виртуальными перемещениями. Это можно обобщить на произвольную механическую систему, определяемую обобщенными координатами. $q_{i}$ , $i=1,2,...,n$ . В этом случае изменение траектории $q_{i}(t)$ определяется виртуальными перемещениями $\delta q_{i}$ , $i=1,2,...,n$ .

Виртуальная работа — это общая работа, совершаемая приложенными силами и силами инерции механической системы при ее движении через набор виртуальных перемещений. При рассмотрении сил, приложенных к телу, находящемуся в статическом равновесии, принцип наименьшего действия требует, чтобы виртуальная работа этих сил была равна нулю.

Математическая обработка [ править ]

Рассмотрим частицу P , которая движется из точки A в точку B по траектории r ( t сила F ( r ( t ), при этом к ней приложена )). Работа силы F определяется интегралом

W=\int _{\mathbf {r} (t_{0})=A}^{\mathbf {r} (t_{1})=B}\mathbf {F} \cdot d\mathbf {r} =\int _{t_{0}}^{t_{1}}\mathbf {F} \cdot {\frac {d\mathbf {r} }{dt}}~dt=\int _{t_{0}}^{t_{1}}\mathbf {F} \cdot \mathbf {v} ~dt,

где d r — дифференциальный элемент вдоль кривой, которая является траекторией P , а v — его скорость. Важно отметить, что величина работы W зависит от траектории r ( t ).

Теперь рассмотрим частицу P , которая снова движется из точки A в точку B , но на этот раз она движется по ближайшей траектории, отличающейся от r ( t ) вариацией $δ r (t) = ε h (t)$ , где ε — масштабирование константа, которую можно сделать сколь угодно маленькой, а h ( t ) — произвольная функция, удовлетворяющая условию $h (t 0) = h (t 1) = 0$ . Предположим, что сила $F (r (t) + ε h (t))$ такая же, как $F (r (t))$ . Работа, совершаемая силой, определяется интегралом

{\bar {W}}=\int _{\mathbf {r} (t_{0})=A}^{\mathbf {r} (t_{1})=B}\mathbf {F} \cdot d(\mathbf {r} +\epsilon \mathbf {h} )=\int _{t_{0}}^{t_{1}}\mathbf {F} \cdot {\frac {d(\mathbf {r} (t)+\epsilon \mathbf {h} (t))}{dt}}~dt=\int _{t_{0}}^{t_{1}}\mathbf {F} \cdot (\mathbf {v} +\epsilon {\dot {\mathbf {h} }})~dt.

Вариация работы δW, связанная с этим близлежащим путем, известная как виртуальная работа , может быть вычислена как

\delta W={\bar {W}}-W=\int _{t_{0}}^{t_{1}}(\mathbf {F} \cdot \epsilon {\dot {\mathbf {h} }})~dt.

нет никаких ограничений Если на движение P необходимы 3 параметра P , то для полного описания положения в любой момент времени t . Если имеется k ( k ≤ 3) ограничивающих сил, то n = (3 − k необходимо ) параметров. Следовательно, мы можем определить n обобщенных координат q _i ( t ) ( i = 1,..., n ) и выразить r ( t ) и $δ r = ε h (t)$ через обобщенные координаты. То есть,

\mathbf {r} (t)=\mathbf {r} (q_{1},q_{2},\dots ,q_{n};t),

\mathbf {h} (t)=\mathbf {h} (q_{1},q_{2},\dots ,q_{n};t).

Тогда производная вариации

δ r = ε h (t)

определяется выражением

{\frac {d}{dt}}\delta \mathbf {r} ={\frac {d}{dt}}\epsilon \mathbf {h} =\sum _{i=1}^{n}{\frac {\partial \mathbf {h} }{\partial q_{i}}}\epsilon {\dot {q}}_{i},

тогда у нас есть

\delta W=\int _{t_{0}}^{t_{1}}\left(\sum _{i=1}^{n}\mathbf {F} \cdot {\frac {\partial \mathbf {h} }{\partial q_{i}}}\epsilon {\dot {q}}_{i}\right)dt=\sum _{i=1}^{n}\left(\int _{t_{0}}^{t_{1}}\mathbf {F} \cdot {\frac {\partial \mathbf {h} }{\partial q_{i}}}\epsilon {\dot {q}}_{i}~dt\right).

Требование, чтобы виртуальная работа была равна нулю для произвольной вариации $(δr t) = εh, (t)$ эквивалентно набору требований

Q_{i}=\mathbf {F} \cdot {\frac {\partial \mathbf {h} }{\partial q_{i}}}=0,\quad i=1,\ldots ,n.

Члены Q _i называются обобщенными силами , связанными с виртуальным смещением δ r .

Статическое равновесие [ править ]

Статическое равновесие — это состояние, в котором чистая сила и чистый крутящий момент, действующие на систему, равны нулю. Другими словами, как линейный момент , так и угловой момент системы сохраняются. Принцип виртуальной работы гласит, что виртуальная работа приложенных сил равна нулю при всех виртуальных движениях системы из статического равновесия . Этот принцип можно обобщить так, что в него включены трехмерные вращения : виртуальная работа приложенных сил и приложенных моментов равна нулю для всех виртуальных движений системы из статического равновесия. То есть

\delta W=\sum _{i=1}^{m}\mathbf {F} _{i}\cdot \delta \mathbf {r} _{i}+\sum _{j=1}^{n}\mathbf {M} _{j}\cdot \delta \mathbf {\phi } _{j}=0,

где F _i , i = 1, 2, ..., m и M _j , j = 1, 2, ..., n — приложенные силы и приложенные моменты соответственно, а δ r _i , i = 1, 2 , ..., m и δ φ _j , j = 1, 2, ..., n — виртуальные перемещения и виртуальные вращения соответственно.

Предположим, что система состоит из N частиц и имеет f ( f ≤ 6 N ) степеней свободы . Достаточно использовать только f координаты, чтобы дать полное описание движения системы, поэтому f обобщенные координаты q _k , k = 1, 2, ..., f определяются так, что виртуальные движения могут быть выражены в терминах этих обобщенных координат . То есть,

\delta \mathbf {r} _{i}(q_{1},q_{2},\dots ,q_{f};t),\quad i=1,2,\dots ,m;

\delta \phi _{j}(q_{1},q_{2},\dots ,q_{f};t),\quad j=1,2,\dots ,n.

Затем виртуальную работу можно перепараметризовать с помощью обобщенных координат :

\delta W=\sum _{k=1}^{f}\left[\left(\sum _{i=1}^{m}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{k}}}+\sum _{j=1}^{n}\mathbf {M} _{j}\cdot {\frac {\partial \mathbf {\phi } _{j}}{\partial q_{k}}}\right)\delta q_{k}\right]=\sum _{k=1}^{f}Q_{k}\delta q_{k},

где обобщенные силы Q _k определяются как

Q_{k}=\sum _{i=1}^{m}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{k}}}+\sum _{j=1}^{n}\mathbf {M} _{j}\cdot {\frac {\partial \mathbf {\phi } _{j}}{\partial q_{k}}},\quad k=1,2,\dots ,f.

Кейн ^[5]показывает, что эти обобщенные силы также можно сформулировать через отношение производных по времени. То есть,

Q_{k}=\sum _{i=1}^{m}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {v} _{i}}{\partial {\dot {q}}_{k}}}+\sum _{j=1}^{n}\mathbf {M} _{j}\cdot {\frac {\partial \mathbf {\omega } _{j}}{\partial {\dot {q}}_{k}}},\quad k=1,2,\dots ,f.

Принцип виртуальной работы требует, чтобы виртуальная работа, совершаемая над системой силами F _i и моментами M _j, обращалась в нуль, если она находится в равновесии . Следовательно, обобщенные силы Q _k равны нулю, т.е.

\delta W=0\quad \Rightarrow \quad Q_{k}=0\quad k=1,2,\dots ,f.

Сдерживающие силы [ править ]

Важным преимуществом принципа виртуальной работы является то, что только силы, которые работают при движении системы через виртуальное перемещение для определения механики системы необходимы . В механической системе существует множество сил, которые при виртуальном перемещении не совершают работы , а значит, их не нужно учитывать в данном анализе. Двумя важными примерами являются (i) внутренние силы в твердом теле и (ii) силы ограничения в идеальном суставе .

Ланчош ^[1]представляет это как постулат: «Виртуальная работа сил реакции всегда равна нулю при любом виртуальном перемещении , которое находится в гармонии с заданными кинематическими ограничениями». Аргумент заключается в следующем. Принцип виртуальной работы гласит, что в состоянии равновесия виртуальная работа сил, приложенных к системе, равна нулю. Законы Ньютона гласят, что в состоянии равновесия приложенные силы равны и противоположны силам реакции или силам ограничения. Это означает, что виртуальная работа сил связи также должна быть равна нулю.

Закон рычага [ править ]

Рычаг моделируется как жесткий стержень , соединенный с опорной рамой шарнирным соединением, называемым точкой опоры. Рычаг приводится в действие путем приложения входной силы F _A в точке A , расположенной по координатному вектору r _A на стержне. Затем рычаг прикладывает выходную силу F _B в точке B, расположенной через r _B . Поворот рычага вокруг точки опоры P определяется углом поворота θ .

Пусть вектор координат точки P , определяющей точку опоры, равен r _P , и введем длины

a=|\mathbf {r} _{A}-\mathbf {r} _{P}|,\quad b=|\mathbf {r} _{B}-\mathbf {r} _{P}|,

которые представляют собой расстояния от точки опоры до входной точки A и до выходной точки B соответственно.

Теперь введем единичные векторы e _A и e _B от точки опоры до точки A и B , так что

\mathbf {r} _{A}-\mathbf {r} _{P}=a\mathbf {e} _{A},\quad \mathbf {r} _{B}-\mathbf {r} _{P}=b\mathbf {e} _{B}.

Эти обозначения позволяют определить скорость точек A и B как

\mathbf {v} _{A}={\dot {\theta }}a\mathbf {e} _{A}^{\perp },\quad \mathbf {v} _{B}={\dot {\theta }}b\mathbf {e} _{B}^{\perp },

где е _А^⊥ и е _Б^⊥ — единичные векторы, перпендикулярные e _A и e _B соответственно.

Угол θ является обобщенной координатой, определяющей конфигурацию рычага, поэтому, используя приведенную выше формулу для сил, приложенных к механизму с одной степенью свободы, обобщенная сила определяется выражением

Q=\mathbf {F} _{A}\cdot {\frac {\partial \mathbf {v} _{A}}{\partial {\dot {\theta }}}}-\mathbf {F} _{B}\cdot {\frac {\partial \mathbf {v} _{B}}{\partial {\dot {\theta }}}}=a(\mathbf {F} _{A}\cdot \mathbf {e} _{A}^{\perp })-b(\mathbf {F} _{B}\cdot \mathbf {e} _{B}^{\perp }).

Обозначим теперь через F _A и F _B составляющие сил, перпендикулярные радиальным отрезкам PA и PB . Эти силы задаются формулой

F_{A}=\mathbf {F} _{A}\cdot \mathbf {e} _{A}^{\perp },\quad F_{B}=\mathbf {F} _{B}\cdot \mathbf {e} _{B}^{\perp }.

Эти обозначения и принцип виртуальной работы дают формулу для обобщенной силы как

Q=aF_{A}-bF_{B}=0.

Отношение выходной силы F _B к входной силе F _A представляет собой механическое преимущество рычага и получается из принципа виртуальной работы как

MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}}.

Это уравнение показывает, что если расстояние a от точки опоры до точки A , к которой прилагается входная сила, больше, чем расстояние b от точки опоры до точки B , где прилагается выходная сила, то рычаг усиливает входную силу. Если верно обратное: расстояние от точки опоры до входной точки А меньше, чем от точки опоры до выходной точки В , то рычаг уменьшает величину входной силы.

Это закон рычага , который был доказан Архимедом с помощью геометрических рассуждений. ^[6]

Зубчатая передача [ править ]

Зубчатая передача образуется путем установки шестерен на раме так, чтобы зубья шестерен зацеплялись. Зубья шестерен предназначены для обеспечения качения делительных кругов шестерен сцепления друг о друга без проскальзывания, это обеспечивает плавную передачу вращения от одной шестерни к другой. Для этого анализа мы рассматриваем зубчатую передачу, имеющую одну степень свободы, что означает, что угловое вращение всех шестерен в зубчатой передаче определяется углом входной шестерни.

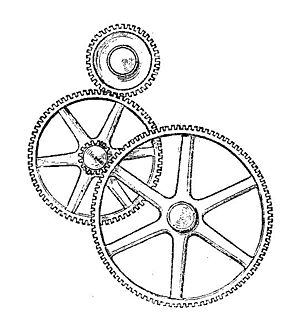
Размер шестерен и последовательность их включения определяют отношение угловой скорости ω _A входной шестерни к угловой скорости ω _B выходной шестерни, известное как передаточное число или передаточное число зубчатой передачи. . Пусть R — передаточное число, тогда

{\frac {\omega _{A}}{\omega _{B}}}=R.

Входной крутящий момент T _A, действующий на входную шестерню G _A, преобразуется зубчатой передачей в выходной крутящий момент T _B , создаваемый выходной шестерней G _B . Если предположить, что шестерни жесткие и потерь в зацеплении зубьев шестерен нет, то принцип виртуальной работы можно использовать для анализа статического равновесия зубчатой передачи.

Пусть угол θ входной шестерни является обобщенной координатой зубчатой передачи, тогда передаточное число R зубчатой передачи определяет угловую скорость выходной шестерни через входную шестерню, то есть

\omega _{A}=\omega ,\quad \omega _{B}=\omega /R.

Приведенная выше формула принципа виртуальной работы с приложенными крутящими моментами дает обобщенную силу

Q=T_{A}{\frac {\partial \omega _{A}}{\partial \omega }}-T_{B}{\frac {\partial \omega _{B}}{\partial \omega }}=T_{A}-T_{B}/R=0.

Механическое преимущество зубчатой передачи представляет собой отношение выходного крутящего момента T _B к входному крутящему моменту T _A , и приведенное выше уравнение дает

MA={\frac {T_{B}}{T_{A}}}=R.

Таким образом, передаточное число зубчатой передачи также определяет ее механическое преимущество. Это показывает, что если входная шестерня вращается быстрее, чем выходная, то зубчатая передача усиливает входной крутящий момент. А если входная шестерня вращается медленнее выходной, то зубчатая передача снижает входной крутящий момент.

Динамическое равновесие твердых тел [ править ]

Если принцип виртуальной работы приложенных сил применяется к отдельным частицам твердого тела , то этот принцип можно обобщить для твердого тела: когда твердое тело, находящееся в равновесии, подвергается виртуальным совместимым перемещениям, общая виртуальная работа всех внешние силы равны нулю; и наоборот, если общая виртуальная работа всех внешних сил, действующих на твердое тело, равна нулю, то тело находится в равновесии .

Если система не находится в статическом равновесии, Даламбер показал, что путем введения условий ускорения законов Ньютона в виде сил инерции этот подход обобщается для определения динамического равновесия. Результатом является форма принципа виртуальной работы Даламбера, которая используется для вывода уравнений движения механической системы твердых тел.

Выражение «совместимые смещения» означает, что частицы остаются в контакте и смещаются вместе, так что работа, совершаемая парами сил действия/противодействия между частицами, компенсируется. Различные формы этого принципа приписывались Иоганну (Жану) Бернулли (1667–1748) и Даниэлю Бернулли (1700–1782).

инерции Обобщенные силы

Пусть механическая система построена из n твердых тел B _i , i=1,...,n, и пусть результирующей приложенных сил к каждому телу являются пары сила- F _i и Ti _момент , i = 1,..., н . Обратите внимание, что эти приложенные силы не включают силы реакции в местах соединения тел. что скорость Vi _i и угловые скорости ω _, Наконец, предположим , i =1,..., n для каждого твердого тела определяются одной обобщенной координатой q. Говорят, что такая система твердых тел имеет одну степень свободы .

Рассмотрим одно твердое тело, которое движется под действием равнодействующей силы F и крутящего момента T с одной степенью свободы, определяемой обобщенной координатой q. Предположим, что точкой отсчета результирующей силы и крутящего момента является центр масс тела, тогда обобщенная сила инерции Q*, связанная с обобщенной координатой q, определяется выражением

Q^{*}=-(M\mathbf {A} )\cdot {\frac {\partial \mathbf {V} }{\partial {\dot {q}}}}-([I_{R}]\alpha +\omega \times [I_{R}]\omega )\cdot {\frac {\partial {\boldsymbol {\omega }}}{\partial {\dot {q}}}}.

Эту силу инерции можно вычислить по кинетической энергии твердого тела:

T={\frac {1}{2}}M\mathbf {V} \cdot \mathbf {V} +{\frac {1}{2}}{\boldsymbol {\omega }}\cdot [I_{R}]{\boldsymbol {\omega }},

используя формулу

Q^{*}=-\left({\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}}}-{\frac {\partial T}{\partial q}}\right).

Система n твердых тел с m обобщенными координатами имеет кинетическую энергию

T=\sum _{i=1}^{n}\left({\frac {1}{2}}M\mathbf {V} _{i}\cdot \mathbf {V} _{i}+{\frac {1}{2}}{\boldsymbol {\omega }}_{i}\cdot [I_{R}]{\boldsymbol {\omega }}_{i}\right),

который можно использовать для расчета m обобщенных сил инерции ^[7]

Q_{j}^{*}=-\left({\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right),\quad j=1,\ldots ,m.

Форма принципа виртуальной работы Даламбера [ править ]

Форма принципа виртуальной работы Даламбера гласит, что система твердых тел находится в динамическом равновесии, когда виртуальная работа суммы приложенных сил и сил инерции равна нулю при любом виртуальном перемещении системы. Таким образом, для динамического равновесия системы n твердых тел с m обобщенными координатами необходимо, чтобы

\delta W=(Q_{1}+Q_{1}^{*})\delta q_{1}+\dots +(Q_{m}+Q_{m}^{*})\delta q_{m}=0,

для любого набора виртуальных перемещений δq _j . Это условие дает m уравнений:

Q_{j}+Q_{j}^{*}=0,\quad j=1,\ldots ,m,

что также можно записать как

{\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}=Q_{j},\quad j=1,\ldots ,m.

В результате получается набор из m уравнений движения, определяющих динамику системы твердого тела, известный как уравнения Лагранжа или обобщенные уравнения движения .

Если обобщенные силы Q _j выводятся из потенциальной энергии V ( q ₁ ,..., q _m ), то эти уравнения движения принимают вид

{\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}=-{\frac {\partial V}{\partial q_{j}}},\quad j=1,\ldots ,m.

В этом случае введите лагранжиан = $L - T вид V$ , чтобы эти уравнения движения приняли

{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}-{\frac {\partial L}{\partial q_{j}}}=0\quad j=1,\ldots ,m.

Они известны как уравнения Эйлера-Лагранжа для системы с m степенями свободы или уравнения Лагранжа второго рода .

тела деформируемого Принцип виртуальной работы

Рассмотрим теперь диаграмму свободного тела деформируемого тела , состоящую из бесконечного числа дифференциальных кубов. Давайте определим два несвязанных состояния для тела:

The ${\boldsymbol {\sigma }}$ -Состояние: показывает внешние поверхностные силы T , объемные силы f и внутренние напряжения. ${\boldsymbol {\sigma }}$ в равновесии.
The ${\boldsymbol {\epsilon }}$ -State: показывает непрерывные перемещения. $\mathbf {u} ^{*}$ и постоянные штаммы ${\boldsymbol {\epsilon }}^{*}$ .

Верхний индекс * подчеркивает, что эти два состояния не связаны между собой. Помимо указанных выше условий, нет необходимости указывать, является ли какое-либо из состояний реальным или виртуальным.

Представьте теперь, что силы и напряжения в ${\boldsymbol {\sigma }}$ -государство претерпевает перемещения и деформации в ${\boldsymbol {\epsilon }}$ -Состояние: мы можем вычислить общую виртуальную (мнимую) работу, выполняемую всеми силами, действующими на гранях всех кубов, двумя разными способами:

Во-первых, суммируя работу, совершаемую такими силами, как $F_{A}$ которые действуют на отдельные общие грани (рис. в): Поскольку материал испытывает согласованные перемещения , такая работа компенсируется, оставляя только виртуальную работу, совершаемую поверхностными силами T (которые равны напряжениям на гранях кубов в равновесии) .
Во-вторых, вычисляя чистую работу, совершаемую напряжениями или силами, такими как $F_{A}$ , $F_{B}$ которые действуют на отдельный куб, например, для одномерного случая на рис. (c): $F_{B}\left(u^{*}+{\frac {\partial u^{*}}{\partial x}}dx\right)-F_{A}u^{*}\approx {\frac {\partial u^{*}}{\partial x}}\sigma dV+u^{*}{\frac {\partial \sigma }{\partial x}}dV=\epsilon ^{*}\sigma dV-u^{*}fdV$ где соотношение равновесия ${\frac {\partial \sigma }{\partial x}}+f=0$ использовался, а членом второго порядка пренебрегли.
Интеграция по всему телу дает: $\int _{V}{\boldsymbol {\epsilon }}^{*T}{\boldsymbol {\sigma }}\,dV$ – Работа, совершаемая массовыми силами f .

Приравнивание двух результатов приводит к принципу виртуальной работы деформируемого тела:

{\text{Total external virtual work}}=\int _{V}{\boldsymbol {\epsilon }}^{*T}{\boldsymbol {\sigma }}dV

( д )

где полная внешняя виртуальная работа выполняется T и f . Таким образом,

\int _{S}\mathbf {u} ^{*T}\mathbf {T} dS+\int _{V}\mathbf {u} ^{*T}\mathbf {f} dV=\int _{V}{\boldsymbol {\epsilon }}^{*T}{\boldsymbol {\sigma }}dV

( Это )

Правую часть ( d , e ) часто называют внутренней виртуальной работой. Тогда принцип виртуальной работы гласит: внешняя виртуальная работа равна внутренней виртуальной работе, когда уравновешенные силы и напряжения подвергаются несвязанным, но постоянным смещениям и деформациям . Он включает принцип виртуальной работы для твердых тел как частный случай, когда внутренняя виртуальная работа равна нулю.

Доказательство эквивалентности принципа виртуальной работы уравнения равновесия и

Начнем с рассмотрения общей работы, совершаемой поверхностным сцеплением тела, претерпевающего заданную деформацию:

\int _{S}\mathbf {u} \cdot \mathbf {T} dS=\int _{S}\mathbf {u} \cdot {\boldsymbol {\sigma }}\cdot \mathbf {n} dS

Применяя теорему о дивергенции к правой части, получаем:

\int _{S}\mathbf {u\cdot {\boldsymbol {\sigma }}\cdot n} dS=\int _{V}\nabla \cdot \left(\mathbf {u} \cdot {\boldsymbol {\sigma }}\right)dV

Теперь перейдем к указательным обозначениям для облегчения вывода.

{\begin{aligned}\int _{V}\nabla \cdot \left(\mathbf {u} \cdot {\boldsymbol {\sigma }}\right)dV&=\int _{V}{\frac {\partial }{\partial x_{j}}}\left(u_{i}\sigma _{ij}\right)dV\\&=\int _{V}\left({\frac {\partial u_{i}}{\partial x_{j}}}\sigma _{ij}+u_{i}{\frac {\partial \sigma _{ij}}{\partial x_{j}}}\right)dV\end{aligned}}

Для продолжения вывода подставим в уравнение равновесия ${\frac {\partial \sigma _{ij}}{\partial x_{j}}}+f_{i}=0$ . Затем

\int _{V}\left({\frac {\partial u_{i}}{\partial x_{j}}}\sigma _{ij}+u_{i}{\frac {\partial \sigma _{ij}}{\partial x_{j}}}\right)dV=\int _{V}\left({\frac {\partial u_{i}}{\partial x_{j}}}\sigma _{ij}-u_{i}f_{i}\right)dV

Первый член в правой части необходимо разбить на симметричную часть и косую часть следующим образом:

{\begin{aligned}\int _{V}\left({\frac {\partial u_{i}}{\partial x_{j}}}\sigma _{ij}-u_{i}f_{i}\right)dV&=\int _{V}\left({\frac {1}{2}}\left[\left({\frac {\partial u_{i}}{\partial x_{j}}}+{\frac {\partial u_{j}}{\partial x_{i}}}\right)+\left({\frac {\partial u_{i}}{\partial x_{j}}}-{\frac {\partial u_{j}}{\partial x_{i}}}\right)\right]\sigma _{ij}-u_{i}f_{i}\right)dV\\&=\int _{V}\left(\left[\epsilon _{ij}+{\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{j}}}-{\frac {\partial u_{j}}{\partial x_{i}}}\right)\right]\sigma _{ij}-u_{i}f_{i}\right)dV\\&=\int _{V}\left(\epsilon _{ij}\sigma _{ij}-u_{i}f_{i}\right)dV\\&=\int _{V}\left({\boldsymbol {\epsilon }}:{\boldsymbol {\sigma }}-\mathbf {u} \cdot \mathbf {f} \right)dV\end{aligned}}

где

{\boldsymbol {\epsilon }}

— деформация, соответствующая заданному полю смещений. Второе предпоследнее равенство обусловлено тем фактом, что матрица напряжений симметрична и что произведение асимметричной матрицы и симметричной матрицы равно нулю.

Теперь подведем итоги. С помощью приведенного выше вывода мы показали, что

\int _{S}\mathbf {u\cdot T} dS=\int _{V}{\boldsymbol {\epsilon }}:{\boldsymbol {\sigma }}dV-\int _{V}\mathbf {u} \cdot \mathbf {f} dV

Переместим второе слагаемое из правой части уравнения влево:

\int _{S}\mathbf {u\cdot T} dS+\int _{V}\mathbf {u} \cdot \mathbf {f} dV=\int _{V}{\boldsymbol {\epsilon }}:{\boldsymbol {\sigma }}dV

Физическая интерпретация приведенного выше уравнения такова: внешняя виртуальная работа равна внутренней виртуальной работе, когда уравновешенные силы и напряжения подвергаются несвязанным, но постоянным смещениям и деформациям .

Для практического применения:

Чтобы обеспечить равновесие реальных напряжений и сил, мы используем согласованные виртуальные перемещения и деформации в уравнении виртуальной работы.
Чтобы обеспечить согласованные перемещения и деформации, мы используем уравновешенные виртуальные напряжения и силы в уравнении виртуальной работы.

Эти два общих сценария порождают два часто упоминаемых вариационных принципа. Они действительны независимо от материального поведения.

Принцип виртуальных перемещений [ править ]

В зависимости от цели мы можем специализировать уравнение виртуальной работы. Например, чтобы вывести принцип виртуальных перемещений в вариационных обозначениях для опертых тел, укажем:

Виртуальные смещения и деформации как вариации реальных смещений и деформаций с использованием вариационных обозначений, таких как $\delta \ \mathbf {u} \equiv \mathbf {u} ^{*}$ и $\delta \ {\boldsymbol {\epsilon }}\equiv {\boldsymbol {\epsilon }}^{*}$
Виртуальные перемещения равны нулю на той части поверхности, на которой заданы перемещения, и, следовательно, работа, совершаемая реакциями, равна нулю. На детали остаются только внешние поверхностные силы $S_{t}$ это работает.

Тогда уравнение виртуальной работы становится принципом виртуальных перемещений:

\int _{S_{t}}\delta \ \mathbf {u} ^{T}\mathbf {T} dS+\int _{V}\delta \ \mathbf {u} ^{T}\mathbf {f} dV=\int _{V}\delta {\boldsymbol {\epsilon }}^{T}{\boldsymbol {\sigma }}dV

( ж )

Это соотношение эквивалентно системе уравнений равновесия, записанных для дифференциального элемента в деформируемом теле, а также напряженным граничным условиям на части $S_{t}$ поверхности. И наоборот, ( f ) можно достичь, хотя и нетривиальным способом, начав с дифференциальных уравнений равновесия и граничных условий напряжения на $S_{t}$ и действуя аналогично ( a ) и ( b ).

когда они выражаются через непрерывные Поскольку виртуальные смещения автоматически совместимы , однозначные функции , мы часто упоминаем только необходимость согласованности между деформациями и перемещениями. Принцип виртуальной работы справедлив и для больших реальных перемещений; однако тогда уравнение ( f ) будет записано с использованием более сложных показателей напряжений и деформаций.

Принцип виртуальных сил [ править ]

Здесь мы указываем:

Виртуальные силы и напряжения как вариации реальных сил и напряжений.
Виртуальные силы равны нулю на детали $S_{t}$ поверхности, на которой действуют предписанные силы, и, следовательно, только поверхностные (реакционные) силы на $S_{u}$ (где предписаны перемещения) будет работать.

Уравнение виртуальной работы становится принципом виртуальных сил:

\int _{S_{u}}\mathbf {u} ^{T}\delta \ \mathbf {T} dS+\int _{V}\mathbf {u} ^{T}\delta \ \mathbf {f} dV=\int _{V}{\boldsymbol {\epsilon }}^{T}\delta {\boldsymbol {\sigma }}dV

( г )

Это соотношение эквивалентно системе уравнений совместимости деформаций, а также граничных условий смещения на части $S_{u}$ . У него есть другое название: принцип дополняющей виртуальной работы.

формы Альтернативные

Специализацией принципа виртуальных сил является метод единичной фиктивной силы , который очень полезен для расчета смещений в структурных системах. Согласно принципу Даламбера , включение сил инерции в качестве дополнительных массовых сил даст уравнение виртуальной работы, применимое к динамическим системам. Более общие принципы могут быть выведены путем:

допуская вариации всех величин.
использование множителей Лагранжа для наложения граничных условий и/или смягчения условий, указанных в двух состояниях.

Они описаны в некоторых ссылках.

Среди многих энергетических принципов в строительной механике принцип виртуальной работы заслуживает особого места из-за своей общности, которая приводит к мощным приложениям в структурном анализе , механике твердого тела и методе конечных элементов в строительной механике .

См. также [ править ]

Ссылки [ править ]

^ Перейти обратно: ^а ^б К. Ланцос, Вариационные принципы механики, 4-е изд., General Publishing Co., Канада, 1970 г.
^ Дим, К. Л. и И. Х. Шеймс, Механика твердого тела: вариационный подход , McGraw-Hill, 1973.
^ Перейти обратно: ^а ^б ^с ^д ^Это Капечки, Данило (2012). История законов о виртуальной работе . Научные сети. Исторические исследования. Том. 42. Милан: Спрингер Милан. дои : 10.1007/978-88-470-2056-6 . ISBN 978-88-470-2055-9 .
^ Рене Дюга, История механики, Courier Corporation, 2012 г.
^ Т.Р. Кейн и Д.А. Левинсон, Динамика: теория и приложения, McGraw-Hill, Нью-Йорк, 1985.
^ Ашер, AP (1929). История механических изобретений . Издательство Гарвардского университета (перепечатано Dover Publications, 1988 г.). п. 94. ИСБН 978-0-486-14359-0 . OCLC 514178 . Проверено 7 апреля 2013 г.
^ Т.Р. Кейн и Д.А. Левинсон, Динамика, теория и приложения , МакГроу-Хилл, Нью-Йорк, 2005.

Внешние ссылки [ править ]

Примеры применения принципа виртуальной работы

Библиография [ править ]

Бат, К.Дж. «Процедуры конечных элементов», Прентис Холл, 1996. ISBN 0-13-301458-4
Чарльтон, Энергетические принципы ТМ в теории конструкций , Oxford University Press, 1973. ISBN 0-19-714102-1
Дайм, К. Л. и И. Х. Шеймс, Механика твердого тела: вариационный подход , McGraw-Hill, 1973.
Гринвуд, Дональд Т. Классическая динамика , Dover Publications Inc., 1977, ISBN 0-486-69690-1
Ху, Х. Вариационные принципы теории упругости с приложениями , Тейлор и Фрэнсис, 1984. ISBN 0-677-31330-6
Лангхаар, Х.Л. Энергетические методы в прикладной механике , Кригер, 1989.
Редди, Дж. Н. Энергетические принципы и вариационные методы в прикладной механике , Джон Уайли, 2002. ISBN 0-471-17985-X
Шамс, И.Х. и Дайм, К.Л. Энергия и методы конечных элементов в структурной механике , Тейлор и Фрэнсис, 1995, ISBN 0-89116-942-3
Таучерт, Т.Р. Энергетические принципы в строительной механике , McGraw-Hill, 1974. ISBN 0-07-062925-0
Васизу, К. Вариационные методы упругости и пластичности , Pergamon Pr, 1982. ISBN 0-08-026723-8
Вундерлих, В. Механика конструкций: вариационные и вычислительные методы , CRC, 2002. ISBN 0-8493-0700-7

[Lanczos-1] Перейти обратно: ^а ^б К. Ланцос, Вариационные принципы механики, 4-е изд., General Publishing Co., Канада, 1970 г.

[2] Дим, К. Л. и И. Х. Шеймс, Механика твердого тела: вариационный подход , McGraw-Hill, 1973.

[capecchi-3] Перейти обратно: ^а ^б ^с ^д ^Это Капечки, Данило (2012). История законов о виртуальной работе . Научные сети. Исторические исследования. Том. 42. Милан: Спрингер Милан. дои : 10.1007/978-88-470-2056-6 . ISBN 978-88-470-2055-9 .

[dugas-4] Рене Дюга, История механики, Courier Corporation, 2012 г.

[5] Т.Р. Кейн и Д.А. Левинсон, Динамика: теория и приложения, McGraw-Hill, Нью-Йорк, 1985.

[Usher1954-6] Ашер, AP (1929). История механических изобретений . Издательство Гарвардского университета (перепечатано Dover Publications, 1988 г.). п. 94. ИСБН 978-0-486-14359-0 . OCLC 514178 . Проверено 7 апреля 2013 г.

[7] Т.Р. Кейн и Д.А. Левинсон, Динамика, теория и приложения , МакГроу-Хилл, Нью-Йорк, 2005.

[1]

[2]

[3]

[4]

[5]

[6]

[7]