Список вероятностных распределений

Многим распределениям вероятностей , важным в теории или приложениях, были даны конкретные названия.

распределения

Биномиальное распределение

Вырожденное распределение

С ограниченной поддержкой

• Распределение Бернулли , которое принимает значение 1 с вероятностью p и значение 0 с вероятностью q = 1 − p .
• Распределение Радемахера , которое принимает значение 1 с вероятностью 1/2 и значение −1 с вероятностью 1/2.
• Биномиальное распределение , которое описывает количество успехов в серии независимых экспериментов «да/нет» с одинаковой вероятностью успеха.
• Бета -биномиальное распределение , которое описывает количество успехов в серии независимых экспериментов «да/нет» с неоднородностью вероятности успеха.
• Вырожденное распределение в точке , _x0 где X наверняка примет x0 _{значение} . Это не выглядит случайным, но удовлетворяет определению случайной величины . Это полезно, поскольку помещает детерминированные переменные и случайные величины в один и тот же формализм.
• Дискретное равномерное распределение , при котором все элементы конечного множества равновероятны. Это теоретическая модель распределения сбалансированной монеты, беспристрастной кости, рулетки казино или первой карты хорошо перетасованной колоды.
• Гипергеометрическое распределение , которое описывает количество успехов в первых m серии из n последовательных экспериментов Да/Нет, если известно общее количество успехов. Такое распределение возникает, когда нет замены.
• Отрицательное гипергеометрическое распределение — распределение, которое описывает количество попыток, необходимых для достижения n- го успеха в серии экспериментов «Да/Нет» без замены.
• , Биномиальное распределение Пуассона которое описывает количество успехов в серии независимых экспериментов «да/нет» с разными вероятностями успеха.
• Нецентральное гипергеометрическое распределение Фишера
• Нецентральное гипергеометрическое распределение Валлениуса
• Закон Бенфорда , который описывает частоту первой цифры многих природных данных.
• Идеальные и робастные солитонные распределения .
• Закон Ципфа или распределение Ципфа. Дискретное степенное распределение , самым известным примером которого является описание частотности слов в английском языке.
• Закон Ципфа – Мандельброта представляет собой дискретное степенное распределение, которое является обобщением распределения Ципфа.

Распределение Конвея – Максвелла – Пуассона

Распределение Пуассона

Распространение Скеллама

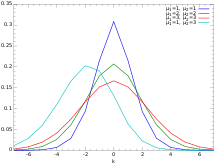
С бесконечной поддержкой

• Бета -отрицательное биномиальное распределение
• Распределение Больцмана — дискретное распределение, важное в статистической физике , которое описывает вероятности различных дискретных уровней энергии системы, находящейся в тепловом равновесии . Имеет непрерывный аналог. К особым случаям относятся:
  • Гиббса Распределение
  • Распределение Максвелла – Больцмана.
• Бореля Распределение
• Распределение дискретного фазового типа — обобщение геометрического распределения, которое описывает момент первого попадания в поглощающее состояние конечной завершающейся цепи Маркова .
• Расширенное отрицательное биномиальное распределение
• Обобщенное распределение логарифмических рядов
• Кузьмина Распределение Гаусса –
• Геометрическое распределение — дискретное распределение, которое описывает количество попыток, необходимых для достижения первого успеха в серии независимых испытаний Бернулли, или, альтернативно, только количество потерь до первого успеха (т. е. на одну меньше).
• Эрмита Распределение
• Логарифмическое (рядовое) распределение
• Смешанное распределение Пуассона
• Отрицательное биномиальное распределение или распределение Паскаля, обобщение геометрического распределения до n -го успеха.
• Дискретное составное распределение Пуассона
• Параболическое фрактальное распределение
• Распределение Пуассона , которое описывает очень большое количество индивидуально маловероятных событий, происходящих в определенном интервале времени. С этим распределением связан ряд других распределений: смещенное распределение Пуассона , гиперпуассоновое, общее биномиальное распределение Пуассона и распределения типа Пуассона.
  • Распределение Конвея -Максвелла-Пуассона , двухпараметрическое расширение распределения Пуассона с регулируемой скоростью затухания.
  • Распределение Пуассона, усеченное до нуля , для процессов, в которых нулевые значения не наблюдаются.
• The Polya–Eggenberger distribution
• Распределение Скеллама — распределение разницы между двумя независимыми случайными величинами, распределенными по Пуассону.
• Перекос эллиптического распределения
• Распределение Юла – Саймона
• Дзета -распределение находит применение в прикладной статистике и статистической механике и, возможно, может представлять интерес для теоретиков чисел. Это распределение Ципфа для бесконечного числа элементов.
• Распределение Харди , которое описывает вероятности очков на лунках для данного игрока в гольф.

Абсолютно непрерывные распределения

Бета-дистрибутив

Распределение Кумарасвами

Непрерывное равномерное распределение

Поддерживается на ограниченном интервале

• Бета -распределение на [0,1], семейство двухпараметрических распределений с одной модой, частным случаем которого является равномерное распределение и которое полезно при оценке вероятностей успеха.
  • Бета -распределение с четырьмя параметрами — прямое обобщение бета-распределения на произвольные ограниченные интервалы. $[a,b]$.
• Арксинусное распределение на [ a , b ], которое является частным случаем бета-распределения, если α = β = 1/2, a = 0 и b = 1.
• Распределение PERT является частным случаем четырехпараметрического бета-распределения .
• Равномерное распределение или прямоугольное распределение на [ a , b ], где все точки в конечном интервале равновероятны, является частным случаем четырехпараметрического бета-распределения.
• Распределение Ирвина-Холла представляет собой распределение суммы n независимых случайных величин, каждая из которых имеет равномерное распределение на [0,1].
• Распределение Бейтса — это распределение среднего значения n независимых случайных величин, каждая из которых имеет равномерное распределение на [0,1].
• Логит -нормальное распределение на (0,1).
• Дельта- функция Дирака , хотя и не является строго распределением вероятностей, является предельной формой многих непрерывных функций вероятности. Оно представляет собой дискретное распределение вероятностей, сосредоточенное в точке 0 — вырожденное распределение — это Распределение (математика) в смысле обобщенной функции; но обозначения трактуют его так, как если бы это было непрерывное распределение.
• на Распределение Кента двумерной сфере.
• Дистрибутив Kumaraswamy так же универсален, как и бета-дистрибутив, но имеет простые закрытые формы как для CDF, так и для PDF.
• Распределение логит-металог , которое отличается высокой гибкостью формы, имеет простые замкнутые формы и может быть параметризовано данными с использованием линейного метода наименьших квадратов.
• Распределение Марченко-Пастура играет важную роль в теории случайных матриц .
• Ограниченные распределения, параметризованные квантилем , которые обладают высокой гибкостью формы и могут быть параметризованы данными с использованием линейного метода наименьших квадратов (см. Распределение, параметризованное квантилем#Преобразования ).
• Распределение приподнятого косинуса на [ $\mu -s,\mu +s$]
• распределение Взаимное
• Треугольное распределение на [ a , b ], частным случаем которого является распределение суммы двух независимых равномерно распределенных случайных величин ( свертка двух равномерных распределений).
• Трапециевидное распределение
• Усеченное нормальное распределение на [ a , b ].
• U -квадратичное распределение на [ a , b ].
• Распределение фон Мизеса-Фишера на N -мерной сфере имеет распределение фон Мизеса как частный случай.
• на Распределение Бингама N - мерной сфере.
• Распределение полукруга Вигнера играет важную роль в теории случайных матриц .
• Непрерывное распределение Бернулли представляет собой однопараметрическое экспоненциальное семейство , которое обеспечивает вероятностный аналог двоичной кросс-энтропийной потери.

Распределение хи-квадрат

Гамма-распределение

Распределение Парето

Поддерживается на интервалах длиной 2 π – направленные распределения

• Гринштейна Фазовая функция Хеньи –
• Фазовая функция Ми
• Распределение фон Мизеса
• Обернутое нормальное распределение
• Обернутое экспоненциальное распределение
• Обернутое распределение Леви
• Обернутое распределение Коши
• Завернутое распределение Лапласа
• Обернутое асимметричное распределение Лапласа
• Гребень Дирака периода 2 π , хотя и не является строго функцией, является предельной формой многих распределений по направлениям. По сути, это завернутая дельта-функция Дирака . Оно представляет собой дискретное распределение вероятностей, сосредоточенное в точке 2 π n — вырожденное распределение — но в обозначениях оно рассматривается так, как если бы оно было непрерывным распределением.

Поддерживается на полубесконечных интервалах, обычно [0,∞)

• Бета -простое распределение
• Распределение Бирнбаума -Сондерса , также известное как распределение усталостной долговечности, представляет собой распределение вероятностей, широко используемое в приложениях, связанных с надежностью, для моделирования времени отказов.
• Распределение ци
  • Нецентральное распределение ци
• Распределение хи-квадрат , которое представляет собой сумму квадратов n независимых гауссовских случайных величин. Это частный случай гамма-распределения, который используется в тестах согласия в статистике .
  • Распределение обратного хи-квадрата
  • Нецентральное распределение хи-квадрат
  • Масштабированное обратное распределение хи-квадрат
• Дагума Распределение
• Экспоненциальное распределение , которое описывает время между последовательными редкими случайными событиями в процессе без памяти.
• Экспоненциально -логарифмическое распределение
• F -распределение , которое представляет собой распределение отношения двух (нормализованных) случайных величин с распределением хи-квадрат, используемое в дисперсионном анализе . Его называют бета-распределением простых чисел , когда оно представляет собой отношение двух переменных хи-квадрат, которые не нормализуются путем деления их на количество степеней свободы.
  • Нецентральное F-распределение
• Свернутое нормальное распределение
• Распределение Фреше
• Гамма -распределение , которое описывает время, пока n в процессе без памяти не произойдет последовательных редких случайных событий.
  • Распределение Эрланга , которое является частным случаем гамма-распределения с интегральным параметром формы, разработанным для прогнозирования времени ожидания в системах массового обслуживания.
  • Обратное гамма-распределение
• Обобщенное гамма-распределение
• Обобщенное распределение Парето
• Распределение Гамма /Гомпертца
• Гомпертца Распределение
• Полунормальное распределение
• Распределение Хотеллинга Т-квадрат
• Обратное распределение Гаусса , также известное как распределение Вальда.
• Распределение Леви
• Распределение лог -Коши
• Логарифмическое распределение Лапласа
• Логистически -логистическое распределение
• Логарифмическое металогарифмическое распределение отличается высокой гибкостью формы, имеет простые замкнутые формы, может быть параметризовано данными с использованием линейного метода наименьших квадратов и включает логарифмическое логистическое распределение как особый случай.
• Логнормальное распределение , описывающее переменные, которые можно смоделировать как произведение множества небольших независимых положительных переменных.
• Ломакса Распределение
• Леффлера Распределение Миттаг-
• Распределение Накагами
• Распределение Парето , или распределение «степенного закона», используемое при анализе финансовых данных и критического поведения.
• Распределение Пирсона типа III
• Распределение фазового типа , используемое в теории массового обслуживания
• Поэтапное биэкспоненциальное распределение обычно используется в фармакокинетике.
• Поэтапное распределение би-Вейбулла
• Полуограниченные распределения, параметризованные квантилем , которые обладают высокой гибкостью формы и могут быть параметризованы данными с использованием линейного метода наименьших квадратов (см. Распределение, параметризованное квантилем § Преобразования).
• Рэлея Распределение
• Распределение смеси Рэлея
• Распределение риса
• Смещенное распределение Гомпертца
• 2 Распределение Гамбеля типа
• Распределение Вейбулла или распределение Розина-Раммлера, частным случаем которого является экспоненциальное распределение , используется для моделирования срока службы технических устройств и используется для описания гранулометрического состава частиц, образующихся в результате операций измельчения, измельчения и дробления .
• Модифицированное полунормальное распределение .
• The Polya-Gamma distribution
• Модифицированное распределение Поля-гамма .

Распределение Коши

Распределение Джонсона SU

Распределение Лапласа

Стабильное распространение

Поддерживается на всей линии

• Распределение Беренса -Фишера , возникающее в задаче Беренса-Фишера .
• Распределение Коши , пример распределения, которое не имеет ожидаемого значения или дисперсии . В физике его обычно называют лоренцевым профилем , и он связан со многими процессами, включая резонансное распределение энергии, ударное и естественное уширение спектральных линий , а также квадратичное уширение штарковских линий.
• Централизованное обратное распределение Фано , которое представляет собой соотношение независимых нормальных и гамма-разностных случайных величин.
• Распределение Чернова
• Экспоненциально модифицированное распределение Гаусса , свертка нормального распределения с экспоненциальным распределением , и гауссово минус экспоненциальное распределение , свертка нормального распределения с отрицательным экспоненциальным распределением.
• Распределение ожиданий , которое в симметричном случае вкладывает в распределение Гаусса.
• Распределение Фишера -Типпета , экстремальное значение или логарифмическое распределение Вейбулла.
• Z-распределение Фишера
• Искаженное обобщенное распределение t
• Распределение гамма-разности , которое представляет собой распределение разности независимых гамма-случайных величин.
• Обобщенное логистическое распределение
• Обобщенное нормальное распределение
• Геометрическое стабильное распределение
• Распределение Гамбеля
• — Распределение Хольцмарка пример распределения, которое имеет конечное ожидаемое значение, но бесконечную дисперсию.
• Гиперболическое распределение
• Гиперболическое секущее распределение
• Распределение Джонсона SU
• Ландау Распределение
• Лапласа Распределение
• или Скошенное альфа-стабильное распределение Леви стабильное распределение — это семейство распределений, которое часто используется для характеристики финансовых данных и критического поведения; распределение Коши , распределение Хольцмарка , распределение Ландау , распределение Леви и нормальное распределение являются особыми случаями.
• Линника Распределение
• Логистическое распределение
• Карта -распределение Эйри
• Распределение металога , которое отличается высокой гибкостью формы, имеет простые замкнутые формы и может быть параметризовано данными с использованием линейного метода наименьших квадратов.
• Нормальное распределение , также называемое гауссовым или колоколообразной кривой. Он повсеместно встречается в природе и статистике благодаря центральной предельной теореме : каждая переменная, которую можно смоделировать как сумму многих небольших независимых, одинаково распределенных переменных с конечным средним значением и дисперсией, является приблизительно нормальной.
• Нормально -экспоненциальное гамма-распределение
• Нормально -обратное распределение Гаусса
• Распределение Пирсона типа IV (см. Распределения Пирсона )
• Распределения , параметризованные квантилем , которые обладают высокой гибкостью формы и могут быть параметризованы данными с использованием линейного метода наименьших квадратов.
• Перекос нормального распределения
• Т-распределение Стьюдента , полезное для оценки неизвестных средних значений гауссовских популяций.
  • Нецентральное t-распределение
  • Неравномерное распределение
• Распределение Чампернауна
• Распределение Гамбеля типа 1
• Распределение Трейси – Уидома
• Распределение Фойгта , или профиль Фойгта, представляет собой свертку нормального распределения и распределения Коши . Это обнаруживается в спектроскопии, когда профили спектральных линий уширяются за счет смеси механизмов лоренцева и доплеровского уширения .
• Распределение Чена .

С поддержкой переменных

• Обобщенное распределение экстремальных значений имеет конечную верхнюю границу или конечную нижнюю границу в зависимости от того, в каком диапазоне находится значение одного из параметров распределения (или поддерживается на всей вещественной линии для одного специального значения параметра
• Обобщенное распределение Парето имеет основу, ограниченную либо только снизу, либо ограниченную как сверху, так и снизу.
• Распределение металога , которое обеспечивает гибкость для неограниченной, ограниченной и полуограниченной поддержки, обладает высокой гибкостью формы, имеет простые замкнутые формы и может быть адаптировано к данным с использованием линейного метода наименьших квадратов.
• Лямбда- распределение Тьюки поддерживается либо на всей вещественной строке, либо на ограниченном интервале, в зависимости от того, в каком диапазоне находится значение одного из параметров распределения.
• Распределение Уэйкби

дискретные/

• Выпрямленное распределение Гаусса заменяет отрицательные значения нормального распределения дискретной составляющей в нуле.
• Составное распределение Пуассона-гаммы или распределение Твиди непрерывно по строго положительным действительным числам с нулевой массой.

Совместные дистрибутивы

Для любого набора независимых случайных величин функция плотности вероятности их совместного распределения является произведением их индивидуальных функций плотности.

Две или более случайные величины в одном пространстве выборки

• Распределение Дирихле — обобщение бета-распределения .
• представляет Формула выборки Юэнса собой распределение вероятностей на множестве всех частей целого числа n , возникающее в популяционной генетике .
• Модель Болдинга-Николса
• Полиномиальное распределение — обобщение биномиального распределения .
• Многомерное нормальное распределение — обобщение нормального распределения .
• Многомерное t-распределение , обобщение t-распределения Стьюдента .
• Отрицательное полиномиальное распределение — обобщение отрицательного биномиального распределения .
• , Отрицательное полиномиальное распределение Дирихле обобщение бета-отрицательного биномиального распределения .
• Обобщенное многомерное лог-гамма-распределение
• Экспоненциальное распределение Маршалла – Олкина
• Непрерывно -категорическое распределение — экспоненциальное семейство , поддерживаемое на симплексе , который обобщает непрерывное распределение Бернулли .

матричных

• Уишарта Распределение
• Обратное распределение Уишарта
• Распределение Левандовского -Куровицки-Джо.
• Матричное нормальное распределение
• Матричное t-распределение
• Ланжевена Распределение матрицы
• Матричное вариативное бета-распределение

Нечисловые распределения

• Категориальное распределение

Разные дистрибутивы

• Кантора Распределение
• Семейство обобщенной логистической дистрибуции
• Семейство металогов дистрибутивов
• Семья Пирсонов дистрибьюторов
• типа Распределение фазового

См. также

• Распределение смеси
• Отношения между распределениями вероятностей
• ПробОнто