Джонсона S U -распределение

Джонсонс С _У

Функция плотности вероятности
Кумулятивная функция распределения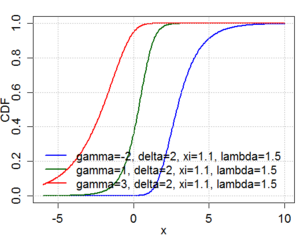
Параметры	$\gamma ,\xi ,\delta >0,\lambda >0$ ( настоящий )
Поддерживать	$-\infty {\text{ to }}+\infty$
PDF	${\frac {\delta }{\lambda {\sqrt {2\pi }}}}{\frac {1}{\sqrt {1+\left({\frac {x-\xi }{\lambda }}\right)^{2}}}}e^{-{\frac {1}{2}}\left(\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)\right)^{2}}$
CDF	$\Phi \left(\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)\right)$
Иметь в виду	$\xi -\lambda \exp {\frac {\delta ^{-2}}{2}}\sinh \left({\frac {\gamma }{\delta }}\right)$
медиана	$\xi +\lambda \sinh \left(-{\frac {\gamma }{\delta }}\right)$
Дисперсия	${\frac {\lambda ^{2}}{2}}(\exp(\delta ^{-2})-1)\left(\exp(\delta ^{-2})\cosh \left({\frac {2\gamma }{\delta }}\right)+1\right)$
асимметрия	$-{\frac {\lambda ^{3}{\sqrt {e^{\delta ^{-2}}}}(e^{\delta ^{-2}}-1)^{2}((e^{\delta ^{-2}})(e^{\delta ^{-2}}+2)\sinh({\frac {3\gamma }{\delta }})+3\sinh({\frac {2\gamma }{\delta }}))}{4(\operatorname {Variance} X)^{1.5}}}$
Избыточный эксцесс	${\frac {\lambda ^{4}(e^{\delta ^{-2}}-1)^{2}(K_{1}+K_{2}+K_{3})}{8(\operatorname {Variance} X)^{2}}}$ $K_{1}=\left(e^{\delta ^{-2}}\right)^{2}\left(\left(e^{\delta ^{-2}}\right)^{4}+2\left(e^{\delta ^{-2}}\right)^{3}+3\left(e^{\delta ^{-2}}\right)^{2}-3\right)\cosh \left({\frac {4\gamma }{\delta }}\right)$ $K_{2}=4\left(e^{\delta ^{-2}}\right)^{2}\left(\left(e^{\delta ^{-2}}\right)+2\right)\cosh \left({\frac {3\gamma }{\delta }}\right)$ $K_{3}=3\left(2\left(e^{\delta ^{-2}}\right)+1\right)$

Джонсона впервые SU _- распределение — это четырехпараметрическое семейство вероятностных распределений, исследованное Н. Л. Джонсоном в 1949 году. Джонсон предложил это как преобразование нормального распределения :

$z=\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)$

где $z\sim {\mathcal {N}}(0,1)$.

Генерация случайных величин

Пусть U — случайная величина , равномерно распределенная на единичном интервале [0, 1]. могут быть _{Джонсона SU} Случайные величины сгенерированы из U следующим образом:

$x=\lambda \sinh \left({\frac {\Phi ^{-1}(U)-\gamma }{\delta }}\right)+\xi$

где Φ — кумулятивная функция распределения нормального распределения .

Джонсона SB _{распределение} -

Н.Л. Джонсон сначала предлагает преобразование:

$z=\gamma +\delta \log \left({\frac {x-\xi }{\xi +\lambda -x}}\right)$

где $z\sim {\mathcal {N}}(0,1)$.

могут быть _{Джонсона SB} Случайные величины сгенерированы из U следующим образом:

$y={\left(1+{e}^{-\left(z-\gamma \right)/\delta }\right)}^{-1}$

$x=\lambda y+\xi$

S Куртозис _B -распределение удобно для распределений Платикуртика ( ) .Для моделирования SU _здесь образец кода для его плотности и кумулятивной функции распределения доступен .

Приложения

Джонсонс $S_{U}$-распределение успешно использовалось для моделирования доходности активов для управления портфелем . Это является превосходной альтернативой использованию нормального распределения для моделирования доходности активов. Пакет R JSUparameters . был разработан в 2021 году для помощи в оценке параметров наиболее подходящего метода Джонсона $S_{U}$-распределение для данного набора данных. Распределения Джонсона также иногда используются при ценообразовании опционов , чтобы учесть наблюдаемую волатильность ; см. биномиальное дерево Джонсона .

Альтернативой системе распределений Джонсона являются квантильно-параметризованные распределения (QPD). QPD могут обеспечить большую гибкость формы, чем система Джонсона. Вместо подбора моментов QPD обычно соответствуют эмпирическим данным CDF с помощью линейного метода наименьших квадратов.

Джонсонс $S_{U}$-распределение также используется при моделировании инвариантной массы некоторых тяжелых мезонов в области B-физики .

Дальнейшее чтение

• Хилл, ID; Хилл, Р.; Холдер, Р.Л. (1976). «Алгоритм AS 99: подгонка кривых Джонсона по моментам». Журнал Королевского статистического общества. Серия C (Прикладная статистика) . 25 (2).
• Джонс, MC; Пьюси, А. (2009). «Распределения Синх-Арксинх» (PDF) . Биометрика . 96 (4): 761. doi : 10.1093/biomet/asp053 . ( Препринт )
• Туэнтер, Ханс Дж. Х. (ноябрь 2001 г.). «Алгоритм определения параметров SU _{-кривых} в системе вероятностных распределений Джонсона методом согласования моментов». Журнал статистических вычислений и моделирования . 70 (4): 325–347. дои : 10.1080/00949650108812126 . МР   1872992 . Збл   1098.62523 .