q - Распределение Вейбулла

q - Распределение Вейбулла

Функция плотности вероятности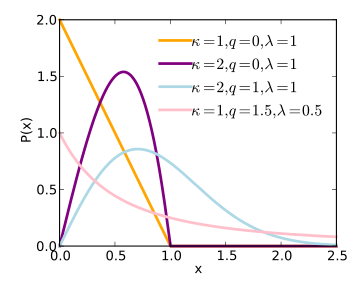
Кумулятивная функция распределения
Параметры	$q<2$ форма ( настоящая ) $\lambda >0$ ставка ( реальная ) $\kappa >0\,$ форма (настоящая)
Поддерживать	$x\in [0;+\infty )\!{\text{ for }}q\geq 1$ $x\in [0;{\lambda \over {(1-q)^{1/\kappa }}}){\text{ for }}q<1$
PDF	${\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}^{-(x/\lambda )^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$
CDF	${\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$
Иметь в виду	(см. статью)

В статистике q -распределение Вейбулла представляет собой распределение вероятностей , которое обобщает распределение Вейбулла и распределение Ломакса (тип Парето II). Это один из примеров распределения Цаллиса .

Характеристика

Функция плотности вероятности

Функция плотности вероятности Вейбулла q - случайной величины :

$f(x;q,\lambda ,\kappa )={\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}(-(x/\lambda )^{\kappa })&x\geq 0,\\0&x<0,\end{cases}}$

где q < 2, $\kappa$ > 0 — параметры формы , λ > 0 — параметр масштаба распределения и

$e_{q}(x)={\begin{cases}\exp(x)&{\text{if }}q=1,\\[6pt][1+(1-q)x]^{1/(1-q)}&{\text{if }}q\neq 1{\text{ and }}1+(1-q)x>0,\\[6pt]0^{1/(1-q)}&{\text{if }}q\neq 1{\text{ and }}1+(1-q)x\leq 0,\\[6pt]\end{cases}}$

является q -экспонентой

Кумулятивная функция распределения

Кумулятивная функция распределения равна q - случайной величины Вейбулла :

${\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$

где

$\lambda '={\lambda \over (2-q)^{1 \over \kappa }}$

$q'={1 \over (2-q)}$

Иметь в виду

Среднее значение q -распределения Вейбулла равно

$\mu (q,\kappa ,\lambda )={\begin{cases}\lambda \,\left(2+{\frac {1}{1-q}}+{\frac {1}{\kappa }}\right)(1-q)^{-{\frac {1}{\kappa }}}\,B\left[1+{\frac {1}{\kappa }},2+{\frac {1}{1-q}}\right]&q<1\\\lambda \,\Gamma (1+{\frac {1}{\kappa }})&q=1\\\lambda \,(2-q)(q-1)^{-{\frac {1+\kappa }{\kappa }}}\,B\left[1+{\frac {1}{\kappa }},-\left(1+{\frac {1}{q-1}}+{\frac {1}{\kappa }}\right)\right]&1<q<1+{\frac {1+2\kappa }{1+\kappa }}\\\infty &1+{\frac {\kappa }{\kappa +1}}\leq q<2\end{cases}}$

где $B()$ это бета-функция и $\Gamma ()$ это гамма-функция . Выражение среднего значения является непрерывной функцией q в диапазоне определения, для которого оно конечно.

Связь с другими дистрибутивами

q - Вейбулла эквивалентно распределению Вейбулла, когда q = 1, и эквивалентно q -экспоненте, когда $\kappa =1$

q -Вейбулла является обобщением распределения Вейбулла, поскольку оно расширяет это распределение на случаи конечного носителя ( q < 1) и включает распределения с тяжелым хвостом. $(q\geq 1+{\frac {\kappa }{\kappa +1}})$.

q - Вейбулл является обобщением распределения Ломакса (тип Парето II), поскольку оно расширяет это распределение на случаи конечной поддержки и добавляет $\kappa$ параметр. Параметры Ломакса:

$\alpha ={{2-q} \over {q-1}}~,~\lambda _{\text{Lomax}}={1 \over {\lambda (q-1)}}$

Поскольку распределение Ломакса представляет собой сдвинутую версию распределения Парето , q -Вейбулла для $\kappa =1$ представляет собой сдвинутое репараметризованное обобщение Парето. Когда q > 1, q -экспонента эквивалентна сдвигу Парето, чтобы поддержка начиналась с нуля. Конкретно:

${\text{If }}X\sim \operatorname {{\mathit {q}}-Weibull} (q,\lambda ,\kappa =1){\text{ and }}Y\sim \left[\operatorname {Pareto} \left(x_{m}={1 \over {\lambda (q-1)}},\alpha ={{2-q} \over {q-1}}\right)-x_{m}\right],{\text{ then }}X\sim Y\,$

См. также

• Константино Цаллис
• Статистика Цаллиса
• Энтропия Цаллиса
• Распространение Цаллиса
• q - Гауссова