Распределение Фреше

Фреше

Функция плотности вероятности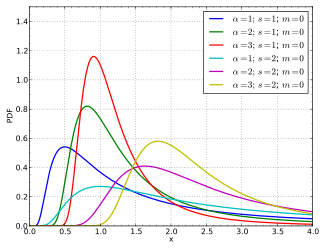
Кумулятивная функция распределения
Параметры	$\alpha \in (0,\infty )$ форма . (Необязательно, еще два параметра) $s\in (0,\infty )$ масштаб (по умолчанию: $s=1\,$) $m\in (-\infty ,\infty )$ местоположение минимума (по умолчанию: $m=0\,$)
Поддерживать	$x>m$
PDF	${\frac {\alpha }{s}}\;\left({\frac {x-m}{s}}\right)^{-1-\alpha }\;e^{-({\frac {x-m}{s}})^{-\alpha }}$
CDF	$e^{-({\frac {x-m}{s}})^{-\alpha }}$
Квантиль	$\left(-\ln(p)\right)^{-{\frac {1}{\alpha }}}$
Иметь в виду	${\begin{cases}\ m+s\Gamma \left(1-{\frac {1}{\alpha }}\right)&{\text{for }}\alpha >1\\\ \infty &{\text{otherwise}}\end{cases}}$
медиана	$m+{\frac {s}{\sqrt[{\alpha }]{\log _{e}(2)}}}$
Режим	$m+s\left({\frac {\alpha }{1+\alpha }}\right)^{1/\alpha }$
Дисперсия	${\begin{cases}\ s^{2}\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\left(\Gamma \left(1-{\frac {1}{\alpha }}\right)\right)^{2}\right)&{\text{for }}\alpha >2\\\ \infty &{\text{otherwise}}\end{cases}}$
асимметрия	${\begin{cases}\ {\frac {\Gamma \left(1-{\frac {3}{\alpha }}\right)-3\Gamma \left(1-{\frac {2}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+2\Gamma ^{3}\left(1-{\frac {1}{\alpha }}\right)}{\sqrt {\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right)^{3}}}}&{\text{for }}\alpha >3\\\ \infty &{\text{otherwise}}\end{cases}}$
Избыточный эксцесс	${\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{for }}\alpha >4\\\ \infty &{\text{otherwise}}\end{cases}}$
Энтропия	$1+{\frac {\gamma }{\alpha }}+\gamma +\ln \left({\frac {s}{\alpha }}\right)$, где $\gamma$ – постоянная Эйлера–Машерони .
МГФ	Примечание: Момент $k$ существует, если $\alpha >k$
CF

Распределение Фреше , также известное как обратное распределение Вейбулла , является частным случаем обобщенного распределения экстремальных значений . Имеет кумулятивную функцию распределения

$\Pr(X\leq x)=e^{-x^{-\alpha }}{\text{ if }}x>0.$

где α > 0 — параметр формы . Его можно обобщить, включив в него параметр местоположения m (минимум) и параметр масштаба s > 0 с кумулятивной функцией распределения.

$\Pr(X\leq x)=e^{-\left({\frac {x-m}{s}}\right)^{-\alpha }}{\text{ if }}x>m.$

Назван в честь Мориса Фреше , написавшего соответствующую статью в 1927 году. дальнейшая работа была проделана Фишером и Типпеттом в 1928 году и Гамбелем в 1958 году.

Характеристики

Один параметр Фреше с параметром $\alpha$ имеет стандартизированный момент

$\mu _{k}=\int _{0}^{\infty }x^{k}f(x)dx=\int _{0}^{\infty }t^{-{\frac {k}{\alpha }}}e^{-t}\,dt,$

(с $t=x^{-\alpha }$) определено только для $k<\alpha$:

$\mu _{k}=\Gamma \left(1-{\frac {k}{\alpha }}\right)$

где $\Gamma \left(z\right)$ это гамма-функция .

В частности:

• Для $\alpha >1$ ожидание ​ ​ $E[X]=\Gamma (1-{\tfrac {1}{\alpha }})$
• Для $\alpha >2$ дисперсия ​ ​ ${\text{Var}}(X)=\Gamma (1-{\tfrac {2}{\alpha }})-{\big (}\Gamma (1-{\tfrac {1}{\alpha }}){\big )}^{2}.$

Квантиль ​ $q_{y}$ порядка $y$ может быть выражено через обратное распределение,

$q_{y}=F^{-1}(y)=\left(-\log _{e}y\right)^{-{\frac {1}{\alpha }}}$.

В частности, медиана равна:

$q_{1/2}=(\log _{e}2)^{-{\frac {1}{\alpha }}}.$

Способ : распространения $\left({\frac {\alpha }{\alpha +1}}\right)^{\frac {1}{\alpha }}.$

Специально для трехпараметрического метода Фреше первый квартиль равен $q_{1}=m+{\frac {s}{\sqrt[{\alpha }]{\log(4)}}}$ и третий квартиль $q_{3}=m+{\frac {s}{\sqrt[{\alpha }]{\log({\frac {4}{3}})}}}.$

Также квантилями для среднего и моды являются:

$F(mean)=\exp \left(-\Gamma ^{-\alpha }\left(1-{\frac {1}{\alpha }}\right)\right)$

$F(mode)=\exp \left(-{\frac {\alpha +1}{\alpha }}\right).$

Приложения

Подобрано кумулятивное распределение Фреше для экстремальных однодневных осадков.

• В гидрологии распределение Фреше применяется к экстремальным явлениям, таким как годовое максимальное количество осадков за один день и речной сток. Синее изображение, сделанное с помощью CumFreq , иллюстрирует пример аппроксимации распределения Фреше для ранжированного ежегодного максимального количества осадков за один день в Омане, демонстрируя также 90% доверительный интервал, основанный на биномиальном распределении . Совокупная частота данных об осадках представлена ​​в виде позиций на графике в рамках анализа совокупной частоты .

Однако в большинстве гидрологических приложений аппроксимация распределения осуществляется с помощью обобщенного распределения экстремальных значений , поскольку это позволяет избежать предположения о том, что распределение не имеет нижней границы (как того требует распределение Фреше).

Анализ кривой падения. Модель Дуонга можно рассматривать как обобщение распределения Фреше.

• При анализе кривой падения динамика снижения темпов добычи нефти или газа из скважины с течением времени может быть описана распределением Фреше.
• Один тест для оценки того, является ли многомерное распределение асимптотически зависимым или независимым, состоит в преобразовании данных в стандартные поля Фреше с использованием преобразования $Z_{i}=-1/\log F_{i}(X_{i})$ а затем отображение декартовых координат в псевдополярные. $(R,W)=(Z_{1}+Z_{2},Z_{1}/(Z_{1}+Z_{2}))$. Ценности $R\gg 1$ соответствуют крайним данным, для которых хотя бы одна компонента велика, а $W$ приблизительно 1 или 0 соответствует только одному компоненту, являющемуся крайним.
• В экономике он используется для моделирования индивидуального компонента предпочтений людей в отношении различных продуктов ( Промышленная организация ), мест ( Городская экономика ) или фирм ( Экономика труда ).

Связанные дистрибутивы

• Если $X\sim U(0,1)\,$ ( Равномерное распределение (непрерывное) ), то $m+s(-\log(X))^{-1/\alpha }\sim {\textrm {Frechet}}(\alpha ,s,m)\,$
• Если $X\sim {\textrm {Frechet}}(\alpha ,s,m)\,$ затем $kX+b\sim {\textrm {Frechet}}(\alpha ,ks,km+b)\,$
• Если $X_{i}\sim {\textrm {Frechet}}(\alpha ,s,m)\,$ и $Y=\max\{\,X_{1},\ldots ,X_{n}\,\}\,$ затем $Y\sim {\textrm {Frechet}}(\alpha ,n^{\tfrac {1}{\alpha }}s,m)\,$
• Кумулятивная функция распределения распределения Фреше решает постулата максимальной устойчивости уравнение
• Если $X\sim {\textrm {Frechet}}(\alpha ,s,m=0)\,$ тогда его обратная величина распределена по Вейбуллу : $X^{-1}\sim {\textrm {Weibull}}(k=\alpha ,\lambda =s^{-1})\,$

Характеристики

• Распределение Фреше является максимально стабильным распределением.
• Отрицательная величина случайной величины, имеющей распределение Фреше, представляет собой минимальное стабильное распределение.

См. также

• Распространение гумбеля типа 2
• Теорема Фишера – Типпетта – Гнеденко.

Дальнейшее чтение

• Коц, С.; Надараджа, С. (2000). Распределения экстремальных значений: теория и приложения . Всемирная научная. ISBN  1-86094-224-5 .

Внешние ссылки

• Хурайра, Ахмед; Ибрагим, Нур Акма; сын Давида Иса; Харон, Кассим (февраль 2005 г.). «Применение нового распределения экстремальных значений к данным о загрязнении воздуха». Управление качеством окружающей среды . 16 (1): 17–25. дои : 10.1108/14777830510574317 . ISSN   1477-7835 .
• «wfrechstat: среднее значение и дисперсия распределения Фреше» . Волновой анализ усталости и океанографии (WAFO) ( программное обеспечение и документация Matlab ). Центр математической науки. Лундский университет / Лундский технологический институт . Проверено 11 ноября 2023 г. - через www.maths.lth.se.