Доверительный интервал

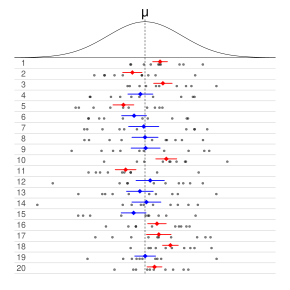
Неформально, в частотной статистике ( доверительный интервал CI ) — это интервал, который, как ожидается, обычно содержит параметр оцениваемый . Точнее, с учетом уровня доверия $\gamma$ (95% и 99% — типичные значения), ДИ — это случайный интервал, содержащий оцениваемый параметр. $\gamma$ % времени. ^[1]^[2] Уровень уверенности , степень уверенности или коэффициент уверенности представляет собой долгосрочную долю ДИ (при данном уровне достоверности), которые теоретически содержат истинное значение параметра; это эквивалентно номинальной вероятности покрытия . Например, из всех интервалов, рассчитанных на уровне 95 %, 95 % должны содержать истинное значение параметра. ^[3]

Факторы, влияющие на ширину ДИ, включают размер выборки , изменчивость выборки и уровень достоверности. ^[4] При прочих равных условиях более крупная выборка дает более узкий доверительный интервал, большая вариабельность выборки дает более широкий доверительный интервал, а более высокий уровень достоверности дает более широкий доверительный интервал. ^[5]

Определение

Позволять $X$ быть случайной выборкой из распределения вероятностей со статистическим параметром $\theta$ , которое представляет собой величину, которую необходимо оценить, и $\varphi$ , представляющий величины, которые не представляют непосредственного интереса. Доверительный интервал для параметра $\theta$ , с уровнем достоверности или коэффициентом $\gamma$ , представляет собой интервал $(u(X),v(X))$ определяется случайными величинами $u(X)$ и $v(X)$ с имуществом:

P(u(X)<\theta <v(X))=\gamma \quad {\text{ for every }}(\theta ,\varphi ).

Число $\gamma$ , типичное значение которого близко, но не превышает 1, иногда выражается в виде $1-\alpha$ (или в процентах $100\%\cdot (1-\alpha )$ ), где $\alpha$ — небольшое положительное число, часто 0,05.

Это важно для границ $u(X)$ и $v(X)$ указываться таким образом, чтобы до тех пор, пока $X$ собирается случайным образом, каждый раз, когда мы вычисляем доверительный интервал, существует вероятность $\gamma$ что оно будет содержать $\theta$ , истинное значение оцениваемого параметра. Это должно справедливо для любого фактического $\theta$ и $\varphi$ . ^[2]

Приблизительные доверительные интервалы

Во многих приложениях трудно построить доверительные интервалы, которые имеют точно необходимый уровень доверия, но приблизительные интервалы можно вычислить. Правило построения интервала можно принять как обеспечивающее доверительный интервал на уровне $\gamma$ если

P(u(X)<\theta <v(X))\approx \ \gamma \quad {\text{ for every }}(\theta ,\varphi )

до приемлемого уровня приближения. Альтернативно, некоторые авторы ^[6] просто требуйте этого

P(u(X)<\theta <v(X))\geq \ \gamma \quad {\text{ for every }}(\theta ,\varphi ),

что полезно, если вероятности идентифицированы лишь частично или неточно , а также при работе с дискретными распределениями . Доверительные пределы формы

P(u(X)<\theta )\geq \ \gamma

и

P(\theta <v(X))\geq \gamma

называются консервативными ; ^[7]^{(стр. 210)} соответственно, говорят о консервативных доверительных интервалах и вообще о регионах.

Желаемые свойства

При применении стандартных статистических процедур часто используются стандартные способы построения доверительных интервалов. Они будут разработаны таким образом, чтобы обеспечить определенные желательные свойства, которые будут сохраняться при условии, что предположения, на которых основана процедура, верны. Эти желательные свойства можно описать как: достоверность, оптимальность и инвариантность.

Из этих трех наиболее важным является «действительность», за которым следует «оптимальность». «Инвариантность» можно рассматривать как свойство метода получения доверительного интервала, а не правила построения интервала. В нестандартных приложениях следует искать те же желательные свойства:

Срок действия

Это означает, что номинальная вероятность покрытия (уровень доверия) доверительного интервала должна соблюдаться либо точно, либо с хорошим приближением.

Оптимальность

Это означает, что правило построения доверительного интервала должно максимально использовать информацию из набора данных.

Одним из способов оценки оптимальности является ширина интервала, так что правило построения доверительного интервала оценивается лучше, чем другое, если оно приводит к интервалам, ширина которых обычно короче.

Инвариантность

Во многих приложениях оцениваемое количество не может быть четко определено как таковое.

Например, опрос может привести к оценке медианного дохода населения, но его в равной степени можно рассматривать и как оценку логарифма медианного дохода, учитывая, что это обычная шкала для представления графических результатов. Было бы желательно, чтобы метод, используемый для построения доверительного интервала для медианного дохода, давал эквивалентные результаты при применении к построению доверительного интервала для логарифма медианного дохода: в частности, значения на концах последнего интервала были бы логарифмами. значений на концах бывшего интервала.

Методы вывода

Для нестандартных приложений существует несколько путей, по которым можно вывести правило построения доверительных интервалов. Установленные правила для стандартных процедур могут быть оправданы или объяснены несколькими из этих путей. Обычно правило построения доверительных интервалов тесно связано с конкретным способом нахождения точечной оценки рассматриваемой величины.

Сводная статистика

Это тесно связано с методом моментов оценки. Возникает простой пример, когда оцениваемой величиной является среднее значение генеральной совокупности, и в этом случае естественной оценкой является выборочное среднее значение. Аналогично, выборочную дисперсию можно использовать для оценки генеральной дисперсии. Доверительный интервал для истинного среднего значения может быть построен по центру выборочного среднего значения с шириной, кратной квадратному корню выборочной дисперсии.

Теория правдоподобия

Оценки могут быть построены с использованием принципа максимального правдоподобия , теория правдоподобия для этого предусматривает два способа построения доверительных интервалов или доверительных областей для оценок.

Оценочные уравнения

Оценочный подход здесь можно рассматривать как обобщение метода моментов и обобщение подхода максимального правдоподобия. Существуют соответствующие обобщения результатов теории максимального правдоподобия, которые позволяют строить доверительные интервалы на основе оценок, полученных из оценочных уравнений . ^{[ нужна ссылка ]}

Проверка гипотез

Если для общих значений параметра доступны тесты гипотез, то доверительные интервалы/области могут быть построены путем включения в доверительную область 100 $p$ % всех тех точек, для которых проверка нулевой гипотезы о том, что истинное значение является заданным значением, является не отвергается на уровне значимости (1 - $p$ ). ^[7]^{(п. 7.2 (iii))}

Начальная загрузка

В ситуациях, когда предположения о распределении для вышеупомянутых методов неопределенны или нарушаются, методы повторной выборки позволяют построить доверительные интервалы или интервалы прогнозирования. Наблюдаемое распределение данных и внутренние корреляции используются в качестве замены корреляций в более широкой популяции.

Центральная предельная теорема

Центральная предельная теорема является уточнением закона больших чисел . Для большого числа независимых одинаково распределенных случайных величин $X_{1},...,X_{n},$ с конечной дисперсией, среднее ${\overline {X}}_{n}$ приблизительно имеет нормальное распределение, независимо от распределения $X_{i}$ то есть приближение примерно улучшается пропорционально ${\sqrt {n}}$ . ^[2]

Пример

На этой гистограмме верхние концы коричневых столбцов обозначают наблюдаемые средние значения, а сегменты красных линий (« столбики ошибок ») представляют доверительные интервалы вокруг них. Хотя полосы погрешностей показаны симметрично относительно средних значений, это не всегда так. На большинстве графиков полосы ошибок не представляют доверительные интервалы (например, они часто представляют стандартные ошибки или стандартные отклонения).

Предполагать ${X_{1},\ldots ,X_{n}}$ представляет собой независимую выборку из нормально распределенной совокупности с неизвестными параметрами . $\mu$ и дисперсия $\sigma ^{2}.$ Позволять

{\bar {X}}={\frac {X_{1}+\cdots +X_{n}}{n}},

S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}.

Где ${\bar {X}}$ — выборочное среднее , и $S^{2}$ – это выборочная дисперсия . Затем

T={\frac {{\bar {X}}-\mu }{S/{\sqrt {n}}}}

имеет Стьюдента распределение с $n-1$ степени свободы. ^[8] Обратите внимание, что распределение $T$ не зависит от значений ненаблюдаемых параметров $\mu$ и $\sigma ^{2}$ ; т. е. это ключевая величина . Предположим, мы хотим рассчитать 95% доверительный интервал для $\mu .$ Тогда, обозначив $c$ как 97,5-й процентиль этого распределения,

P_{T}(-c\leq T\leq c)=0.95.

Обратите внимание, что «97,5» и «0,95» являются правильными в предыдущих выражениях. Вероятность того, что это произойдет, составляет 2,5%. $T$ будет меньше, чем $-c$ и вероятность 2,5%, что оно будет больше, чем $+c.$ Таким образом, вероятность того, что $T$ будет между $-c$ и $+c$ составляет 95%. $P_{T}$ это вероятностная мера под студентом $t$ распределение.

Следовательно,

P_{\mu }\left({\bar {X}}-{\frac {cS}{\sqrt {n}}}\leq \mu \leq {\bar {X}}+{\frac {cS}{\sqrt {n}}}\right)=0.95,

и у нас есть теоретический (стохастический) 95% доверительный интервал для $\mu .$ Здесь $P_{\mu }$ — вероятностная мера при неизвестном распределении $\mu$ .

После наблюдения за образцом находим значения ${\bar {x}}$ для ${\bar {X}}$ и $s$ для $S,$ из которого мы вычисляем доверительный интервал

\left[{\bar {x}}-{\frac {cs}{\sqrt {n}}},{\bar {x}}+{\frac {cs}{\sqrt {n}}}\right].

Интерпретация

Могут быть даны различные интерпретации доверительного интервала (в качестве примера ниже взят 95% доверительный интервал).

Доверительный интервал может быть выражен через долгосрочную частоту повторных выборок (или повторной выборки ): параметр будет стремиться к 95%». ^[9]
Доверительный интервал можно выразить через вероятность относительно одной теоретической (еще не реализованной) выборки: «Существует 95%-ная вероятность того, что 95%-ный доверительный интервал, рассчитанный на основе данной будущей выборки, будет охватывать истинное значение параметр населения». [10] По сути, это переосмысливает интерпретацию «повторяющихся выборок» как вероятность, а не как частоту.
Доверительный интервал может быть выражен через статистическую значимость, например: «95% доверительный интервал представляет собой значения, которые статистически значимо не отличаются от точечной оценки на уровне 0,05». ^[11]

Распространенные недоразумения

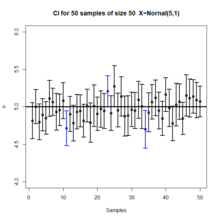
Доверительные интервалы и уровни часто неправильно понимаются, а опубликованные исследования показали, что даже профессиональные ученые часто неправильно их интерпретируют. ^[12]^[13]^[14]^[15]^[16]^[17]

Уровень достоверности 95 % не означает, что для данного реализованного интервала существует 95 % вероятность того, что параметр совокупности находится внутри интервала (т. е. 95 % вероятность того, что интервал покрывает параметр совокупности). ^[18] Согласно частотной интерпретации, после расчета интервала этот интервал либо покрывает значение параметра, либо нет; это уже не вопрос вероятности. Вероятность 95% относится к надежности процедуры оценки, а не к конкретному расчетному интервалу. ^[19] Сам Нейман (первоначальный сторонник доверительных интервалов) высказал это мнение в своей оригинальной статье: ^[10]
Следует отметить, что в приведенном выше описании утверждения о вероятности относятся к проблемам оценки, которыми статистика будет заниматься в будущем. На самом деле, я неоднократно заявлял, что частота правильных результатов будет стремиться к α . Рассмотрим теперь случай, когда выборка уже взята и расчеты дали [частные пределы]. Можем ли мы сказать, что в данном конкретном случае вероятность истинного значения [попадания между этими пределами] равна α ? Ответ, очевидно, отрицательный. Параметр представляет собой неизвестную константу, и относительно его значения нельзя сделать никаких утверждений о вероятности...

Уровень достоверности 95 % не означает, что 95 % данных выборки находятся в пределах доверительного интервала.
Уровень достоверности 95% не означает, что существует 95% вероятность того, что оценка параметра при повторении эксперимента попадет в доверительный интервал, рассчитанный на основе данного эксперимента. ^[16]

Примеры того, насколько наивная интерпретация доверительных интервалов может быть проблематичной

Доверительная процедура для единообразного местоположения

Уэлч ^[20] интервалы Фишера представил пример, который ясно показывает разницу между теорией доверительных интервалов и другими теориями интервальной оценки (включая доверительные и объективные байесовские интервалы). Робинсон ^[21] назвал этот пример «[p] возможно, самым известным контрпримером для версии теории доверительных интервалов Неймана». Для Уэлча это показало превосходство теории доверительных интервалов; критикам теории она показывает недостаток. Здесь мы представляем упрощенную версию.

Предположим, что $X_{1},X_{2}$ являются независимыми наблюдениями из однородного $(\theta -1/2,\theta +1/2)$ распределение. Тогда оптимальная процедура доверительности 50% для $\theta$ является ^[22]

{\bar {X}}\pm {\begin{cases}{\dfrac {|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|<1/2\\[8pt]{\dfrac {1-|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|\geq 1/2.\end{cases}}

Для получения интервальной оценки можно использовать фидуциальный или объективный байесовский аргумент.

{\bar {X}}\pm {\frac {1-|X_{1}-X_{2}|}{4}},

что также является процедурой доверия 50%. Уэлч показал, что первая доверительная процедура доминирует над второй, согласно требованиям теории доверительных интервалов; для каждого $\theta _{1}\neq \theta$ , вероятность того, что первая процедура содержит $\theta _{1}$ меньше или равно вероятности того, что вторая процедура содержит $\theta _{1}$ . Средняя ширина интервалов у первой процедуры меньше, чем у второй. Следовательно, первая процедура предпочтительна в рамках классической теории доверительного интервала.

Однако, когда $|X_{1}-X_{2}|\geq 1/2$ , интервалы из первой процедуры гарантированно содержат истинное значение $\theta$ : Следовательно, номинальный коэффициент достоверности 50% не связан с неопределенностью, которую мы должны иметь в отношении того, что определенный интервал содержит истинное значение. Вторая процедура этим свойством не обладает.

Более того, когда первая процедура генерирует очень короткий интервал, это указывает на то, что $X_{1},X_{2}$ расположены очень близко друг к другу и, следовательно, предоставляют информацию только в одной точке данных. Однако первый интервал из-за своей малой ширины исключит почти все разумные значения параметра. Вторая процедура этим свойством не обладает.

Два противоречивых свойства первой процедуры – 100% охват при $X_{1},X_{2}$ находятся далеко друг от друга и охват почти 0%, когда $X_{1},X_{2}$ расположены близко друг к другу – сбалансируйте их, чтобы обеспечить охват в среднем 50%. Однако, несмотря на то, что первая процедура является оптимальной, ее интервалы не дают ни оценки точности оценки, ни оценки неопределенности, которую следует иметь в отношении того, что интервал содержит истинное значение.

Этот пример используется для аргументации против наивных интерпретаций доверительных интервалов. Если утверждается, что доверительная процедура имеет свойства, выходящие за рамки номинального покрытия (например, отношение к точности или связь с байесовским выводом), эти свойства должны быть доказаны; они не следуют из того факта, что процедура является доверительной процедурой.

Доверительная процедура для ω ²

Штайгер ^[23] предложил ряд доверительных процедур для общих показателей величины эффекта в ANOVA . Мори и др. ^[18] отметим, что некоторые из этих доверительных процедур, включая процедуру для ω ², обладают тем свойством, что по мере того, как статистика F становится все более маленькой, что указывает на несоответствие всем возможным значениям ω ²— доверительный интервал сужается и может даже содержать только одно значение ω ² = 0; то есть КИ бесконечно узок (это происходит, когда $p\geq 1-\alpha /2$ для $100(1-\alpha )\%$ ТАМ).

Такое поведение согласуется с взаимосвязью между доверительной процедурой и проверкой значимости : поскольку F становится настолько малым, что групповые средние оказываются гораздо ближе друг к другу, чем мы могли бы случайно ожидать, проверка значимости может указывать на отклонение большинства или всех значений ω. ². Следовательно, интервал будет очень узким или даже пустым (или, по соглашению, предложенному Штайгером, содержащим только 0). Однако это не означает, что оценка ω ² очень точен. В каком-то смысле это указывает на обратное: достоверность самих результатов может оказаться под вопросом. Это противоречит общепринятой интерпретации доверительных интервалов, согласно которой они отражают точность оценки.

История

Методы расчета доверительных интервалов для биномиальной пропорции появились с 1920-х годов. ^[24]^[25] Основные идеи доверительных интервалов в целом были разработаны в начале 1930-х гг. ^[26]^[27]^[28] а первый подробный и общий отчет был сделан Ежи Нейманом в 1937 году. ^[10]

Нейман описал развитие идей следующим образом (номера ссылок изменены): ^[28]

[Моя работа над доверительными интервалами] возникла примерно в 1930 году из простого вопроса Вацлава Пытковского, тогда моего студента в Варшаве, который занимался эмпирическим исследованием экономики сельского хозяйства. Вопрос заключался в следующем: как недогматично охарактеризовать точность оценки коэффициента регрессии? ...
Монография Питковского... появилась в печати в 1932 году. ^[29] Так случилось, что несколько раньше Фишер опубликовал свою первую статью. ^[30] занимается фидуциальным распределением и фидуциальным аргументом. Совершенно неожиданно, хотя концептуальная основа фидуциального аргумента полностью отличается от концептуальной основы доверительных интервалов, конкретные решения нескольких частных проблем совпали. Так, в первой статье, в которой я представил теорию доверительных интервалов, опубликованной в 1934 г., ^[26] Я признал приоритет Фишера в идее о том, что интервальная оценка возможна без какой-либо ссылки на теорему Байеса и с априорной независимостью решения от вероятностей . В то же время я мягко предположил, что подход Фишера к проблеме заключался в небольшом недоразумении.

В медицинских журналах доверительные интервалы стали пропагандироваться в 1970-х годах, но стали широко использоваться только в 1980-х. ^[31] К 1988 году медицинские журналы потребовали сообщать доверительные интервалы. ^[32]

См. также

Верхние пределы CL (физика элементарных частиц)
Правило 68–95–99,7
Доверительный диапазон , интервальная оценка кривой
Распределение уверенности
Доверительная область , обобщение более высокого измерения.
Доверие (статистика) – мера силы убеждения, используемая в статистике.
Достоверный интервал , байесовская альтернатива интервальной оценке.
Непараметрический доверительный интервал на основе кумулятивной функции распределения
Панель ошибок – графическое представление изменчивости данных.
Статистика оценок - подход к анализу данных в частотной статистике
Погрешность , полуширина CI
p-значение - функция наблюдаемых результатов выборки.
Интервал прогнозирования , интервальная оценка случайной величины.
Возможная ошибка
Надежные доверительные интервалы — статистические показатели отклонения выборки.