Статистика оценки
Статистика оценки , или просто оценка , представляет собой структуру анализа данных, которая использует комбинацию размеров эффекта , доверительных интервалов , точного планирования и метаанализа для планирования экспериментов, анализа данных и интерпретации результатов. [1] Он дополняет подходы к проверке гипотез, такие как проверка значимости нулевой гипотезы (NHST), выходя за рамки вопроса о наличии или отсутствии эффекта, и предоставляет информацию о том, насколько велик эффект. [2] [3] Оценочную статистику иногда называют новой статистикой . [3] [4] [5]
Основная цель методов оценки — сообщить о величине эффекта ( точечной оценке ) вместе с доверительным интервалом , последний из которых связан с точностью оценки. [6] Доверительный интервал суммирует диапазон вероятных значений основного популяционного эффекта. Сторонники оценки рассматривают сообщение о P значении как бесполезное отвлечение от важного дела, связанного с сообщением о величине эффекта с его доверительными интервалами. [7] и считают, что оценка должна заменить проверку значимости для анализа данных. [8] [9]
История
[ редактировать ]Начиная с 1929 года физик Раймонд Тайер Бирдж публиковал обзорные статьи. [10] в котором он использовал методы средневзвешенных значений для расчета оценок физических констант - процедуру, которую можно рассматривать как предшественник современного метаанализа . [11]
В 1930-х годах Ежи Нейман опубликовал серию статей по статистическому оцениванию, в которых определил математику и терминологию доверительных интервалов . [12] [13] [14]
В 1960-х годах оценочная статистика была принята нефизическими науками с разработкой стандартизированной величины эффекта Джейкобом Коэном .
В 1970-х годах синтез современных исследований был впервые осуществлен Джином В. Глассом, опубликовавшим первый систематический обзор и метаанализ психотерапии. [15] Эта новаторская работа впоследствии повлияла на внедрение метаанализа для лечения в целом.
В 1980-х и 1990-х годах методы оценки были расширены и усовершенствованы для практического применения специалистами по биостатистике, включая Ларри Хеджеса , Майкла Боренштейна, Дуга Альтмана , Мартина Гарднера и многих других, с развитием современного (медицинского) метаанализа .
Начиная с 1980-х годов систематический обзор , используемый в сочетании с метаанализом, стал методом, широко используемым в медицинских исследованиях. имеется более 200 000 ссылок на «метаанализ» В PubMed .
В 1990-х годах редактор Кеннет Ротман запретил использование p-значений в журнале «Эпидемиология» ; согласие было высоким среди авторов, но это существенно не изменило их аналитическое мышление. [16]
В 2010-х годах Джефф Камминг опубликовал учебник, посвященный статистике оценок, а также программное обеспечение в Excel, предназначенное для обучения мышлению о величине эффекта, в первую очередь психологов. [17] Также в 2010-х годах методы оценки получили все большее распространение в нейробиологии. [18] [19]
В 2013 году Руководство для публикаций Американской психологической ассоциации рекомендовало использовать оценку в дополнение к проверке гипотез. [20] Также в 2013 году в документе «Единые требования к рукописям, представляемым в биомедицинские журналы» содержалась аналогичная рекомендация: «Избегайте полагаться исключительно на проверку статистических гипотез, таких как значения P, которые не могут передать важную информацию о величине эффекта». [21]
В 2019 году более 800 ученых подписали открытый комментарий, призывающий отказаться от всей концепции статистической значимости. [22]
В 2019 году Общества нейронаук журнал eNeuro ввел политику, рекомендующую использование оценочных графиков в качестве предпочтительного метода представления данных. [23] А в 2022 году редакторы журналов Международного общества физиотерапии рекомендовали использовать методы оценки вместо статистических тестов с нулевой гипотезой. [24]
Несмотря на широкое внедрение метаанализа в клинических исследованиях и рекомендации нескольких крупных издательских учреждений, система оценки обычно не используется в первичных биомедицинских исследованиях. [25]
Методология
[ редактировать ]Многие тесты значимости имеют оценочный аналог; [26] почти в каждом случае результат теста (или его значение p ) можно просто заменить величиной эффекта и оценкой точности. Например, вместо использования t-критерия Стьюдента аналитик может сравнить две независимые группы, рассчитав среднюю разницу и ее 95% доверительный интервал . Соответствующие методы можно использовать для парного t-теста и множественных сравнений. Аналогично, для регрессионного анализа аналитик сообщит коэффициент детерминации (R 2 ) и уравнение модели вместо p-значения модели.
Однако сторонники оценочной статистики предостерегают от сообщения лишь нескольких цифр. Вместо этого рекомендуется анализировать и представлять данные с помощью визуализации данных. [2] [5] [6] Примеры подходящих визуализаций включают диаграмму рассеяния для регрессии и графики Гарднера-Альтмана для двух независимых групп. [27] Хотя графики групп исторических данных (столбчатые диаграммы, коробчатые диаграммы и графики скрипки) не отображают сравнение, оценочные графики добавляют вторую ось для явной визуализации размера эффекта. [28]
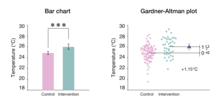
График Гарднера-Альтмана
[ редактировать ]График разницы средних Гарднера-Альтмана был впервые описан Мартином Гарднером и Дугом Альтманом в 1986 году; [27] это статистический график, предназначенный для отображения данных двух независимых групп. [5] Существует также версия, подходящая для парных данных . Ключевые инструкции по созданию этой диаграммы заключаются в следующем: (1) отобразите все наблюдаемые значения для обеих групп рядом друг с другом; (2) поместите вторую ось справа, сместив ее, чтобы показать шкалу средней разницы; и (3) постройте среднюю разницу с ее доверительным интервалом в виде маркера с полосами ошибок. [3] Графики Гарднера-Альтмана можно создать с помощью DABEST-Python или dabestr ; в качестве альтернативы аналитик может использовать программное обеспечение с графическим интерфейсом, например приложение Estimation Stats .

Заговор Камминга
[ редактировать ]Для нескольких групп Джефф Камминг предложил использовать вторичную панель для построения двух или более средних различий и их доверительных интервалов, расположенную под панелью наблюдаемых значений; [3] такое расположение позволяет легко сравнивать средние различия («дельты») по нескольким группам данных. Графики Камминга можно создавать с помощью пакета ESCI , DABEST или приложения Estimation Stats .
Другие методологии
[ редактировать ]Помимо средней разницы, существует множество других типов величины эффекта , каждый из которых имеет относительные преимущества. Основные типы включают величину эффекта в классе стандартизированных показателей Коэна d и коэффициент детерминации (R 2 ) для регрессионного анализа . Для ненормальных распределений существует ряд более надежных величин эффекта , включая дельту Клиффа и статистику Колмогорова-Смирнова .
Ошибки в проверке гипотез
[ редактировать ]При проверке гипотез основной целью статистических вычислений является получение значения p , вероятности увидеть полученный результат или более экстремальный результат, если предположить, что нулевая гипотеза верна. Если значение p низкое (обычно <0,05), специалисту по статистике рекомендуется отвергнуть нулевую гипотезу. Сторонники оценки отвергают достоверность проверки гипотез. [3] [6] по следующим причинам, среди прочего:
- P-значения легко и часто неправильно интерпретируются. Например, значение p часто ошибочно принимают за «вероятность того, что нулевая гипотеза верна».
- Нулевая гипотеза всегда неверна для любого набора наблюдений: всегда есть какой-то эффект, даже если он незначительный. [29]
- Проверка гипотез дает дихотомические ответы «да-нет», отбрасывая при этом важную информацию о величине. [30]
- Любое конкретное значение p возникает в результате взаимодействия размера эффекта , размера выборки (при прочих равных условиях больший размер выборки дает меньшее значение p) и ошибки выборки. [31]
- При малой мощности моделирование показывает, что ошибка выборки делает значения p чрезвычайно нестабильными. [32]
Преимущества оценочной статистики
[ редактировать ]Количественная оценка
[ редактировать ]В то время как значения p фокусируются на ответах «да» или «нет», оценка направляет внимание аналитика на количественную оценку.
Преимущества доверительных интервалов
[ редактировать ]Доверительные интервалы ведут себя предсказуемым образом. По определению, 95% доверительные интервалы имеют 95% вероятность охвата основного генерального среднего значения (μ). Эта особенность остается постоянной при увеличении размера выборки; меняется то, что интервал становится меньше. Кроме того, 95% доверительные интервалы также являются 83% интервалами прогнозирования: один (доэкспериментальный) доверительный интервал имеет 83% вероятность охватить среднее значение любого будущего эксперимента. [3] Таким образом, знание 95% доверительных интервалов одного эксперимента дает аналитику разумный диапазон среднего значения генеральной совокупности. Тем не менее, доверительные распределения и апостериорные распределения предоставляют гораздо больше информации, чем одноточечная оценка или интервалы. [33] это может усугубить дихотомическое мышление в зависимости от интервала, охватывающего или не охватывающего «нулевое» интересующее значение (т. е. индуктивное поведение Неймана в отличие от поведения Фишера). [34] ).
Доказательная статистика
[ редактировать ]Психологические исследования восприятия статистики показывают, что интервальные оценки отчетности обеспечивают более точное восприятие данных, чем отчетные p-значения. [35]
Точное планирование
[ редактировать ]Точность оценки формально определяется как 1/ дисперсия и, как и степень, увеличивается (улучшается) с увеличением размера выборки. Как и мощность , высокий уровень точности стоит дорого; Заявки на исследовательские гранты в идеале должны включать анализ точности/затрат. Сторонники оценки считают, что точное планирование должно заменить власть , поскольку сама статистическая мощность концептуально связана с проверкой значимости. [3] Точное планирование можно выполнить с помощью веб-приложения ESCI .
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Эллис, Пол. «Часто задаваемые вопросы о размере эффекта» .
- ^ Перейти обратно: а б Коэн, Джейкоб. «Земля круглая (p<0,05)» (PDF) . Архивировано из оригинала (PDF) 11 октября 2017 г. Проверено 22 августа 2013 г.
- ^ Перейти обратно: а б с д и ж г Камминг, Джефф (2011). Понимание новой статистики: размеры эффекта, доверительные интервалы и метаанализ . Нью-Йорк: Рутледж. ISBN 978-0415879675 . [ нужна страница ]
- ^ Альтман, Дуглас (1991). Практическая статистика медицинских исследований . Лондон: Чепмен и Холл.
- ^ Перейти обратно: а б с Дуглас Альтман, изд. (2000). Статистика с уверенностью . Лондон: Уайли-Блэквелл. [ нужна страница ]
- ^ Перейти обратно: а б с Коэн, Джейкоб (1990). «Вещи, которые я узнал (на данный момент)» . Американский психолог . 45 (12): 1304–1312. дои : 10.1037/0003-066x.45.12.1304 .
- ^ Эллис, Пол (31 мая 2010 г.). «Почему я не могу просто судить о своем результате, глядя на значение p?» . Проверено 5 июня 2013 г.
- ^ Кларидж-Чанг, Адам; Ассам, Присели Н. (2016). «Оценочная статистика должна заменить тестирование значимости» . Природные методы . 13 (2): 108–109. дои : 10.1038/nmeth.3729 . ПМИД 26820542 . S2CID 205424566 .
- ^ Бернер, Дэниел; Амрайн, Валентин (2022). «Почему и как нам следует присоединиться к переходу от тестирования значимости к оценке» . Журнал эволюционной биологии . 35 (6): 777–787. дои : 10.1111/jeb.14009 . ISSN 1010-061X . ПМЦ 9322409 . ПМИД 35582935 . S2CID 247788899 .
- ^ Бирдж, Раймонд Т. (1929). «Вероятные значения общих физических констант». Обзоры современной физики . 1 (1): 1–73. Бибкод : 1929РвМП....1....1Б . дои : 10.1103/RevModPhys.1.1 .
- ^ Хеджес, Ларри (1987). «Насколько сложна точная наука и насколько мягка мягкая наука». Американский психолог . 42 (5): 443. CiteSeerX 10.1.1.408.2317 . дои : 10.1037/0003-066x.42.5.443 .
- ^ Нейман, Дж. (1934). О двух различных аспектах репрезентативного метода: методе стратифицированной выборки и методе целенаправленного отбора. Журнал Королевского статистического общества, 97 (4), 558–625. https://doi.org/10.2307/2342192 (см. примечание I в приложении)
- ^ Дж. Нейман (1935), Энн. Математика. Статист. 6 (3): 111–116 (сентябрь 1935 г.). https://doi.org/10.1214/aoms/1177732585
- ^ Нейман, Дж. (1937). «Очерк теории статистического оценивания, основанной на классической теории вероятностей». Философские труды Королевского общества А. 236 (767): 333–380. Бибкод:1937RSPTA.236..333N. doi:10.1098/rsta.1937.0005. JSTOR 91337.
- ^ Хант, Мортон (1997). Как наука подводит итоги: история метаанализа . Нью-Йорк: Фонд Рассела Сейджа. ISBN 978-0-87154-398-1 .
- ^ Фидлер, Фиона; Томасон, Нил; Камминг, Джефф; Финч, Сью; Лиман, Джоанна (2004). «Редакторы могут привести исследователей к доверительным интервалам, но не могут заставить их задуматься: уроки статистической реформы в медицине». Психологическая наука . 15 (2): 119–126. дои : 10.1111/j.0963-7214.2004.01502008.x . ПМИД 14738519 . S2CID 21199094 .
- ^ Камминг, Джефф. «ESCI (Исследовательское программное обеспечение для доверительных интервалов)» . Архивировано из оригинала 29 декабря 2013 г. Проверено 12 мая 2013 г.
- ^ Йылдызоглу, Тугче; Вайслогель, Ян-Марек; Мохаммед, Фархан; Чан, Эдвин С.-Ю.; Ассам, Присели Н.; Кларидж-Чанг, Адам (2015). «Оценка обработки информации в системе памяти: полезность метааналитических методов для генетики» . ПЛОС Генетика . 11 (12): e1005718. дои : 10.1371/journal.pgen.1005718 . ПМЦ 4672901 . ПМИД 26647168 .
- ^ Хентшке, Харальд; Майк К. Штюттген (2011). «Расчет показателей величины эффекта для наборов данных нейробиологии». Европейский журнал неврологии . 34 (12): 1887–1894. дои : 10.1111/j.1460-9568.2011.07902.x . ПМИД 22082031 . S2CID 12505606 .
- ^ «Руководство по публикации Американской психологической ассоциации, шестое издание» . Архивировано из оригинала 5 марта 2013 г.
- ^ «Единые требования к рукописям, представляемым в биомедицинские журналы» . Архивировано из оригинала 15 мая 2013 года.
- ^ Амрайн, Валентин; Гренландия, Сандер; МакШейн, Блейк (2019). «Ученые восстают против статистической значимости» , Nature 567, 305–307.
- ^ Бернар, Кристоф (2019). «Изменение того, как мы сообщаем, интерпретируем и обсуждаем наши результаты, чтобы восстановить доверие к нашим исследованиям» . эНейро . 6 (4). дои : 10.1523/ENEURO.0259-19.2019 . ПМК 6709206 . ПМИД 31453315 .
- ^ Элкинс, Марк; и др. (2022). «Статистический вывод посредством оценки: рекомендации редакторов журналов Международного общества физиотерапии» , Журнал физиотерапии, 68 (1), 1-4.
- ^ Хэлси, Льюис Г. (2019). «Царство р-значения закончилось: какие альтернативные методы анализа мы могли бы использовать, чтобы заполнить вакуум власти?» . Письма по биологии . 15 (5): 20190174. doi : 10.1098/rsbl.2019.0174 . ПМК 6548726 . ПМИД 31113309 .
- ^ Камминг, Джефф; Калин-Джагеман, Роберт (2016). Введение в новую статистику: оценка, открытая наука и не только . Рутледж. ISBN 978-1138825529 . [ нужна страница ]
- ^ Перейти обратно: а б Гарднер, MJ; Альтман, Д.Г. (1986). «Доверительные интервалы, а не значения P: оценка, а не проверка гипотез» . БМЖ . 292 (6522): 746–750. дои : 10.1136/bmj.292.6522.746 . ПМЦ 1339793 . ПМИД 3082422 .
- ^ Эй, Хосес! Тумкая, Тайфун; Арьял, Самир; Чхве, Хёнвон; Кларидж-Чанг, Адам (2018). «Выход за рамки значений P: ежедневный анализ данных с оценочными графиками» . дои : 10.1101/377978 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Коэн, Джейкоб (1994). «Земля круглая (p < 0,05)». Американский психолог . 49 (12): 997–1003. дои : 10.1037/0003-066X.49.12.997 .
- ^ Эллис, Пол (2010). Основное руководство по размерам эффекта: статистическая мощность, метаанализ и интерпретация результатов исследований . Кембридж: Издательство Кембриджского университета. [ нужна страница ]
- ^ Дентон Э. Моррисон, Рамон Э. Хенкель, изд. (2006). Споры о тесте значимости: читатель . Альдинская сделка. ISBN 978-0202308791 . [ нужна страница ]
- ^ Камминг, Джефф. «Танец значений р» . Ютуб .
- ^ Се, Мин-ге; Сингх, Кесар (2013). «Распределение достоверности, оценка частотного распределения параметра: обзор». Международный статистический обзор . 81 (1): 3–39. дои : 10.1111/insr.12000 . JSTOR 43298799 . S2CID 3242459 .
- ^ Халпин, Питер Ф.; Стам, Хендерикус Дж. (2006). «Индуктивный вывод или индуктивное поведение: Фишер и Нейман: подходы Пирсона к статистическому тестированию в психологических исследованиях (1940–1960)». Американский журнал психологии . 119 (4): 625–653. дои : 10.2307/20445367 . JSTOR 20445367 . ПМИД 17286092 .
- ^ Бейт-Маром, Руфь; Фидлер, Фиона Маргарет; Камминг, Джеффри Дэвид (2008). «Статистическое познание: на пути к научно обоснованной практике в статистике и статистическом образовании». Журнал статистических исследований в области образования . 7 (2): 20–39. CiteSeerX 10.1.1.154.7648 . дои : 10.52041/serj.v7i2.468 . S2CID 18902043 .