Частичная корреляция

В вероятностей и статистике теории частичная корреляция измеряет степень связи между двумя случайными величинами без учета влияния набора управляющих случайных величин. При определении числовой взаимосвязи между двумя интересующими переменными использование их коэффициента корреляции приведет к вводящим в заблуждение результатам , если существует другая искажающая переменная , численно связанная с обеими интересующими переменными. Этой вводящей в заблуждение информации можно избежать, контролируя искажающую переменную, что осуществляется путем вычисления частного коэффициента корреляции. Именно это и является причиной включения других правых переменных в множественную регрессию ; но хотя множественная регрессия дает несмещенные результаты для размера эффекта , она не дает численного значения меры силы связи между двумя интересующими переменными.

Например, учитывая экономические данные о потреблении, доходе и богатстве различных людей, рассмотрим взаимосвязь между потреблением и доходом. Если не учитывать богатство при расчете коэффициента корреляции между потреблением и доходом, результат может оказаться ошибочным, поскольку доход может быть численно связан с богатством, которое, в свою очередь, может быть численно связано с потреблением; измеренная корреляция между потреблением и доходом может фактически быть искажена этими другими корреляциями. Использование частичной корреляции позволяет избежать этой проблемы.

Как и коэффициент корреляции, частный коэффициент корреляции принимает значение в диапазоне от –1 до 1. Значение –1 передает идеальную отрицательную корреляцию, контролирующую некоторые переменные (т. е. точную линейную зависимость, при которой более высокие значения одной переменной связаны с более низкими ценностями другого); значение 1 соответствует идеальной положительной линейной зависимости, а значение 0 означает отсутствие линейной зависимости.

Частичная корреляция совпадает с условной корреляцией , если случайные величины совместно распределены как многомерное нормальное , другое эллиптическое , многомерное гипергеометрическое , многомерное отрицательное гипергеометрическое , многомерное распределение или распределение Дирихле , но не в целом иначе. ^[1]

Формальное определение [ править ]

Формально частичная корреляция между X и Y с учетом набора из n управляющих переменных Z = { Z ₁ , Z ₂ , ..., Z _n }, записанная ρ _{XY · Z} , представляет собой корреляцию между остатками e _X и e _Y результате линейной регрессии X Z с в и Y с Z соответственно. Частная корреляция первого порядка (т. е. при n = 1) представляет собой разность между корреляцией и произведением устранимых корреляций, деленную на произведение коэффициентов отчуждения устранимых корреляций. Коэффициент отчуждения и его связь с совместной дисперсией посредством корреляции доступны у Гилфорда (1973, стр. 344–345). ^[2]

Вычисление [ править ]

Использование линейной регрессии [ править ]

Простой способ вычислить выборочную частичную корреляцию для некоторых данных — решить две связанные задачи линейной регрессии и вычислить корреляцию между остатками. Пусть X и Y — случайные величины, принимающие действительные значения, и пусть n Z — - мерная векторная случайная величина. Пусть x _i , y _i и z _i обозначают i -е число $N$ iid- наблюдения из некоторого совместного распределения вероятностей по реальным случайным переменным X , Y и Z , при этом zi _{был увеличен на 1 ,} чтобы обеспечить постоянный член регрессии. Решение задачи линейной регрессии сводится к нахождению ( n +1)-мерных векторов коэффициентов регрессии. $\mathbf {w} _{X}^{*}$ и $\mathbf {w} _{Y}^{*}$ такой, что

\mathbf {w} _{X}^{*}=\arg \min _{\mathbf {w} }\left\{\sum _{i=1}^{N}(x_{i}-\langle \mathbf {w} ,\mathbf {z} _{i}\rangle )^{2}\right\}

\mathbf {w} _{Y}^{*}=\arg \min _{\mathbf {w} }\left\{\sum _{i=1}^{N}(y_{i}-\langle \mathbf {w} ,\mathbf {z} _{i}\rangle )^{2}\right\}

где $N$ количество наблюдений, а $\langle \mathbf {w} ,\mathbf {z} _{i}\rangle$ скалярное произведение векторов $\mathbf {w}$ и $\mathbf {z} _{i}$ .

Остатки тогда

e_{X,i}=x_{i}-\langle \mathbf {w} _{X}^{*},\mathbf {z} _{i}\rangle

e_{Y,i}=y_{i}-\langle \mathbf {w} _{Y}^{*},\mathbf {z} _{i}\rangle

и выборочная частичная корреляция затем определяется по обычной формуле выборочной корреляции , но между этими новыми производными значениями:

{\begin{aligned}{\hat {\rho }}_{XY\cdot \mathbf {Z} }&={\frac {N\sum _{i=1}^{N}e_{X,i}e_{Y,i}-\sum _{i=1}^{N}e_{X,i}\sum _{i=1}^{N}e_{Y,i}}{{\sqrt {N\sum _{i=1}^{N}e_{X,i}^{2}-\left(\sum _{i=1}^{N}e_{X,i}\right)^{2}}}~{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^{2}-\left(\sum _{i=1}^{N}e_{Y,i}\right)^{2}}}}}\\&={\frac {N\sum _{i=1}^{N}e_{X,i}e_{Y,i}}{{\sqrt {N\sum _{i=1}^{N}e_{X,i}^{2}}}~{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^{2}}}}}.\end{aligned}}

В первом выражении все три члена после знака минус равны 0, поскольку каждый из них содержит сумму остатков обычной регрессии наименьших квадратов .

Пример [ править ]

Рассмотрим следующие данные о трех переменных: X , Y и Z :

Х	И	С
2	1	0
4	2	0
15	3	1
20	4	1

Вычисление коэффициента корреляции Пирсона между переменными X и Y дает примерно 0,970, а вычисление частной корреляции между X и Y по формуле, приведенной выше, дает частичную корреляцию 0,919. Вычисления проводились с использованием R со следующим кодом.

> X <- c(2,4,15,20)
> Y <- c(1,2,3,4)
> Z <- c(0,0,1,1)
> mm1 <- lm(X~Z)
> res1 <- mm1$residuals
> mm2 <- lm(Y~Z)
> res2 <- mm2$residuals
> cor(res1,res2)
[1] 0.919145
> cor(X,Y)
[1] 0.9695016
> generalCorr::parcorMany(cbind(X,Y,Z))
                 
     nami namj partij   partji rijMrji  
[1,] "X"  "Y"  "0.8844" "1"    "-0.1156"
[2,] "X"  "Z"  "0.1581" "1"    "-0.8419"

Нижняя часть приведенного выше кода сообщает, что обобщенный нелинейный коэффициент частичной корреляции между X и Y после удаления нелинейного эффекта Z равен 0,8844. Кроме того, обобщенный частный коэффициент корреляции между X и Z после устранения нелинейного эффекта Y составит 0,1581. Подробности смотрите в пакете R `generalCorr' и его описаниях. Моделирование и другие подробности приведены в книге Винод (2017) «Обобщенная корреляция и ядерная причинность с приложениями в экономике развития», Communications in Статистика – моделирование и вычисления, том. 46, [4513, 4534], доступно онлайн: 29 декабря 2015 г., URL https://doi.org/10.1080/03610918.2015.1122048 .

Использование рекурсивной формулы [ править ]

Решение задач линейной регрессии может оказаться дорогостоящим в вычислительном отношении. На самом деле, частная корреляция n -го порядка (т. е. с | Z | = n ) может быть легко вычислена из трех ( n - 1)-го порядка частных корреляций. Частная корреляция нулевого порядка ρ _{XY ·Ø} определяется как коэффициент регулярной корреляции ρ _XY .

Оно справедливо для любого $Z_{0}\in \mathbf {Z} ,$ что ^[3]

\rho _{XY\cdot \mathbf {Z} }={\frac {\rho _{XY\cdot \mathbf {Z} \setminus \{Z_{0}\}}-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}}\rho _{Z_{0}Y\cdot \mathbf {Z} \setminus \{Z_{0}\}}}{{\sqrt {1-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}}^{2}}}{\sqrt {1-\rho _{Z_{0}Y\cdot \mathbf {Z} \setminus \{Z_{0}\}}^{2}}}}}

Наивная реализация этого вычисления в виде рекурсивного алгоритма приводит к экспоненциальной временной сложности . Однако это вычисление имеет свойство перекрывающихся подзадач , например, использование динамического программирования или простое кэширование результатов рекурсивных вызовов приводит к сложности ${\mathcal {O}}(n^{3})$ .

Обратите внимание, что в случае, когда Z — одна переменная, это сводится к: ^{[ нужна ссылка ]}

\rho _{XY\cdot Z}={\frac {\rho _{XY}-\rho _{XZ}\rho _{ZY}}{{\sqrt {1-\rho _{XZ}^{2}}}{\sqrt {1-\rho _{ZY}^{2}}}}}

Использование обращения матрицы [ править ]

Частную корреляцию также можно записать через матрицу совместной точности. Рассмотрим набор случайных величин, $\mathbf {V} ={X_{1},\dots ,X_{n}}$ мощности n . Нам нужна частичная корреляция между двумя переменными $X_{i}$ и $X_{j}$ учитывая все остальные, т.е. $\mathbf {V} \setminus \{X_{i},X_{j}\}$ . Предположим, что (совместная/полная) ковариационная матрица $\Sigma =(\sigma _{ij})$ положительно определена и, следовательно, обратима . Если матрица точности определяется как $\Omega =(p_{ij})=\Sigma ^{-1}$ , затем

\rho _{X_{i}X_{j}\cdot \mathbf {V} \setminus \{X_{i},X_{j}\}}=-{\frac {p_{ij}}{\sqrt {p_{ii}p_{jj}}}}

( 1 )

Для расчета этого требуется $\Sigma ^{-1}$ , обратная ковариационной матрице $\Sigma$ который проходит в ${\mathcal {O}}(n^{3})$ время (с использованием выборочной ковариационной матрицы для получения выборочной частичной корреляции). Обратите внимание, что требуется только одна инверсия матрицы, чтобы получить все частные корреляции между парами переменных в $\mathbf {V}$ .

Чтобы доказать уравнение ( 1 ), вернитесь к предыдущим обозначениям (т.е. $X,Y,\mathbf {Z} \leftrightarrow X_{i},X_{j},\mathbf {V} \setminus \{X_{i},X_{j}\}$ начнем с определения частичной корреляции: ρ _{XY · Z} — это корреляция между остатками e _X и e _Y, возникающая в результате линейной регрессии X ) и с Z и Y с Z соответственно.

Во-первых, предположим $\beta ,\gamma$ – коэффициенты аппроксимации линейной регрессии; то есть,

\beta =\operatorname {argmin} _{\beta }\mathbb {E} \|X-\beta ^{T}Z\|^{2}

\gamma =\operatorname {argmin} _{\gamma }\mathbb {E} \|Y-\gamma ^{T}Z\|^{2}

Напишите совместную ковариационную матрицу для вектора $(X,Y,Z^{T})^{T}$ как

\Sigma ={\begin{bmatrix}\Sigma _{XX}&\Sigma _{XY}&\Sigma _{XZ}\\\Sigma _{YX}&\Sigma _{YY}&\Sigma _{YZ}\\\Sigma _{ZX}&\Sigma _{ZY}&\Sigma _{ZZ}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\\\end{bmatrix}}

где

C_{11}={\begin{bmatrix}\Sigma _{XX}&\Sigma _{XY}\\\Sigma _{YX}&\Sigma _{YY}\end{bmatrix}},\qquad C_{12}={\begin{bmatrix}\Sigma _{XZ}\\\Sigma _{YZ}\end{bmatrix}},\qquad C_{21}={\begin{bmatrix}\Sigma _{ZX}&\Sigma _{ZY}\end{bmatrix}},\qquad C_{22}=\Sigma _{ZZ}

Тогда стандартная формула линейной регрессии дает

\beta =\left(\Sigma _{ZZ}\right)^{-1}\Sigma _{ZX}

Следовательно, остатки можно записать как

R_{X}=X-\beta ^{T}Z=X-\Sigma _{XZ}\left(\Sigma _{ZZ}\right)^{-1}Z

Обратите внимание, что $R_{X}$ имеет нулевое ожидание из-за включения члена в $Z$ . Вычисление ковариации теперь дает

\operatorname {Cov} (R_{X},R_{Y})=\mathbb {E} (R_{X},R_{Y})=\dots =\Sigma _{XY}-\Sigma _{XZ}\left(\Sigma _{ZZ}\right)^{-1}\Sigma _{ZY}

( 2 )

Далее напишите матрицу точности $\Omega =\Sigma ^{-1}$ в аналогичной форме блока:

\Omega ={\begin{bmatrix}\Omega _{XX}&\Omega _{XY}&\Omega _{XZ}\\\Omega _{YX}&\Omega _{YY}&\Omega _{YZ}\\\Omega _{ZX}&\Omega _{ZY}&\Omega _{ZZ}\end{bmatrix}}={\begin{bmatrix}P_{11}&P_{12}\\P_{21}&P_{22}\\\end{bmatrix}}

Тогда по формуле Шура для обращения блочно-матрицы :

P_{11}^{-1}=C_{11}-C_{12}C_{22}^{-1}C_{21}

Элементы правой матрицы — это в точности ковариации, вычисленные ранее в ( 2 ), что дает

P_{11}^{-1}={\begin{bmatrix}\operatorname {Cov} (R_{X},R_{X})&\operatorname {Cov} (R_{X},R_{Y})\\\operatorname {Cov} (R_{Y},R_{X})&\operatorname {Cov} (R_{Y},R_{Y})\\\end{bmatrix}}

Использование формулы обратной матрицы 2×2 дает

{\begin{aligned}P_{11}^{-1}&={\frac {1}{{\text{det}}P_{11}}}{\begin{pmatrix}[P_{11}]_{22}&-[P_{11}]_{12}\\-[P_{11}]_{21}&[P_{11}]_{11}\\\end{pmatrix}}\\&={\frac {1}{{\text{det}}P_{11}}}{\begin{pmatrix}p_{YY}&-p_{XY}\\-p_{YX}&p_{XX}\\\end{pmatrix}}\end{aligned}}

Действительно, частичная корреляция

\rho _{XY\cdot Z}={\frac {\operatorname {Cov} (R_{X},R_{Y})}{\sqrt {\operatorname {Cov} (R_{X},R_{X})\operatorname {Cov} (R_{Y},R_{Y})}}}={\frac {-{\tfrac {1}{{\text{det}}P_{11}}}p_{XY}}{\sqrt {{\tfrac {1}{{\text{det}}P_{11}}}p_{XX}{\tfrac {1}{{\text{det}}P_{11}}}p_{YY}}}}=-{\frac {p_{XY}}{\sqrt {p_{XX}p_{YY}}}}

как заявлено в ( 1 ).

Интерпретация [ править ]

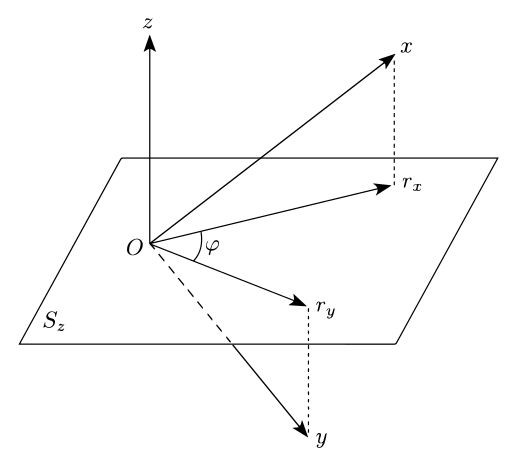
Геометрическая интерпретация частной корреляции для случая N = 3 наблюдений и, следовательно, двумерной гиперплоскости

Геометрический [ править ]

Пусть три переменные X , Y , Z (где Z «дополнительная переменная») выбраны из совместного распределения вероятностей по n переменным V. — «контрольная» или Далее, пусть v _i , 1 ≤ i ≤ N , будет N n -мерными наблюдениями iid , взятыми из совместного распределения вероятностей по V . Геометрическая интерпретация исходит из рассмотрения N -мерных векторов x (сформированных последовательными значениями X по наблюдениям), y (сформированных значениями Y ) и z (сформированных значениями Z ).

Можно показать, что остатки e _X,i, полученные в результате линейной регрессии X на Z , если их также рассматривать как N -мерный вектор e _X (обозначенный r _X на прилагаемом графике), имеют нулевое скалярное произведение с вектором z порожденный Z. , Это означает, что вектор невязок лежит на ( N –1) гиперплоскости S _z , перпендикулярной z -мерной .

То же самое относится и к остаткам e _Y,i, порождающим вектор e _Y . Тогда желаемая частная корреляция представляет собой φ между проекциями eX и eY _{перпендикулярную} x и _на y косинус соответственно z гиперплоскость, угла . ^[4]^{: гл. 7}

независимости условной Как тест

При предположении, что все задействованные переменные являются многомерными гауссовыми , частичная корреляция ρ _{XY · Z} равна нулю тогда и только тогда, когда условно от независима Y при заданном Z. X ^[1] Это свойство не выполняется в общем случае.

Чтобы проверить , является ли выборочная частичная корреляция ${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ означает, что истинная частичная корреляция популяции отличается от 0, z-преобразование Фишера частной корреляции можно использовать :

z({\hat {\rho }}_{XY\cdot \mathbf {Z} })={\frac {1}{2}}\ln \left({\frac {1+{\hat {\rho }}_{XY\cdot \mathbf {Z} }}{1-{\hat {\rho }}_{XY\cdot \mathbf {Z} }}}\right)

– Нулевая гипотеза это $H_{0}:\rho _{XY\cdot \mathbf {Z} }=0$ , для проверки на двустороннюю альтернативу $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ . $H_{0}$ можно отклонить, если

{\sqrt {N-|\mathbf {Z} |-3}}\cdot |z({\hat {\rho }}_{XY\cdot \mathbf {Z} })|>\Phi ^{-1}(1-\alpha /2)

где $\Phi$ — кумулятивная функция распределения гауссовского распределения с нулевым средним значением и единичным стандартным отклонением , $\alpha$ это значимости уровень $H_{0}$ , и $N$ это размер выборки . Это z -преобразование является приблизительным, и фактическое распределение выборочного (частного) коэффициента корреляции не является простым. Однако доступен точный t-критерий, основанный на сочетании коэффициента частичной регрессии, коэффициента частичной корреляции и частных дисперсий. ^[5]

Распределение выборочной частичной корреляции было описано Фишером. ^[6]

Получастичная корреляция (частичная корреляция) [ править ]

Статистика получастичной (или частичной) корреляции аналогична статистике частичной корреляции; оба сравнивают изменения двух переменных после учета определенных факторов. Однако для расчета получастичной корреляции необходимо сохранять третью переменную константой либо для X , либо для Y , но не для обоих; тогда как для частной корреляции третья переменная остается постоянной для обеих. ^[7] Получастичная корреляция сравнивает уникальную вариацию одной переменной (без удаления вариации, связанной с переменными Z )) с нефильтрованной вариацией другой, тогда как частичная корреляция сравнивает уникальную вариацию одной переменной с уникальной вариацией другой.

Получастичную корреляцию можно рассматривать как более уместную с практической точки зрения, «поскольку она масштабируется (т. е. относительно) общей изменчивости зависимой переменной (отклика)». ^[8] И наоборот, он менее полезен теоретически, поскольку менее точно определяет роль уникального вклада независимой переменной.

Абсолютное значение получастичной корреляции X с Y всегда меньше или равно абсолютному значению частичной корреляции X с Y . Причина в следующем: предположим, что корреляция X с Z удалена из X , что дает вектор остатка e _x . При вычислении получастичной корреляции Y по-прежнему содержит как уникальную дисперсию, так и дисперсию из-за ее связи Z. с Но ex _, , будучи некоррелированным с Z , может объяснить только некоторую уникальную часть дисперсии Y а не часть, связанную Z. с Напротив, при частичной корреляции необходимо объяснить только e _y (часть дисперсии Y , не связанную с Z меньше ), поэтому дисперсия того типа, которую ex _{не может объяснить ,} .

в анализе временных Использование рядов

При анализе временных рядов определяется частичная автокорреляционная функция (иногда «частичная корреляционная функция») временного ряда для задержки $h$ , как ^{[ нужна ссылка ]}

\varphi (h)=\rho _{X_{0}X_{h}\,\cdot \,\{X_{1},\,\dots \,,X_{h-1}\}}

Эта функция используется для определения подходящей длины задержки для авторегрессии .

См. также [ править ]

Ссылки [ править ]

^ Jump up to: Перейти обратно: ^а ^б Баба, Кунихиро; Ритуал Сибата; Масааки Сибуя (2004). «Частичная корреляция и условная корреляция как меры условной независимости». Статистический журнал Австралии и Новой Зеландии . 46 (4): 657–664. дои : 10.1111/j.1467-842X.2004.00360.x . S2CID 123130024 .
^ Гилфорд Дж. П., Фрухтер Б. (1973). Фундаментальная статистика в психологии и образовании . Токио: McGraw-Hill Kogakusha, LTD.
^ Ким, Сонхо (ноябрь 2015 г.). «ppcor: пакет R для быстрого расчета получастичных коэффициентов корреляции» . Коммуникации для статистических приложений и методов . 22 (6): 665–674. дои : 10.5351/CSAM.2015.22.6.665 . ISSN 2287-7843 . ПМЦ 4681537 . ПМИД 26688802 .
^ Раммель, Р.Дж. (1976). «Понимание корреляции» .
^ Кендалл М.Г., Стюарт А. (1973) Расширенная теория статистики , Том 2 (3-е издание), ISBN 0-85264-215-6 , раздел 27.22
^ Фишер, Р.А. (1924). «Распределение частного коэффициента корреляции» . Метрон . 3 (3–4): 329–332.
^ «Частичная и получастичная корреляция» . Архивировано из оригинала 6 февраля 2014 года.
^ StatSoft, Inc. (2010). «Получастичная (или частичная) корреляция» , Электронный учебник статистики. Талса, штат Оклахома: StatSoft, по состоянию на 15 января 2011 г.

Внешние ссылки [ править ]

Прохоров, А.В. (2001) [1994], «Частный коэффициент корреляции» , Энциклопедия математики , EMS Press
Математические формулы в разделе «Описание» процедуры PCORR числовой библиотеки IMSL.
Пример с тремя переменными

[Baba-1] Jump up to: Перейти обратно: ^а ^б Баба, Кунихиро; Ритуал Сибата; Масааки Сибуя (2004). «Частичная корреляция и условная корреляция как меры условной независимости». Статистический журнал Австралии и Новой Зеландии . 46 (4): 657–664. дои : 10.1111/j.1467-842X.2004.00360.x . S2CID 123130024 .

[2] Гилфорд Дж. П., Фрухтер Б. (1973). Фундаментальная статистика в психологии и образовании . Токио: McGraw-Hill Kogakusha, LTD.

[3] Ким, Сонхо (ноябрь 2015 г.). «ppcor: пакет R для быстрого расчета получастичных коэффициентов корреляции» . Коммуникации для статистических приложений и методов . 22 (6): 665–674. дои : 10.5351/CSAM.2015.22.6.665 . ISSN 2287-7843 . ПМЦ 4681537 . ПМИД 26688802 .

[4] Раммель, Р.Дж. (1976). «Понимание корреляции» .

[5] Кендалл М.Г., Стюарт А. (1973) Расширенная теория статистики , Том 2 (3-е издание), ISBN 0-85264-215-6 , раздел 27.22

[6] Фишер, Р.А. (1924). «Распределение частного коэффициента корреляции» . Метрон . 3 (3–4): 329–332.

[7] «Частичная и получастичная корреляция» . Архивировано из оригинала 6 февраля 2014 года.

[8] StatSoft, Inc. (2010). «Получастичная (или частичная) корреляция» , Электронный учебник статистики. Талса, штат Оклахома: StatSoft, по состоянию на 15 января 2011 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]